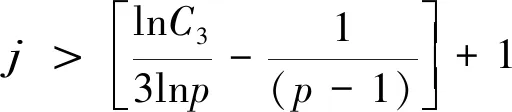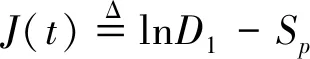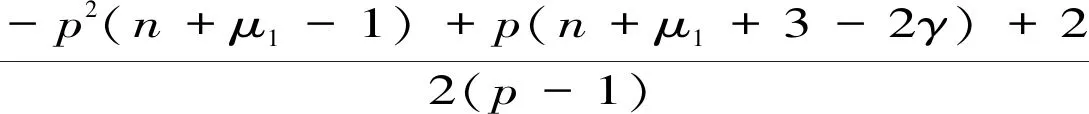一类带有记忆项的半线性波动方程解的爆破
曹德刚,陈雪丽,杨 晗
(西南交通大学 数学学院,成都 611756)
本文考虑一类带有记忆项的时间变系数耗散项与质量项的半线性波动方程的爆破问题
(1)
其中,常数μ1,μ2≥0,ε>0是小参数,Cγ=1/Γ(1-γ),γ∈(0,1),Γ(s)是Gamma函数。
近年来,在时间变系数的耗散项与质量项的半线性波动方程Cauchy问题
(2)
的研究中,关于整体解的存在性、衰减估计、解在有限时刻爆破和生命跨度估计的研究已有丰富的研究成果[1-5]。 对于带有记忆项的半线性波动方程
(3)
也有不少研究,如文献[6]研究了在问题(3)中取μ1=0时,利用迭代技巧与Slicing方法证明当1 时,解的整体性存在以及衰减估计,并利用试验函数法证明当 和n≥3,p∈(1,n/(n-2)],γ∈(0,(n-2)/n]时,解在有限时间爆破,但并未给出解的生命跨度估计。文献[8]研究了在问题(3)中取μ1>0,β=1时,对μ的取值作出以下分类考虑: 当μ=2,1 利用试验函数法证明问题(3)的解在有限时刻爆破,但未给出生命跨度估计。利用Kato引理证明当p≤n/(n-2)+,且1 其他相关研究见文献[9-10]。 下面根据文献[11],给出问题(1)的能量解的概念。 (4) 成立,则称u为问题(1)在[0,T)上的能量解。 引理1[4]假设u0,u1满足 (5) (6) 成立,其中C1=C1(p,u1,u0,R,φ)>0。 定理1当n≥1,δ≥0,p满足1 注1 当μ1=μ2=0时,定理1的结论可以与文献[6]定理1中解在有限时刻爆破与生命跨度估计上界的结论保持一致。 当μ1>0,μ2=0时,定理1的结论可以与文献[8]定理2.2中解在有限时刻爆破的结论保持一致。因此本文的结论是对文献[6,8]的推广。 由F(t)的定义可得 (7) 对(7)式关于t求微分,可得 (8) 考虑如下的代数方程 现将(8)式重新改为 (9) 在(9)式左右两侧同时乘以(1+t)y2+1,并在[0,t]上积分可得 对上式第一项用分部积分可得 (10) 在(10)式左右两侧再同时乘以(1+t)y1,并在[0,t]上分部积分可得 (11) 再由Hölder不等式,解的紧支集条件和有限传播速度可得 (12) 其中C0=meas(Bt+R)1-pR-n(p-1)>0。对∀t≥0,将(12)式带入(11)式,则有 (13) 接下来将获得F(t)的一个下界估计。 将引理1中(5)式带入(11)式中,则对于∀t>T0有 (14) 下面开始迭代讨论。 首先假设∀t>T0,j=1,2,3,…时,有 F(t)≥Dj(1+t)-aj(t-T0)bj, (15) 其中{Dj}j≥1,{aj}j≥1,{bj}j≥1>0。当j=1时,由(14)式知(15)式已经成立,其中 (16) 假设当j=k时,(15)式已经成立,下面将证明当j=k+1时,(15)式也成立。 结合(13)式和(15)式,对∀t>T0可得 (17) 在(17)式中令 (18) 因此(15)式对于j=k+1成立。结合(16)式和(18)式可得 (19) (20) lnDj≥plnDj-1+lnC3-3(j-1)lnp ≥p2lnDj-2+(1+p)lnC3-3(p(j-2)+(j-1))lnp ≥… (21) Dj≥e(pj-1(lnD1-Sp(∞))), (22) 将(19)(22)式带入(15)式中可得 (23) J(t)=lnD1-Sp(∞)-αln(1+t)+βln(t-T0) ≥lnD1-Sp(∞)-αln(2t-2T0)+βln(t-T0) ≥lnD1-Sp(∞)+(β-α)ln(t-T0)-αln2 ≥ln(D1(t-T0)β-α)-Sp(∞)-αln2, 而且有 因为pS(n+μ1,γ)是方程(n+μ1-1)p2-(n+μ1+3-2γ)p-2=0的正根,且p 定理1证明完毕。
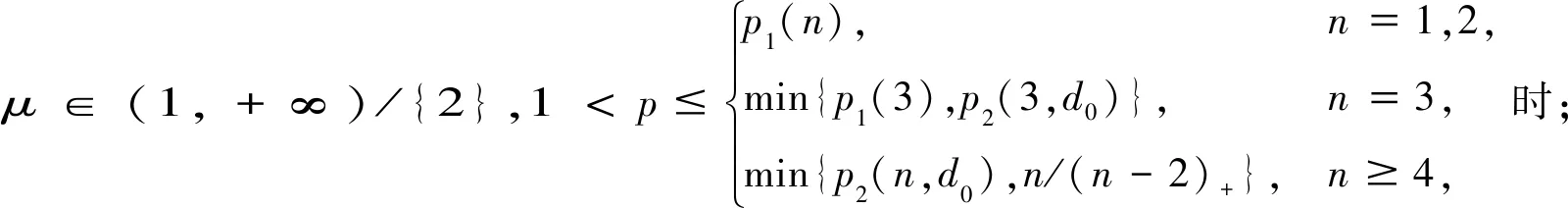
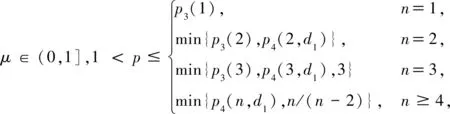

1 预备知识



2 主要结论

3 解的爆破与生命跨度估计