基于合成双射流的襟翼舵效增强技术研究

张鉴源，罗振兵,*，彭文强，梁睿琦，邓雄，王万波，赵志杰，刘杰夫

1.国防科技大学 空天科学学院，长沙 410073

2.中国空气动力研究与发展中心 低速空气动力研究所，绵阳 621000

0 引 言

飞机在执行各种大机动动作时，会处于大迎角状态，此时机翼和尾部水平/垂直安定面的背风面都存在大面积流动分离。当飞机需通过襟翼或升/降方向舵进行姿态控制时，舵面上的流动分离会使舵面所受气动力下降、舵面效率降低、舵面操纵能力不足，甚至还会使舵面反效。舵面效率低的根本原因是存在流动分离，如果对飞机采取舵效增强措施，有效控制舵面上的流动分离，使流动能附着在舵面表面，或者抑制流动分离的程度，减小分离区面积，便能改善舵面绕流情况。

主动流动控制已被证明可以减少甚至消除流动分离，从而提高机翼效率[1-7]。合成射流具有零质量流量特性，无需气源和管路，便于与机体集成化设计。通过合成射流激励器（SJA）[8-12]可以避免流动重新附着的不稳定性及不稳定空气动力载荷。气动表面形状的改变已经被证明有利于控制无人驾驶飞行器[11]和进气道[12]的分离。

合成射流激励器已被用于控制垂尾和襟翼的流动分离。Rathay 等采用合成射流在1∶25 垂尾缩比模型上进行风洞试验[13]，在无侧滑情况下，垂尾侧力增大了20%；同时在1∶19 垂尾缩比模型上进行了有侧滑的风洞试验[14]，侧力最大增大了34%；随后进一步增大模型尺度，在1∶9 模型上继续开展了风洞试验[15]，垂尾侧力最大增大了19%。Maines 等[16]在1∶4 薄翼战斗机缩比模型的后缘襟翼铰链处安装了合成射流激励器，进行了风洞试验，结果表明：在后缘襟翼铰链处施加流动控制影响了整个机翼上表面的压力分布；根据预估的升力增量和全尺寸合成射流激励器的性能，合成射流控制系统可以为战斗机额外提供1 500～1 600 lb（1 lb=0.453 592 37 kg）的升力。

随着研究的不断深入，合成射流技术的缺陷逐渐暴露。合成射流激励器存在环境适应性差和控制能力不足等问题，严重制约了其在高速流动控制中的应用[17]。针对这些局限，罗振兵等[17-20]设计了合成双射流激励器（DSJA），相较于合成射流激励器，合成双射流激励器的能量利用率提高了近1 倍，可控流场特征频率范围也提高了1 倍，大幅降低了振动膜振动引起的环境噪声，解决了合成射流技术环境适应性差和控制能力弱的问题。

王林[21]、李玉杰[22]分别通过数值模拟和试验证明：与传统的合成射流相比，合成双射流（DSJ）具有更好的控制效果；对于流动分离控制，合成双射流两出口在分离点之前或之间时有较强的控制效果。李玉杰等[23]通过风洞试验证明：合成双射流对机翼大迎角流动分离具有较强的控制能力，可显著提高机翼流动分离迎角；出口位置越靠近分离点，控制效果越明显；合成双射流激励器射流能量越高，控制机翼流动分离的能力越好。

基于合成双射流激励器的优越性能，本文对二维简单襟翼展开研究，利用数值模拟探究阵列式合成双射流对二维简单襟翼气动性能的影响，以及不同参数的控制效果；并在此基础上开展飞行试验，验证阵列式合成双射流对简单襟翼表面流动分离的控制能力。

1 数值模型与计算方法

1.1 合成双射流控制参数

DSJ 的控制参数包括无量纲驱动频率F+和无量纲动量系数Cµ，其表达式如下：

式中：f为驱动频率，u∞为来流速度，uj为射流峰值速度，c1为襟翼弦长，d为射流出口宽度，ρj为射流密度，ρ∞为来流密度。

1.2 数值模型

选用NACA2412 二维翼型作为控制对象，如图1（a）所示，翼型弦长c=0.5 m，襟翼弦长c1=0.135 m，翼型最大厚度h=0.06 m，舵面偏转角度为36°。在襟翼上共设置了5 个合成双射流激励器，分别位于0%、4%、28%、52.4%和72%襟翼弦长处，如图1（b）所示。第1 个DSJA 腔体长2%c、高8%h，出口1 与上表面切向成 70°、宽度为0.18%c，出口2 方向平行于弦长指向流向、宽度为0.4%c，如图1（c）所示。其余4 个DSJA 腔体每个长2%c、高3%h，出口长度为0.57%c、宽度为0.18%c、与上表面切向成30°，如图1（d）所示。

图1 翼型及DSJA 布置方案和结构示意图Fig.1 Scheme of airfoil and DSJA layout

1.3 数值模拟方法

数值模型计算域为O 型网格拓扑结构，其计算域及表面网格如图2 所示。翼型表面和射流口位置的网格进行了加密处理，第一层网格高y+≈1，网格总数为8.148 5 × 104。翼型表面和激励器壁面设为无滑移壁面边界条件，计算域外边界设为压力远场条件。DSJA 振动膜的压力入口条件设置为周期性波动，能较好地模拟出膜片振动带来的吹吸效应，其数学表达式为：

图2 计算网格示意图Fig.2 Diagram of computing grid

式中：p0为激励器出口当地静压，pv为膜片振动所产生的动压，pv=(0.5ρjujsin 2πft)。此外，空气为理想气体，使用Sutherland 公式计算气体黏性。

选择有限体积法离散二维可压非定常雷诺平均Navier-Stokes 方程，利用基于密度的求解器进行求解。因为流动中伴随流动分离现象，所以湍流模型选用SST k-ω模型。采用Roe-FDS 通量差分分裂格式对空间项进行离散，对流项采用一阶迎风格式，时间离散格式为一阶隐式格式。温度设置为300 K，大气压强为101 325 Pa，来流马赫数Ma=0.1。在非定常计算中，设置时间步长为激励器驱动周期的1/40，共进行50 个流动控制周期的计算，以确保合成双射流能产生稳定的周期性流场。

针对NACA0015 翼型，采用上述方法进行数值模拟，并与文献中的试验结果[24-25]进行对比，试验结果如图3 所示，其中，CL为升力系数，CD为阻力系数，α为迎角。结果表明：该数值模拟方法可以较好地预测升力系数、阻力系数及失速迎角，具有一定的合理性。

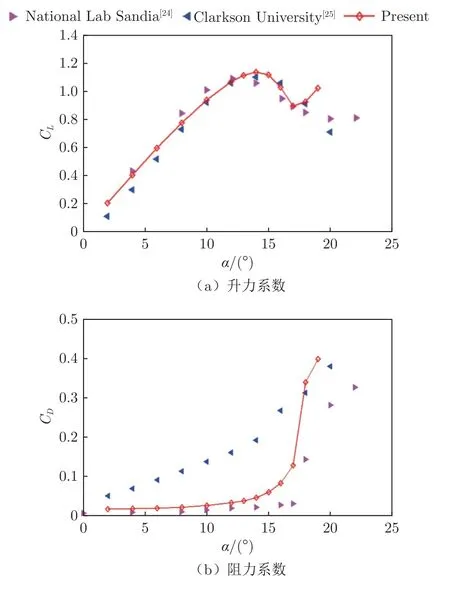
图3 升力系数、阻力系数的数值模拟与试验结果对比Fig.3 Comparison between numerical simulation and test results of lift coefficient and drag coefficient

针对简单襟翼数值模型，采用不同数量的网格进行了数值模拟，试验结果如表1 所示。由表可见：当网格量大于80 000 时，升、阻力系数趋于稳定，故本研究采用80 000 量级的网格进行计算。

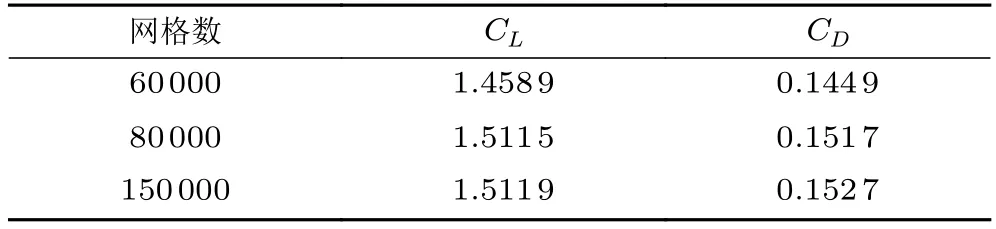
表1 不同网格下的升、阻力系数Table 1 Lift and drag coefficients with different number of grids

2 气动力控制特性

2.1 驱动频率参数影响

在保证无量纲动量系数Cµ=2.695×10-3不变的情况下，在0°～8°迎角范围内对襟翼施加不同驱动频率（F+为0.49、0.97、1.95、3.89）的控制，其升力系数、阻力系数、力矩系数CM、升阻比L/D 变化如图4 所示。

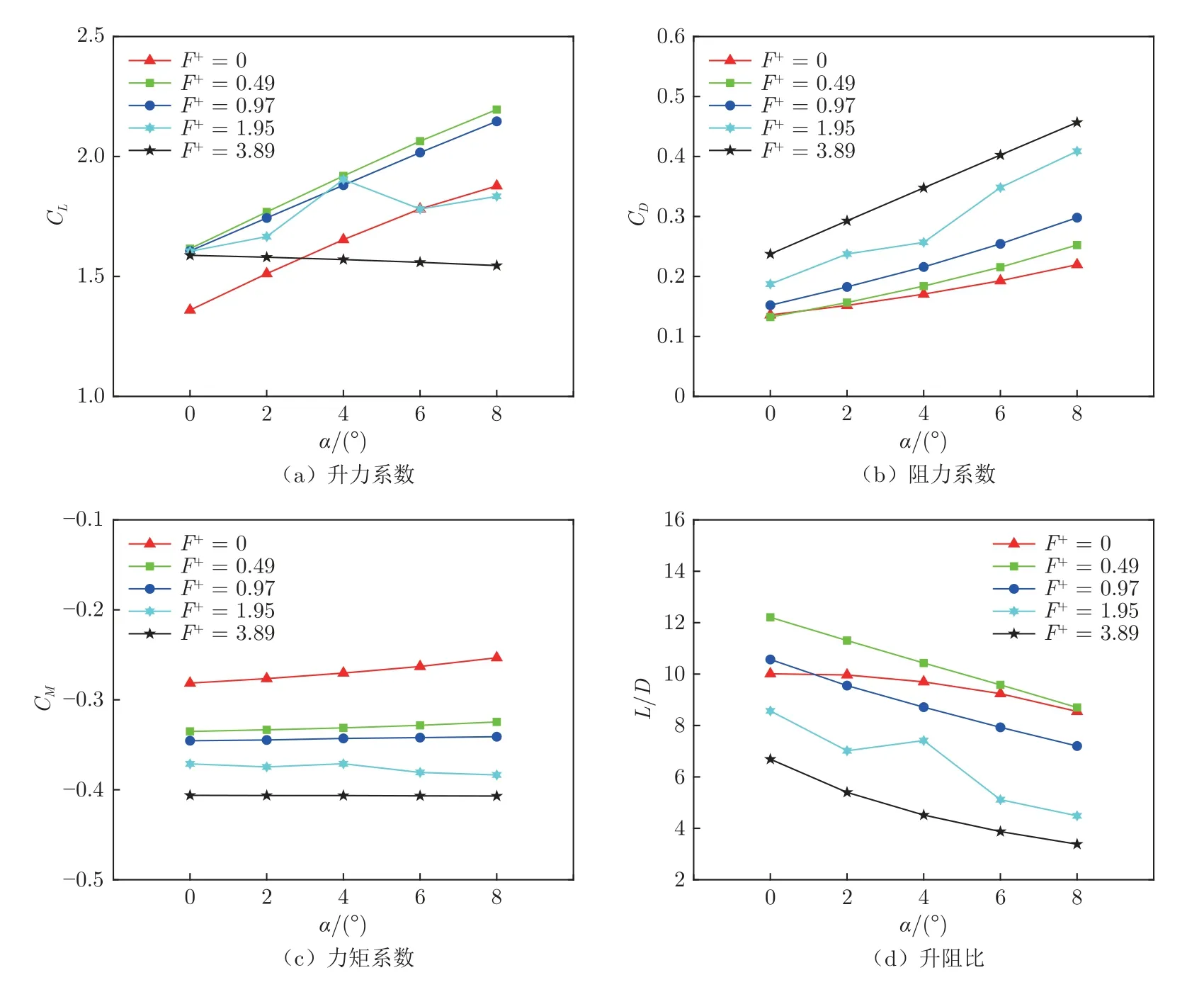
图4 不同驱动频率控制气动系数对比Fig.4 Comparison of aerodynamic coefficients of different driving frequencies

从图4（a）可以看出：在施加0.49 倍和0.97 倍特征频率的控制后，相同迎角下的升力系数较无控制情况有明显提升，且随迎角增大而线性增加；施加1.95 倍特征频率的控制时，在4°迎角时升力系数陡增，随着迎角进一步增大，升力系数突然降低，甚至低于无控制状态，整体呈非线性变化趋势；当驱动频率增加到3.89 倍特征频率后，随着迎角增大，升力系数始终缓慢降低，呈线性变化趋势，迎角增大到4°以上后，升力系数低于无控制状态。从图4（b）和（c）可以看出：施加控制后，阻力系数和力矩系数较无控制情况下有所增大，且随驱动频率的升高而增大，二者均呈现出较好的线性关系。值得注意的是，在同一驱动频率下，力矩系数随迎角的变化并不明显。从图4（d）可以看出：随着迎角增大，升阻比整体呈下降趋势；在施加0.49 倍的特征频率控制后，各个迎角下的升阻比较无控制状态均有所提升；施加0.97 倍的特征频率控制后，除0°迎角时升阻比有所提升，其余迎角下升阻比均低于无控制状态。

从上述控制特性可知，DSJ 对襟翼的控制在小迎角下可以达到增加升力、增强舵效的效果，且高频射流对舵效的增强效果更好，而0.49 倍的特征频率控制对升阻比的提升效果最好。

2.2 动量系数参数影响

在保证无量纲驱动频率F+=0.97不变的情况下，在0°～8°迎角范围内对襟翼施加不同动量系数（Cµ为2.065 × 10-3、2.695 × 10-3、3.01 × 10-3）的控制，其升力系数、阻力系数、力矩系数、升阻比变化如图5 所示。

从图5（a）来看，随着动量系数增大，升力系数线性增加，与不施加控制情况相比显著提高。从图5（b）来看，阻力系数随迎角增大线性增大，与不施加控制情况相比明显增大，但不同动量系数的结果差别并不明显。图5（c）来看，力矩系数也随动量系数增大而增大，与不施加控制情况相比显著提高，且与驱动频率的影响类似，同一动量系数下，力矩系数随迎角的变化并不明显。从图5（d）来看，只有在0°迎角、Cµ为2.695 × 10-3和3.01 × 10-3时，升阻比才较无控制情况有所提高，其余工况下升阻比均低于不施加控制情况。

从上述控制特性可知，在不考虑升阻比的条件下，在一定范围内动量系数越高，DSJ 对该翼型气动性能的综合提升越高。

3 流场控制机理

以0°～8°迎角下不同DSJ 控制参数为例，分析控制前后机翼流场、表面压力分布，探究襟翼合成双射流对该试验翼型的流动控制机理。

图6 为机翼在迎角为4°时，DSJ 不工作、在最佳频率工作和在最佳动量系数下工作时的速度云图，图中X、Y 轴代表流场的坐标位置，其零点位于翼型前缘处。无控制时，4°迎角下的无控流场如图6（a）所示：机翼上表面发生流动分离（ls/c=0.78，ls为分离点X 轴坐标），襟翼上方形成了一个大分离区。F+=3.89、Cµ=2.695×10-3时，DSJ 的舵效增强效果最好，其受控流场如图6（b）所示。由图可见：襟翼上表面大部分流动分离被抑制，流动分离点后移至ls/c=0.93处，流线基本再附，控制效果明显。F+=0.97、Cµ=3.010×10-3时，DSJ以最大动量系数状态工作，其受控流场如图6（c）所示。与图6（b）类似，此时襟翼上表面大部分流动分离被抑制，流动分离点后移至ls/c=0.95处，流线基本再附。

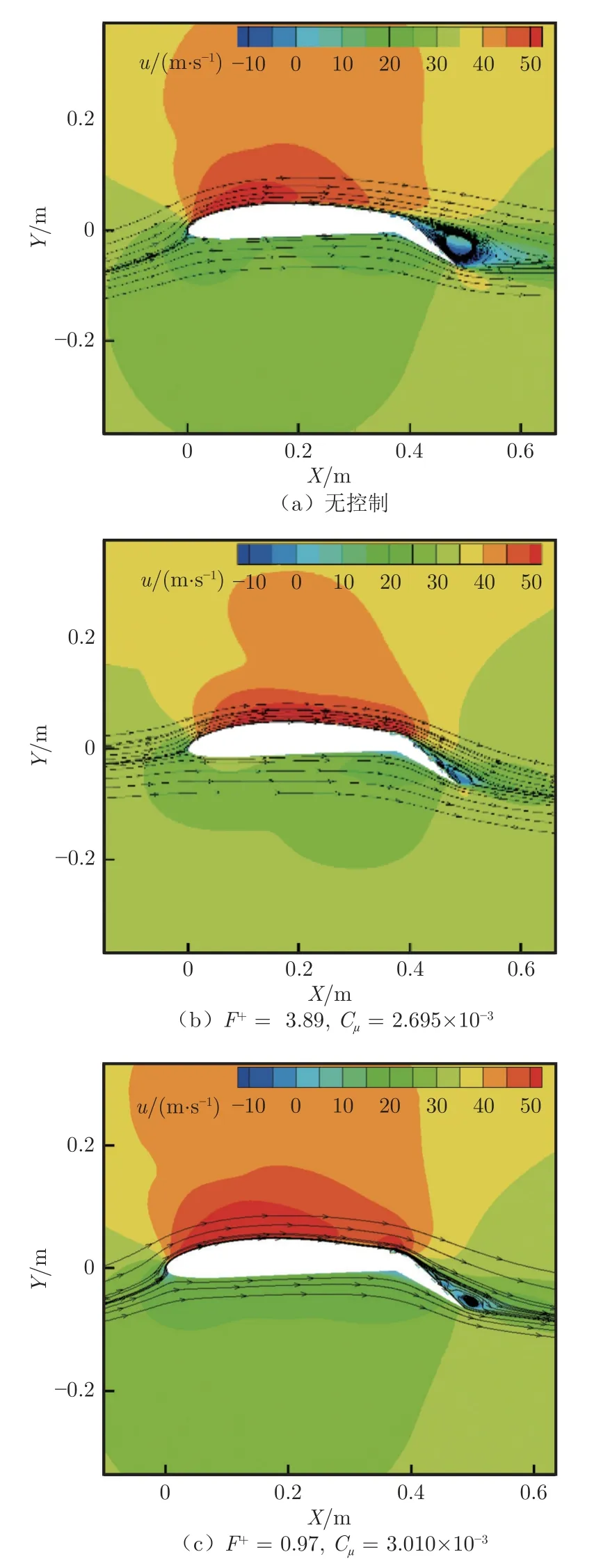
图6 不同控制参数的速度云图（α=4°）Fig.6 Velocity diagram of different control parameters (α=4°)

从图6 可以看出：无控制时，襟翼上表面流场从襟翼铰链处开始分离，襟翼的上翼面完全被回流区包围。施加控制后，由于DSJ 的周期性吹/吸气作用，边界层出现了小尺度的涡结构，非定常射流产生的周期性湍流涡结构增强了边界层的动量交换，改善了上翼面的流场质量。

6°迎角、Cµ=2.065×10-3、F+分别为0.97、3.89的流场速度云图与翼型表面压力系数Cp分布对比如图7 所示。从图7（a）和（b）可以看出：施加控制后，不论驱动频率高低，襟翼上表面的分离区都得到有效控制，虽然在襟翼后方仍存在一部分分离区，但表面边界层流线仍完全再附，流动情况明显改善；驱动频率增大后，机翼上表面高流速区域面积减小；DSJ 形成的周期性涡结构与襟翼上表面分离区相互融合，增强了外流与边界层内的流动掺混；周期性交替吹/吸将吸走襟翼表面低流速的边界层，并为边界层注入能量，将分离区外的高速气流引射至分离区内，提高了襟翼表面边界层流动速度，从而抑制分离，减小了分离区面积。从图7（c）来看：驱动频率增大后，前缘驻点上移，机翼前缘压力包络面积显著减小，襟翼上表面分离区吸力峰值变化不明显。

图7 不同频率下的速度云图及压力系数分布（α=6°）Fig.7 Velocity nephogram and pressure coefficient distribution at different frequencies (α=6°)

从以上结果可以看出，在一定范围内，DSJ 高频控制效果比低频更明显，增强舵效的效果更好。

4°迎角、F+=0.97、Cµ分别为2.065 × 10-3和3.010 × 10-3时的流场特征和压力分布对比如图8 所示。从图8（a）和（b）看，动量系数越高，对襟翼上方流动分离的抑制效果越明显，分离点更延后，周期性涡结构与分离区融合程度更深，外流与边界层内的流动掺混更强，影响范围更大，对分离流场的控制能力更强。从图8（c）看，施加控制后，动量系数改变对机翼前缘压力几乎没有影响；随着动量系数的增大，合成双射流涡结构穿透能力更强，对分离区抑制效果更好；襟翼上方吸力峰值随动量系数增大大幅上升，翼型整体升力增大，力矩系数增大。从以上结果可以看出，在一定范围内，高动量系数的DSJ 对流场的控制能力更强。

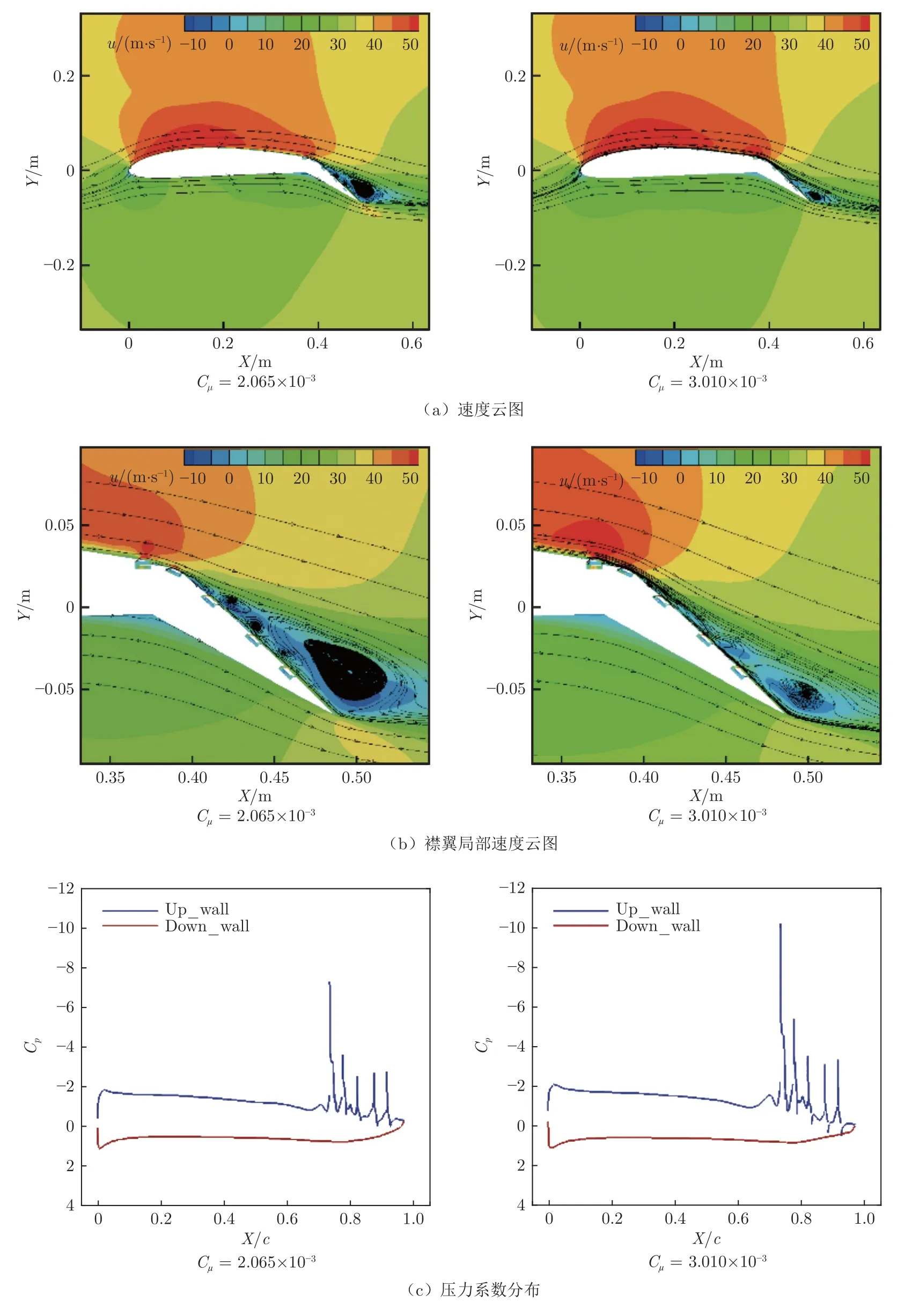
图8 不同动量系数下的速度云图及压力系数分布（α=4°）Fig.8 Velocity nephogram and pressure coefficient distribution at different momentum coefficient (α=4°)

4 飞行试验研究

开展飞行试验研究得到在飞行试验层面的控制结果，以验证阵列合成双射流舵效增强技术的可行性。

4.1 激励器模型及飞行平台

如图9 所示，对传统合成双射流激励器结构进行改进，设计了双膜三腔与单膜双腔混合式合成双射流激励器。射流出口宽度为1 mm，出口指向y 轴正向，襟翼偏角为35°，x、y、z 方向上的长度分别为65、103 和40 mm，整个激励器尺寸很小，极易实现一体化设计。

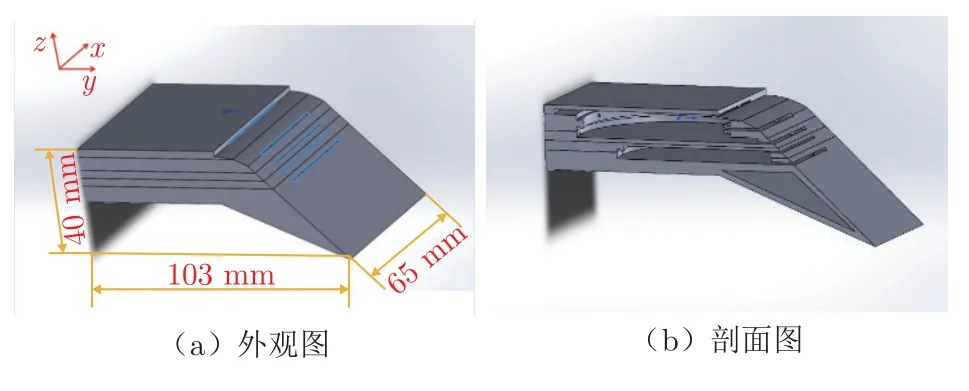
图9 阵列合成双射流激励器模型Fig.9 The model of array dual synthetic jet actuator

无人机和激励器安装位置如图10 所示。该无人机结构简单，运行成本较低，且机翼满足激励器安装所需空间，同时具有姿态角控制系统，有副翼可用于控制滚转、升降舵用于控制俯仰，满足飞行试验所需设备条件。

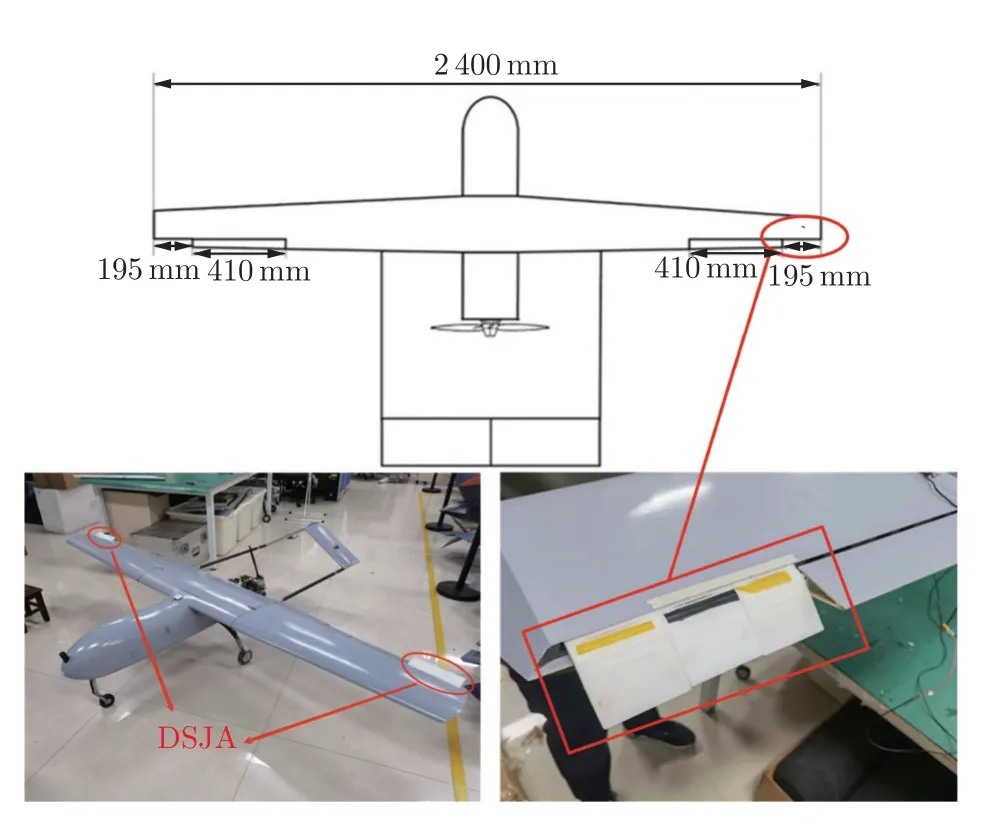
图10 无人机示意图和DSJA 安装位置示意图Fig.10 Size of flight platform and DSJA installation position

飞机总体气动布局为上单翼，尾翼为倒V 尾。装配总质量为15 kg，展长为2 400 mm，机翼面积为0.732 m2；前缘后掠角为4.1°，翼根弦长为370 mm，翼尖弦长为240 mm，副翼长度为410 mm；飞行速度为25 m/s。在机翼翼梢尾端布置反向安装合成双射流激励器，对机翼产生减升增阻的效果，布置长度为195 mm。

4.2 飞行试验结果分析

飞行试验中，当飞行器处于平飞状态（迎角为2°～4°）时，同一时间仅开启一侧DSJA，以实现单方向的滚转姿态操控，激励器驱动电压为 ± 240 V、驱动频率为600 Hz。共进行2 个架次的测试，其中第一架次测试仅开启左侧DSJA，第二架次测试仅开启右侧DSJA。

左侧DSJA开启前、后的飞行状态机上视角如图11 所示。从图中可以发现：在施加控制3 s 后，飞行器姿态明显发生变化，这是因为在左侧DSJA 控制下，飞行器左侧机翼升力减小、阻力增大，飞行器受到向左的滚转力矩和向左的偏航力矩，2 个力矩耦合使飞行器向左侧滚转偏航。控制过程中的飞行姿态参数变化如图12 所示。在施控前，飞手将飞机调控至近似平飞状态，在A 点处，飞手松杆，并开启DSJA 控制，B 点处机械舵面介入控制，DSJA 控制结束。从图中可以发现：左侧DSJA 开启瞬间产生了幅值较小的右滚转角速度，随后滚转角速度反向并不断增大，最大滚转角速度可达11.75 (°)/s；左侧DSJA完全开启后会产生持续约1 s 的幅值较小的右偏航角速度，这可能是由空中侧风所致，随后偏航角反向并不断增大。在二者的共同作用下，飞行器向左发生滚转，且滚转角不断增大，同时向左发生偏航，滚转、偏航角速度的变化几乎没有延迟。

图11 左侧DSJA 控制效果Fig.11 Control effect of left DSJA

图12 施加左侧DSJA 控制后的飞行参数Fig.12 Flight parameters after applying left DSJA control

右侧DSJA 开启前、后的飞行状态机上视角如图13 所示。从图中可以发现：在施加控制3 s 后，飞行器姿态明显发生变化，这是因为在右侧DSJA 控制下，飞行器右侧机翼升力减小、阻力增大，飞行器受到向右的滚转力矩和向右的偏航力矩，2 个力矩耦合后使飞行器向右侧滚转偏航。控制过程中的飞行姿态参数变化如图14 所示。从图中可以发现：右侧DSJA 开启瞬间产生了幅值较小的右滚转角速度，且不断增大，最大滚转角速度可达15.91 (°)/s；同时产生右偏航角速度，且不断增大。在二者的综合作用下，飞行器向右发生滚转，且滚转角不断增大，同时向右发生偏航。滚转、偏航角速度的变化几乎没有延迟，滚转角的变化存在约0.3 s 的延迟。

图13 右侧DSJA 控制效果Fig.13 Control effect of right DSJA

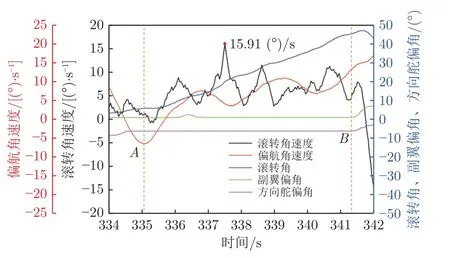
图14 施加右侧DSJA 控制后的飞行参数变化Fig.14 Flight parameters after applying right DSJA control

通过上述飞行参数对比，还可以明显发现左、右侧DSJA 控制都会产生一定的角速度波动。一方面，这是由于合成双射流操控时间过短，飞行器姿态参数还未稳定，波动较大；另一方面，是由于合成双射流操控力矩、飞行器自身稳定力矩、空中侧风的综合作用。

5 总 结

本文数值模拟了在NACA2412 翼型襟翼上表面设置5 个合成双射流激励器时，控制参数对该翼型气动特性的影响，揭示了控制机理；并对DSJA 与襟翼进行了一体化设计，将DSJA 安装在常规布局无人机上，进行了飞行试验验证，具体结论如下：

1） 无DSJ 控制时，随迎角增大，舵率降低、升力增大、阻力增大、升阻比降低。

2） 施加DSJ 控制，可在襟翼上方形成周期性涡结构，加强边界层内低速流体与主流的掺混，增大边界层的能量，抑制分离，显著提高舵效，并提高了襟翼上表面流动速度，从而增大升力；高频条件下，翼型前缘驻点前移，翼型失速迎角变大；不考虑升阻比，在一定范围内，高动量系数的合成双射流增大升力、增强舵效的效果更好。

3） 飞行试验结果显示：DSJA 工作时，襟翼舵效得到显著增强，产生的减升增阻效果实现了无人机的滚转与偏航，两力矩耦合使飞机向同一方向滚转偏航，验证了DSJA 在舵效增强方面的可行性与控制效果。