贴壁二维方柱绕流对壁面摩擦应力的影响

张之豪，傅奇星，王庆洋，徐胜金,*

1.清华大学 航天航空学院，北京 100084 2.中国航天空气动力技术研究院，北京 100074 3.中国汽车工程研究院股份有限公司，重庆 401122

0 引 言

二维方柱绕流问题是典型的分离流问题，在工程中应用广泛。自由平行来流绕零迎角方柱运动时，根据雷诺数的不同，可能在第一个迎流的棱角处产生分离，出现再附后还可能在尾流附近的棱角处再次分离。在全局不稳定性和局部不稳定性机制作用下，方柱上下分离的自由剪切层会绕曲形成交替出现的大尺度涡，并在方柱下游产生一定宽度的尾流区[1-2]。在方柱后缘布置分离板[3-4]，可以抑制上下自由剪切层的绕曲，在近尾流区不会形成交替出现的大尺度涡。

当二维方柱置于平板边界层内时（如广泛存在于建筑、桥梁、燃气轮机叶片冷却、海底管道输运等工程应用中的贴壁方柱绕流），来流速度呈梯度分布，因平板的存在，流动只会在方柱上表面出现分离，形成含有涡量的大尺度流动结构[5-8]。平板的存在，相当于将无限长的分离板置于方柱下方，不仅使方柱下表面无法产生分离流，也会对上表面的分离流产生影响。Panigrahi 和Acharya[9-10]采用热线与激光多普勒测速技术（LDV）研究了不同雷诺数下的方柱下游流动速度功率谱及特征频率，发现大尺度流动结构的脱落频率与雷诺数呈线性关系，并指出剪切层的Kelvin-Helmholtz 不稳定性模式与后台阶流动类似。通过模式识别提取了涡旋运动的随机部分与相干部分，发现剪切层外缘的流动由涡旋诱导的大尺度上抛运动所主导，这种上抛运动与流动速度的非高斯分布形式存在重要关联。流动绕过方柱后产生2 个差异明显的区域[11]：一为分离/回流区，一为恢复/重建区。分离/回流区是指从方柱前缘流动分离点至下游平板流动再附点之间的区域，该区域内存在狭长的回流泡，是流动结构生成、发展的主要区域，流动具有较强的间歇性；恢复/重建区位于流动再附点下游区域，该区域内流动结构逐渐耗散，流场逐渐恢复为湍流边界层。进一步研究发现，在Kelvin-Helmholtz 不稳定性作用下，方柱剪切层产生低频振荡，在方柱上表面形成大尺度流动结构，并类似涡脱一样产生流动分离[12]。Shi 等[13]采用时间分辨粒子图像测速技术（TR-PIV）对方柱下游流场进行了研究，分析了大尺度流动结构对流场非定常特性的影响，发现大尺度再附涡与低频振荡分离泡之间存在相互作用，导致再附点附近流动间歇性因子发生急剧变化。

本文就贴壁二维方柱绕流对下游壁面摩擦应力的影响机制开展实验研究，以期为深入理解表面冲蚀、污染物聚集、近壁面湍流耗散等问题的机理提供参考。

1 实验方案

实验在低速直流风洞（实验段长、宽、高尺寸为2 m × 0.5 m × 0.5 m）中进行。如图1 所示，在距风洞底壁0.16 m 处水平放置光滑平板。平板前缘为楔形，在距前缘20 mm 处放置直径5 mm 的绊线，以促进边界层转捩，获得充分发展的湍流边界层。平板后缘安装角度可调节的尾板，实验时可通过调节尾板角度使平板边界层沿流向满足零压梯度条件。贴壁二维方柱置于距平板前缘1 m 处，方柱宽度D=10 mm，展长0.5 m，与风洞实验段截面宽度一致。来流风速U0=15 m/s，基于方柱宽度D 和来流风速U0定义的雷诺数ReD=1.1 × 104。经热线测量，来流湍流度为0.3%。

图1 平板及贴壁二维方柱示意图Fig.1 Diagram of flat plate and wall mounted 2D square cylinder

无方柱情况下，经边界层热线测量，以方柱所在位置边界层动量厚度θ（根据流向平均速度剖面积分得到）定义的雷诺数为Reθ=U0θ/ν=5 270（空气的运动黏性系数ν=1.51 × 10-5m2/s）。边界层热线单点采样频率20 kHz，采样时间10 s。

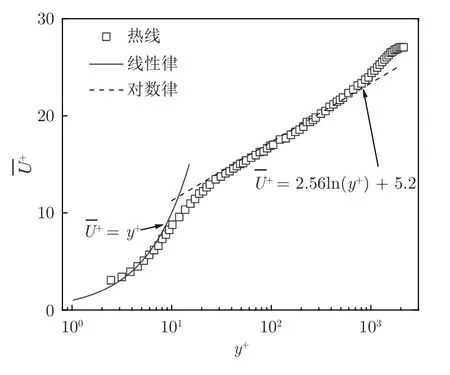
图2 平板湍流边界层流向平均速度剖面Fig.2 Profile of time-averaged streamwise velocity of flat plate TBL

1.1 流场测量

使用2D2C TR-PIV 测速系统对贴壁二维方柱下游流场进行测量。测速系统包括高速相机（分辨率1 280 像素×800 像素，配备最大光圈3.5、180 mm微距镜头）、Nd-YAG 激光器（波长532 nm，最大能量40 mJ，频率10～10 000 Hz）、BNC 575 同步控制器。选用经Laskin 喷嘴雾化的癸二酸二辛脂（DEHS）烟雾颗粒（直径2 µm）作为示踪粒子，在直流风洞入口处释放，经充分混合后进入风洞实验段。图3 为流场测量示意图。

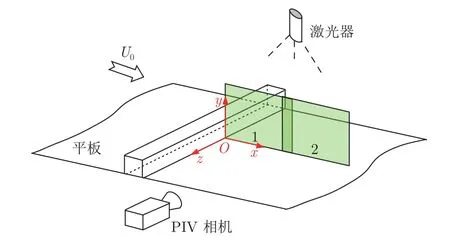
图3 贴壁二维方柱下游流场PIV 测量示意图Fig.3 Diagram of PIV measurement of flow field downstream of the 2D wall-mounted square cylinder

如图3 所示，为在同等像素分辨率下获得更为精细的流场结构，缩小拍摄视场，沿流向（x 向）分2 个区域进行测量。区域1 和2 的法向（y 向）视场范围均为0 < y/D < 4，流向视场范围分别为0 < x/D <8、6 < x/D < 14。2 个区域有宽为2D 的重叠区域，以便在进行数据统计平均时拼接测量区域。PIV 使用双帧双曝光工作模式，采样频率为1 kHz，2 个区域均采集8 000 对图像，2 帧图像时间间隔为50 µs。

1.2 壁面动态摩擦应力测量

热线能够获得精准的动态速度信息，但常规单丝热线在近壁面应用时会面临壁面干扰、无法靠近壁面、无法判断动态速度方向等困难。本文研发了平行双丝热线传感器，结合基于机器视觉的高精度定位系统，实现壁面动态摩擦应力测量。

摩擦应力测量原理如图4 所示。热线探头尖端装有2 根平行热丝（直径5 µm、法向间距0.025 mm、流向间距0.6 mm）。测量时，将平行双丝热线（热线1、热线2）伸入至黏性底层，热线探杆垂直于壁面，2 根热线与壁面平行、与来流方向垂直。根据2 根热线测点的流速U1(t)、U2(t)及热线与壁面的距离h1、h2，由牛顿内摩擦定律可得到2 根热线所对应的壁面动态摩擦应力τ1(t)、τ2(t)。

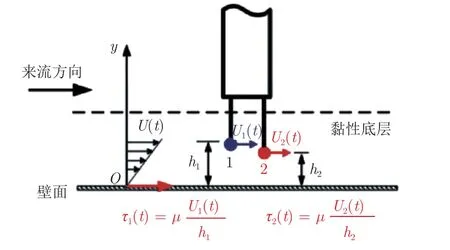
图4 摩擦应力测量原理示意图Fig.4 Principle of wall shear stress measurement

热线1 和2 的流向位置不同，上游热线和连接热线的支架对流动有阻碍作用，使得下游热线处的流速略低于上游热线。当近壁区域流动方向改变时，2 根热线测点处的流速差异也会发生改变。流速变化体现为热线输出电压的变化，因此，可根据2 根热线输出电压差的大小，判断壁面动态摩擦应力的方向。图5 给出了动态摩擦应力方向判别的具体方法。设定热线1 位于上游，摩擦应力与主流来流方向相同时为正，即τ(t) > 0；与主流来流方向相反时（回流方向）为负，即τ(t) < 0。测量时，同步获得2 根热线的电压信号E1(t)和E2(t)。在判断ti时刻的摩擦应力方向时，为增强鲁棒性，计算ti时刻附近时间段[ti- ts,ti+ ts]内电压差的平均值=与判断阈值ΔEth进行比较：若>∆Eth，则τ(ti) > 0；若<∆Eth，则τ(ti) < 0。由于下游热线处的流动受到上游热线及支架的干扰，为提高测量精度，无论动态摩擦应力方向如何，均使用上游热线的摩擦应力测量值作为当前时刻的摩擦应力，即：若τ(ti) > 0，τ(ti)=τ1(ti)；若τ(ti) < 0，则τ(ti)=-τ2(ti)。

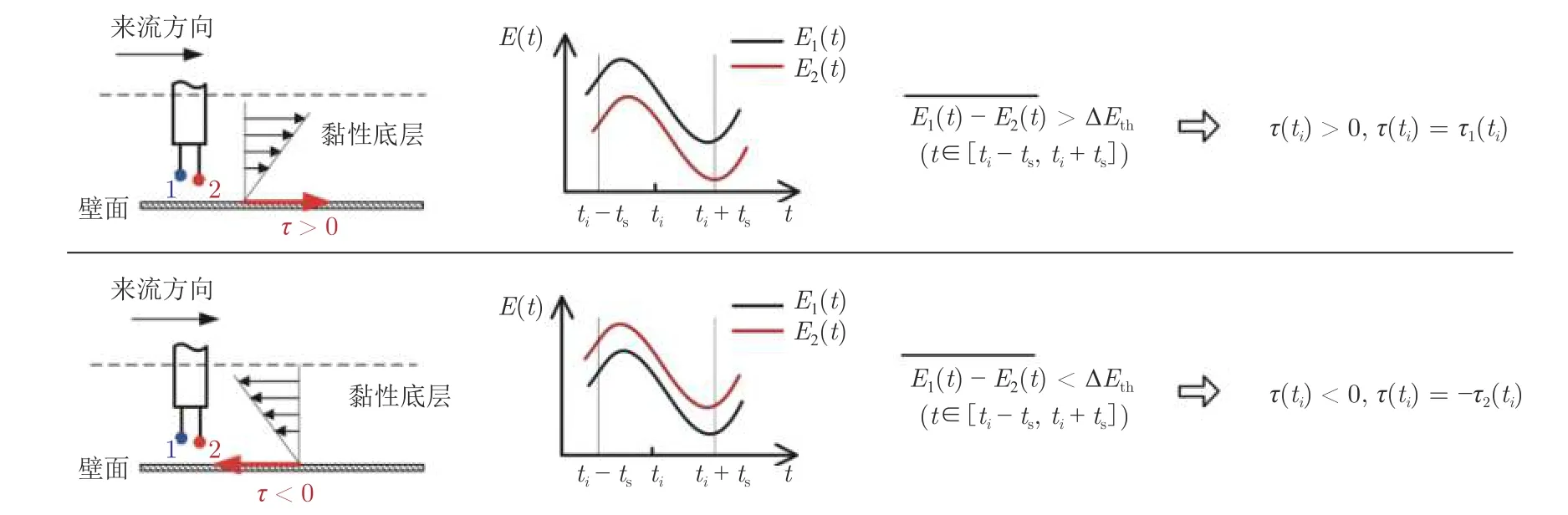
图5 动态摩擦应力方向判断示意图Fig.5 Diagram of dynamic shear stress direction judgment

根据牛顿内摩擦定律，壁面摩擦应力与热线测点处流速存在对应关系，可直接标定热线电压与摩擦应力之间的函数关系。标定时的热线位置与测量位置相同，尽量确保壁面影响一致，将壁面影响包含在标定曲线中。利用基于图像识别的精密定位系统，将热线定位至湍流边界层黏性底层内。本文平板镜像效果良好，可根据热线图像及热线在平板上的镜像确定热线与壁面之间的距离，定位精度约4.2 µm。本文将2 根热线定位至距壁面h1=0.1 mm和h2=0.075 mm 处，在无方柱情况下Reθ=5 270的湍流边界层中分别对应y1+=4.5、y2+=3.3，确保2 根热线处于黏性底层内。

为减小热线和支架的流动干扰导致的标定误差，分别将热线1 和2 置于上游进行标定。标定时，将平行双丝热线传感器置于距平板（如图1 所示，但无绊线）前缘水平距离55 mm 处，利用平板层流边界层已知的壁面摩擦应力对平行双丝热线进行标定。层流边界层的壁面摩擦应力根据Blasius 解计算得到，标定时的来流风速U0=0 m/s 及U0=3～18 m/s（间隔1 m/s），对应平均摩擦应力标定范围为0～0.51 Pa。标定结果如图6 所示。

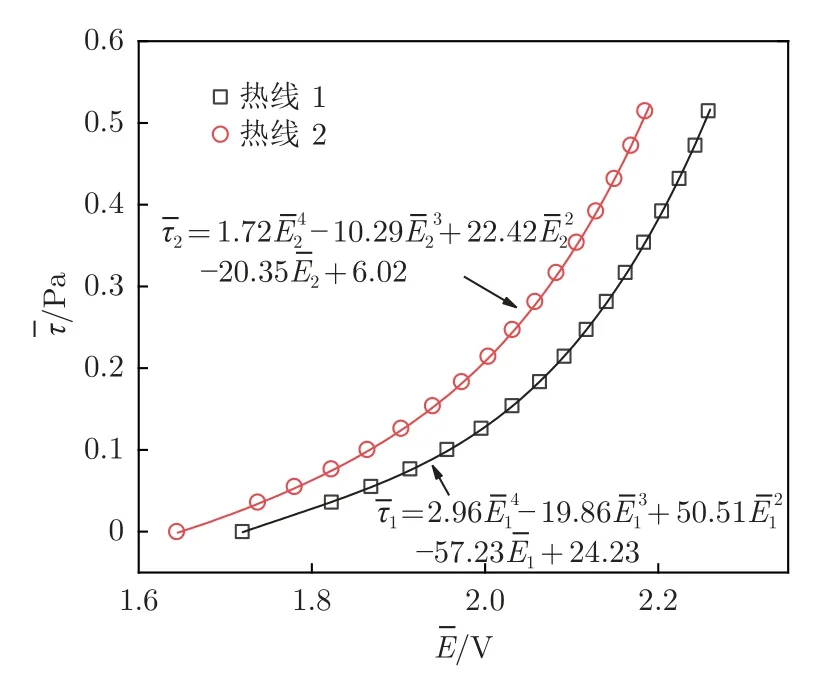
图6 平行双丝热线标定结果Fig.6 Calibration curves of parallel double hot wire

基于四次多项式拟合建立壁面摩擦应力与热线电压之间的关系，根据Coles-Fernholz 经验模型数据（如图7 所示），可估计出Reθ< 5 270 范围内的湍流边界层平均摩擦应力小于0.4 Pa，说明标定数据满足湍流边界层的测量需求。完成标定后，选取=0 标定点对应的2 根热线电压差均值作为摩擦应力方向判断阈值，其物理意义在于：当摩擦应力由正向变为负向或由负向变为正向时，必会经过τ=0，因此τ=0 可视为摩擦应力方向改变的临界点。

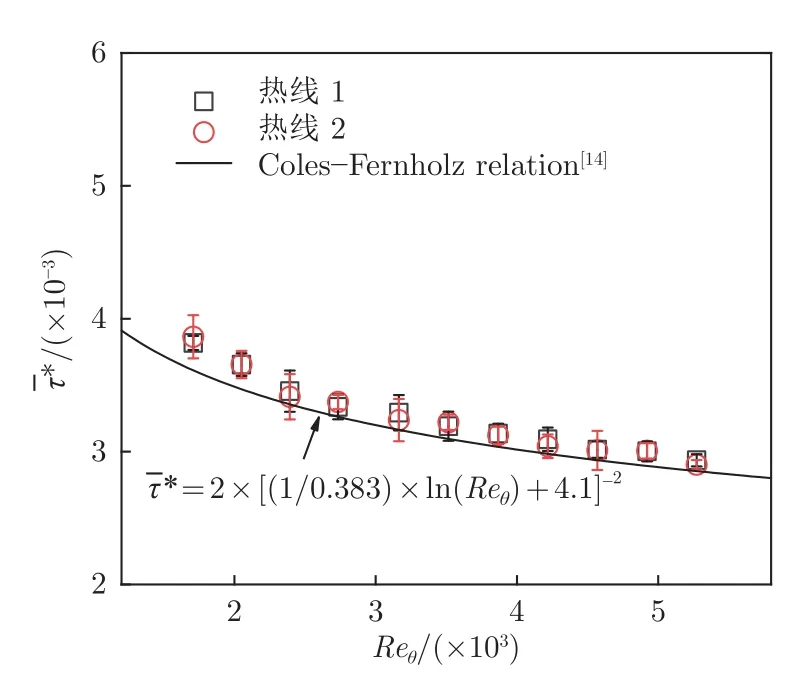
图7 不同雷诺数下平板湍流边界层平均摩擦应力测量结果Fig.7 Results of time-averaged shear stress in flat plate TBL at different Reynolds numbers

为验证平行双丝热线测量摩擦应力的可靠性，对距平板（有绊线）前缘1 m 处的零压梯度平板湍流边界层壁面摩擦应力进行测量。测量时，将热线1 和2 分别置于上游位置测得摩擦应力。测量结果如图7 所示（无量纲平均摩擦应力=/0.5ρU02）。与Coles-Fernholz 经验模型[14]相比，热线1 和2 测得的壁面摩擦应力的平均相对误差分别为3.6%和3.3%，平均相对不确定度分别为2.7%和3.0%（95%置信度），验证了摩擦应力测量的准确性。

湍流会增大流体热传导系数[15]，因此，利用考虑壁面效应影响的层流边界层标定的热线测量湍流边界层时，会略低估流体带走的热量，导致测量的速度略偏高，这是图7 中的实测数据比Coles-Fernholz 经验模型数据略高的原因。但平均偏差小于3.6%，仍然满足测试要求。

使用平行双丝热线对贴壁二维方柱下游壁面摩擦应力进行测量。如图8 所示，平行双丝热线探杆搭载于二维高精度滑台上，滑台可控制热线探针沿壁面法向（y 向）和流向（x 向）运动，快速扫描测量各流向位置的摩擦应力。热线1 置于上游，热线2 置于下游。对x/D=1～15 范围内（测量间距Δx/D=0.5）的壁面摩擦应力进行测量，热线采样频率为25 kHz，每个测点的采样时间为15 s，共重复测量4 次，获得摩擦应力统计特征。然后，结合平行双丝热线与TR-PIV，同步测量贴壁二维方柱下游流场和壁面摩擦应力。为避免PIV 激光直接照射热线，热线与PIV 测试面沿展向错开2.5 mm。流场测试区域为：1.5 < x/D < 8.5，0 < y/D < 4.3。壁面摩擦应力测点位置选取近壁面流向平均速度为0 处（x/D=7）。PIV 采样频率为1 kHz，平行双丝热线采样频率为25 kHz，同步采样时间为8 s。

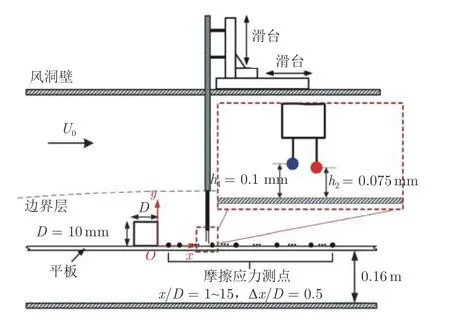
图8 贴壁二维方柱下游平板摩擦应力测量示意图Fig.8 Diagram of WSS measurement downstream of the wallmounted 2D square cylinder

2 结果与讨论

2.1 流动结构特征

在贴壁二维方柱的阻塞作用下，流动会在方柱上游壁面某处开始发生分离并“爬升”，之后在方柱前缘拐角附近发生二次流动分离[16]，在方柱下游形成回流区。图9（a）为贴壁二维方柱下游流场平均流向速度分布。以近壁面流向平均速度为0 处作为判据（图9 中白色等值线代表=0），可以得到流动再附点[6]位于壁面x/D=7 处，在x/D=7、y/D=4 处，=0.95U0，说明边界层厚度大于4D，即40 mm。图9（b）为贴壁二维方柱下游流场雷诺剪应力分布。可以发现，高雷诺剪应力区域主要分布于回流区与外部流动交界处的剪切层附近，在高雷诺剪应力区域下方，随着与壁面距离的减小，雷诺剪应力逐渐降低。理论上，壁面处流体的流向与法向脉动速度为0，因此壁面处流动雷诺剪应力为0。

图9 贴壁二维方柱下游流场统计特征量分布云图Fig.9 Contour of statistical values of flow field downstream of the wall-mounted 2D square cylinder

图10 给出了x/D=7 处雷诺剪应力沿法向的分布。受壁面光污染影响，距离壁面最近的PIV 测量位置为y/D=0.1，对应无方柱湍流边界层y+=45，与热线测量位置（y+=4.5）相比，距离壁面较远。但由图10 可以推断：随着y/D 减小，雷诺剪应力逐渐趋近于0，与流向速度梯度相比，雷诺剪应力为小量。因此，当法向位置无限趋近于壁面时，壁面附近流体受到的总剪应力壁面摩擦应力可直接由黏性底层速度梯度确定：值得注意的是，受PIV 采样频率限制，计算出的雷诺剪应力值相当于进行了低通滤波，图9（b）与图10 中的数值仅有参考价值，但仍能反映雷诺剪应力变化趋势。

图10 x/D=7 处流动雷诺剪应力沿法向分布Fig.10 Distribution of Reynolds shear stress of flow along normal direction at x/D=7

由于本文贴壁二维方柱完全浸没于湍流边界层中（δ/D=5），方柱前缘流动分离所产生的大尺度流动结构与众多小尺度非相干结构掺混在一起。为提取大尺度流动结构，采用降阶POD 重构方法[17-19]对方柱下游瞬时流场进行重构。本文使用前20 阶模态对流场进行POD 重构，保证重构后的流场所含有的脉动能量占原流场60%以上，并使用λci涡识别准则[20]对大尺度流动结构进行辨识。

本文重点关注流动分离区内（0 < x/D < 7）的流动结构特征。该区域流动结构丰富，且具有较强的涡旋与非定常特性。通过统计大量测试结果，将贴壁二维方柱下游流动结构进行分类。从方柱前缘产生的大尺度流动结构以2 种形式向下游运动，分别如图11 和12 所示（图中λci*=λciD/U0，λci基于瞬时速度场计算得到，其正负号与当地涡量一致；箭头表示瞬时脉动速度矢量）。在图11 中，黑框中从方柱前缘脱落的流动结构在向下游运动过程中发生分裂：红框中的子结构沿水平方向向下游运动，与壁面保持一定距离；绿框中的子结构向壁面运动，最终与壁面接触。在图12 中，黑框中从方柱前缘脱落的流动结构沿水平方向向下游运动，在运动过程中保持较为完整的形态。本文将流动结构分裂产生的向壁面运动的子结构（图11 绿框中的流动结构）称为“Ⅰ涡”，未分裂的流动结构（图12 黑框中的流动结构）及分裂产生的沿水平方向向下游运动的子结构（图11 红框中的流动结构）统称为“Ⅱ涡”。结合图11 和12 中的瞬时脉动速度矢量图可知：当Ⅰ涡与壁面接触时，接触点下游一段距离内出现强烈的下扫流动；当Ⅱ涡从壁面上方经过时，壁面附近出现局部回流。

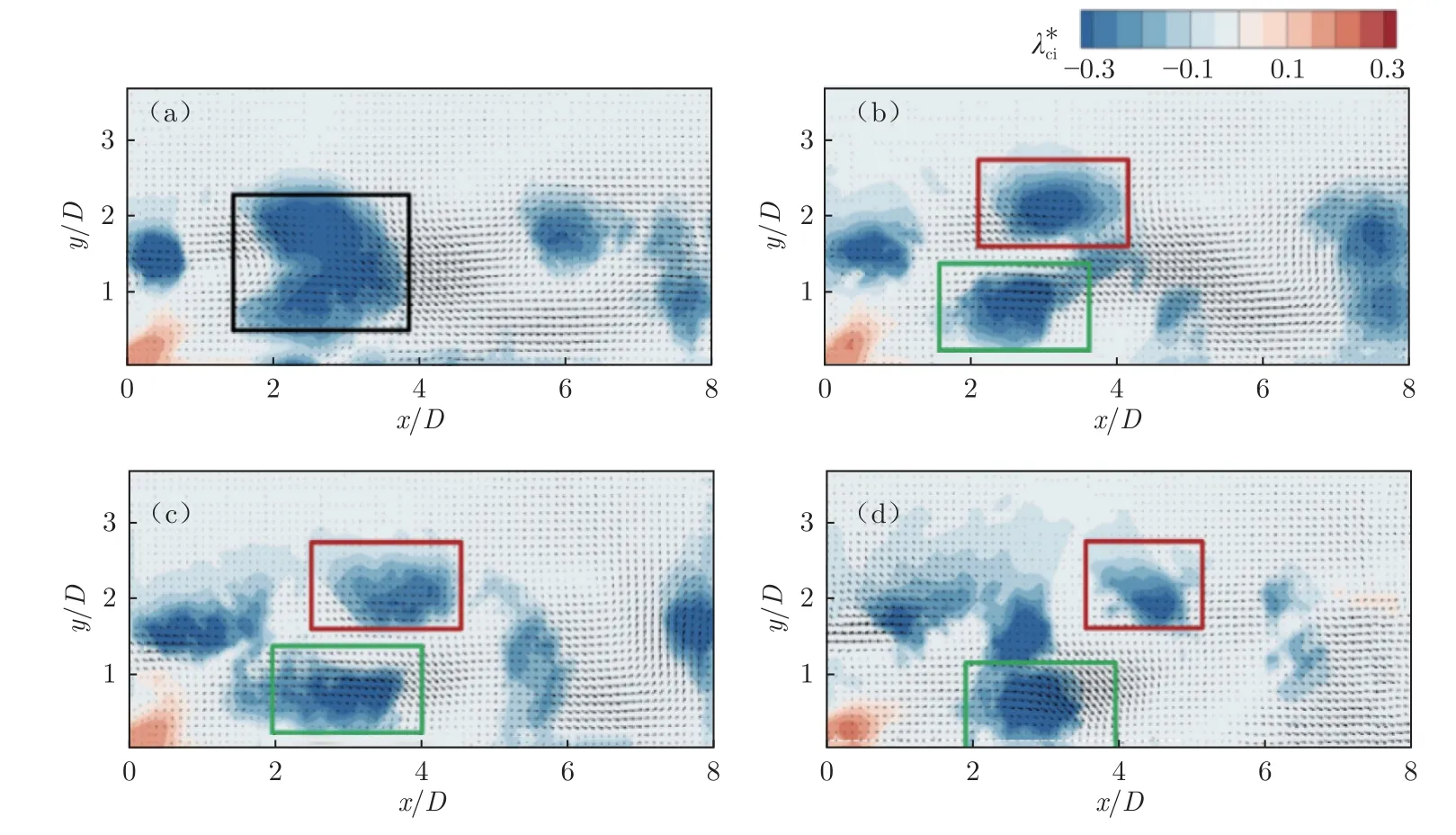
图11 贴壁二维方柱下游流动结构运动过程，4 图为连续时间序列，时间差1 msFig.11 Motion process of flow structure downstream of the wall mounted 2D square cylinder,where the four figures are continuous time series with interval of 1 ms

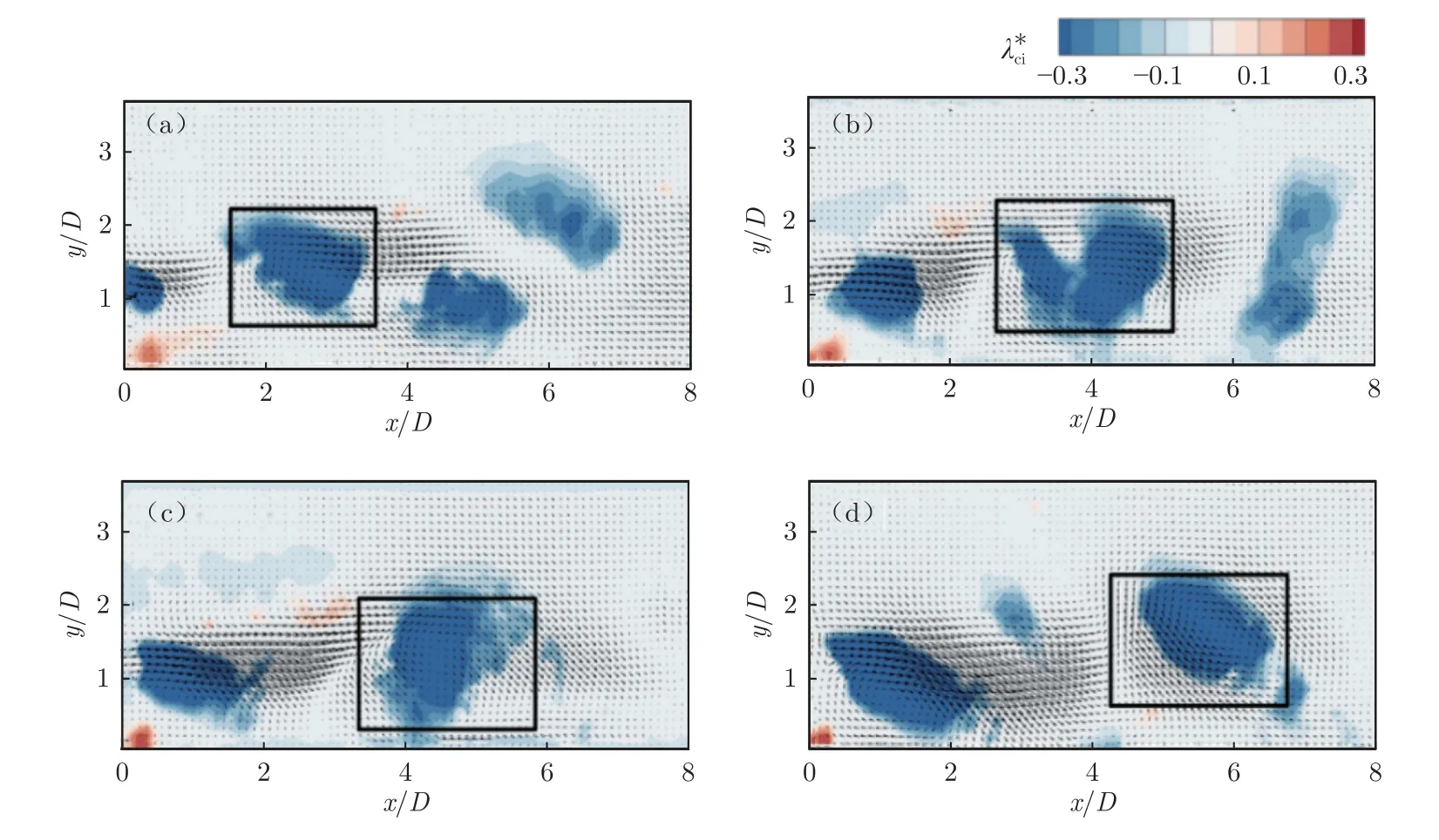
图12 贴壁二维方柱下游流动结构运动过程，4 图为连续时间序列，时间差2 msFig.12 Motion process of flow structure downstream of the wall mounted 2D square cylinder,where the four figures are continuous time series with interval of 2 ms

图13（a）和（b）分别为图11（a）和（b）流动结构分裂过程中的涡旋强度λci*等值线图。从图中可以发现，即将分裂的流动结构中存在2 个逐渐远离的高涡量区域，流动结构中心区域逐渐被低涡量流动占据，最终2 个涡量比较强的流体微团发生分离，该过程可能与流动的黏性耗散、湍流扩散及边界层外部流动的扰动作用有关。

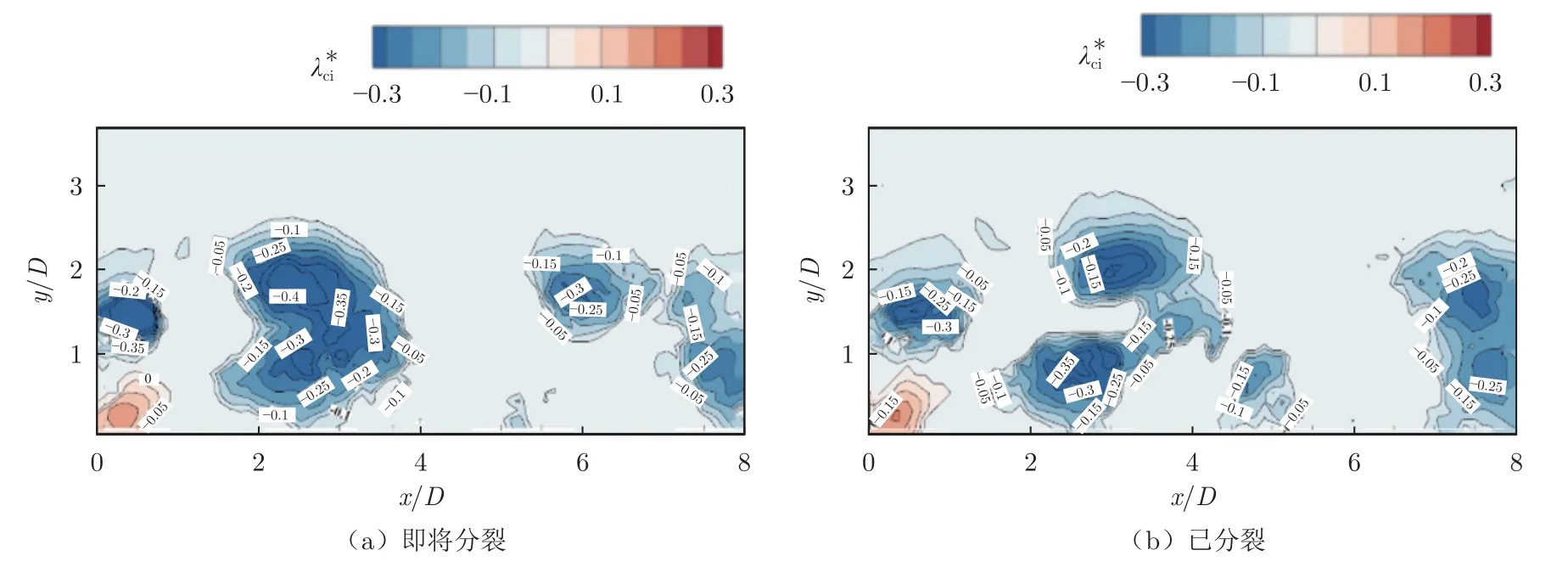
图13 流动结构分裂过程中的涡旋强度等值线图Fig.13 Vorticity intensity contour of flow structure during splitting

2.2 流动结构对测点壁面摩擦应力的影响

图14（a）为贴壁二维方柱下游壁面平均摩擦应力沿流向的分布，与壁面附近流场的平均流向速度分布（图9）高度一致。图14（a）中的平均摩擦应力0 值位置（x/D=7 附近）与图9 中的流动再附点位置（x/D=7）基本一致。图14（b）为摩擦应力回流间歇因子γτ（γτ为回流方向动态摩擦应力出现的时间占比）沿流向的分布。在流动再附点处（x/D=7），γτ接近0.5，说明该处来流方向、回流方向的摩擦应力时间占比相当。由上述结果可知，流动再附点处（x/D=7）的摩擦应力具有很强的非定常特性，动态摩擦应力在0 值附近频繁变化（即摩擦应力的方向在来流方向、回流方向之间频繁变化）。本文选取x/D=7 位置作为壁面摩擦应力测点，有利于分析特征流动结构对壁面摩擦应力的影响机理。

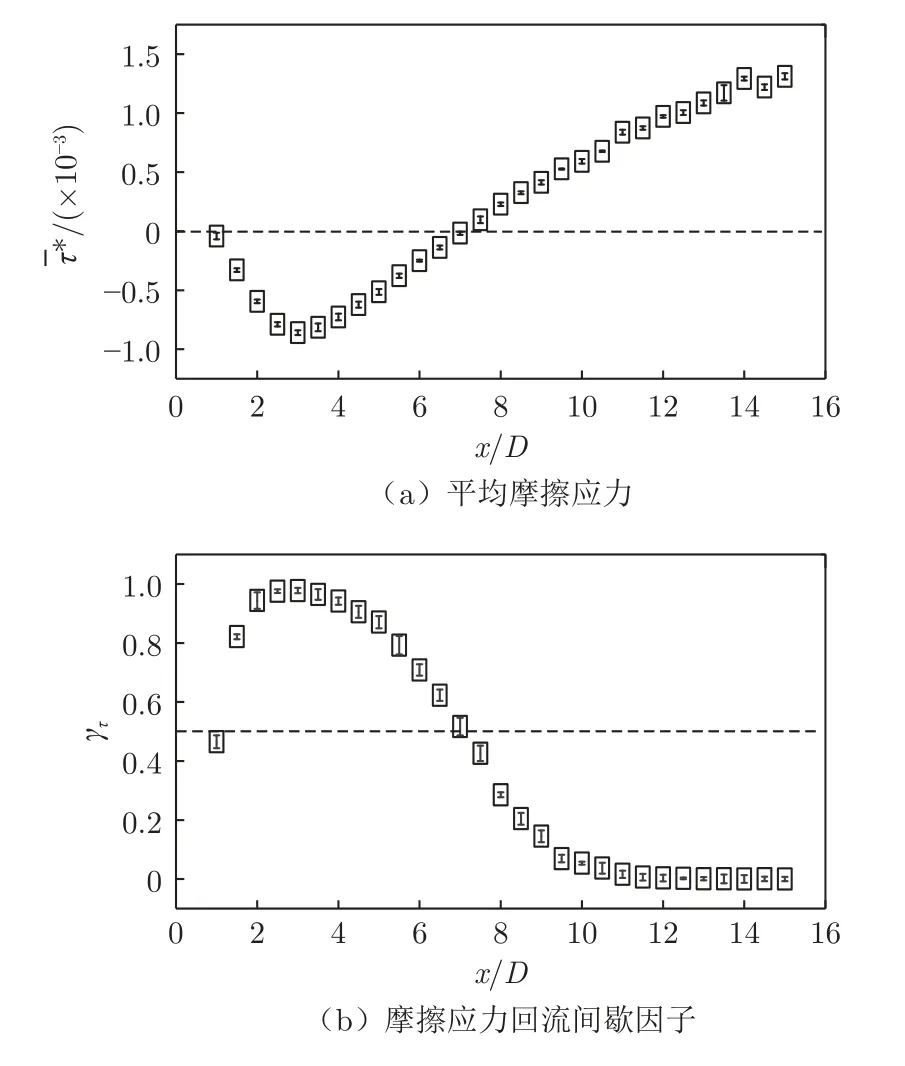
图14 贴壁二维方柱下游壁面摩擦应力统计值沿流向分布Fig.14 Distribution of statistical value of WSS along the flow direction downstream of the wall-mounted 2D square cylinder

图15 和16 分别为贴壁二维方柱下游流场、x/D=7 处壁面摩擦应力的同步测量结果。图15 为某些特征时刻对应的瞬时流场连续时间序列（时间间隔Δt=1 ms，箭头表示瞬时脉动速度矢量，使用λci准则进行涡识别）。图15 中的ta～tf时刻对应图16中标注的ta～tf时刻，tb、td、te对应Ⅰ涡出现的时刻，ta、tc、tf对应Ⅱ涡出现的时刻。在tb、td、te时刻附近时间段内，Ⅰ涡出现于摩擦应力测点上游并与壁面接触，在图14（b）、（d）、（e）红框中Ⅰ涡的诱导下，测点附近产生很强的下扫流动，使流向速度梯度向来流方向增大，测点壁面摩擦应力出现以下3 种变化：1）摩擦应力原为来流方向，Ⅰ涡的出现使摩擦应力绝对值陡增（tb时刻）；2）摩擦应力原为回流方向，Ⅰ涡的出现使摩擦应力绝对值锐减（td时刻）；3）摩擦应力原为回流方向，Ⅰ涡的出现使摩擦应力方向改变为来流方向（te时刻）。在ta、tc、tf时刻附近时间段内，图15（a）、（c）、（f）红框中的Ⅱ涡从测点上方经过，在壁面附近诱导出局部回流，使流向速度梯度向回流方向增大，测点壁面摩擦应力出现以下3 种变化：1）摩擦应力原为回流方向，Ⅱ涡的出现使摩擦应力绝对值陡增（ta时刻）；2）摩擦应力原为来流方向，Ⅱ涡的出现使摩擦应力绝对值锐减（tf时刻）；3）摩擦应力原为来流方向，Ⅱ涡的出现使摩擦应力方向改变为回流方向（tc时刻）。值得注意的是，虽然热线与PIV 测试面已沿展向错开2.5 mm，但热线探杆仍会对PIV 图像造成光污染，影响PIV 图像质量，使x/D=7 附近区域出现了流动结构破碎的假象，如图15（c）所示。

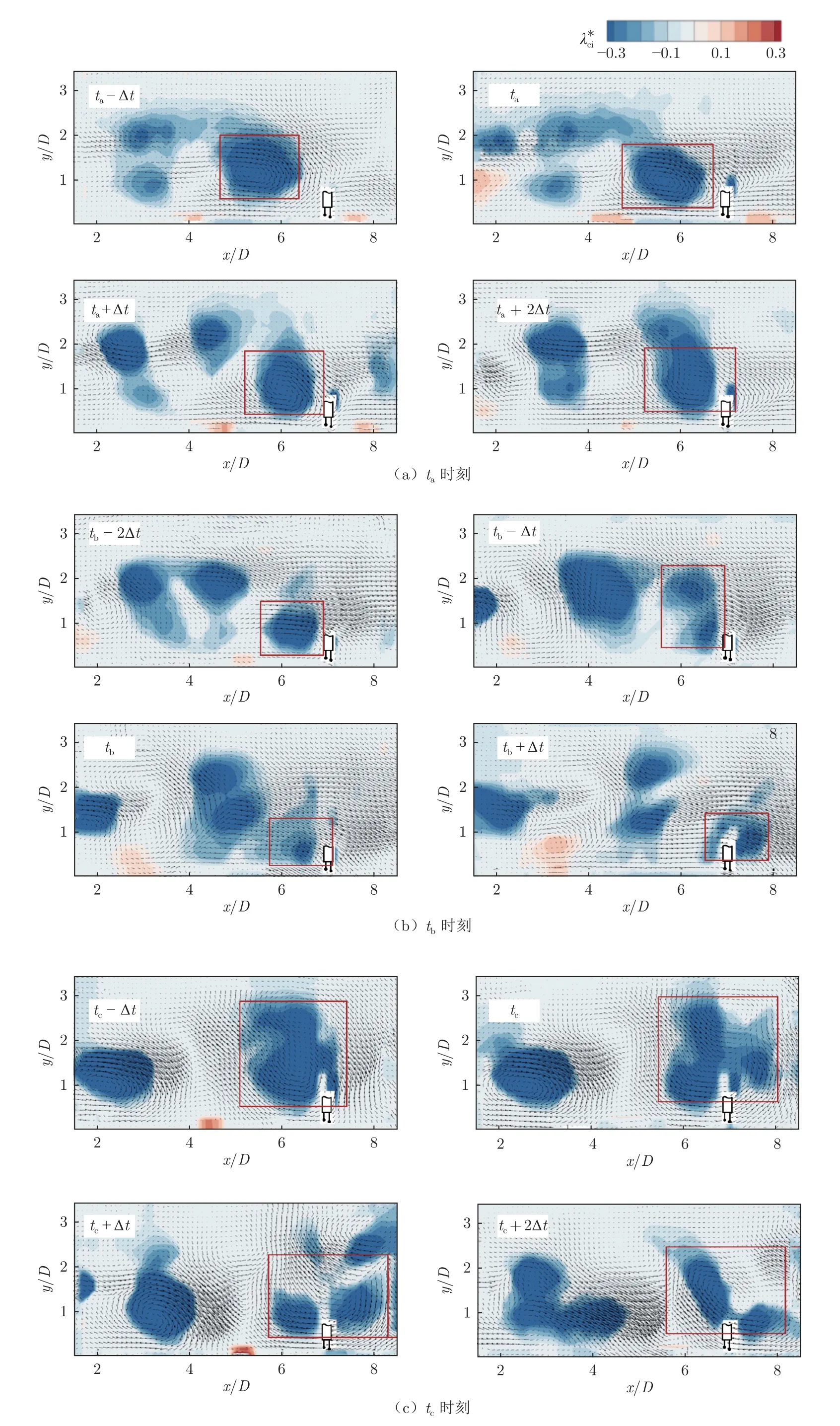
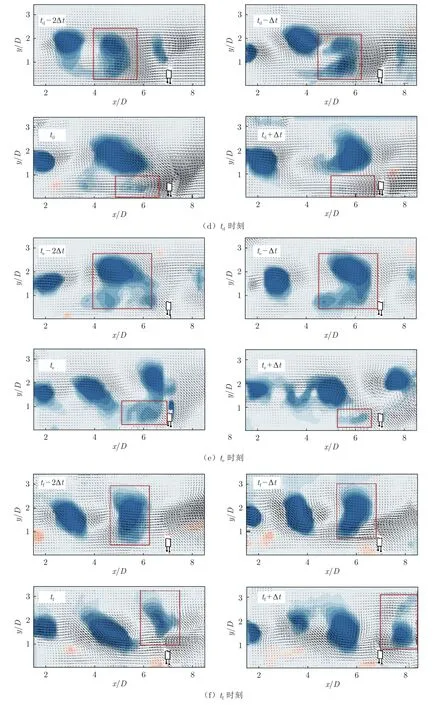
图15 贴壁二维方柱下游某些时间段内的瞬时流场Fig.15 Instantaneous flow field downstream of wall-mounted 2D square cylinder during certain time periods

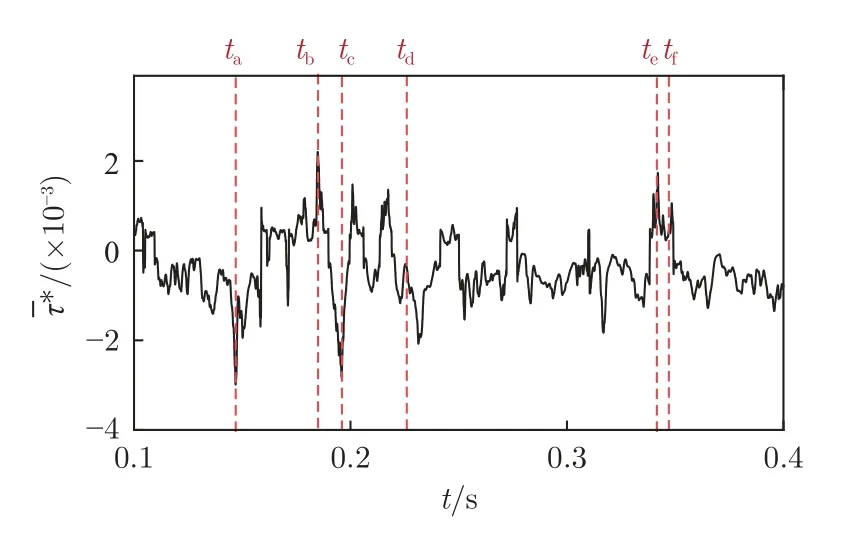
图16 壁面摩擦应力随时间变化曲线（x/D=7）Fig.16 Curve between WSS and time (x/D=7)

在壁湍流中，近壁面流向涡[21]也会对壁面摩擦应力造成影响。与上述Ⅰ涡、Ⅱ涡对壁面摩擦应力的影响机制类似，在流向涡的诱导下，涡结构的两侧分别出现上抛流动和下扫流动：上抛流动会使壁面附近出现低速条带，减小流向速度梯度，使摩擦应力值减小；下扫流动会增大壁面附近的流向速度梯度，使摩擦应力值增大[21]。不同之处在于，Ⅰ涡、Ⅱ涡为展向涡，不仅会改变摩擦应力大小，还会改变摩擦应力方向。

3 结 论

本文利用平行双丝热线和TR-PIV 研究了贴壁二维方柱下游流动结构对壁面摩擦应力的影响机制。流动经过贴壁二维方柱，会产生2 种典型的大尺度流动结构：向壁面靠近并接触壁面的近壁流动结构（Ⅰ涡）；平行壁面沿流向运动的流动结构（Ⅱ涡）。Ⅰ涡、Ⅱ涡的出现改变了壁面附近流动速度的大小和方向、影响了测点壁面摩擦应力：增大了流向速度梯度，导致摩擦应力陡增；减小了流向速度梯度，导致摩擦应力锐减；改变了摩擦应力方向。