合成射流激励器能量转换效率的参数影响规律及优化研究

王雷，李哲，冯立好

北京航空航天大学 流体力学教育部重点实验室，北京 100191

0 引 言

到2050 年，实现“净零碳排放”是世界各国航空业发展的重要战略目标。对于大型飞机，减小阻力、提高燃油效率是降低碳排放的必然选择。以美国C-17 运输机为例，阻力每降低1%，每年可节省710 万加仑（约 26876 m3）燃油[1]。流动控制是实现上述目标的重要途径之一。流动控制技术可分为被动流动控制技术和主动流动控制技术。主动流动控制技术通过向流场局部注入少量能量，即可改变局部甚至全局流场的自然发展路径，具有较高的控制效率[2]。各种形式的激励器是主动流动控制技术的核心，其性能制约着流动控制技术的发展和应用[3]。开展激励器参数影响规律研究、优化激励器性能，对于提高流动控制效率、拓展流动控制的应用领域具有重要意义。

合成射流激励器是当前应用最为广泛的激励器之一[4-6]，主要通过周期性吹吸气诱导产生离散的旋涡结构，对外部流场施加控制，具有对外输出质量流量为零、输出动量不为零的特点，因此也被称为“零质量射流激励器”。根据射流产生方式的不同，合成射流激励器可分为活塞驱动式[7]、压电薄膜振动式[8]、声激励式[9]和电磁振动式[10]等。其中，压电式合成射流激励器主要由压电膜片和带有射流出口的腔体组成，具有结构简单、体积小、成本低等优点。此外，相比其他形式的激励器，压电式合成射流激励器的射流速度高、频率高（最大射流速度可达数十米至上百米每秒，激励频率可达数百至上千赫兹[3]）。基于上述性能优势，压电式合成射流激励器在抑制流动分离[11]、提高传热[12]、增强掺混[13]、降低噪声[14]、控制推力矢量[15]等方面控制效果突出，具有良好的工程应用前景。

射流出口速度峰值和能量转换效率是衡量压电式合成射流激励器性能的重要指标。为了提高压电式合成射流激励器的性能，研究人员对其参数影响规律开展了大量研究。Tang 等[8]对圆形出口合成射流进行研究，发现随着出口直径的减小，射流出口速度峰值先增大，随后在管道黏性的影响下，速度峰值逐渐减小。Wang 等[16-18]开展了非圆出口合成射流的系列研究，发现出口形状对流场特征影响显著，非圆出口合成射流能够极大提高射流出口附近的脉动速度峰值。Gomes 和Crowther[19]发现，当腔体和压电膜片的固有频率相近时，压电式合成射流激励器能够获得最大的出口速度和能量转换效率；此外，出口速度随出口深度和腔体高度的增大而减小。Van Buren 等[20]发现，压电式合成射流激励器的出口速度随着压电膜片直径的增大而增大。Gungordu[21]发现，在相同激励电压和压电膜片固有频率下，双面驱动压电膜片产生的中心位移和出口速度均为单面驱动压电膜片的1.5 倍。经过参数优化后，双面驱动压电膜片产生的最大出口速度峰值达到92.1 m/s，但对应能量转换效率仅为6.4%；此外，当出口速度峰值为57.6 m/s 时，能量转换效率最大，达到30.3%。

以上研究表明，通过优化合成射流激励器参数能够提高激励器性能。合成射流激励器本质上是一种能量转换装置，在追求高动量输出的同时应尽量降低激励器能耗。但现有研究对影响激励器能量转换效率的参数关注不足，导致在获得较高射流出口速度的同时，能量转换效率普遍较低。

针对上述问题，本文开展压电式合成射流激励器参数影响规律及性能优化研究，探索出口长度、出口深度、腔体高度和陶瓷片厚度等参数对其性能的影响规律，并通过参数优化设计，提高其最大出口速度和能量转换效率，为研制高动量低能耗激励器、提升合成射流的控制效率提供技术支撑。

1 实验装置及方法

1.1 压电式合成射流激励器参数

本文采用的压电式合成射流激励器（后文简称激励器）模型如图1 所示。激励器主要由激励器底板、压电膜片、O 型圈、激励器盖板等部分组成（压电膜片与激励器底板之间的空间构成腔体，射流出口位于激励器底板一侧）。激励器底板和盖板以光敏树脂材料经3D 打印加工而成，装配后尺寸为75 mm × 65 mm × 11 mm，腔体直径Dc=48 mm。压电膜片由高弹性磷铜片和PZT-5X 压电陶瓷片贴合而成（铜片直径ϕCu=50 mm，厚度δCu=0.35 mm；陶瓷片直径ϕp=40 mm），采用双面驱动形式。射流出口为矩形，出口宽度ho=1 mm。

图1 压电式合成射流激励器组成部件及腔体截面示意图Fig.1 Schematics of components and cavity section of piezoelectricdriven synthetic jet actuator

实验研究了出口长度lo、出口深度no、腔体高度hc和陶瓷片厚度δp对激励器性能的影响规律。铜片厚度对激励器出口速度峰值影响较小，本文未予关注。根据已有研究[20]，以出口宽度ho为特征长度对各参数进行无量纲化（lo∗=lo/ho，n∗o=no/ho，h∗c=hc/ho，δ∗p=δp/ho），表1 列出了各参数的取值情况。当研究某一参数的影响规律时，其余参数与基准工况保持一致，并将实验结果与基准工况进行对比。

表1 合成射流激励器参数Table 1 Synthetic jet actuator configuration parameters

1.2 激励器出口速度及功率测量

实验测量系统主要包括激励器能量输入模块和激励器性能测量模块两部分，由AFG1062 信号发生器、ATA-214 电压放大器（电压增益：0～100 倍可调，最大输出电压峰-峰值Up-p：400 V，电流：300 mA）、SDS1102X+数字示波器、TH3431 电子功率计、压电式合成射流激励器、热线探针、航华CTA-02A 热线风速仪、NI USB-6259 数据采集卡和数据后处理系统等组成，如图2 所示，其中P(t)为瞬时功率，u(t)为瞬时出口速度。实验过程中，首先由信号发生器产生具有一定幅值和频率的正弦波信号，经电压放大器放大后，输入到压电式合成射流激励器。信号发生器和电压放大器分别调节激励器的频率f和电压峰-峰值Up-p。压电膜片在一定电信号激励下产生特定的振动或变形，挤压腔体内空气，在出口形成合成射流。

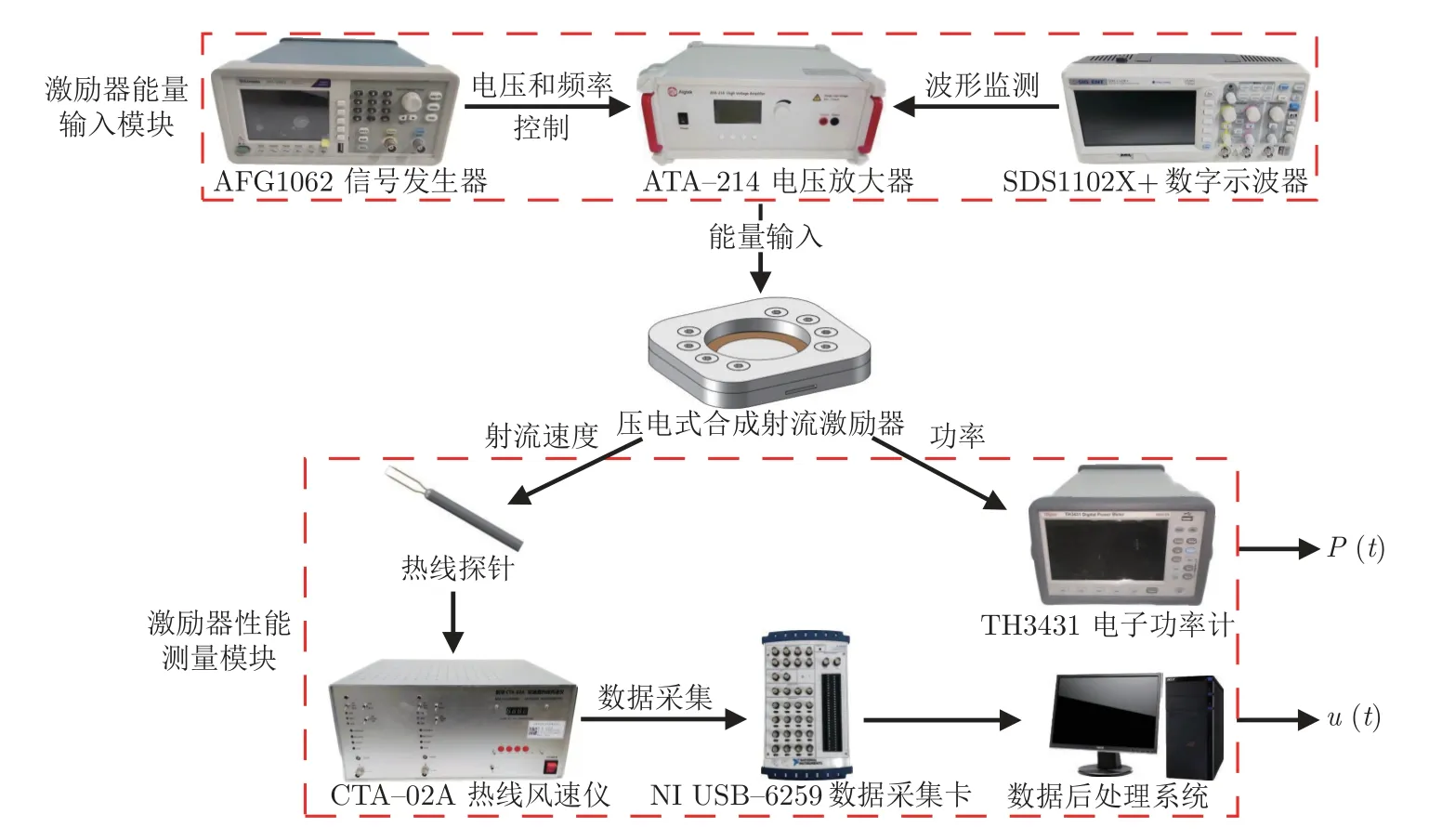
图2 实验测量系统Fig.2 Experimental measurement system

在激励器工作期间，利用数字示波器对输入信号进行实时监测，以保证输入波形不失真且幅值不过载。利用热线风速仪测量激励器瞬时出口速度u(t)，热线探针通过三轴位移台调整至矩形出口长轴所在平面，采样频率为20 kHz，采样时间为10 s。测量数据由数据采集卡采集储存，并通过数据后处理系统进行处理。此外，利用电子功率计同步记录激励器的瞬时功率P(t)，采样频率为5 Hz，采样时间为10 s。取功率稳定后的数据进行时间平均，得到对应激励条件下的激励器平均功率。

图3 展示了某一激励条件下，利用热线获得的基准工况射流出口处不同流向位置瞬时速度随时间t 的变化，x∗为用出口宽度无量纲化的流向坐标（x∗=x/ho）。结果显示，射流出口速度表现出较好的周期性，每周期（1.6 ms）内存在2 个峰值，分别为吹程和吸程阶段的速度峰值，注意实际吸程速度为对应数值的负值。激励器出口具有一定深度，在吸程阶段，出口深度会导致对出口周围流体吸入强度显著减弱，且距离出口越远，吸入强度越弱，因此，测得的吸程速度峰值小于吹程速度峰值。通过提取每个周期内出口速度的最大值并进行时间平均，得到图3 激励条件下的出口速度峰值=74 m/s。

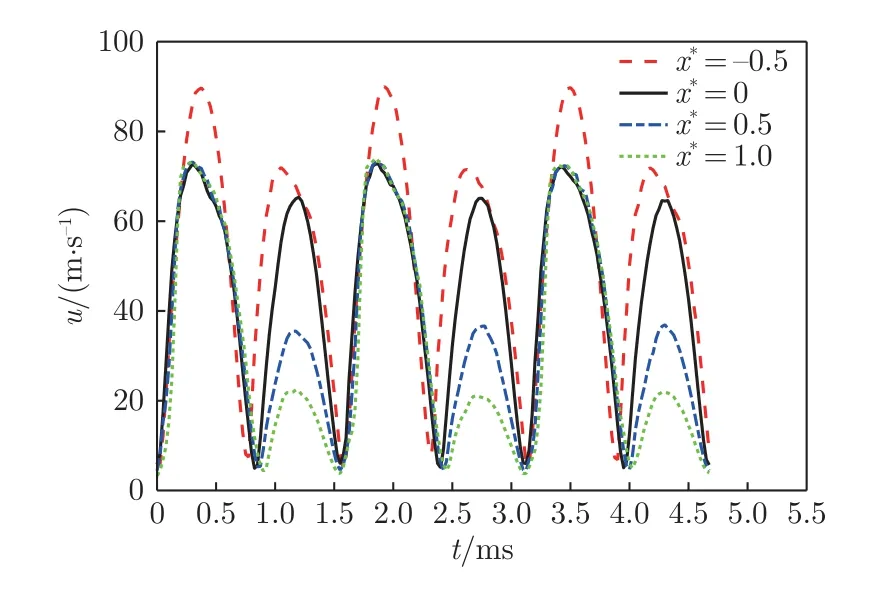
图3 基准工况射流出口不同流向位置瞬时速度随时间的变化Fig.3 Variation of instantaneous velocity at different streamwise locations from the exit of the baseline actuator

1.3 激励器能量转换效率计算

本文采用与已有研究[14,20-23]相同的方法计算激励器的能量转换效率：

Wjet为射流总动能，可表示为：

式中：τ为射流喷出的持续时间，在本实验中为10 s；为激励器出口的质量流率，=ρalohou(t)，ρa为空气密度。

Win为激励器消耗的电能，可对瞬时功率进行积分得到：

2 实验结果及分析

2.1 基准工况特性

对基准工况的激励器特性进行了详细研究，结果如图4 所示：激励器出口速度峰值呈现出双峰频率特征（图4（a）），分别对应了压电膜片的固有频率fD（620 Hz）和亥姆霍兹频率fH（1060 Hz）。

图4 基准工况的激励器特性Fig.4 Characteristics of the baseline actuator

亥姆霍兹频率主要由激励器几何构型参数决定，表示为[22,24]：

式中：c 为声速。将基准工况的参数代入式（4），得到fH=1 039Hz，这与实验测得的第2 个峰值1060 Hz接近。

压电膜片的固有频率与压电膜片的物理性质和固定方式相关，可通过以下公式[24]进行估计：

式中：δD、R、E、ρD、ε分别为压电膜片的厚度、半径、弹性模量、密度、泊松比；ξ为经验衰减因子（ξ=0.06）；k2为无量纲频率参数，与压电膜片的固定状态相关（简支状态k2=4，固支状态k2=10）。本实验压电膜片由磷铜片和压电陶瓷贴合而成，对于磷铜片（E=89 Gpa，ρD=8 900 kg/m3，ε=0.35），根据式（5）计算得到fD=815 Hz；对于压电陶瓷（E=63Gpa，ρD=7 600 kg/m3，ε=0.3），根据式（5）计算得到fD=488 Hz。实验测得的第1 个峰值620 Hz 位于这2 个频率之间，因此对应了压电膜片的固有频率。由于激励器在固有频率下产生了最大的出口速度峰值，因此选择该频率作为衡量激励器性能的最佳激励频率，后文分析采用同样的思路。

结合图4（b）～（d）可以发现：在最佳激励频率下，随着电压增大，激励器出口速度峰值近似呈线性增长，消耗的平均功率逐渐增大，但对应的能量转换效率逐渐降低。这表明当激励器出口速度较大时，输入激励器的电能只有少部分转化为射流的动能，大部分能量由于激励器温度和压电膜片振动噪声升高，转化为热能和声能。针对该问题，本文通过优化激励器参数组合，在提高激励器出口速度的同时，改善激励器的能量转换效率，降低其能量损失。

2.2 激励器参数影响规律

2.2.1 出口长度

图5 展示了不同出口长度的激励器出口速度峰值和能量转换效率随平均功率的变化。当输入平均功率相同时，随着出口长度增大，出口截面积增大，出口速度减小；能量转换效率随出口长度增大而增大，且增大幅值明显大于出口速度的减小幅值。例如，在平均功率约3.2 W 时，lo∗=25工况下的能量转换效率相比lo∗=10提高了107.4%，但出口速度峰值仅减小了4.7%。这是由于，在出口速度减小的同时，较大的出口截面积增大了质量流量，且后者增大的速率高于前者减小的速率。在较大的平均功率下，lo∗=20和lo∗=25工况的出口速度峰值接近，但lo∗=25工况明显具有更大的能量转换效率，因此，选取l∗o=25作为优化激励器的出口长度。

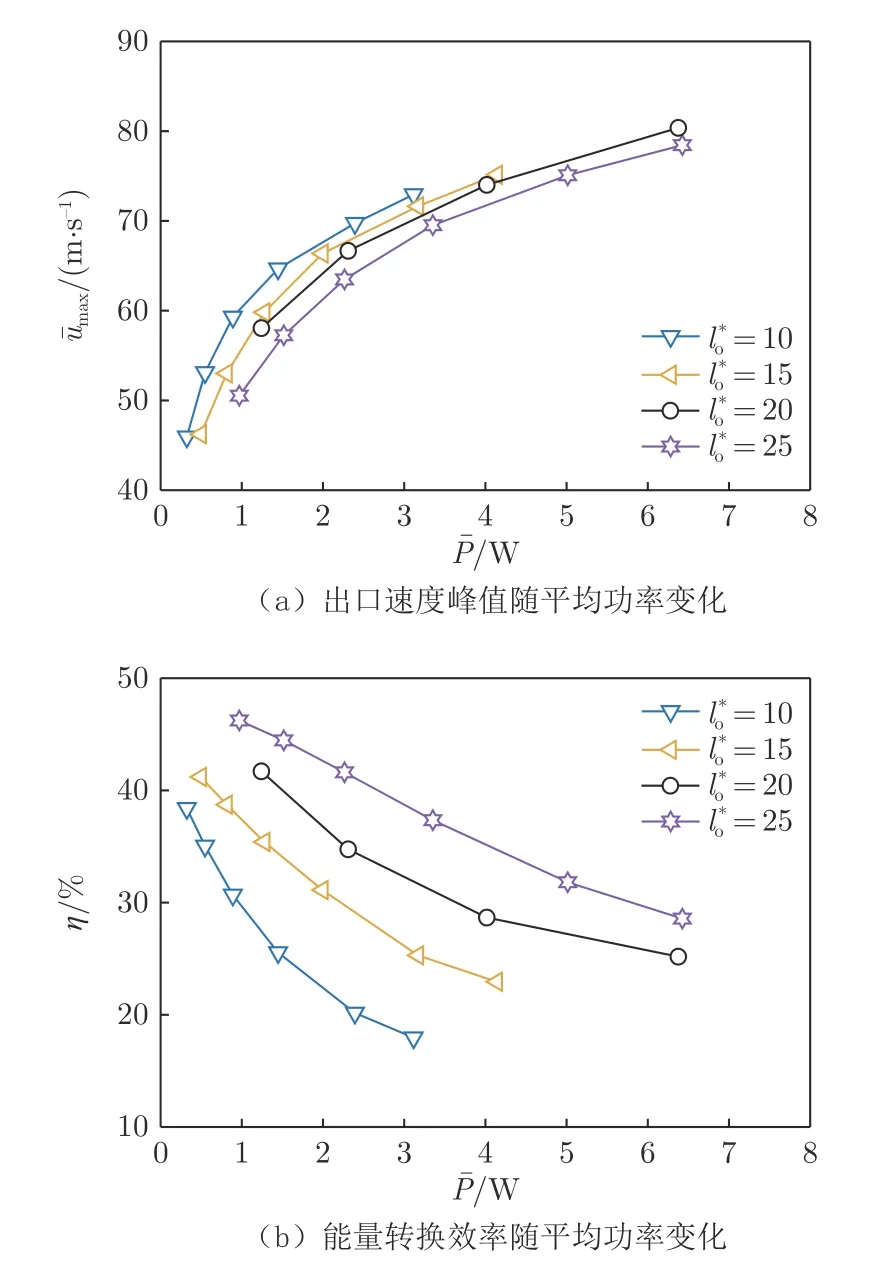
图5 不同出口长度的激励器特性Fig.5 Characteristics of the actuators with different orifice lengths

2.2.2 出口深度

出口深度对激励器性能的影响规律如图6 所示。总体上，相同平均功率下出口深度对出口速度峰值的影响并不显著。但是，n∗o=12.5工况的出口速度峰值和能量转换效率均大于其他工况。已有研究[19,23]表明：当出口深度较小时，空气在射流出口内部产生流动分离，不足以维持附着流动，使得出口速度减小；随着出口深度增大，在出口收缩效应作用下，射流速度提高；当出口深度较大时，在管道黏性影响下，出口速度减小。因此，存在一个最优出口深度，使得出口速度峰值及能量转换效率达到最优。在本文研究中，选取n∗o=12.5作为优化激励器的出口深度。

图6 不同出口深度的激励器特性Fig.6 Characteristics of the actuators with different orifice neck lengths

2.2.3 腔体高度

腔体高度对激励器性能的影响规律如图7 所示。当输入平均功率相同时，随着腔体高度增大，出口速度峰值和能量转换效率均增大。值得注意的是，压电式合成射流激励器出口速度峰值随腔体高度的变化规律与腔体高度的大小相关。Lockerby 和Carpenter[25]建立了圆形出口压电式合成射流激励器的可压缩计算模型，研究了出口速度峰值随腔体高度的变化规律，发现当腔体高度在一定范围内时，出口速度峰值随腔体高度增大而增大，随后出口速度峰值随腔体高度增大而减小，即存在一个最优腔体高度使得出口速度峰值达到最大。

图7 不同腔体高度的激励器特性Fig.7 Characteristics of the actuators with different cavity heights

Gomes 和Crowther[19]、Van Buren[20]、Rizzetta[26]和Mane[27]等分别研究了腔体高度对激励器出口速度峰值的影响。汇总相关结果发现，当腔体高度明显小于出口直径（对于矩形出口，出口直径为等效圆直径De）时，出口速度峰值随腔体高度增大而增大；当腔体高度大于出口直径时，出口速度峰值随腔体高度增大而减小，这与Lockerby 和Carpenter[25]发现的规律一致。本文的压电式合成射流激励器腔体高度明显小于出口直径（hc/De=0.30～0.50），因此，出口速度峰值和能量转换效率随腔体高度增大而增大。本文选取h∗c=2.5作为优化激励器的腔体高度。

2.2.4 陶瓷片厚度

陶瓷片厚度对激励器性能的影响规律如图8所示。在相同平均功率下，随着陶瓷片厚度减小，出口速度峰值和能量转换效率均增大，同时激励器所能承受的最大平均功率增大。这是因为随着厚度减小，陶瓷片的弯曲性能增强，使得压电膜片的振幅增大，从而提高了腔体内空气压缩的体积变化率，导致出口速度和能量转换效率提高。此外，Van Buren[20]、Chen[28]和邓雄[29]等的研究均表明，随着陶瓷片厚度增大，刚度增大，导致激励器出口速度峰值减小。因此，选取δ∗p=0.15作为优化激励器的陶瓷片厚度。

图8 不同陶瓷片厚度的激励器特性Fig.8 Characteristics of the actuators with different piezoceramics thicknesses

图9 统计了上述不同参数的激励器出口速度峰值随平均功率的变化，并对数据进行了多项式拟合，如红色实线所示。结果显示，所有工况的出口速度峰值随平均功率变化的趋势相似，即随着平均功率的增大，出口速度峰值先迅速增大随后逐渐趋于稳定。这表明激励器出口速度峰值与平均功率的关系对激励器参数并不敏感。

图9 不同参数的激励器出口速度峰值随平均功率变化Fig.9 Exit peak velocity versus power for actuators with different configuration parameters

2.3 激励器性能优化

基于上述参数影响规律对激励器进行了优化设计，优化后的参数组合方案如表2 所示。优化后的激励器特性如图10 所示，并与基准工况进行了对比。在所有测量电压下，优化工况的出口速度峰值均大于基准工况（提升了9.0%～15.3%）。此外，当=2 W时，基准工况和优化工况的出口速度峰值均约为67 m/s，但是优化工况的能量转换效率比基准工况提升了23.5%；当基准工况和优化工况消耗的平均功率达到最大时，能量转换效率均在22%左右，但是优化工况的出口速度峰值达到了93.0 m/s，比基准工况提升了9.3%。以上结果表明：经参数优化后，激励器性能获得了明显改善，出口速度峰值和能量转换效率均得到了提升。

表2 合成射流激励器优化后的参数Table 2 Optimized synthetic jet actuator configuration parameters

图10 优化工况的激励器特性Fig.10 Characteristics of the optimized actuator

图11 为本文优化激励器的性能与已有研究结果[14,20-22]的对比。可以看到，激励器的出口速度与能量转换效率负相关。本文优化后的激励器相比已有同类型的激励器具有更高的能量利用率。例如，与Gungordu[21]出口速度峰值最大工况相比，能量转换效率提升了233.3%；与其能量转换效率最大工况相比，出口速度峰值提升了42.2%。与Crowther 和Comes[22]能量转换效率最大工况相比，在略增大出口速度峰值的同时，能量转换效率提升了163.8%。需要指出的是，Van Buren 等[20]与Crowther 和Comes[22]的激励器最大出口速度峰值超过了120 m/s，本文在测量的电压范围内并未达到该水平。为了进一步提高激励器的出口速度，需要开展更深入的研究。但是，在较高出口速度下，激励器的能量转换效率显著偏低，这对提高激励器的能量利用率提出了更大的挑战。

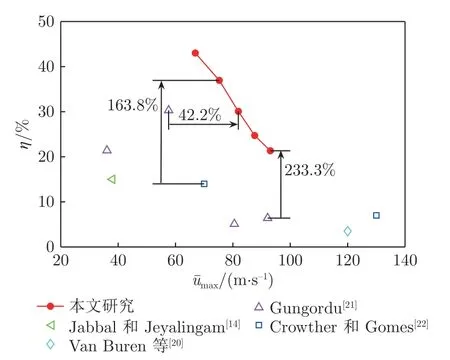
图11 本文优化的激励器性能与已有研究结果[14,20-22]对比Fig.11 Comparison of performance between the present optimized actuator and previous ones[14,20-22]

3 结 论

为提高压电式合成射流激励器性能，本文开展了激励器出口长度、出口深度、腔体高度和陶瓷片厚度对出口速度峰值和能量转换效率的影响规律研究，得到结论如下：

对于本文的激励器构型，当输入平均功率相同时：1）随着出口长度增大，出口速度峰值减小，能量转换效率增大；2）存在一个出口深度的最优值，使得出口速度峰值和能量转换效率达到最大；3）本文的腔体高度（腔体高度显著小于射流出口等效直径）范围内，随着腔体高度增大，出口速度峰值和能量转换效率均增大；4）随着陶瓷片厚度增大，出口速度峰值和能量转换效率均减小。

特别地，本文发现对于上述不同参数，激励器出口速度峰值随平均功率的变化趋势相似，并得到了相应的拟合曲线。通过优化参数组合，提高了激励器出口速度峰值，优化工况的出口速度峰值达到93.0 m/s，比基准工况提升了9.3%。此外，与已有研究结果相比，本文优化的激励器有效提升了能量转换效率（最大提升了233.3%），具有显著的性能优势。