柔性互联配电网故障恢复的云边协同优化算法

徐展鹏，梁远升，李海锋，王 钢，李 佳

（华南理工大学电力学院，广东省 广州市 510641）

0 引言

近年来，随着分布式电源（distributed generator，DG）渗透率日渐提高和柔性电力电子技术高速发展，柔性互联的主动配电网（active distribution network，ADN）被提出［1-2］。对比传统配电网，ADN可协调控制各种可控DG、储能系统（energy storage system，ESS） 、柔 性 互 联 设 备（flexible interconnected device，FID）及无功设备等，实现网络间弹性能源互济［3-5］。当ADN 出现停电故障时，FID可灵活控制各端口功率或切换为孤岛控制模式，结合配电网故障恢复策略协调优化各ADN 的功率调度，保障配电网持续可靠的优质电力供应［6-7］。

配电网的故障恢复通常包括两个范畴：一种是指短路故障等导致配电网失压停电，在故障辨识、定位与隔离后，执行网络重构与孤岛划分的紧急调度策略［8-11］；另一种是指因气候等灾害因素导致的配电网大范围停电的故障修复时序优化策略［12-13］。本文针对柔性互联配电网，重点关注配电网短路故障后，如何利用FID 协同多个互联网络实现快速转供电和紧急优化调度策略。

针对单一ADN 的故障恢复，现有研究借助ADN 的DG、ESS 等通过网络重构或孤岛划分等方式，考虑尽可能多的负荷恢复量，减少损耗成本，将故障恢复抽象为多目标的组合优化问题［14］。常用的优化求解算法包括以支路和节点优先级作为规则，采取“搜索+调整”思路进行求解的启发式搜索算法［15］，以及采用多次迭代、概率寻优方式的智能优化算法［16-17］，或采用二阶锥松弛的配电网潮流约束的混合整数二阶锥规划（mixed-integer secondorder cone programming，MISOCP）优化算法［18-19］。

针对柔性互联的多ADN 网络，FID 的接入充分发挥了其在故障恢复中的电压支撑和功率灵活调控的作用［20-23］。文献［24］建立了多端口FID 的互联ADN 故障恢复优化模型，采用MISOCP 方法统一求取ADN 各设备运行指令的调节方案。文献［25］考虑了DG、ESS 和FID 之间的协调控制，采用鲁棒优化的方法求取ADN 故障恢复的孤岛划分调节方案。这些方法的提出，为配电网故障恢复方案提供了最优决策方案，有利于更大范围的供电恢复。

由于柔性互联的多个ADN 增加了故障恢复优化问题的维度和规模，故障恢复策略的计算与执行的耗时变长。针对大规模网络的优化求解问题，在电力系统的优化调度领域，分布式优化计算方法常被用于解决信息与算力的分配问题，如目标级联分析法［26-27］、交替方向乘子法（alternating direction method of multipliers，ADMM）［28-29］等。这些方法将优化调度问题分由多个分布式智能体联合迭代求解，通过多智能体之间的合作协调完成优化的任务，在多ADN 间的优化调度上发挥了积极的作用。但是，由于这些方法往往要依靠多轮信息交互与迭代才能得到计算结果，信息多次交互的通信延时和迭代不利于故障恢复紧急决策的快速响应。

近年来，新兴的边缘计算云边协同技术将原本集中的计算、存储和应用等功能部分转移至网络边缘，提供了一种信息预处理的云边网络架构，能有效聚合网络边缘的计算资源，支撑故障恢复等紧急业务的快速响应［30］。利用分布于边缘网络的算力在闲时预先处理边缘内部的网络数据，将边缘网络功率交互的关联特性进行拟合，拟合参数传送到云端，为云计算提供边缘网络的等值参数；紧急情况下，云计算可为全局提供紧急决策支持，缩短故障恢复计算的响应速度。因此，研究建立遵循云边端网络架构约束、按边缘网络划分的电网信息与计算业务，构建云边协同优化模型和交互逻辑是本文的研究突破点。

为此，本文在遵循云边端网络架构的约束条件下，提出了基于边缘网络前置预计算的柔性互联配电网故障恢复优化算法及其云边协同调控逻辑。首先，按网络边缘和故障时刻对变量和约束进行划分，构建了边缘网络前置预计算模型，建立了边缘网络交互功率与自身网络最优潮流指标之间的分段线性关联函数。然后，提出基于边缘网络前置预计算的柔性互联配电网故障恢复优化算法与云边协同调控逻辑，将各边缘及云端的优化模型维度和规模限制在单个网络内。由于各边缘网络的优化计算前置到故障前完成，当配电网发生故障时，相邻边缘网络的运行指标直接由关联函数映射，节省了非故障配电网的计算耗时，提高了故障恢复优化策略的响应速度。最后，构建了多区域柔性互联配电网测试网络，通过配电网潮流核算和算例分析，验证了本文所提方法的准确性和计算效率。

1 柔性互联的ADN 云边协同的故障恢复优化策略

1.1 FID 基本概念和工作原理

FID 是一种新型电力电子设备，可用于取代ADN 中传统的功率不可调节的联络开关，其各端口由电压源换流器（voltage source converter，VSC）组成，连接着不同的配电网馈线区域。同时，不同端口换流器之间通过直流母线耦合，实现各互联配电网间功率的汇聚与分配，其网络拓扑如附录A 图A1所示。

FID 常用的控制模式包括定直流电压/无功功率控制（定Udc/Q控制）、定有功功率/无功功率控制（定P/Q控制），以及孤岛电源模式的定交流电压/频率控制（定Vac/f控制）。在配电网正常运行模式下，FID 通常采用定Udc/Q和定P/Q组合的控制模式，通过调节各区域配电网通过FID 交互的功率，实现配电网潮流优化调整；而在配电网故障恢复的紧急情况下，FID 可将其他相邻ADN 富余的功率用于支撑故障网络，恢复尽可能多的负荷供电。

1.2 柔性互联配电网故障恢复云边协同调控架构

为构建云边协同的统一故障恢复优化模型，需明确各ADN 一致性目标及优化模型的形式。故障恢复优化可视为典型的MISOCP 优化问题。其中，目标函数f按故障边缘网络和非故障边缘网络进行划分，约束条件包括不等式约束、等式约束以及二阶锥约束，如式（1）所示。

式中：ΩADN为柔性互联的相邻非故障ADN 集合；ffault(·) 为故障边缘网络的故障恢复综合指标；fhealth，i(·)为非故障边缘网络ADN-i的运行综合指标；x为优化变量列向量；A、K分别为不等式约束和等式约束下变量的系数矩阵；b、d为约束中的常数列向量；‖ · ‖2为一个二范数，表示锥约束的阶数为二阶；Qk、ak为第k个二阶锥约束下变量的系数矩阵；qk和pk分别为第k个二阶锥约束下的常数列向量和常数；m为二阶锥约束的个数。

为解决MISOCP 模型因规模和维度增加导致的求解速度慢、求解难等问题，需对优化模型进行分块、解耦，限制各分块模型的规模。本文以多端口FID 作为边界，划分ADN 各网络边缘，在各边缘网络层面布置边缘设备，各边缘设备与云端通信，完成数据交互及多个边缘的协调控制，如图1 所示。为提升故障恢复策略的响应速度，本文在云边协同架构的约束下，提出边缘网络前置预计算方法，并部署在边缘设备上。边缘设备仅收集并处理本边缘网络的运行数据，限制优化问题的维度和规模，在ADN正常运行的空闲时间，对网络内收集的信息进行前置预计算处理，结果送至云端。然后，提出基于边缘网络前置预计算的故障恢复优化算法，并将其部署在云端上，若某ADN 发生故障，由云端进行协调优化计算。云边网络协同架构的服务功能及其交互逻辑如图1 所示。

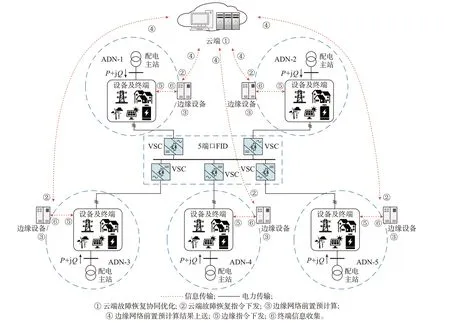
图1 云边网络架构的服务功能及其交互逻辑Fig.1 Service functions and interaction logic of cloud-edge network architecture

在系统正常运行时，各边缘网络均将自身视为非故障网络，按定时触发或阈值触发机制，执行边缘网络前置预计算，随时为云端提供本网络的特征关联拟合数据，以备故障恢复协同优化计算调用。

1.3 边缘网络前置预计算

本文所提边缘网络前置预计算的目的是利用闲时计算资源，拟合计算出FID 交互功率与网络运行综合指标的关联函数，供云端协同优化调用。

考虑到FID 各端口的有功和无功功率可解耦独立控制，各ADN 之间经过FID 的电气量交互仅存在有功交互量，在ADN 网络运行状态变化不大时，其最优潮流的综合指标与FID 交互有功功率可构成具有一定时效性的关联函数。设边缘网络（ADNx）向FID 输入有功功率为，ADN-x的最优运行综合指标与存在隐式关联，定义为Fpre，x()，即式（1）的目标函数中，非故障边缘网络ADN-x的运行综合指标目标函数可替代为Fpre，x()。

在隐式关联Fpre，x()中，计算与每一个对应的Fpre，x()指标值，实际上均为一个最优潮流问题。本文为保持整体优化模型的凸性，采用分段线性函数对Fpre，x()隐函数进行拟合，从而边缘网络（ADN-x）的最优潮流可由分段线性函数Fpre，x()直接等效。

在此基础上，各边缘网络（ADN-x）可将输入FID 的有功功率作为变量，利用ADN-x自身网络内的运行数据，通过优化求解ADN-x的MISOCP 问题得到不同下ADN-x的优化目标值，从而得到分段线性关联函数Fpre，x()各分段点的参数。本文采用定时或阈值触发机制启动前置预计算，如果边缘网络的运行状态值变化超过阈值，或满足定时周期，则边缘网络更新分段线性关联函数的参数。因此，非故障ADN 的关联函数在定时周期内具有时效性。由于前置预计算的信息和约束仅限于边缘网络内部，最优潮流MISOCP 模型的规模和维度均被限制在单一边缘网络内，计算效率和难度很小。

边缘网络前置预计算步骤如下：

1）收集边缘网络（设为ADN-x）实时运行信息，包括开关运行状态、负荷用电需求、DG 出力、储能荷电状态（state of charge，SOC）等实时信息，并对负荷用电需求、DG 出力进行短时预测。

2）根据收集的边缘网络实时运行信息和短时预测数据，对边缘网络前置预计算的MISOCP 模型参数进行实例化设置。

3）在ADN-x向FID 输入有功功率的约束范围内，按等间隔采样原则对进行逐点扫描取值，并对MISOCP 模型进行求解；求解得到各个采样相对应的优化解及其优化目标值Fpre，x()；将各采样及优化目标值以分段线性MISOCP 模型参数表述。

4）边缘网络将前置预计算所得分段线性关联函数Fpre，x()参数上送至云端，存储至云端数据存储中心，供云端启动优化计算时调用。

边缘网络的前置预计算信息交互逻辑如图2所示。

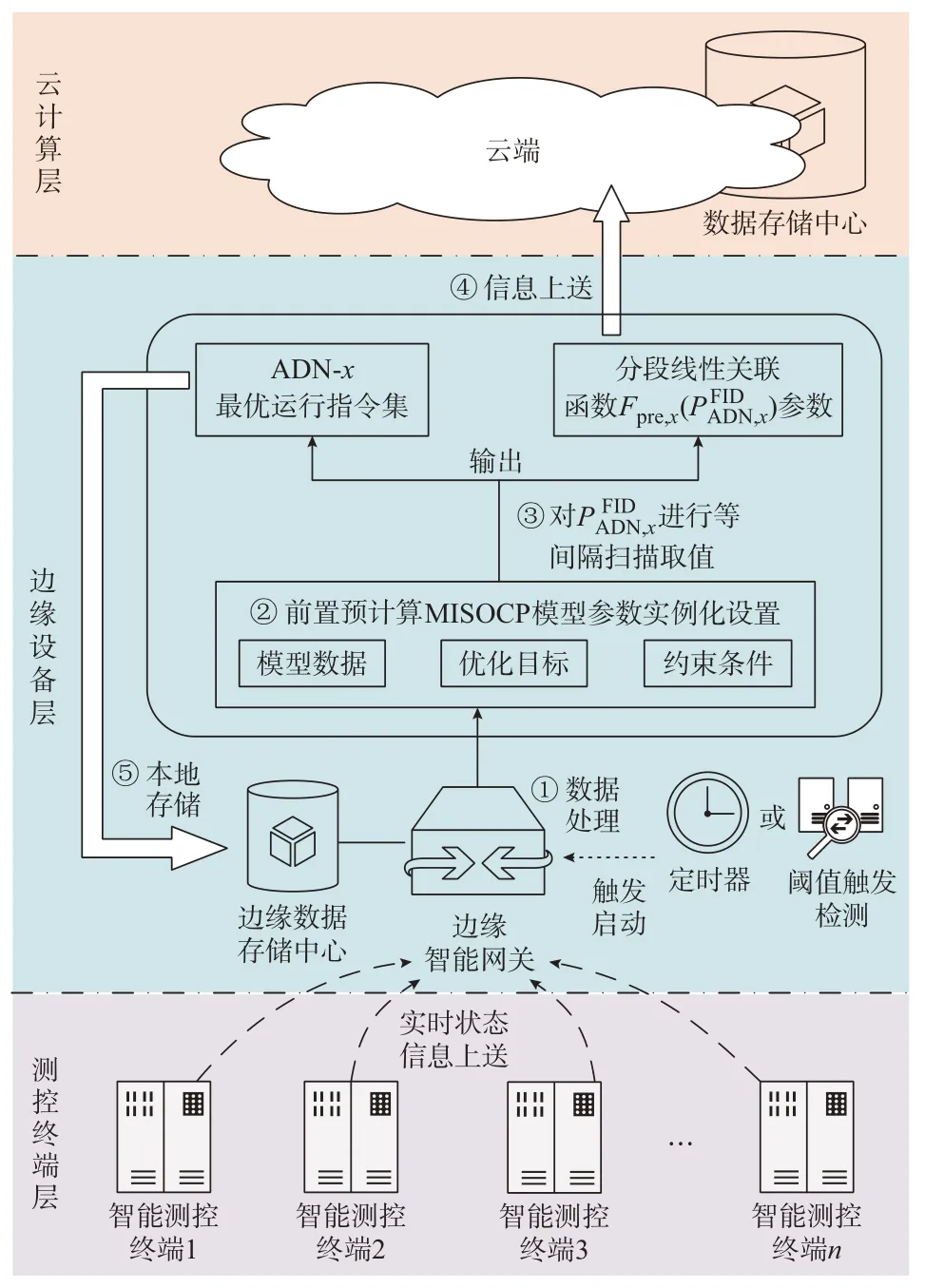
图2 边缘网络前置预计算的信息交互逻辑Fig.2 Information interaction logic for pre-calculation in edge network

1.4 基于边缘网络前置预计算的故障恢复协同优化

当柔性互联ADN 中的任一网络（设为ADN-y）发生短路故障时，在完成故障辨识与定位后，将故障边缘网络的运行信息及故障区段定位信息上送至云端，触发云计算。云端启动故障恢复优化计算。首先，云计算将与故障网络相邻的边缘网络均等值为带Fpre，x()约束的有功功率电源Sx，如附录A图A2 所示；然后，采用分段线性关联函数Fpre，x() 约束来描述ADN-x的最优潮流MISOCP 模型。 由于各相邻边缘网络的Fpre，x()参数已在边缘网络前置预计算时上送到云端，云计算可在云端直接获取Fpre，x()的数据，且Fpre，x()为直接与决策变量相关的目标函数。因此，故障恢复优化模型的信息与约束均被限制在故障边缘网络（ADN-y）内，求解难度大为降低，计算效率也得到大幅度提升。

云端的基于边缘网络前置预计算的故障恢复协同优化计算及其云边协同调控逻辑的步骤如下：

1）云端接收到故障边缘网络（ADN-y）上送的运行数据和故障区段定位信息，启动故障恢复协同优化计算。

2）云端直接调取相邻非故障边缘网络前置预计算的分段线性关联函数参数。

3）云端根据故障边缘网络（ADN-y）的运行数据和相邻边缘网络的分段线性关联函数参数，对故障恢复优化模型进行实例化参数设置及优化求解。求解结果包括：故障网络开关变位、FID、DG、ESS、可控负荷、分组电容器等控制指令值，以及相邻边缘网络输入FID 的有功功率指令。

4）云端将优化计算结果的各项指令下发到故障边缘网络及相邻边缘网络。

5）故障边缘网络（ADN-y）将云端下达的故障恢复调控指令转发至边缘网络内的各智能测控终端。

6）非故障边缘网络根据云端下达的FID 端口的功率调节指令，从各自边缘网络前置预计算的最优控制指令集中，搜索并插值获得各可控设备的最优运行指令值，下发至边缘网络内的各智能测控终端。

由此，本文按照云边端三层网络架构，提出基于边缘网络前置预计算的故障恢复协同优化算法。故障恢复的云边协同调控逻辑如图3 所示。

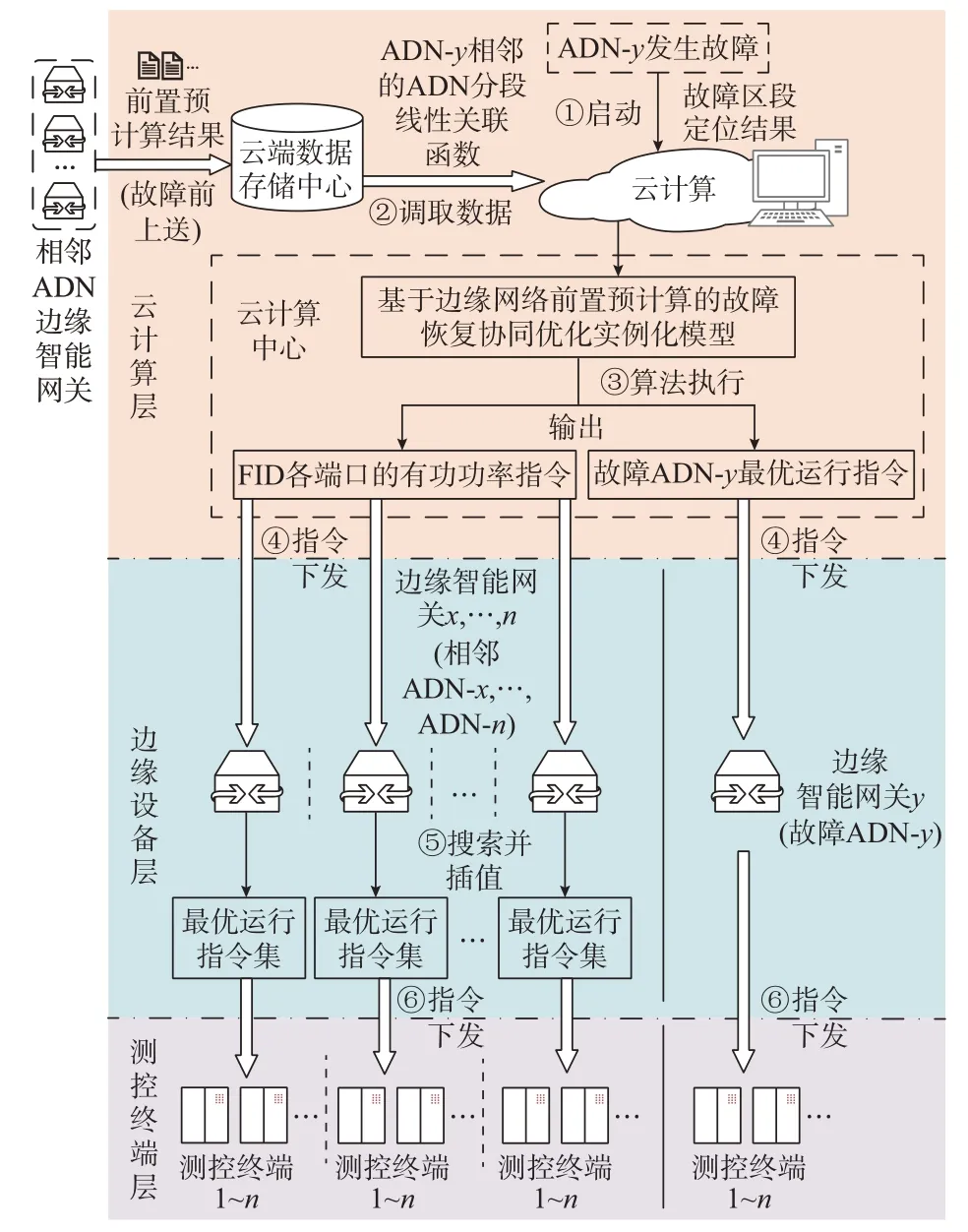
图3 基于边缘网络前置预计算的故障恢复云边协同调控逻辑Fig.3 Cloud-edge collaborative dispatch logic for fault restoration based on pre-calculation in edge network

2 边缘网络前置预计算模型

在式（1）的柔性互联配电网的故障恢复优化中，非故障ADN 的优化计算实际上是在求解ADN 向FID 输入有功功率时的最优潮流MISOCP 问题，边缘网络前置预计算的目的是将这部分优化计算前置到故障前完成。根据1.3 节所述前置预计算策略，在ADN 安全运行约束下，对ADN-x(x∈ΩADN)输入FID 功率(x∈ΩADN)进行扫描及优化求解，即可确定不同下ADN-x可达到的最优目标值。此外，本文的故障恢复问题重点关注故障发生后一段短时间内的供电恢复，因此，采用单个潮流断面建立前置预计算的优化模型。

2.1 前置预计算目标函数

非故障边缘网络在进行前置预计算时，主要考虑在通过FID 向故障网络提供有功支持时，降低网络运行的功率损耗、减少分组电容器（capacitor bank，CB）投切次数；而针对ESS，考虑到配电网在日前已制定ESS 的24 h 充放电计划，即ESS 各时段的SOC 计划已知，本文考虑尽可能减少ESS 因故障恢复紧急策略执行而改变ESS 的SOC 计划所引起的额外成本支出。以ADN-x在执行前置预计算为例，目标函数可表达为：

式中：Ωline为线路集合；ΩFID为FID 接入节点集合；ΩCB为CB 接入节点集合；ΩESS为ESS 接入节点集合；为流过线路ij的电流平方值；Rij为线路ij的电阻；为节点j处FID 端口的有功功率损耗；和分别为节点j处CB 的投运组数变量和初始投运组数；和分别为节点j的ESS 在时段末的SOC 和SOC 计划设定值；λloss、λCB、λESS分别为网络损耗权重、CB 投切次数权重、ESS 的SOC 相对日前SOC 计划值改变量的权重。

上述目标函数Fpre，x()在前置预计算每轮优化完成后的取值，即为ADN-x与该轮计算所取值对应的最优运行指标参数。

2.2 前置预计算约束条件

1）Distflow 潮流约束。潮流约束利用Distflow潮流模型，电压电流功率的关系式（5）通过二阶锥松弛的方式表示。约束方程可表达如下：

式中：Pij和Qij分别为线路ij上流过的有功功率和无功功率；Pj和Qj分别为输入节点j的有功功率和无功功率；Xij为线路ij的电抗；Ωnode为节点集合和分别为输入节点j的DG 有功功率和无功功率；和分别为节点j的ESS 放电功率和充电功率；和分别为输入节点j的FID 有功功率和无功功率；和分别为输入节点j的负荷有功功率和无功功率；为CB 输入节点j的无功功率；和分别为节点i和节点j的电压平方值。

2）节点电压与线路电流约束：

式中：Uj，min和Uj，max分别为节点j电压的最小值和最大值；Iij，max为线路ij电流的最大值。

3）DG 容量约束。DG 实行有功功率的独立决策，同时保证功率因数不能过低。约束方程为：

4）CB 约束：

5）ESS 约束。ESS 的约束主要包括充放电功率约束及储电容量约束。约束方程为：

6）FID 约束

FID 输出功率需满足端口VSC 的容量约束，同时端口存在功率损耗，FID 的有功损耗用二阶锥松弛的方式表示。约束方程可表示为：

综上，前置预计算的优化模型如下：

根据上述模型，边缘网络（ADN-x）在正常运行时，采用定时/阈值启动等模式开启边缘网络前置预计算，分段线性关联函数参数计算结果被上送至云端，供云端启动故障恢复计算时调用。

3 基于边缘网络前置预计算的故障恢复协同优化模型

通过边缘网络前置预计算，各边缘已求得各自ADN 通过扫描得到的不同输入FID 有功功率下的分段线性关联函数参数，且该数据已上送至云端数据存储中心。一旦某个ADN 发生故障，云端立即调取相邻ADN 的前置预计算数据，构建前置预计算分段线性关联函数、故障恢复全局优化目标、故障ADN 约束条件。

3.1 边缘网络前置预计算分段线性关联函数

假设在ADN-x的前置预计算中，扫描点数为n，每一次扫描所取的分别为px，1，px，2，…，px，n，各扫描点对应的ADN-x的MISOCP 问题目标最优值 参 数 分 别 为Fpre，x(px，1)，Fpre，x(px，2)，… ，Fpre，x(px，n)，将逐点依次相连得到分段线性关联函数Fpre，x()。该关联函数的线性规划形式可表达为：

式中：wx，i(i=1，2，…，na)为一组na个的辅助连续变量；zx，i(i=1，2，…，na-1)为一组na-1 个的辅助布尔变量，用来限定wx，i(i=1，2，…，na)的取值，从而和Fpre，x()所在的分段区间可通过wx，i确定。

3.2 故障恢复协同优化目标函数

以ADN-y发生故障为例，设定故障恢复负荷停电损失、线路开关操作次数（包含线路开关和负荷开关）、线路有功损耗、FID 端口的有功损耗、ESS 的SOC 相对计划值的改变量、CB 投切次数加权和最小为目标，并且把相邻非故障边缘网络的前置预计算分段线性关联函数加入目标函数中。目标函数Ffault的表达式为：

式中：fLoad、fLoss、fswitch、fESS、fCB分别为负荷恢复、网络损耗、开关操作次数、ESS 的SOC 相对日前SOC 计划值的改变量、CB 投切次数的目标函数；λload、λswitch分别为对应目标函数的权重系数；Ωunode为不可控负荷节点集合；为节点j的停电负荷量；xj为节点j的带电状态；ωj为节点j负荷的重要度权重；αij和αij，0分别为线路ij的开关状态变量和初始开关状态；βj和βj，0分别为节点j不可控负荷开关的状态变量和初始开关状态。

为了实现优先为重要度较高的负荷恢复供电和尽可能恢复更多的负荷，可设置λload远大于其他目标函数的权重系数，并赋予重要度较高的节点j以较大的权重ωj。

3.3 故障恢复协同优化约束条件

1）故障ADN 的Distflow 潮流约束

故障ADN 在故障恢复网络重构时，线路开关状态会发生改变，因此，其Distflow 潮流模型需要考虑线路开关断开和闭合的情况。引入大M法建立线路潮流与线路开关状态变量αij的关系。同时，建立线路状态变量αij与故障线路信息间的关联，得到如下新增的适用于网络重构的线路潮流与节点电压约束方程。

式中：M是一个较大的正数；Ωfault为故障ADN 的故障线路集合。

2）辐射状与连通性拓扑约束

网络重构和孤岛划分后的ADN 需满足辐射状运行条件，且孤岛内必须含有至少一个具有黑启动能力的DG 或FID 接入节点。

本文新增一个“虚拟0 号节点”，当形成孤岛时，该节点通过“虚拟线路”与孤岛的平衡节点相连，维持着ADN 各带电节点的连通性。同时，引入“虚拟功率”的概念，其由虚拟节点发出，只需保证输入带电节点的虚拟功率比流出的多1 个单位，并且ADN的带电节点数比闭合线路数少1，即可将ADN 约束为辐射状网络。约束方程可表达为：

式中：Ωslack为可充当平衡节点的节点集合；α0，j为虚拟节点与节点j连接的虚拟线路的开合状态；Pˉij为流过线路ij的虚拟功率。

在上述约束方程中，式（24）表示ADN 内至少有1 个节点充当平衡节点；式（25）表示带电节点的虚拟功率约束；式（26）表示带电节点数比闭合线路数少1 的约束方程；式（27）表示线路的开合状态与两端节点带电状态之间的关联性。

3）负荷约束

ADN 的负荷分为可控负荷和不可控负荷。当ADN 发生故障时，可控负荷可根据故障恢复的需要调节自身功率需求，不可控负荷的功率需求无法调节，由故障恢复优化结果决定是否操作负荷开关使其断开。约束方程可表达为：

式中：Ωcnode为可控负荷节点集合；和分别为节点j负荷的最大有功需求和无功需求。

4）其他约束

除上述约束方程外，节点电压与线路电流约束、DG、CB、ESS、FID 约束均与2.2 节前置预计算模型的约束一致。

综上，基于前置预计算的故障恢复协同优化模型如式（30）所示。

根据上述基于边缘网络前置预计算的故障恢复协同优化模型模型，云端根据故障前各边缘网络上送的前置预计算结果数据以及故障边缘网络（ADN-y）的数据，优化求解得到故障边缘网络的最优运行指令集，以及FID 各端口的有功功率指令(x∈ΩADN)，结果被下发至各边缘智能网关。故障边缘网络ADN-y向网内设备终端下发指令；相邻非故障边缘网络ADN-x(x∈ΩADN)根据云端下发的FID 端口的有功功率指令，结合前置预计算结果中的与ADN 输入FID 有功功率相关联的最优运行指令集，搜索并插值求取与对应的各设备的最优运行指令，并下发至相应的设备终端，从而完成柔性互联ADN 的故障恢复。

4 算例分析

4.1 算例参数

为了验证所提方法的有效性与准确性，本文选取的柔性互联配电网算例由5 个ADN 通过1 个FID 互联组成。其中，ADN-1 和ADN-2 的负荷有功、无功功率以及线路参数来源于标准IEEE 33 节点系统，最大安全电压为1.05 p.u.，最小为0.95 p.u.；ADN-3、ADN-4 和ADN-5 的负荷有功、无功功率以及线路参数来源于标准IEEE 69 节点系统，最大安全电压为1.1 p.u.，最小为0.9 p.u.。各ADN 的根节点1 均为平衡节点，其电压固定为1.0 p.u.。在各ADN 中接入DG、ESS、CB；5 个ADN 通过一个5 端口FID 互联，各ADN 的接入点分别为节点18、33、65、65 和65，各ADN 的设备接入点和参数分别如附录A 表A1 所示，算例测试网络结构如图A3 所示。

负荷分为4 类：一类负荷、二类负荷、普通负荷和可调负荷。以ADN-3 为例，这4 类负荷的节点号以及权重系数如附录A 表A2 所示。前置预计算模型和故障恢复优化模型的各项权重系数为：负荷恢复权重λload、网络损耗权重λloss、开关操作次数权重λswitch、ESS 的SOC 相对日前SOC 计划值改变量的权重λESS、CB 投切次数权重λCB，如表A3 所示。本算例选取的故障恢复优化时段范围为1 h。执行优化计算的计算机硬件环境为Intel Core i5-11400 CPU（2.60 GHz），16 GB 内存，优化求解环境采用MATLAB R2019a-YALMIP-gurobi 9.5.1。

为了验证所提方法的准确性与有效性，本文设置ADN 发生故障来模拟故障恢复优化求解。由于所提求解方法包含边缘网络前置预计算和基于边缘网络前置预计算的故障恢复协同优化计算两部分，本文将分别对这两部分计算进行算例分析。

4.2 边缘网络前置预计算

假设在某一整点时刻，各边缘网络ADNx(x∈ΩADN)触发开启前置预计算。根据已预处理过的自身网内的数据配置前置预计算模型，在FID端口容量[-2，2]MV·A 范围内，设定一组n个等间隔输入FID 有功功率数值［px，1，px，2，…，px，n］，并开启前置预计算模型（式（13））的求解。由于FID 端口可传输功率上下限范围为4 MW，为兼顾计算耗时与分段线性函数拟合的精度，本文选取100 个分段点作为本算例前置预计算的分段点数。

通过前置预计算，各边缘网络ADN-x求得自身网络内与［px，1，px，2，…，px，100］对应的最优潮流MISOCP 问 题 优 化 目 标 函 数［Fpre，x(px，1)，Fpre，x(px，2)，…，Fpre，x(px，100)］，以及所有决策变量的优化结果取值。 将前置预计算结果［（px，1，Fpre，x(px，1)） ，（px，2，Fpre，x(px，2)） ，… ，（px，100，Fpre，x(px，100)）］逐点相连，可得到该ADN 输入FID 有功功率与ADN 最优潮流MISOCP 问题最优解之间的分段线性关联函数。该函数所有分段点的综合数据为一个100×2 的二维数组，各边缘网络将该数据结果上送到云端，供云端执行故障恢复协同优化计算时调用。各边缘网络前置预计算结果的分段线性函数曲线如附录A 图A4 所示。

为了验证本文所取的100 个分段点进行前置预计算得到分段线性关联函数曲线的精度，本文以8 000 个分段点下分段线性关联函数曲线作为参考曲线，并分别设置10、50、100、200、400 个分段点进行前置预计算。以ADN-1 为例，其计算耗时、分段线性关联函数曲线均方根相对百分比偏差结果列于表1，ADN-2 至ADN-5 的偏差结果对比列于附录A表A4。可见，采用100 个分段点进行前置预计算可同时兼顾计算耗时与偏差。

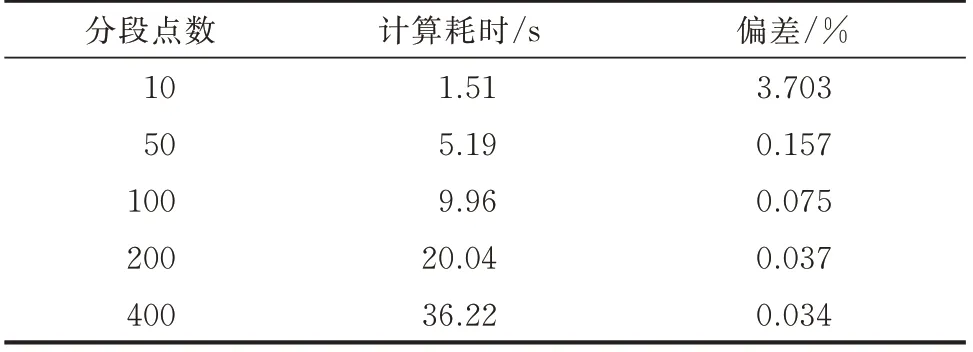
表1 不同分段点数下ADN-1 前置预计算的耗时与偏差Table 1 Time consumption and error of precalculation of ADN-1 under different number of segments

同时，决策变量优化结果中，网内设备部分的变量最优解作为该网络的最优运行指令集，该数据存储在本地边缘网络中，供边缘网络接收云端故障恢复指令时调用。

4.3 基于前置预计算的故障恢复协同优化计算

假设在整点间的时间段内，未触发边缘网络前置预计算的阈值启动模式，则存储在各ADN 边缘和云端的前置预计算结果无须更新。在该整点间的时间段内，设置严重程度不一样的两种故障，分别为ADN-3 的配电主站失压和ADN-3 部分配电线路故障两种场景，作为本算例的分析场景。

4.3.1 ADN-3 的配电主站失压故障

当ADN-3 的配电主站失压后，根节点无法为ADN-3 的负荷提供电压与功率支持，使得ADN-3丢失了2 299.6 kW 的根节点供电功率，ADN-3 网内负荷总功率为3 802.1 kW，网内的DG 和ESS 最大可支撑的有功功率为2 500 kW。采用本文所提基于边缘网络前置预计算的故障恢复协同优化算法进行故障恢复求解。

云端收到ADN-3 边缘上送的故障信息与故障恢复请求后，调取与ADN-3 相邻ADN 边缘的前置预计算分段线性关联函数数据，随即启动故障恢复协同优化模型（式（30））求解，计算得到故障ADN-3的最优运行指令集及FID 各端口有功功率指令。前者发送到故障ADN-3 的边缘执行指令；后者发送到其他非故障ADN 边缘。非故障ADN 边缘则根据云端下达FID 端口的有功功率指令，从前置预计算结果的最优运行指令集中，搜索并插值求取各设备的最优运行指令，从而得到柔性互联配电网故障恢复中所有设备的指令调节方案。

在故障恢复优化求解的所得结果中，各ADN可控设备的功率运行指令调节方案列于附录A 表A5，包括FID 端口输出的有功功率和无功功率、DG输出无功功率、ESS 输出有功功率、CB 投入组数。ADN-3 的开关调节方案、各网间有功功率交互和与之对应的ADN 的最优潮流目标函数值如图4所示。

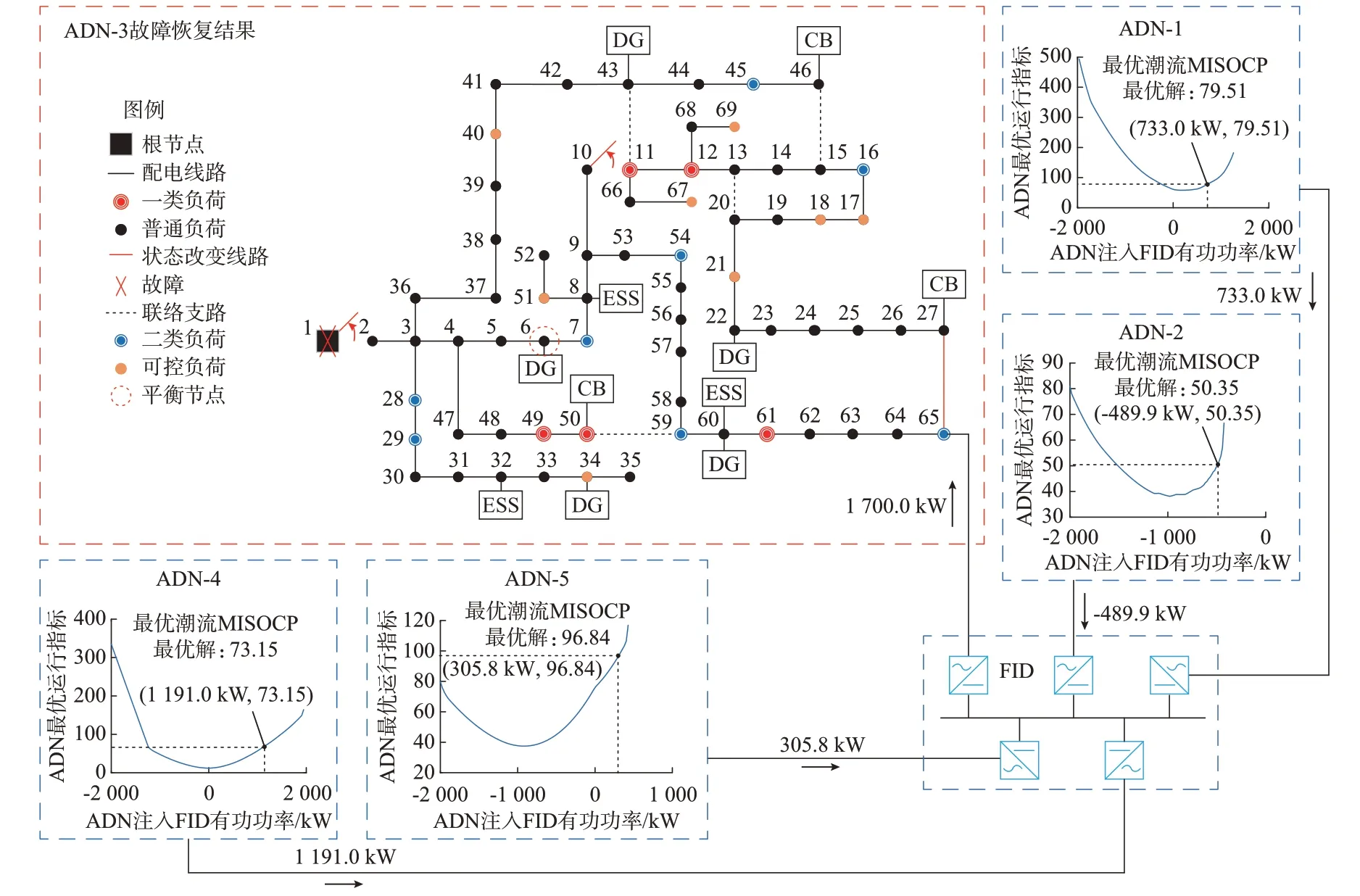
图4 场景1 算例网络故障恢复结果及各网间有功功率交互Fig.4 Results of fault restoration of case network and active power interaction between ADNs in scenario 1

由图4 可见，该场景受故障影响供电的ADN-3的根节点1 与节点2 的线路开关断开。由优化结果可知，所给出的故障恢复方案为：图4 中红色支路27-65 从停运转为投入运行状态，支路10-11 由投运状态转为停运状态。然后，各ADN 可控设备的运行指令按附录A 表A5 的优化结果调节，ADN-3 从FID 上获取了1 700 kW 的有功功率支撑，并由节点6 的DG 切换为定Vac/f控制模式充当孤岛的平衡节点，转为孤岛运行。

方案执行后，故障ADN-3 负荷停电功率为227.0 kW，网络损耗为80.44 kW，CB 动作次数为15 次，开关动作次数为2 次，94.03%的负荷恢复了供电。其中，一类、二类负荷和普通负荷均达到了100%的供电恢复率，可控负荷恢复了37.65%的供电。可见，本文所提方法使得尽可能多的负荷恢复了供电。

此外，为验证配置FID 对故障恢复起到的积极作用，不考虑FID 提供网间功率互济作用，在相同的场景下执行故障恢复优化求解，所得目标函数结果列于附录A 表A6。由表A6 可见，若不考虑FID 提供的网间功率互济作用，仅依靠ADN-3 自身网内的电源及调节设备进行故障恢复优化求解，则负荷停电功率为1 729.3 kW，仅54.52%的负荷恢复了供电。可见，配置FID 能有效扩大故障恢复的复电面积、减小故障的停电范围。

4.3.2 ADN-3 部分配电线路故障

ADN-3 某区域发生灾害或事故导致多条配电线路供电受损，分别为线路3-4、4-5、3-28、4-47，导致下游节点4 至节点35、节点47 至节点69 停电，ADN-3 边缘设备向云端上送故障信息与故障恢复请求，由云端和非故障ADN 边缘求得各可控设备的运行指令调节方案。

在故障恢复优化求解的所得结果中，各ADN中可控设备的功率运行指令调节方案列于附录A表A7，包括FID 端口输出的有功功率和无功功率、DG 输出无功功率、ESS 输出有功功率、CB 投入组数。ADN-3 的开关调节方案、各网间有功功率交互和与之对应的ADN 的最优潮流目标函数值如图5所示。

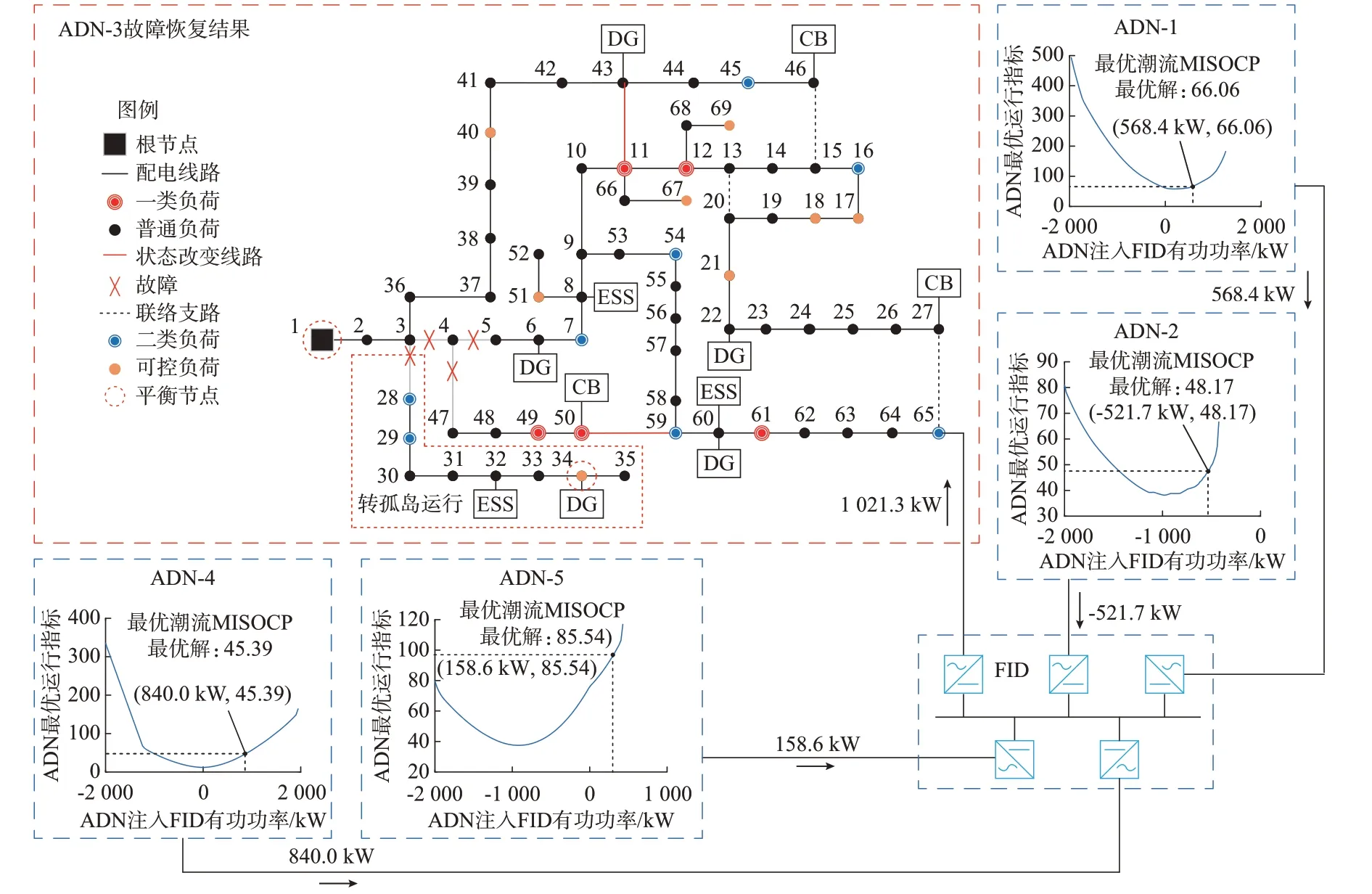
图5 场景2 算例网络故障恢复结果及各网间有功功率交互Fig.5 Results of fault restoration of case network and active power interaction between ADNs in scenario 2

由图5 可见，该场景受故障影响供电的ADN-3的线路3-4、4-5、3-28、4-47 断开。由优化结果可知，所给出的故障恢复方案为：图5 中红色支路11-43 和支路50-59 从停运转为投入运行状态，停电的负荷节点重新与根节点1 建立联系；节点28 至节点35 形成孤岛，节点34 上的DG 切换为定Vac/f控制模式充当孤岛的平衡节点。然后，各ADN 可控设备的运行指令按附录A 表A7 的优化结果调节，ADN-3 从FID 上获取了1 021.3 kW 的有功功率支撑。

方案执行后，故障ADN-3 全部负荷恢复了供电，网络损耗为1 266.6 kW，CB 动作次数为5 次，开关动作次数为2 次。可见，本文所提方法使得尽可能多的负荷恢复了供电。

此外，为了验证配置FID 对故障恢复起到的积极作用，不考虑FID 提供网间功率互济作用，在相同的场景下执行故障恢复优化求解，所得目标函数结果列于附录A 表A8。由表A8 可见，若不考虑FID提供的网间功率互济作用，仅依靠ADN-3 自身网内的电源及调节设备进行故障恢复优化求解，网络损耗为1 657.6 kW，CB 动作次数为12 次，开关动作次数为6 次。可见，配置FID 能有效降低网损、CB 和开关动作次数。

4.4 算法准确度与求解时间验证

为进一步验证本文所提方法的准确度，本文以ADN-3 为故障网络，随机改变ADN-1、ADN-2、ADN-4、ADN-5 的DG 出力，生成400 个算例样本。分别设置4.3 节所述场景1 的ADN-3 配电主站失压、场景2 的ADN-3 部分配电线路故障两种场景，采用本文所提方法对每个算例样本进行前置预计算。然后，执行基于前置预计算的故障恢复协同优化算法，并将所提方法通过基于边缘网络前置预计算的ADN 等值得到的ADN-1、ADN-2、ADN-4、ADN-5 的网络损耗与潮流核算结果进行比较，两者的相对误差与最大误差结果列于表2。其中，相对误差结果为400 个算例样本下两者相对误差的均方根平均值±标准差。由表2 可见，两个场景中本文所提方法与潮流核算结果在各ADN 的相对误差在较低水平，最大相对误差也仅为0.137%，可见所提前置预计算模型精度更高。

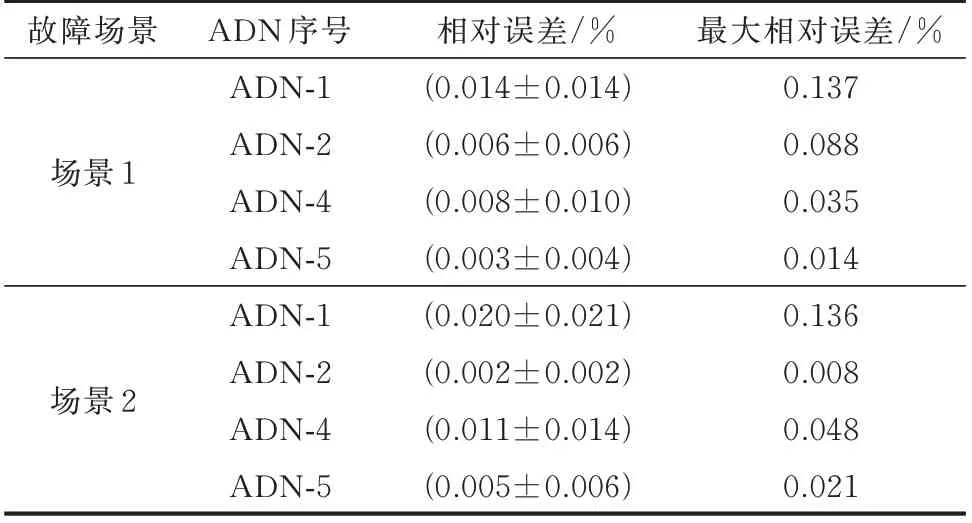
表2 边缘网络前置预计算与潮流核算的相对误差与最大相对误差对比Table 2 Comparison of relative error and the maximum relative error between edge network pre-calculation and power flow calculation

为了验证本文所提基于边缘网络前置预计算的故障恢复协同优化算法对求解响应速度的提升效果，分别采用本文方法和ADMM［31］对上述400 个算例样本进行故障恢复方案的求解，两种方法的求解均在相同的运算环境下进行。两种方法的优化总目标偏差率及其求解时间，分别以附录A 图A5 的散点图和图A6 的柱状图表示。图A6 中，求解时间的均方根平均值与标准差、最大求解时间列于表3。

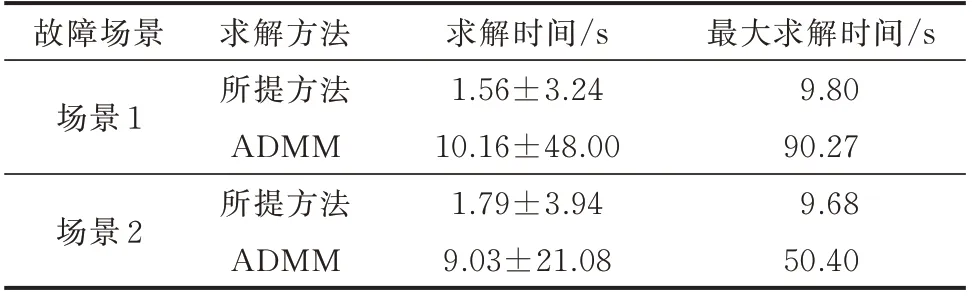
表3 所提方法与ADMM 求解时间与最大求解时间对比Table 3 Comparison of solution time and the maximum solution time between proposed method and ADMM

由附录A 图A5 可见，本文所提方法和ADMM的优化总目标结果差异在400 个算例样本下最大误差均低于1%。可见，所提方法的计算精度与ADMM 一致。由附录A 图A6 和表3 可见，本文所提方法的求解时间在场景1 的400 个算例样本下最大为9.80 s，远小于ADMM 的求解时间最大值90.27 s；本文方法求解时间的均方根平均值与标准差为（1.56±3.24）s，远低于全局求解的（10.16±48.00）s。而在场景2 中，本文所提方法的求解时间在400 个算例样本下最大为9.68 s，远小于ADMM的求解时间最大值50.40 s；本文方法求解时间的均方根平均值与标准差为（1.79±3.94）s，远低于全局求解的（9.03±21.08）s。可见，本文方法的求解避免了ADMM 的多个边缘之间多次优化信息的交互，大大提升了故障恢复优化求解的响应速度。

5 结语

本文在遵循云边端网络架构的约束条件下，提出一种基于边缘网络前置预计算的柔性互联ADN故障恢复优化算法及其云边协同调控逻辑。所提方法按网络边缘和故障时刻对故障恢复的优化变量与约束条件进行划分，将边缘网络前置预计算和故障恢复协同优化模型的维度和规模都限制在单个ADN 内，使得柔性互联ADN 故障恢复优化问题的规模不因互联网络数量增大而增大。同时，通过边缘网络前置预计算节省了故障恢复策略优化计算的计算耗时，提高了故障恢复优化策略的响应速度。通过比对试验与分析，所提前置预计算模型能准确拟合相邻ADN 提供功率支持下的最优运行指标。通过多组算例样本与ADMM 优化结果及耗时对比分析可知，所提方法计算精度与ADMM 一致，且所提方法的求解时间得到明显缩减，大大提升了故障恢复优化求解的响应速度。

此外，本文所提配电网云边协同故障恢复算法依赖于通信网，在台风灾害等通信网破坏条件下有其局限性，后续将进一步研究在通信网故障条件下的配电网故障恢复策略。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。