电动汽车用户参与调控意愿的多代理表征与可信容量量化

马文帅，胡俊杰，房宇轩，吴巨爱，谢东亮，薛禹胜

（1.新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2.南京邮电大学自动化学院、人工智能学院，江苏省 南京市 210023；3.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省 南京市 211106）

0 引言

近年来，电动汽车（electric vehicle，EV）作为一种清洁交通工具得到了迅猛发展，引导EV 有序充放电成为支撑电网安全经济运行的重要手段［1-2］。然而，大多数研究聚焦于EV 优化调度问题，而忽略了EV 用户本身参与调控的意愿。EV 用户是否愿意参与EV 聚合商的调控直接影响到EV 的功率调节能力，EV 用户意愿研究［3-5］成为有序充电技术推广应用的关键问题之一。由于EV 用户的决策行为既不是完全的随机行为，也不完全遵循固定公式，故用户意愿研究是一个难点问题［6］。

目前，EV 用户意愿分析方法主要分为模型驱动法［7-8］和数据驱动法［9］两类。

在模型驱动法的研究中，文献［10］考虑用户参与调控的意愿受各方面因素的影响，建立模糊推理模型对用户意愿程度进行估计。基于模糊规则设置隶属度函数，能够反映不同影响因素对用户的影响，但模糊规则与阈值选取大多取决于研究者的主观理念，缺乏科学的模糊规则制定与阈值选取方法。文献［11-12］建立效用函数评估EV 用户参与调控的意愿，文献［13］建立基于消贾者心理学的用户响应模型，通过比较用户响应度与阈值，判断用户参与调控的意愿。但上述两种方法忽略了用户的非理性行为，对用户意愿的分析过于理想。文献［14］针对充电响应与放电响应分别建立不确定性响应曲线，设置了最大响应率，通过EV 集群总数与响应率判断愿意参与调控的EV 数量。文献［15-16］结合用户的个体行为与社会群体行为对用户参与调控的意愿进行分析，但这种方法仅考虑了价格激励的效果，忽略了其他因素的影响。上述基于模型驱动的用户意愿分析存在两方面的不足：一是以理性人进行决策为依据，而现实中人在决策过程中存在非理性特征；二是模糊规则多基于经验值设定，与实际响应情况可能不符。

基于数据驱动的用户意愿分析可以规避上述模型驱动的缺点。文献［17］从个人属性、车辆属性等方面考虑国内消贾者EV 购买偏好的影响因素，采用混合Logit 定量分析方法分析各类因素对消贾者购置意愿的影响。文献［18］结合大量真实交通运行数据，采用决策树分析了汽车的避让/抢行行为。文献［19］指出，可通过深度学习利用神经网络学习用户的需求侧响应意愿。然而，上述方法存在难以获得大量有效数据的问题。

综上，本文提出了基于小样本数据驱动的EV用户参与调控意愿多代理表征与可信容量量化方法。首先，结合EV 出行行为设计了用户参与调控意愿的调研问卷，采集了真实用户参与调控的意愿数据；其次，通过小样本问卷信息深度挖掘数据关系，建立表征用户集群意愿的多代理模型；然后，提出松弛的用户意愿判别方法，建立考虑用户意愿的可信容量量化模型；最后，通过算例分析了代理个体数等关键参量对EV 用户集群参与调控意愿判别的影响，给出了合理设参时不同置信度下的EV 集群可信容量。

1 问卷设计

在实际的EV 用户充电场景中，用户是否参与调控的决策行为由外部环境的激励和用户自身对于环境变化的感知和反应决定。本文通过问卷的形式，采集不同用户个体对环境的感知与反应的差异性，将外部环境凝练为不同场景下影响用户决策的驱动因素，用答卷者在不同问题上的选择分布来描述用户群体的集体感知与反应。

文献［20］指出，影响EV 参与调控意愿的主要因素包括：EV 入网荷电状态（state of charge，SOC）、停车时长以及充放电电价。然而，仅凭EV入网SOC 无法反映EV 用户出行的里程焦虑情况，需要补充EV 期望离网SOC，综合反映用户的里程焦虑情况。综上，本文选取入网SOC、期望离网SOC、补贴价格及在网时长作为用户是否参与调控的主要影响因素。其中，入网SOC 指EV 接入电网时EV 电池SOC；期望SOC 指EV 用户提车时希望EV 可达到的电量；补贴价格指在EV 用户接受调控时，单位电量可减少支付充电服务贾用；在网时长指单次充电过程中用户EV 接入电网的总时间。入网SOC、期望离网SOC 以及在网时长综合表征了用户出行数据对用户意愿的影响，补贴价格则反映了收益对用户决策行为的影响。同时，在问卷设计时设置了其他影响因素的质询问题，以验证所提出的影响因素是否全面。

1.1 问卷设置

由于不同场景下的用户决策并非保持不变，在具体场景众多的情况下，问卷调查的设计不能简单依赖对全场景的穷举，而应兼顾所有影响因素并设置尽量少的问题数。本文设置两种典型EV 充电行为。行为1：用户在居民小区进行充电直至次日驱车上班；行为2：工作时间在工作场所进行充电，工作期间没有用车计划。在以上两种充电行为下，分别采集EV 用户决策行为数据。

不同因素对用户参与调控的影响不同，随着入网SOC、在网时长与补贴价格增大，用户参与调控的意愿不断提高，直至饱和。期望离网SOC 的影响与上述因素相反。为了表征上述因素对用户参与调控的影响，分别对用户愿意参与调控的入网SOC、期望离网SOC、补贴价格与在网时长的心理阈值进行采集。心理阈值反映了用户接受调控时该影响因素的心理预期边界，当实际运行数据满足用户接受调控的心理预期时，用户愿意接受调控。影响因素对用户决策的影响程度对不同用户有所不同，不同的重要程度反映了用户不同的偏好程度与个体的差异性。在有限数量的问题中，关键因素阈值的调查不能实现用户关键因素偏好的完全覆盖，尤其是当采集到的有效问卷数量有限时。虽然问卷中的每个问题仅与一个因素有关，但整个答题表仍然揭示了一个人对所有因素之间关系的确定性观点。因此，为了体现影响因素的重要程度，设置了重要性排序问题。具体问卷设置如附录A 表A1 所示。

1.2 问卷数据预处理

为了直观地对用户意愿情况进行分析判断，本文对采集的数据信息进行预处理。首先，对影响因素重要程度进行自然数编码，将用户认为的最重要的影响因素编码为“1”，次重要的影响因素编码为“2”，以此类推，形成4 个影响因素的重要性程度序列。然后，对影响因素的心理阈值及EV 实际状态信息进行编码，将问卷选项“A”编码为“1”，选项“B”编码为“2”，以此类推，形成用户不同影响因素心理阈值序列。其中，为了排除用户最大利己原则的影响，针对充电补贴的心理阈值调研采用开放式问题，根据问卷采集的结果分档编码。

2 用户参与调控意愿表征

2.1 用户分类

在问卷“重要性排序与其他因素采集”模块中，设置“当能满足您的以上需求时，您是否愿意参与EV 调控？”的问题。基于该问题采集的问卷结果将用户分为两类：1）绝对不参与调控；2）可能参与调控。第1 类用户表示无论用户意愿影响因素是否满足该用户的心理阈值，该用户都不愿意参与调控；第2 类用户参与调控的意愿与用户心理阈值有关，需进一步建立模型进行表征，2.2 至2.4 节将对此进行详细讨论。为了在用户意愿判别时生成用户类别，基于式（1）、式（2）可得用户类型的概率分布，记为πs(gi)。

式中：Pr(·)表示事件发生的概率；i为用户编号，且i=1，2，…，M，M为总用户数；gi为用户i的类型标识，gi=0 表示用户i为绝对不参与调控的用户类型，gi=1 表示用户i为可能参与调控的用户类型；M0为绝对不参与调控用户数；M1为可能参与调控用户数。

基于用户类型的概率分布可得到用户所属类别：若用户属于第1 类，则该用户不愿意参与调控；若用户属于第2 类，则需进一步分析。

2.2 用户心理行为建模

为了表征第2 类用户参与调控的意愿，建立表征用户集群意愿的多代理模型［21］量化用户心理决策。首先，构建用户意愿影响因素集合如式（3）所示。

式中：F为影响用户参与调控意愿的因素集合；Sarr为EV 入网SOC；Sdep为EV 离网SOC；T为EV 充电时长；p为EV 充电时的补贴价格。

基于问卷调查的问题设置，用户的心理决策用式（4）表示。用户的心理决策可以分为两类：一类是影响因素重要性排序行为；另一类是心理阈值决策行为。其中，影响因素重要性排序行为反映了用户自身对影响因素重要程度的认知，而心理阈值决策行为反映了用户对特定影响因素的接受程度。式（7）为影响因素重要性排序取值范围，且由于用户对影响因素排序具有互斥性，各影响因素重要性排序不重复，如式（8）所示。式（9）为用户意愿心理阈值取值范围，与问卷调查的设置相关。值得注意的是，此处的取值范围为心理阈值的对应编码，而不是影响因素具体的心理阈值。

式中：Ai为用户i的心理决策行为；为用户i影响因素排序决策；为用户i的心理阈值决策；、和分别为用户i对入网SOC、离网SOC、充电时长和补贴价格重要性的排名；和分别为用户i愿意接受调控时，入网SOC、离网SOC、充电时长和补贴价格的心理阈值。

2.3 基于小样本问卷数据的知识提取

考虑到各影响因素之间的相关性，为实现对用户行为偏好的建模，对问卷中各因素重要性排序进行知识提取。第1 重要因素的概率分布如式（10）所示。在第1 重要因素确定的条件下，第2 重要因素的概率分布如式（11）所示。同理，第3 重要因素的概率分布如式（12）所示。由于本文选取的决策因素共4 个，故第3 重要因素确定后，第4 重要因素随之确定，无须单独讨论。基于式（10）至式（12）可得用户重要性排序行为联合概率分布，记为πr()。

式中：αx为重要性排名是x的影响因素，且x∈{1，2，3，4}；fz为影响用户参与调控意愿的因素，z∈{1，2，3，4}；Pr(b|a)为事件a发生条件下事件b发生的概率；mα1=f1为重要性排名第1 的影响因素是f1的样本数目，其他m含义同理。

然而，在某些情况下，单个因素重要性排序事件的频次太低，这意味着向下一层提供的信息并无统计意义，这种情况通常发生在排序的底层。为了解决上述问题，使用近似分布来替换原始的信息，以补偿缺失的信息。替换的设计规则如下：

规则1：如果所选排序的样本数量足够，则对问卷收集的相应数据进行严格的频数统计。

规则2：如果所选排序的样本数不足，即数量小于阈值（本文中设置为8），则忽略因素之间的相关性，直接只用影响因素的独立分布作为联合概率分布。考虑到规则2 一般在较低重要性层采用，对频次计算的准确性影响较小，且尽可能保留了问卷的信息量。

在重要性排序联合概率分布的基础上，进一步建立用户对不同因素心理阈值的联合概率分布［19］。以本文采集到的有效数据中第1 重要和第2 重要影响因素的分布情况为例，说明EV 用户影响因素心理阈值的频数分布关联矩阵。如图1 所示，关联矩阵包括4×4 个子矩阵。子矩阵(ψ，ζ)记录了认为ψ行对应的影响因素为第1 重要、ζ列对应的影响因素为第2 重要的用户对这两个影响因素心理阈值的分布情况。由于用户对元素重要性排序具有互斥性，对角线子矩阵为空矩阵。

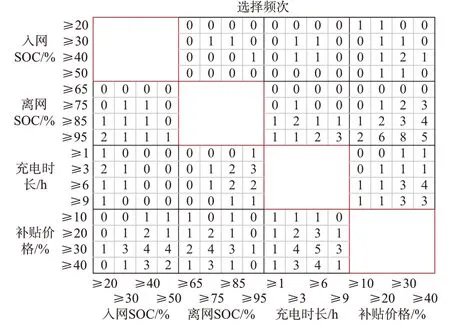
图1 特征因素心理阈值的频数分布关联矩阵Fig.1 Frequency distribution correlation matrix of psychological threshold of characteristic factors

每个子矩阵由影响因素的阈值数量决定。由1.2 节编码规则可知，子矩阵为4×4 的规模。以充电价格为例进行说明，充电价格的心理阈值分为4 个选项，则充电价格代表的子矩阵可被划分为4 行或4 列。在重要性排序已知条件下，用户心理阈值联合概率可用式（15）表示，用户影响因素心理阈值联合概率分布记为。

2.4 第2 类用户意愿判别方法

在真实用户参与调控意愿的判断过程中，无法获得全部用户的心理行为［6］。为了实现用户意愿的判断，需首先生成用于表示真实用户心理行为的代理个体，代理个体心理行为由影响因素的重要性排序与影响因素心理阈值的数据表示。将代理个体对影响因素的重要性排序与影响因素心理阈值的数据作为对应真实用户的心理行为，结合EV 实际运行条件与充电价格等信息判断用户参与调控的意愿。代理个体心理行为数据生成流程如下：

步骤1：依据用户重要性排序行为联合概率分布πr()，采用蒙特卡洛抽样得到用户对影响因素重要性的排序。

步骤2：基于用户影响因素心理阈值联合概率分布πv()，抽样生成不同影响因素心理阈值。

步骤4：判断i是否满足用户集群数量。若满足，多代理生成结束；若不满足，重复步骤1 至步骤3，直至生成的代理个体满足用户集群需求。

第2 类用户意愿判别可以通过式（16）表示。

式中：wi为用户意愿状态，其中，wi=1 表示用户愿意接受调控，wi=0 表示用户不愿意接受调控；为各项影响因素实际值；≥表示EV 各项影响因素实际值均满足该用户接受调控的各项影响心理阈值。

考虑到用户在进行是否参与调控的决策时，各因素并非全部为否决项。以入网SOC 为例进行说明，其他因素类似。当满足入网SOC 为用户认为的重要性最低影响因素的条件时，若EV 的实际入网SOC 低于该用户的心理阈值，则不能对用户参与调控意愿进行完全否定，依据式（16）进行用户意愿判别过于严苛，故对用户愿意参与调控的判定条件进行松弛。松弛后的意愿判别公式如式（17）所示。当各项影响因素实际值均满足该用户接受调控的心理阈值时，用户意愿状态为1；当重要性最低的影响因素实际值不满足用户该项影响因素心理阈值，且低于对应心理阈值不超过2 个挡位时，认为用户存在愿意接受调控的概率。上述第2 种情形下的用户参与调控的意愿服从二项分布，二项分布的参数可根据用户行为习惯调整。其他情况下的用户意愿状态为0。

2.5 用户意愿判别总流程

基于2.1 至2.4 节的内容，用户集群参与调控意愿表征流程如图2 所示。

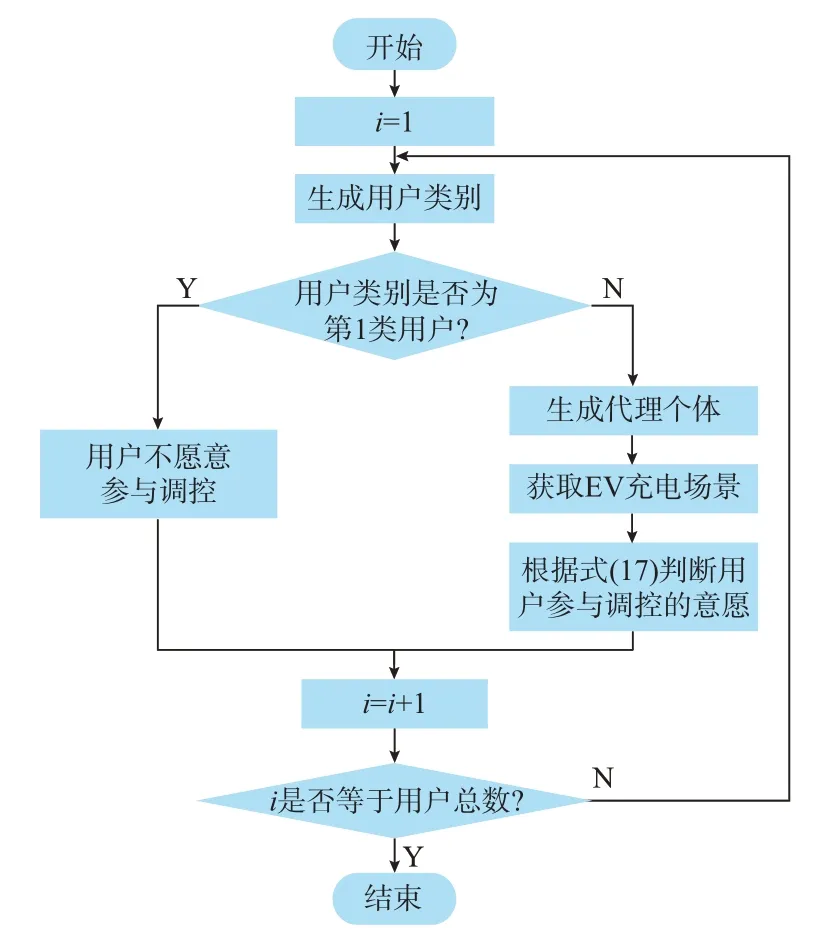
图2 EV 用户参与调控意愿的多代理表征流程图Fig.2 Flow chart of multi-agent representation for willingness of EV users to participate in regulation

具体内容如下：

步骤1：针对用户i，基于用户类型的概率分布πs(gi)生成该用户类别。

步骤2：判断该用户是否为第1 类用户。如果是，则该用户不愿意参与调控；否则，根据2.2 至2.4节内容判断该用户参与调控意愿。

步骤3：更新用户编号，判断是否等于EV 用户集群总数，如果等于则流程结束；如果小于，则重复步骤1 至3。

本文建立的多代理模型可反映开展问卷调查的用户集群心理行为。在实际应用时，需依据不同集群心理决策问卷数据对模型参数进行调整。

3 EV 集群可信容量量化

基于第1、第2 章内容可实现EV 用户参与调控意愿的表征，本章将进一步讨论考虑用户意愿后EV 集群可信容量量化，通过EV 集群可信容量验证本文用户意愿表征方法的合理性。EV 可信容量是指在一定置信度下，实际运行中可以被调度的备用容量。由于本文提出的用户意愿表征方法中，用户代理个体基于概率分布生成，EV 用户意愿具有一定的不确定性，不同回合EV 集群的备用容量会出现上下波动，实际运行时备用容量存在一定的失效风险。因此，本文提出通过置信度量化可信容量。

首先，采用文献［22］中提出的考虑用户意愿的备用容量量化模型，计算出EV 集群在k时段的上备用和下备用，具体模型见附录B。多次求解可形成EV 集群备用容量集合，如式（21）、式（22）所示。

本文定义置信度为σ的可信容量表示不同回合备用容量大于等于该可信容量值的概率大于等于σ，具体形式如式（23）、式（24）所示。

4 算例分析

为了验证本文提出的用户参与调控意愿表征模型的有效性，本章以真实EV 用户提供的问卷信息为基础，进行用户意愿判别仿真，分别分析代理个体数、充电场景数与问卷样本数对用户参与调控意愿表征的影响。最后，基于上述分析量化考虑用户意愿的EV 集群可信容量。

4.1 仿真参数设置

通过社交媒体对中国北京某小区用户开展问卷调查，删除没有使用EV 或没有使用EV 计划的用户问卷结果，收集到有效问卷203 份。有参与调控意愿的问卷为197 份，其中，选择夜间充电的问卷数量为108 份，选择日间充电的问卷数量为89 份。问卷数据分布情况见附录C，问卷数据信度与效度分析见附录D。

由于夜间充电与日间充电两种情况的处理过程一致，本文以夜间充电的行为为例进行后续分析。据2016 年4 月至2017 年4 月在美国开展的全美家用车辆调查结果最新版本数据［23］显示，EV 入网时间与离网时间符合高斯分布。本文设定EV 入网时间服从以17：00 为均值、05：00 为方差的高斯分布；EV 离网时间服从以07：00 为均值、05：00 为方差的高斯分布。该数据符合晚入早出的EV 充电情景。EV 入网SOC 和离网时期望的SOC 分别服从均值为0.4、0.8，方差为0.1 的高斯分布。基于上述概率分布，随机生成500 个充电场景，作为本文用户意愿判别的场景库。基于问卷重要性排序与其他因素采集模块中，“当您认为的最不重要的影响因素不满足您参与调控需求时，您是否愿意参与EV 调控？”采集的数据，得到式（18）中的二项分布参数δ=0.52。

4.2 代理个体数对用户接受调控意愿影响分析

由于EV 用户出行不确定性大，不同的EV 用户在不同充电场景下接受调控的意愿不同。本节分析代理个体数对用户意愿的影响，随机选取确定的充电场景，分别生成包含不同数量代理个体的用户集群来进行意愿分析。为了量化用户集群接受调控意愿的情况，本文定义用户响应比指标如式（25）所示。

式中：c为用户集群编号；χc为用户集群c的用户响应比；Nc，s、Nc，y和Nc，n分别为用户集群c的代理个体总数、愿意参与调控代理个体数和不愿意参与调控代理个体数。

基于108 份问卷数据，提取重要性排序与心理阈值的联合概率分布，依据图2 的流程进行用户意愿判别，包含不同数量代理个体的用户集群用户响应比仿真结果如图3 所示。

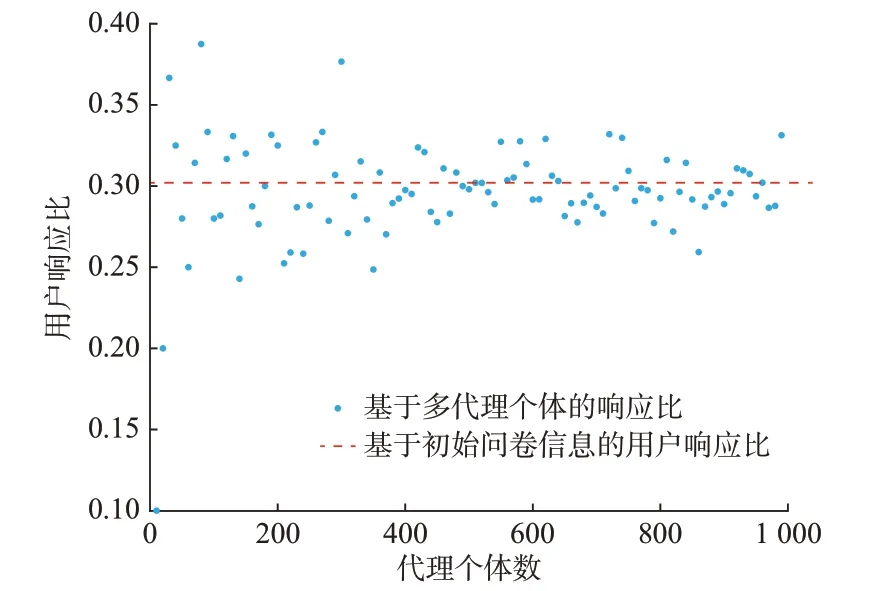
图3 不同代理个体数下的用户响应比Fig.3 Response ratio of users under different number of agents

由图3 可知，代理个体数较少时用户响应比波动较大。这是因为生成代理个体时其心理阈值存在随机性，当代理个体数较少时，不能全面反映用户集群的心理行为。随着代理个体数的增加，用户行为更具有统计学特征，用户响应比逐渐稳定在一个区间。由伯努利大数定律可知，当代理个体数足够大时，用户愿意参与调控的比例即为该充电场景下用户参与调控的概率。这说明通过增大代理个体数可以提高EV 用户参与调控的意愿判别的准确度。

同时，为了验证用户意愿判别方法的有效性，对比分析了基于初始问卷信息的用户响应比结果。如图3 中红色虚线所示，当代理个体数足够大时，基于问卷信息的判别结果与所提模型判别结果具有一致性。

4.3 充电场景规模对用户接受调控意愿影响分析

在相同的充电场景下，4.2 节分析了代理个体数对用户接受调控意愿的影响，但在实际中，EV 用户的充电场景各不相同。为此，本节分析了充电场景规模对EV 用户集群接受调控意愿的影响。将EV充电场景规模设置在［10，500］范围内，以10 为步长增加。为了避免代理个体数的干扰，生成10 000 个代理用户个体，保证可以表征全部用户类型的行为。在每次实验中，从10 000 个代理个体中随机抽取与充电场景数相同的代理个体，进行意愿判别，计算用户响应比。为了抵消随机抽取的偶然性，在相同充电场景规模下重复实验500 次，用户响应比仿真结果如图4 所示。

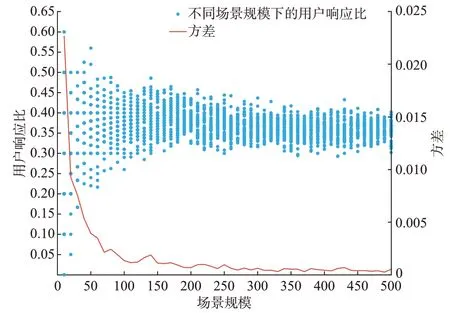
图4 不同充电场景规模下的用户响应比Fig.4 Response ratio of users under different charging scenario scales

由图4 可知，用户响应比在一定范围内波动。这是因为在每次仿真中，每个代理用户个体的心理阈值不同，用户意愿判断结果有所不同，故参与调控响应的用户比例具有波动性，而随着充电场景数的增大，用户响应比波动的范围明显减小。考虑到相同场景规模下多个数据点存在重合情况，为说明用户响应比的分布，计算了用户响应比方差。不同充电场景规模下的用户响应比方差如图4 红色曲线所示。随着充电场景规模的增大，用户响应比方差也明显减小。这说明用户集群意愿随着充电场景规模的增大逐渐收敛。在实际EV 用户意愿判别时，扩大充电场景规模可以有效提高EV 用户参与调控意愿的判别精度。

4.4 问卷样本数对用户接受调控意愿影响分析

除了代理个体数与充电场景规模，用户集群接受调控意愿的准确量化更大程度上受问卷规模影响，本节对不同样本数下的模型预判结果进行比较分析。在每次仿真中，随机选取一定数量问卷样本建立多代理模型，之后基于模型随机生成10 000 个代理个体，在500 个充电场景下判别用户集群愿意参与调控的意愿，计算用户响应比。为了抵消抽取问卷随机性的干扰，重复实验10 次，得到一定问卷样本数下的一组用户响应比数据。问卷样本数设置的范围为［3，108］，以5 为步长增加，结果如图5所示。

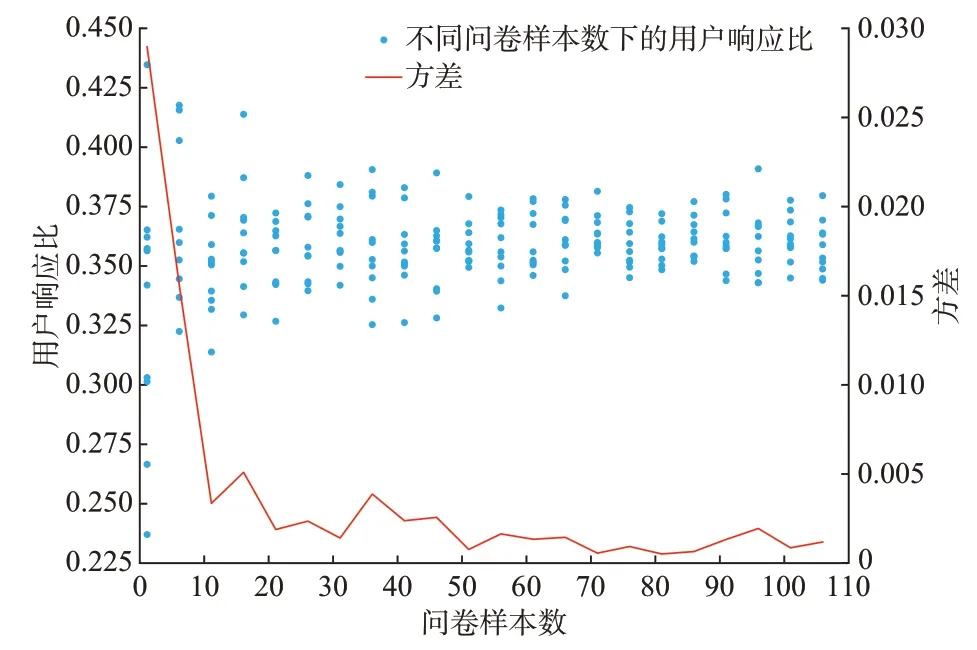
图5 不同问卷样本数下的用户响应比Fig.5 Response ratio of users under different questionnaire sample numbers

在问卷样本数较少时，不同实验回合下用户集群意愿的判别结果波动性较大。随着问卷样本数增加，用户集群意愿的波动范围逐渐收缩，用户集群意愿趋于稳定。这说明问卷样本数直接影响到用户集群意愿判别的准确性。问卷样本数越大，则用户集群意愿判别越准确；反之，则越不精准。由于本文算例中的样本规模仍相对较小，样本数据多样性也有限，用户意愿进入稳定区间的临界问卷样本数相对较小。从图5 所示的用户响应比方差轨迹可知，用户响应比在问卷样本数大于50 份时已趋于稳定。随着问卷样本数量与多样性的增加，用户响应意愿可能收敛到不同的临界值，但收敛性趋势总是成立的。

4.5 用户意愿判别方法有效性验证

4.2 至4.4 节分别分析了代理个体数、充电场景规模以及问卷样本数对用户意愿表征的影响。本节将验证所提松弛用户意愿判别方法的有效性，同时分析充放电调控对用户意愿的影响。

为了验证松弛的用户意愿判别方法的有效性，对比分析了采用松弛方法和非松弛方法下500 名用户调控意愿。如表1 所示，基于松弛的用户意愿判别方法下，用户响应比更接近基于初始问卷信息得到的结果。相比于基于初始问卷信息得到的用户响应比，采用非松弛方法的用户响应比偏低，说明采用非松弛方法会将部分愿意参与调控的用户判别为不愿意，从而导致判别结果存在误差。

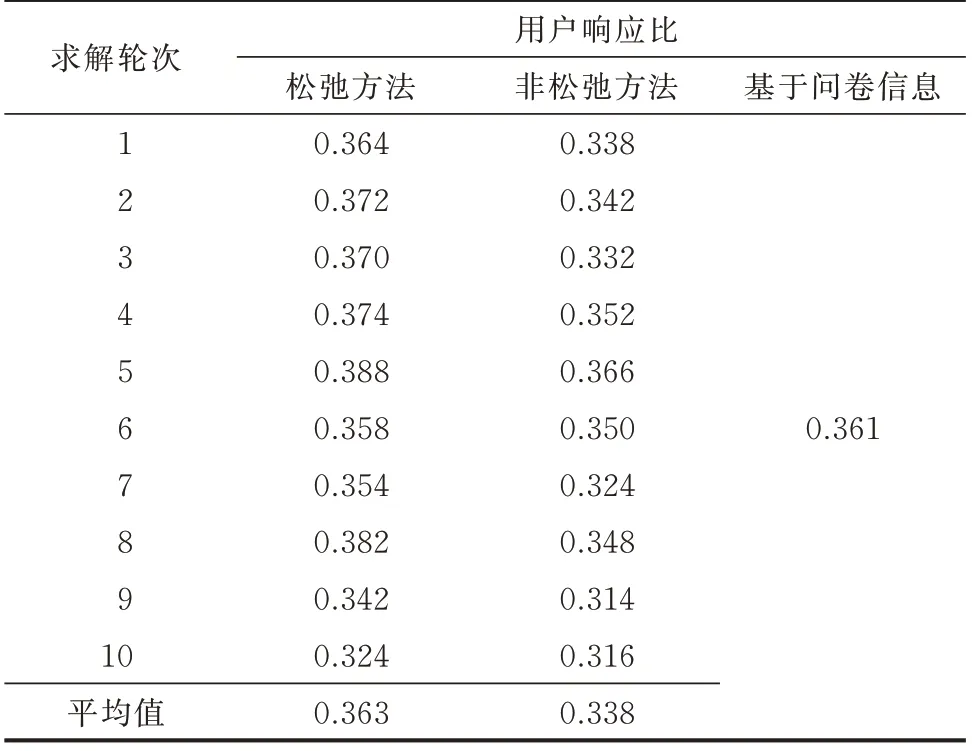
表1 松弛方法和非松弛方法下500 名用户调控意愿对比Table 1 Comparison of regulation willingness of 500 users by relaxation method and non-relaxation method

同时，为了说明参与充电调控与参与充放电调控的差别，本文分别针对只参与充电调控和参与充放电调控的问卷数据建立多代理模型，并对用户集群进行意愿判别，用户响应比如表2 所示。由表2可知，仅参与充电调控时用户愿意接受调控的比例明显高于参与充放电调控的情况。这是因为仅参与充电调控时对用户EV 电池不存在额外损耗，导致用户意愿普遍偏高。

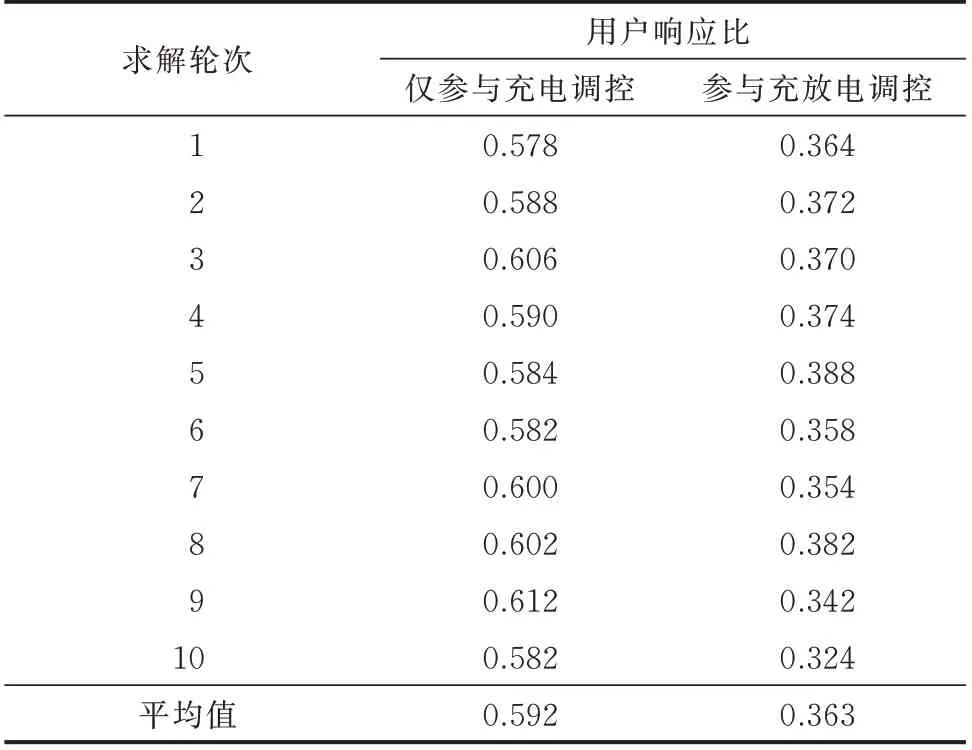
表2 参与充电调控和参与充放电调控不同场景下500 名用户调控意愿对比Table 2 Comparison of regulation willingness of 500 users in different scenarios of charging regulation and charging-discharging regulation

4.6 可信容量量化分析

基于用户意愿判别结果，进一步量化EV 集群的可信容量。本节对包含100 名EV 用户的EV 集群可信容量进行量化分析。其中，EV 电池容量仿真参数设置为50 kW·h，充放电功率上限为7 kW，多时间尺度不同置信度EV 集群可信容量仿真结果如图6 所示。

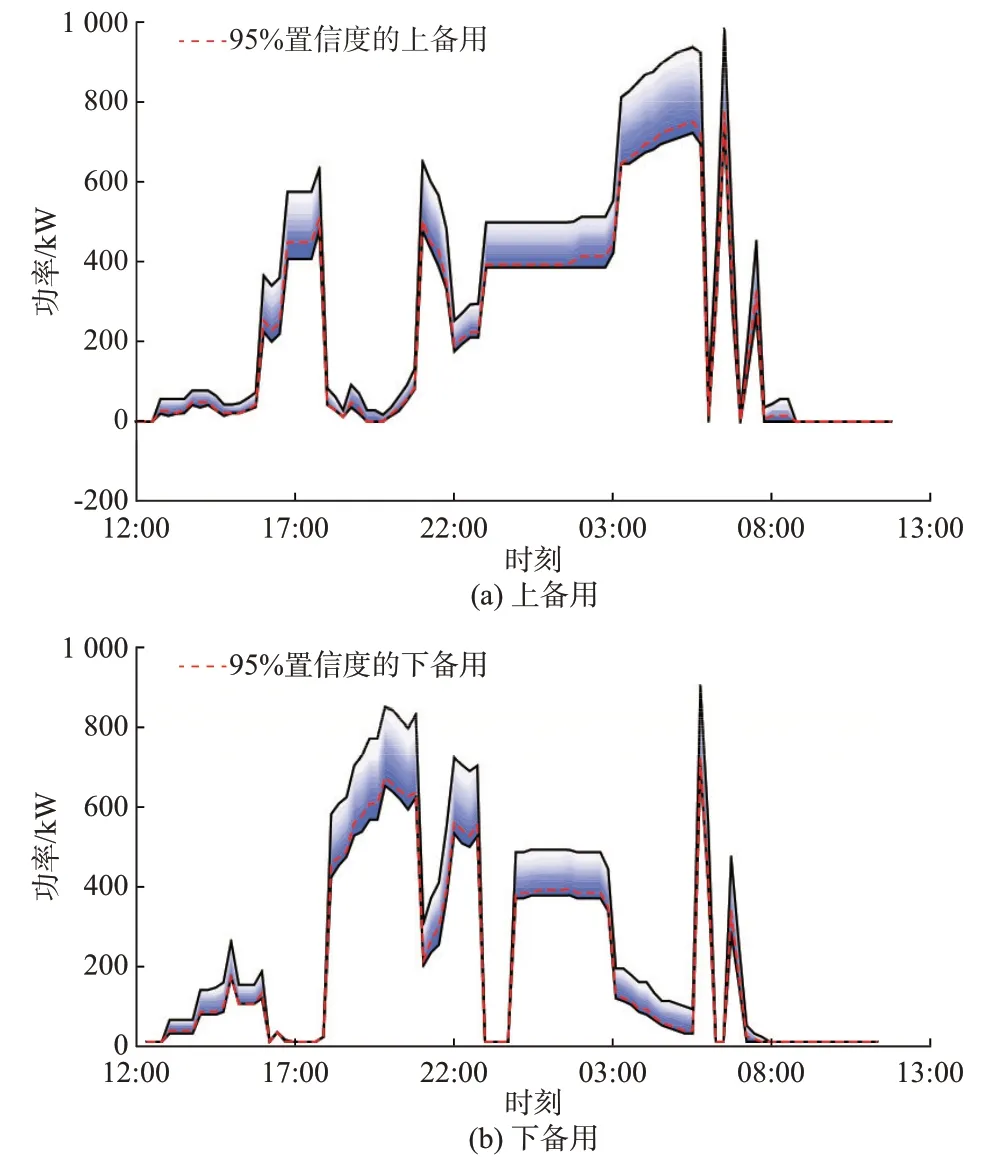
图6 EV 集群可信容量Fig.6 Reliable reserve capacity of EV cluster

如图6 所示，可信容量在一定区间范围内变化。区间内颜色越浅表示该容量的置信度越低，颜色越深表示该容量的置信度越高。考虑用户意愿时不同仿真回合计算的备用容量不同，可信备用容量分布在备用容量上下限之内，可信备用容量值越小则置信度越高。图6 中的红色虚线表示置信度为95%时的可信容量，该数据可以为EV 聚合商参与市场提供参考，兼顾了科学严谨性与工程实用性。

5 结语

本文提出了基于小样本数据驱动的用户参与调控意愿的判别方法。通过算例分析，可得如下结论：

1）本文提出的用户参与调控意愿的多代理模型，通过较少量用户意愿数据的采集与知识提取，可以有效表征更大规模用户集群的心理意愿，在兼顾用户非理性行为的同时，有利于节省大量真实用户参与调研的时间与人力成本，提高有限资源下用户意愿判断的准确性。

2）随着代理个体数、充电场景规模与问卷样本数的增大，用户参与调控意愿判别的随机性与波动性将快速降低，用户意愿判断的准确度由此得以保证。同时，多代理模型易扩容，一定程度上弥补了问卷数量有限的不足，能用于复杂多样的调度场景的判别，适合应对较大规模EV 用户集群在复杂调控场景下的建模需求。

3）由于用户意愿的本质不确定性，EV 集群可信容量的估计存在置信带。本文给出的EV 集群可信备用容量的置信度表达方法，能够明确给出一定置信度下的可信备用容量，兼顾了科学严谨性与工程实用性。

EV 可信备用容量量化技术有望为电网调度部门、EV 聚合商等多主体优化需求侧响应资源、防控电网运行风险、扩大电力市场参与、实现节能减排提供有价值的决策工具。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。