考虑风速不确定性的风电场暂态有功支撑能力在线评估方法

董 昱，孙荣富，丁 然，冯帅帅，起 盼，吴林林

（1.国家电网有限公司国家电力调度控制中心，北京市 100031；2.国网冀北电力有限公司，北京市 100054；3.武汉大学电气与自动化学院，湖北省 武汉市 430072；4.国网冀北电力有限公司电力科学研究院，北京市 100045）

0 引言

风电大规模并网给电力系统频率稳定控制带来了极大挑战，逆变器并网电源大规模并网会造成电网惯量与一次调频能力降低［1-3］，大扰动后的系统频率稳定问题突出。由此，要求风电具备主动参与电网频率支撑的能力是必要的［4］。目前，风电参与调频的方式主要包括备用功率控制与转子动能控制两大类［5］。备用功率控制要求风电在正常运行状态下减载运行，能够提供持续的有功支撑，但经济性较差。转子动能控制则通过短暂释放转子储存动能为电网提供有功支撑，经济性较优。事实上，电网受扰后的频率响应过程包括惯量响应、一次调频等几个阶段。其中，惯量响应阶段内常规机组一次调频尚处于启动阶段，难以提供可观有功支撑，尤其对于高比例新能源接入的低惯量系统，系统频率在该阶段可能会快速跌落。因此，在电网受扰后的惯量响应阶段（后简称惯量响应阶段）内，通过风电释放转子动能以提供快速有功支撑，对抑制系统频率快速跌落具有显著意义。如文献［6-7］设计了基于风机转子动能控制理论的一次调频策略。

除风机控制方案设计外，电网侧整定紧急频率控制策略时，还需明确各场站暂态有功支撑能力，以协同调控多场站资源。对应地，不仅要明确惯量响应阶段内风电场的最大有功支撑能力，还需风电场给定相对应的控制方案及控制指令。在调控能力评估方面，部分文献以调频能量的形式描述其理论有功支撑水平，具体地，基于转速安全限值计算转子可释放动能的理论结果［8-10］。然而，相关文献均未给出明确的控制策略及对应的风机有功响应动态，评估结果不够具体，难以量化对惯量响应阶段内系统频率变化的影响。而且部分研究未能全面考虑风机自身安全要求［9-10］，如转子转速、转矩以及输出功率等均受到严格的安全限制［11-12］。

因此，本文旨在提出一种风电场快速有功支撑方案，并进一步整定控制指令使风电场在惯量响应阶段内能够提供最大暂态有功支撑。具体地，基于控制结构建立考虑风电安全约束的控制指令优化模型，对暂态有功支撑能力进行求解。其中，需要模拟调节过程中风机转子转速、转矩及输出功率的响应动态，以判断给定指令是否满足风机安全运行条件。鉴于机电仿真模拟方法耗时等缺点，部分文献提出建立风机等值模型［6，13］，然后以非解析数值积分方式对上述变量按时序迭代计算。然而，在优化模型中嵌入需要非解析迭代求解的非线性约束条件，将导致采用梯度下降、启发式及人工智能搜索等方式难以保证模型求解速度与解的质量［14-15］。

除此之外，基于预测风速评估场站未来短期调控能力，有益于电网侧控制方案的预决策。其中，考虑预测误差对评估结果的影响是必要的，其建模方法主要分为：基于特定分布形式的预测误差建模和基于非参数估计的误差建模。前者假定误差分布符合特定形式，对模型参数进行估计，解析性较好，但会忽略部分原始数据信息［16-18］。后者不拘泥特定分布形式，可更全面且更准确地囊括原始信息，但解析性较差［19-20］。为保证准确性，本文考虑采用后者进行误差建模，并将其嵌入上述优化模型。然而，其非解析性质将大大降低优化模型求解效率，而求解效率决定评估周期并进一步影响结果准确性。因此，如何实现模型的高效求解是一项关键问题。

针对上述问题，本文面向低惯量系统在惯量响应阶段对快速有功支撑的迫切需求，首先提出了一种简单有效的风电快速频率支撑方案，并全面考虑风电安全约束，构建了以最大化风电暂态有功支撑能力为目标的风电控制指令优化模型；进一步，提出采用差分离散化等方法将模型转化为混合整数线性规划（MILP）问题进行高效求解，以满足在线评估需求。同时，针对未来短期风电场暂态有功支撑能力评估问题，提出采用核密度估计方法进行误差建模，采用拉丁超立方抽样进行场景生成，基于场景法对前述优化问题进行拓展与求解。最后，以某一实际风电场为例，验证了所提方法的快速性与有效性。

1 基于转子动能控制的风机有功调控策略

本文主要对电网受扰后惯量响应阶段（秒级时间尺度）内风电场的暂态有功支撑能力进行评估，因此，可忽略风机模型中部分电磁尺度环节的影响，对风机有功调控模型进行简化［1，13］。以双馈风机为例，其结构如图1 所示。图中：Pm为风机机械功率；Pe、Pe0、ΔPe分别为输出功率及其初值和调整量；PN为额定功率；ω、Δω、ω0、ωref、ωmax分别为桨叶角速度及其变化量、初值、参考指令值、安全上限，由于风机桨叶与发电机转子通过齿轮箱连接，二者转速呈比例关系，因此，后续均以桨叶角速度为代表进行描述；Hw为风机多质量块惯性常数；PI 表示比例-积分环节；β、βmax、βref分别为桨距角及其最大限值、参考指令值，当风机转速超过最大转速或输出功率超出额定功率（βref＞0）时将启动桨距角调节；ΔPadd为附加的有功功率调控指令；脉宽调制（PWM）过程被近似为时间常数Tw很小的一阶惯性环节；Tβ为桨距角控制环节的时间常数；s为拉普拉斯算子；fw(ω，β)表示机械功率关于桨叶角速度与桨距角的函数，其非线性关系如式（1）所示［21］。

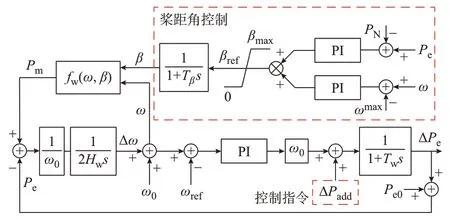
图1 双馈风机的有功功率调整结构Fig.1 Structure of active power regulation for doublyfed wind turbines

式中：ρ为空气密度；A为叶片扫掠面积；vm为风速；Cp为风能利用系数；R为风轮半径；λm为与叶尖速比λ相关的中间变量。

本文所提方案通过在转矩控制环节后附加控制指令ΔPadd实现有功快速调控（完成调控后指令逐渐调节至0），从本质上讲，在惯量响应阶段内利用风电提供快速有功支撑，相当于在该阶段增大了电网的等效惯量。图1 中桨叶角速度参考值ωref在部分转速控制策略下仅与实际风速有关［22-23］。因此，本文近似认为在风机进行暂态有功调控过程中ωref保持恒定。相较于改变风机稳态运行点的超速备用方式，该方案不影响风机正常运行，经济性好且调节速度较快，更适用于电网暂态有功支撑。值得一提的是，该处采用开环控制方案主要是为了便于计算风机暂态有功支撑能力，同时也便于执行电网侧指令以实现快速功率响应，而实际也可在ΔPadd接口处引入频率反馈控制［6］。考虑风电功率反调可能引起的电网频率二次跌落问题，可在调控后期引入转速恢复控制以抑制/缓解功率反调的影响［12］，本文不再赘述。

风机正常运行状态下，施加控制指令ΔPadd（正值）将使得其输出功率快速增大，进而导致桨叶角速度降低，而由于存在桨叶角速度偏差控制（见图1），风机只能短暂释放转子动能，一段时间后桨叶角速度与输出功率将逐渐恢复至初值，但短时间内的快速功率支撑对于抑制频率快速跌落将具有重要意义。为模拟不同控制指令下风机功率及桨叶角速度的响应动态，首先将图1 转化为如式（2）所示的状态空间模型形式［24］：

式中：u表示系统输入，对应图1 中控制指令ΔPadd；x表示状态变量，即传递函数对应微分方程组中可微分变量，包括Δω等；y表示输出变量；f(·)表示状态方程组；g(·)表示代数方程组。

值得注意的是，由于式（1）机械功率计算等非线性环节的存在，式（2）模型整体呈非线性。基于式（2）状态空间模型，可采用梯形积分和牛顿迭代的方式［25］，基于各变量初值计算下一个时刻的变量取值不断迭代，直至达到所需关注动态过程的时长。

2 风电场暂态有功支撑能力优化模型的构建与简化求解

2.1 暂态有功支撑能力优化模型的构建

基于图1 控制策略，本文以惯量响应阶段内风电场能够提供的最大有功调整量（平均功率）作为其暂态有功支撑能力。在有功功率上调过程中，风机转子侧机械转矩低于电磁转矩，导致桨叶角速度在初始阶段降低。除此之外，风机最大电磁转矩限制以及转子侧逆变器容量限制均需要被考虑［11-12］。因此，以风电场在控制指令ΔPadd（待决策变量）下发后最大化0 至th时段内平均有功功率调整量为目标，考虑桨叶角速度安全约束、最大转矩约束以及转子侧逆变器容量约束，建立风电场暂态有功支撑能力优化模型，具体如下：

式中：t∈[0，ts]，其中，ts表示功率动态调整持续总时长；th为电网受扰后惯量响应阶段持续时间；ωmin为桨叶角速度安全下限；Te(t)和分别为t时刻电磁转矩及其安全上限；Qr0为初始状态下风机转子侧无功功率；Pr(t)为t时刻转子侧输出的有功功率；为逆变器容量。

电磁转矩Te以及转子侧有功功率Pr与风电输出功率Pe及桨叶角速度ω有关，其关系可由风机详细数学模型推导得到［6］，即

式中：ωn为同步转速。

事实上，式（4）—式（6）涉及的时序变量（如ω(t)、ΔPe(t)）等难以直接获取，需要在给定ΔPadd的前提下，基于式（2）进行数值积分计算得到。若采用传统方法求解上述包含非线性与非解析计算过程的优化模型，需要在每一次对决策变量迭代寻优的过程中，基于决策变量结果，再次迭代计算目标函数与约束条件。其主要存在如下几个问题：1）每次外层迭代寻优过程均内嵌了关于约束条件的内层迭代计算，极大增加了模型复杂度；2）内层约束条件迭代计算的非解析性质决定了其难以为外层迭代寻优提供梯度信息，恶化了模型收敛性与解的质量。

然而，风电场的暂态有功支撑能力可能随环境因素及其运行状态改变。因此，对模型求解效率提出了较高的要求。鉴于优化模型在上述传统求解模式下的高复杂度与低收敛性，本文提出将约束条件中时序变量的迭代计算过程与模型决策变量的优化搜索过程统一处理，最终将上述优化问题转化为具有成熟规模化处理方法的MILP 问题并进行求解［26］。

2.2 模型简化

2.2.1 模型的差分离散化处理

约束条件中时序变量的迭代计算是由图1 中的传递函数模块导致的。因此，对其中传递函数模块进行差分离散化处理，并将差分离散化所得的各个时刻变量均增补为优化模型的待决策变量，将对应的差分方程及代数方程作为各决策变量间的等式约束，与式（4）的不等式约束共同构成简化后模型的约束集合。以图1 中的转子运动方程为例，首先，利用双线性变换将其转化为如下离散传递函数模型［27］：

式中：F(s)与G(z)分别表示对应的连续与离散传递函数模型；ΔPw表示作用于风机转子上的不平衡功率；T为离散时间步长。

进一步列写对应的时域差分方程，即

式中：α=T/(4Hwω0)；Δω(k)表示k时刻的桨叶角速度变化量表示向上取整）。

可见，变量在k时刻的取值可由k时刻及前向时刻的变量取值线性加权求和得到。同理，在每个时刻均存在如式（8）所示的线性等式，展开如下：

将式中Δω(0)至Δω(Nt)及ΔPw(0)至ΔPw(Nt)均增补为待决策变量，并将上述Nt个方程作为这些变量间的线性等式约束。同理，对图1 中的其他传递函数也作同样处理，最终通过在原模型中增补变量与约束的形式消除了非解析的迭代过程。

图1 中除传递函数模块外，还包括代数计算部分，如式（1）的计算以及其他线性加和项等，同样可将各时刻的变量增补为待决策变量，根据代数方程形成对应的等式约束，以式（1）为例可得：

对于特殊代数计算部分，如图1 中关于桨距角的非线性限幅环节，可以通过大M法将其等效转化为对应的线性不等式组，最终也将被增补为新的约束条件［26］，此处不再赘述。最终，通过上述差分离散化处理，增补优化模型的待决策变量和约束条件，与式（4）共同构成简化后优化模型的约束集合。需要说明的是，经离散化处理后，式（3）目标函数的积分项也对应转化为了线性求和项。

2.2.2 模型的分段线性化处理

优化模型中的非线性项主要包括式（1）、式（5）与式（6），并且非线性主导因素均为在暂态调节过程中随时间变化的桨叶角速度ω(t)。因此，本文首先基于分段线性化理论对桨叶角速度ω(t)分区间处理，如图2 所示，具体如下。

图2 关于桨叶角速度的分段化处理Fig.2 Segmentation of blade angular velocity

考虑ω(t)的变化范围（如[ωmin，ωmax]），引入Npc个分段点ωpc，1至ωpc，Npc，将该区间分为Npc-1 段，则ω(t)必定落在上述区间中的一个。此处，引入0-1型整数变量zpc，i(t)(i=1，2，…，Npc-1)，表征ω(t)的取值是否落在对应的区间内，如zpc，1(t)=1 表示ω(t)的取值落在区间[ωpc，1，ωpc，2)。进一步引入非负实数变量μpc，j(t)(j=1，2，…，Npc)，则可将ω(t)等效表述为：

式（11）表明：根据ω(t)的取值可确定zpc，i(t)，进而ω(t)可被表述为各个区间分段点加权求和的形式，且加权系数μpc，j(t)也可确定。基于式（11），式（1）、式（5）与式（6）可被进一步线性化。

函数Pm=fw(ω，β)具有非线性特征，其中，Pm的变化由ω与β两部分引起。因此，分别考虑两部分的影响对Pm进行线性计算。首先，考虑β=0 的情况，依据=fw(ω，β=0)曲线，计算ω在各个区间分段点ωpc，1至ωpc，Npc取值时的对应取值，记作至。根据式（11）分段线性化原理，P^m(t)可近似线性表达为：

考虑桨距角β在一定范围内变化对风机机械功率的影响近似呈线性［28］，可根据Pm关于β的偏导数近似量化β的变化对Pm的影响，最终Pm(t)可近似线性表达为：

其中，偏导数∂Pm/∂β由式（1）计算，为已知量；Δβ表示桨距角变化量。

结合式（11）对ω(t)的分段化处理，可对非线性约束式（6）进行分段线性放缩。基于式（4），式（6）可被表述为：

进一步，基于大M法，将上式等效转化为Npc-1 组线性不等式：

式中：i=1，2，…，Npc-1；M为取值足够大的常数。

对于式（5）关于转矩安全的约束，同样按照上述方式将其表达为线性不等式约束的形式，本文不再赘述。值得一提的是，在t∈[0，ts]各个时间断面上均存在如式（11）、式（13）及式（16）所示的线性等式/不等式组。最终，将上述各时间断面的线性等式/不等式组纳入上述简化后优化模型的约束集合。

综上，通过上述差分离散化与分段线性化处理，将式（3）和式（4）的模型转化为标准的MILP 问题，并采用Cplex 求解器等软件进行高效求解。

3 考虑风速预测误差的风电场未来短期暂态有功支撑能力计算

3.1 环境风速变化对暂态有功支撑能力的影响

事实上，对风电场的暂态能力评估不应局限于当前状态，其未来短期可调能力的评估结果将有助于电网面向预想事故场景对系统频率控制方案进行预决策，而风速变化是影响风电场暂态有功支撑能力的重要因素。不同风速环境下，风机正常运行时的桨叶角速度及输出功率为：

式中：λopt为最优叶尖速比；ωopt与分别为风速为vm场景下风机正常状态的桨叶角速度以及对应的最大风能利用系数；Pmppt为风速为vm场景下风机正常状态的运行功率。

可见，正常运行状态下，桨叶角速度与风速成正比、运行功率与风速的3 次方成正比。考虑式（4）所示的风机转速及功率约束，风机初始转速与初始功率决定了其可调裕度。除此之外，风速的不同会造成风电场在有功调整过程中机械功率跟随转速的动态变化过程存在差异，进而导致风电场有功功率/桨叶角速度关于控制指令的响应特性存在差异。

因此，风电场区域内风速预测结果对于其未来短期暂态有功支撑能力评估是必要的。然而，目前风速预测误差是客观存在且难以避免的，为提升评估准确性，本文提出根据历史数据对风速预测误差进行统计与建模。

3.2 风速预测误差建模与场景抽样

首先，根据预测风速等级对风电场历史预测风速进行分箱，并根据预测风速对应的实际风速，统计每个分箱内的风速预测误差分布特性。考虑核密度估计这种非参数估计方法良好的泛用性及准确性，本文提出采用核密度估计方法计算各分箱内风速预测误差的概率密度函数。核密度估计的原理为：在每个统计样本处叠加一个核函数，以此来逼近整体的概率分布，本文采用正态分布的概率密度函数作为核函数，核密度估计过程如下：

式中：Nsp为样本数量；Δvm为实际风速预测误差；为第p个样本对应的风速预测误差；σ为正态分布参数；gkn，p(·)为第p个样本对应的核函数；fkn(Δvm)表示核密度估计所得风速预测误差的概率密度函数，进一步计算风速预测误差对应的累计概率分布函数，记作Fkn(Δvm)。

进一步，本文提出采用广泛应用于场景抽样的拉丁超立方抽样方法，基于预测误差的概率分布特性，抽取一组具有代表性的样本代替繁杂的历史数据，原理如图3 所示。

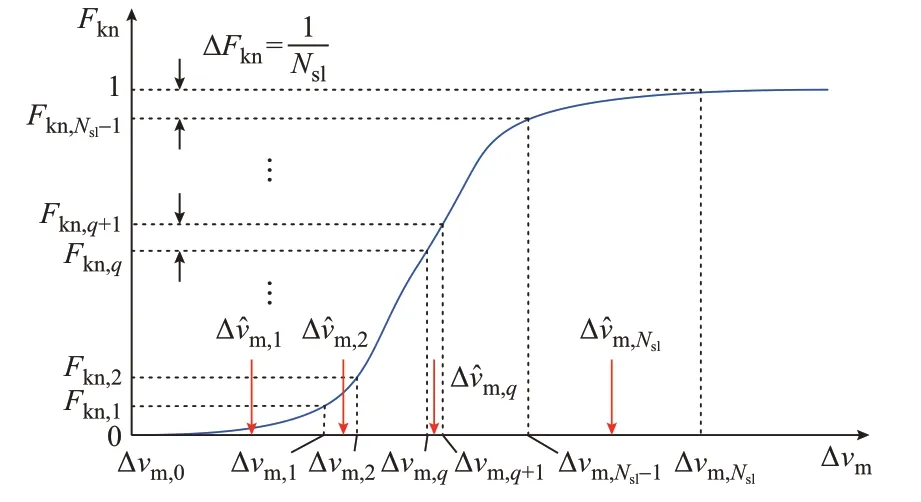
图3 拉丁超立方抽样原理Fig.3 Latin hypercube sampling principle

首先，确定所需抽取的样本总数为Nsl。然后，将累计概率分布曲线按照纵轴（累计概率）等间距划分为Nsl个区间，间距ΔFkn=1/Nsl，形成Nsl+1 个区间分界点0，Fkn，1，…，Fkn，Nsl-1，1；横轴也对应形成Nsl个区间，分界点为Δvm，0，Δvm，1，…，Δvm，Nsl（Δvm，0表示上述Nsp个原始数据样本中数值最小的风速预测误差）。在横轴各区间内随机选取一个点作为该区间内的抽样结果，Nsl个区间分别对应抽取的Nsl个样本，如下：

3.3 风电场未来短期暂态有功支撑能力评估流程

以在t0时刻预估t0+τ时刻风电场暂态有功支撑能力为例，按照图3 所示抽样方法可根据t0+τ时刻的风速预测结果生成t0+τ时刻的Nsl种实际风速场景。要求在上述Nsl种实际风速对应的风电场正常运行场景下，给定同一个控制指令ΔP^add（待决策）且风电场自身安全约束均被满足的条件下，所有场景的风电场在0 至th时段内平均功率之和最大。基于场景法，将式（3）和式（4）模型进行拓展，即

式中：下标q表示第q（q=1，2，…，Nsl）个风速场景下对应的变量。

实际上，为排除抽样结果中部分极端情况的影响，一般通过设定置信度γ，要求Nsl组如式（23）所示的约束中至少有Nslγ组约束被满足。因此，可引入中间0-1 变量zcon，q表示第q个场景的所有安全约束是否被满足（zcon，q=1 表示满足）。关于约束是否满足的逻辑判断过程仍可采用大M法进行转换，此处不再赘述。最终，以≥Nslγ为约束表示置信度条件，即在最优控制指令下至少有Nslγ个场景满足安全约束。

综上所述，基于场景法对优化模型拓展，并不改变其MILP 问题的性质，仍可借助Cplex 求解器快速求解。最终，求解可得最优控制指令ΔP^add，并取该控制指令在各个风速场景下发后的0 至th时段平均功率的最小值（保证结果鲁棒性），作为t0+τ时刻风电场的暂态有功支撑能力预估结果，其整体流程见图4。

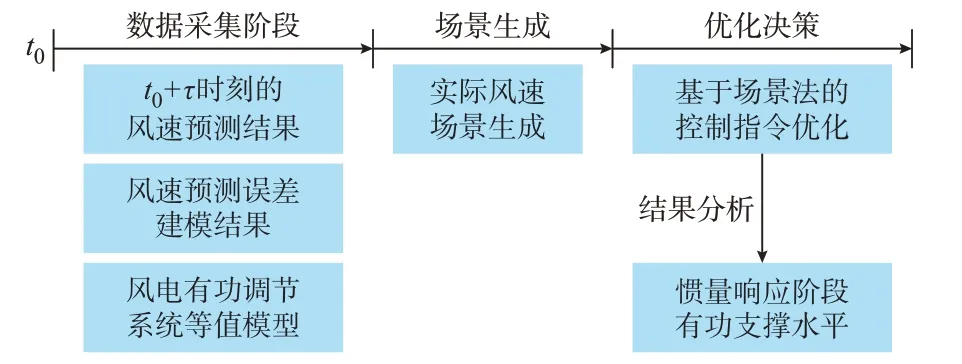
图4 风电未来短期暂态有功功率支撑能力评估流程Fig.4 Evaluation process of future short-term transient active power support capability of wind power

4 算例分析

4.1 仿真系统介绍

某地区实际风电场总装机容量为51 MW，包括30 台机型相同的双馈风机。单台风机结构参数与运行参数为：额定功率1.7 MW；额定风速12 m/s；风轮半径35.45 m；桨距角为0°时，对应的最优叶尖速比λopt为8，对应的最大风能利用系数为0.410 9；桨叶角速度基准值为2.48 rad/s，对应同步转速；桨叶角速度安全范围为0.7～1.2 p.u.；允许的最大电磁转矩为1.25 p.u.；网侧逆变器容量限制为0.3 p.u.，网侧初始无功功率为0.05 p.u.，值得说明的是，风电场功率的标幺基准为其额定功率；空气密度ρ为1.225 kg/m3；风机轴系多质量块惯性常数Hw为3.5 s（以额定功率为基准）。基于风电场历史风速预测与实测数据，得到预测风速落在[10.8，11.2) m/s 区间内时，预测误差统计与建模结果如图5 所示。

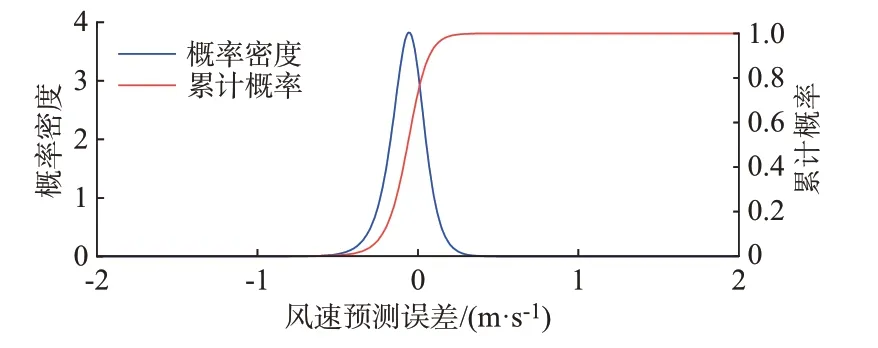
图5 实际风速的概率密度与累计概率Fig.5 Probability density and cumulative probability of actual wind speed

后续仿真基于MATLAB 2016b 及Simulink软件完成，所使用的计算机系统及硬件参数为：Windows 10，Intel i7-8700 3.2 GHz（CPU），16 384 MB 内存。

4.2 确定风速下的暂态有功支撑能力计算

本节主要针对不同风速（7～12 m/s）场景，计算采用图1 控制策略，在惯量响应阶段（此处设为0～3 s）风电场的暂态有功支撑能力。其中，不同风速场景下风机的初始运行参数见附录A 表A1。可见，风速由7 m/s 提升至12 m/s，风机的初始功率由0.198 5 p.u.提升至1 p.u.；风机的桨叶角速度由0.7 p.u.提升至1.2 p.u.。对应地，在模型分段线性化处理环节，风能利用系数-叶尖速比的非线性函数的分段线性化结果见附录A 图A1，可见分段线性化的精度基本满足后续计算要求。下述具体以风速为8 m/s 以及11 m/s 两个场景下的求解结果为例进行展示。

1）风速为8 m/s 的运行场景

优化所得最优调控指令为0.485 8 p.u.，对应0～3 s 内平均有功调节量为0.287 4 p.u.，该指令下风电场输出有功功率、桨叶角速度、转子侧输出功率以及转矩响应动态如图6 所示。

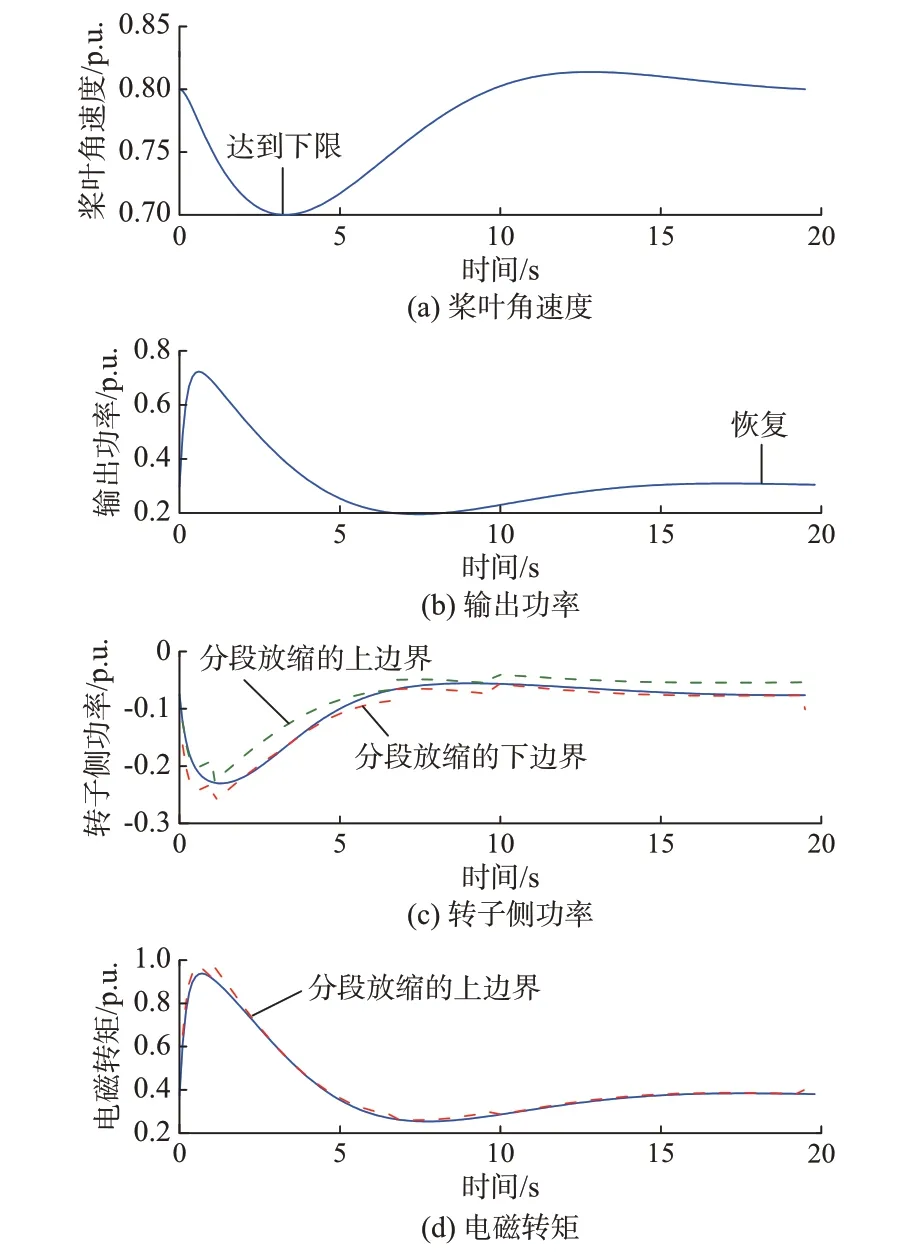
图6 风速为8 m/s 时最优上调指令下的风机响应动态Fig.6 Dynamic response of wind turbine with optimal up-regulation instruction when wind speed is 8 m/s

风速为8 m/s 的场景下，风机正常运行时桨叶角速度（0.8 p.u.）较低，而暂态功率上调将引起桨叶角速度下降，导致其暂态有功支撑能力主要受桨叶角速度安全下限0.7 p.u.的约束，如图6（a）所示。图6（c）与（d）的结果显示，式（15）与式（16）采用分段线性放缩的方式对转矩以及转子侧输出功率的计算结果基本与实际值相近，说明了该方法的准确性。

2）风速为11 m/s 的运行场景

优化所得最优调控指令为0.561 3 p.u.，对应0～3 s 内平均有功调节量为0.248 7 p.u.，该指令下风电场输出有功功率、桨叶角速度、转子侧输出功率以及转矩响应动态见图7。

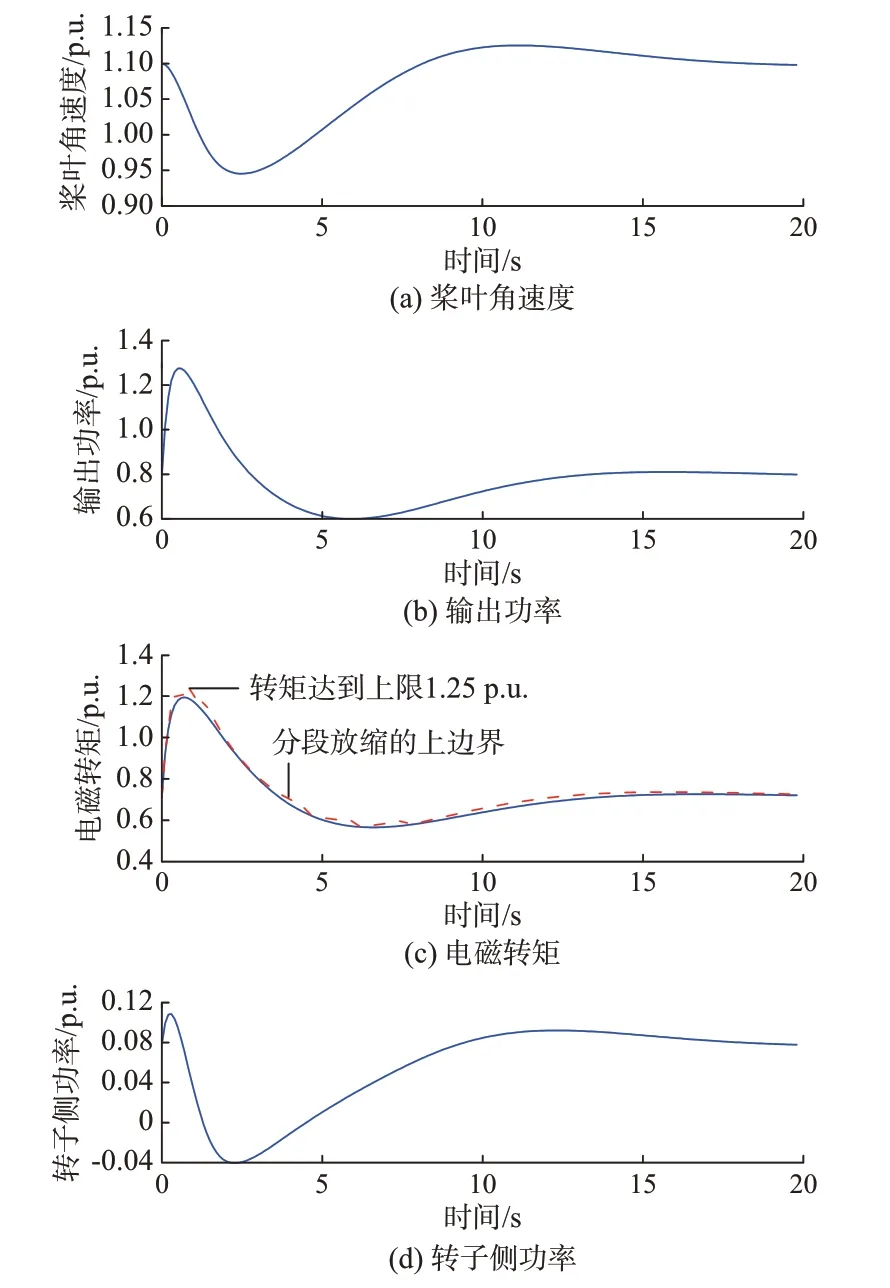
图7 风速为11 m/s 时最优上调指令下的风机响应动态Fig.7 Dynamic response of wind turbine with optimal up-regulation instruction when wind speed is 11 m/s

在风速为11 m/s 的场景下，风机正常运行时输出功率及电磁转矩较高，在暂态有功上调过程中电磁功率升高（图7（b）），而桨叶角速度反而下降（图7（a）），导致电磁转矩升高。因此，在该类高风速场景下其暂态有功支撑能力主要受最大电磁转矩1.25 p.u.的限制，具体表现为图7（c）中转矩线性化计算结果（与实际值相近）达到上限。

同理，以相同方式计算7～12 m/s 风速区间内其他风速场景下风电场暂态有功支撑能力，结果见图8。不同风速场景下风电场的暂态有功支撑能力以及调节受限主导因素存在一定差异，具体如下：

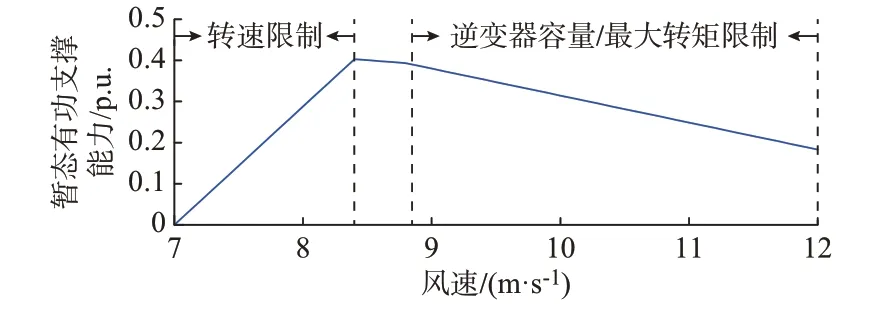
图8 不同风速下风电场的暂态有功支撑能力Fig.8 Transient active power support capability of wind farm with different wind speeds

1）在[7.0，8.4)m/s 的风速区间（初始桨叶角速度较低）内，其暂态有功支撑能力主要受桨叶角速度下限的约束，且风速越低对应的初始桨叶角速度越小，其有功上调裕度越低；

2）在[8.4，12]m/s 的风速区间内，风电场初始输出功率较大，其暂态有功支撑能力主要受转子侧逆变器容量/最大转矩限制，风速越高其有功上调裕度越小；

3）与［8.4，8.8］m/s 的风速场景相比，风速为［8.8，12］m/s 的场景下，风电有功支撑能力关于风速的变化速率稍大，这是因为在风速8.8 m/s 及以上的场景下进行暂态有功上调时，风机输出功率较大，触发了桨距角控制，使得风机暂态有功上调裕度下降。

值得说明的是，风电场设备配置以及运行要求的变化也将导致上述评估结果在数值上存在差异。经多次优化模型的求解验证，单个场站对应模型的求解耗时基本保持在12 s 以内，基本能够满足风电场暂态有功支撑能力评估的在线应用需求。

4.3 考虑风速预测误差的暂态有功支撑能力计算

本节以预测风速为11 m/s 的场景为例，结合图5 的风速预测误差建模结果，对风电场未来短期内暂态有功支撑能力进行评估。

首先，根据风电场风速预测误差的累计分布函数（见图5），抽取100 个随机样本，其对应的实际风速主要分布在[10.87，11.35)m/s 区间内，见图9。

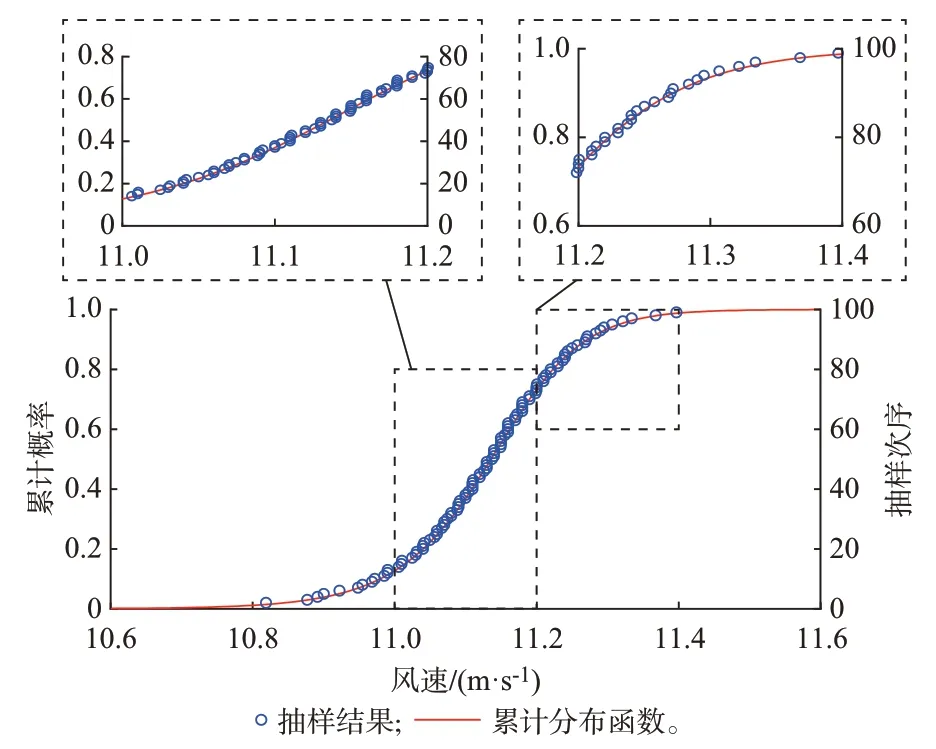
图9 拉丁超立方抽样结果Fig.9 Results of Latin hypercube sampling

由风速区间[11.0，11.2)m/s 与[11.2，11.4)m/s的抽样结果可见，累计分布函数曲线上斜率较大（对应概率密度较大）的风速区间内抽取的样本数较多。为了验证抽样结果的准确性，此处再次采用核密度估计对抽取样本的概率分布进行计算，并与图5 的概率密度函数进行对比，结果见图10。可见，核密度估计结果基本与原始数据概率密度曲线一致，说明了抽样的合理性。

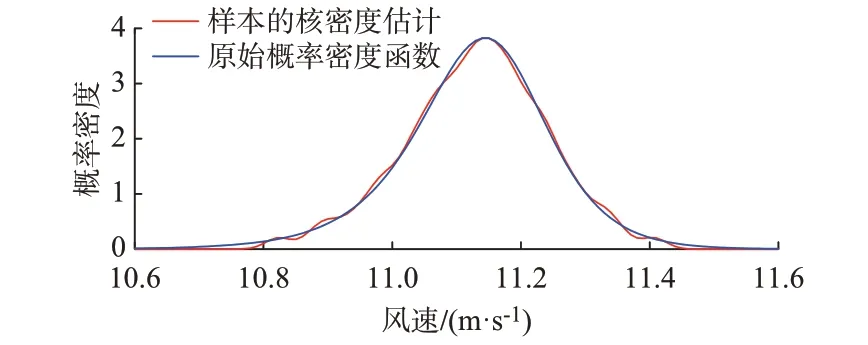
图10 样本的核密度估计结果Fig.10 Estimation results of kernel density of samples

事实上，可结合图8 所示风电暂态有功支撑能力-风速特性关系，对抽样场景进行筛选，然后代入3.3 节基于场景法拓展的优化模型进行求解，设置优化结果置信度为95%。根据图7 结果，在实际风速为11 m/s 的场景下，风电场暂态有功支撑能力为0.248 7 p.u；而优化所得面向多场景的最优有功调控指令为0.521 7 p.u.，暂态有功支撑能力为0.222 5 p.u.，略低于0.248 7 p.u。这是因为优化所得控制指令必须保证各个可能场景下风机均能安全运行，即要求评估结果具有一定鲁棒性。上述结果也表明，在部分风速区间内，风速预测误差对风电场暂态有功支撑能力的评估具有明显影响。

5 结语

本文提出了一种考虑风速不确定性的风电场暂态有功支撑能力评估方法，具体结论如下：

1）本文所构建的风电场暂态有功支撑能力在线评估模型可实现高效计算，基本能够在12 s 内实现单场站问题的求解，能够满足在线应用的需求；

2）在不同风速场景下限制风电场暂态有功调节的主导因素存在差异，在较高的风速环境下主要受逆变器容量/最大转矩限制，而在偏低的风速环境下主要受转速安全下限的约束；

3）在不同风速区间内，风速不确定性对风电场暂态有功支撑能力评估结果造成的影响存在差异性。一方面体现在不同风速等级下风速预测误差分布不同；另一方面体现在实际风速变化引起风电场可调裕度的变化程度也因风电场运行状态（与风速有关）存在差异。

本文主要分析了快速释放风机转子动能方式下风电场的暂态有功上调能力。在今后的研究中，将进一步综合考虑风机多类型有功下调措施，构建风电场暂态有功下调能力评估模型。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。