基于TQI-T的高速铁路道岔区轨道几何不平顺状态评价方法

秦航远，杨飞，孙宪夫，刘维桢

(1.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081；2.北京交通大学 机械与电子控制工程学院，北京 100044)

作为轨道结构中的薄弱环节，高速道岔是高速铁路轨道状态管理中的重要一环。其中，高速道岔的轨道几何不平顺状态直接影响其服役性能，较大的道岔区段轨道几何不平顺可能导致列车过岔时通过性能下降，出现晃车、抖车等现象，影响旅客的乘坐舒适性。当前，我国高速铁路动态轨道几何不平顺评价标准主要有峰值管理标准与均值管理标准，其中均值管理标准即使用当前国内外常用的轨道质量指数(Track Quality Index，TQI)作为评价指标[1]。在TQI 算法研究方面，我国最早于1991 年开始使用TQI 作为轨道状态管理依据[2]。魏世斌等[3]详细介绍了轨道质量指数的研究和应用情况。周正等[1]在TQI 计算中提出将满足部分条件的检测波形作为噪声处理的方法，有效提高了TQI 计算精度。杨飞等[4]提出了滑动标准差TQI计算方法，有效提高了利用TQI识别超标区段的效果和一致性。LASISI等[5]提出了一种将轨道安全性与轨道质量相结合的混合轨道质量指数，并评估了基于时间的相关参数对轨道质量的影响。WANG 等[6]提出了基于激励因子的动态综合评估方法来评估高速铁路轨道的几何状态。在指导线路养护维修等应用方面，许玉德等[7]计算了既有线的TQI及各单项不平顺，并统计了其分布特性，科学评估了既有线路的轨道状态。王俊文[8]详细阐述了TQI 的应用现状，并提出建立基于TQI 的“天窗修”专家决策系统，用于指导我国铁路养护维修。朱芳草等[9]提出了基于灰色理论的轨道质量指数定量预测方法。赵玉林等[10]提出了基于改进非等时距灰色组合模型的轨道质量指数预测方法，该模型较传统灰色模型有着更高的准确性。赖思成等[11]基于灰色区间理论，对重载铁路轨道质量指数进行了预测。FALAMARZI 等[12]以有轨电车为研究对象，提出了针对有轨电车的TQI 评价指标。XIAO等[13]采用TQI等一系列指标比较了聚氨酯道床与无砟轨道区段的轨道几何状态。SADEGHI 等[14]采用神经网络手段建立了轨道几何缺陷与轨道结构问题之间的相关性关系。CHOI 等[15]采用基于荷载的轨道不平顺分析技术对有砟线路轨道几何与轮轨力动态检测数据和现场测量数据进行对比分析，证明了轨道不平顺与轮轨相互作用力之间的相关性。目前，TQI主要用于评价正线区段的轨道几何状态，在道岔区段动态轨道几何状态研究方面，王峰等[16]通过比较国内外新建客运专线道岔轨道几何静、动态验收标准，给出了我国新建客运专线道岔轨道几何尺寸验收标准建议值。刘芳[17]针对性提出了增加横向约束以控制桥上无缝道岔轨道稳定性的方法并在现场实地进行了验证。全顺喜等[18-19]系统性研究了道岔区几何不平顺控制方法和其对行车安全性与平稳性的影响。然而，TQI在道岔区段的应用效果仍不理想，主要存在以下2个方面问题：一是TQI计算时需将轨道按照等里程间隔划分单元，长度为200 m，这会导致道岔区附近的各轨道单元可能同时包含1 至2 组道岔的部分或全部区段，无法对某一组道岔进行针对性评价；二是针对存在动态轨距优化的CN 系列道岔，由于轨距加宽区段的轨距与轨向存在由结构设计特性所导致的检测数据大值，导致包含该道岔的轨道单元TQI计算结果过大，无法准确反应其真实轨道状态。综上，基于道岔精确定位技术，综合考虑CN系列道岔尖轨区段轨距加宽影响，提出基于道岔区轨道质量指数(Track Quality Index of Turnout，TQI-T)的高速道岔轨道几何不平顺评价方法，针对性评价道岔区段轨道几何不平顺状态，为道岔区轨道几何不平顺整治工作提供科学指导。

1 基于区段道岔定位指数与置信系数的道岔精确定位方法

在道岔尖轨与心轨尖端位置，由于钢轨刨切及组合廓形的影响，轨道几何检测系统在此处往往存在一定程度的检测数据小幅跳变现象。以此现象为特征，设计相关算法对其进行针对性精确提取，提出基于区段道岔定位指数与置信系数的道岔精确定位方法，详细算法如下所示：

1) 采用基于曲线信息的绝对里程修正算法，对实测轨道几何检测数据进行里程修正，详细修正算法可参照文献[20]。

2) 根据实测轨距与计算轨距求得实测与计算轨距偏差量Δg。

3) 对Δg进行滤波，滤除其趋势项，保留高频成分Δgh。

4) 按照公式(1)计算Δgh的移动有效值Sg。

其中：N为采样点总数，K为窗长。

5) 将Sg除以其平均值，得到道岔定位指数Ig及其归一化指数Ig0：

其中：Igmax为分析区段内道岔定位指数最大值。

6) 根据道岔台账尖轨尖里程信息，将相隔一定里程范围内道岔划分为同一区段，分别提取各区段轨道几何检测数据。

7) 根据某一区段内各组道岔的台账尖轨尖端里程信息lk(k=1,…,M，M为该区段内道岔总组数，k按照各组道岔尖轨尖端里程从小到大依次递增)，提取其前后一定范围内[lk-d,lk+d]的道岔定位指数Ig(i)及里程数据m(i)，其中{i|m(i)∈[lk-d,lk+d]}，d为提取区段长度之半，提取其中道岔定位指数最大值点Ig()，Ig0()及对应里程，其中为道岔定位指数最大值点对应采样点编号。

8) 根据公式(4)计算Ig()对应置信系数：

则c0取1/2，否则c0取1；参数a和b则根据预设数值反解方程得到，文中暂定：

通过上述方程解得a和b数值。

其中相关参数参照步骤8中定义。

其中相关参数参照步骤8中定义。

2 道岔区轨道质量指数计算方法

在道岔区段轨道几何数据精确识别及提取的基础上，综合考虑CN 系列尖轨区段动态轨距优化的影响，对各型号高速道岔及其前后一定里程范围内轨道几何不平顺状态进行综合性评价，提出基于TQI-T 的道岔区轨道几何不平顺状态评价方法，详细算法如下所示。

1) 若某区段第k组道岔尖轨尖端里程为，心轨尖端里程为，计算该组道岔岔前与岔后接头里程和：

其中，d1为道岔尖轨尖端与岔前接头间距，d2为道岔心轨尖端与岔后接头间距。

2) 设道岔延拓距离为lext，确定道岔轨道质量指数计算区段[mtqi1,mtqi2]或[mtqi2,mtqi1](根据mtqi2与mtqi1相对大小确定)：

3) 若该组道岔为CN 系列道岔，则根据该型号CN 系列道岔及其前后40根正线轨枕范围内区段的各轨枕间距信息，按照公式(11)生成各个轨枕处相对岔前接头的里程，其中r=-40,…,1,2,…,Nslp+40，Nslp为该型号道岔岔枕总数。

4) 提取待分析型号道岔心轨尖端对应里程mx0，以辙叉号为18 的CN 系列道岔为例，该型号道岔第93 与94 号岔枕中间位置对应心轨尖端，则该型号道岔心轨尖距岔前接头里程mx0为：

6) 对Al0(i)及Ar0(i)，i=k1,k1+1,…,k2进行带通滤波，滤波波长参考目前高速综合检测列车轨道几何检测系统的中波轨向波长范围，为防止边际效应，滤波前需对Al0(i)及Ar0(i)，i=k1,k1+1,…,k2前后进行补零延拓，记滤波后得到的理论轨向为Al(i)及Ar(i)，i=k1,k1+1,…,k2。

7) 根据文献[21]中方法对道岔开向进行判断，识别实测数据左右股与直曲基本轨的对应性，将道岔区段轨距及左右股轨向实测数据与理论值作差，消除轨距结构加宽所带来的影响，以左股对应直基本轨为例，计算方式如下(右股对应直基本轨时则将Al与Ar调换)：

其中，gtqi，altqi和artqi分别对应消除结构加宽影响后的轨距及左右股轨向；g，al和ar分别为实测轨距及左右股轨向。

8) 计算[mtqi1,mtqi2]或[mtqi2,mtqi1]区段内左右高低、左右轨向、水平、三角坑与轨距标准差之和，当所分析道岔为CN 系列道岔时，即为TQI-T，道岔区段内轨距及左右股轨向替换为gtqi，altqi和artqi。

其中，xpq为轨道几何不平顺检测数据，p代表单项不平顺通道序号，从1 至7 分别对应左右高低、左右轨向、水平、三角坑与轨距，q代表采样点序号，Nt代表计算区段总采样点数，其中轨距与左右轨向为经步骤7与8处理后数据，即gtqi，altqi和artqi。

3 算例分析

对某高铁线路轨道几何检测数据中CN 系列道岔进行识别，验证方法对道岔区段提取效果。为了更好地标明道岔区段，将轨距检测数据与定位指数进行同步展示，结果如图1所示，所用延拓距离为25 m。其中图1(a)表示基于道岔定位指数的道岔区段提取效果，图1(b)通过CN 道岔轨距检测波形验证图1(a)中的道岔尖心轨尖端位置，实线为原始检测数据，圆圈为所提取区段或动态轨距优化区段数据。可以看出，在尖轨尖端与心轨尖端位置，道岔定位指数存在明显大值。经现场勘查与分析，此处大值的产生是由于在轨道几何检测系统的激光传感器对尖轨与心轨组合廓形进行采集的过程中，随着尖轨与心轨轨顶的升高，轨顶下16 mm的轨距定位点位置从基本轨或翼轨突然跳变至尖轨或心轨所导致。而心轨相对翼轨降低值从大于16 mm 变化至小于16 mm 的过渡区间长度小于0.25 m(即轨道几何检测系统的采样间隔)，因此可认为此处大值点即对应道岔心轨尖端，而另一处大值点则位于尖轨尖端附近。可知上述2处大值点的产生是由于道岔组合廓形的设计特点所引起，在轨道几何检测过程中稳定出现，与道岔钢轨服役状态等因素无关。综上，基于所提出方法，可实现对待计算道岔区段以及CN 系列道岔轨距加宽区段的准确识别提取，为道岔区段轨道几何不平顺评价指标的计算提供准确可靠数据支撑。

图1 TQI-T计算区段与轨距加宽区段识别Fig.1 Identification of TQI-T calculation section and gauge widening section

CN 系列18 号道岔轨距及左右股轨向实测值、设计值(其中轨向通道设计值为经1.5～25 m波长滤波后设计值)与实测值相对设计值偏差量计算结果如图2所示。可以看出，各通道实测值与设计值一致性良好，说明采用心轨尖端位置对实测几何数据与理论设计数据进行里程对齐的精度较高，满足TQI-T指标计算要求。同时可以看出，由于动态轨距优化设计的影响，CN 系列道岔尖轨区段轨向及轨距数据存在明显大值，此外轨向数据由于滤波器的影响存在一定的波动，而经预处理后上述大值及波动均得到了消除，准确还原了CN 系列道岔轨距加宽区段的实际轨道几何偏差量，为TQI-T的计算提供了准确的数据基础。

图2 18号CN道岔轨距轨向实测值、设计值与实际偏差量计算结果Fig.2 Calculation results of measured value,design value and actual deviation of gauge and track direction of 18# CN turnout

选取多条250～350 km/h 速度级无砟高铁线路共计859 组正线道岔3 653 次轨道几何检测数据(平均每组道岔检测4.25 次)，对比分析不同计算方式所得到的道岔区轨道几何不平顺评价指标，研究不同计算方式下道岔区轨道几何不平顺评价指标分布特性及评价效果。各型号道岔分析情况如表1所示。

表1 各型号道岔分析组次数统计Table 1 Statistics of analysis times of various types of turnouts

分别提取上述859组道岔精确定位前后的尖轨尖端及其前后各100 个采样点(共计50 m 区段)的历次轨道高低检测数据，对同一组道岔的历次高低数据进行相关性分析，得到精确定位前后的轨道高低波形相关系数如图3所示。可以看出，精确定位前各组道岔的历次数据间相关系数主要分布在0.87～0.96 范围内，而精确定位后各组道岔历次检测数据之间的相关系数得到了显著提升，主要分布在0.95～0.99范围内。说明道岔精确定位算法在面对海量数据的分析过程中能够有效进一步提高历次检测数据的道岔定位精度，为TQI-T的准确计算奠定了良好的数据基础。

图3 精确定位前后同组道岔历次检测数据相关性分析对比Fig.3 Data correlation analysis and comparison of each inspection of the same turnouts before and after precise positioning

以辙叉号为18的CN系列道岔区段的轨道几何检测数据为分析对象，对比不同计算方式得到的轨道几何不平顺评价指标累计分布如图4所示，图中偏右侧曲线为无预处理下计算得到的轨道几何不平顺评价指标，中间曲线为对轨距轨向进行预处理后计算得到的对应指标(即TQI-T)，偏左侧曲线为客专系列18 号道岔轨道几何不平顺评价指标(同为TQI-T)。计算区段为岔前与岔后接头分别向前向后延拓25 m。

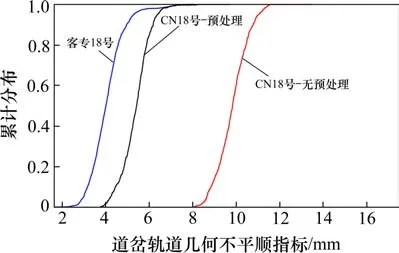
图4 CN系列道岔轨距轨向预处理效果Fig.4 Pretreatment effect of gauge and track alignment for CN series turnout

从图4可以看出，相比无预处理方式，采用预处理轨距轨向的方式对CN系列18号道岔的轨道几何不平顺状态进行计算，得到的几何不平顺评价指标显著减小，且与客专系列18 号道岔几何不平顺状态指标更为接近，说明TQI-T计算方法有效消除了CN 系列道岔由于动态轨距优化技术而产生的轨道几何不平顺对相应评价指标的影响。

采用如表2 所述5 种不同区段划分方式，对比不同计算方式下CN 系列道岔轨道几何不平顺评价效果如图5 所示，其中图5(a)为未对加宽区段轨距及轨向进行预处理计算结果，图5(b)为预处理后计算结果。需要指出，表2中区段1，2和3即为不同延拓长度下的TQI-T计算区段。

表2 不同区段划分方式Table 2 Different section division methods

图5 CN系列道岔不同计算方式结果对比Fig.5 Comparison of results of different calculation methods for CN series Turnouts

从图5可以看出，在未对轨距及轨向进行预处理时，18号CN 道岔不同延拓长度计算得到的道岔区轨道几何不平顺评价结果整体分布于8～10 mm附近，预处理后则整体分布于4～6 mm 附近。随道岔前后延拓长度增加，预处理前计算结果有较大幅度下降，预处理后不同计算区段所得计算结果整体分布则更为接近。此外，区段4划分方式可能导致计算区段内包含待计算道岔前后道岔部分区段，且针对大辙叉号道岔则无法覆盖其全长；区段5 所用200 m 计算区段可能包含多组道岔全部或部分区段，导致区段4 与5 计算结果离散性较大。

基于上述859组正线道岔多次轨道几何检测数据，计算表2中不同区段划分方式下同组道岔历次检测所得轨道几何不平顺评价结果方差，用于对比不同计算区段划分方式下的道岔区轨道几何不平顺评价指标计算结果一致性，结果如图6 所示，并取其均值，结果如表3所示。

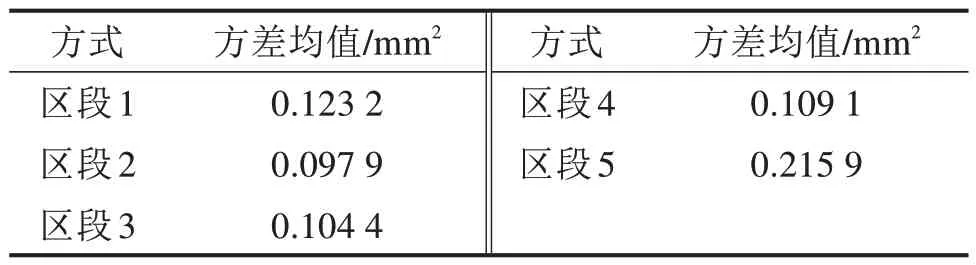
表3 不同区段划分方式计算一致性对比Table 3 Comparison of calculation consistency of different section division methods

图6 不同计算方式下同组道岔历次轨道几何不平顺评价指标方差统计对比Fig.6 Statistical comparison of variance of track geometric irregularity evaluation indexes of the same group of turnouts under different calculation methods

可以看出，相比于区段5(即当前200 m 区段TQI计算方式)，前4种区段划分方式下方差均值均下降约50%，体现出更好的计算一致性。说明基于道岔精确定位方法的区段划分方式有效提高了道岔定位精度，克服了历次检测里程相对误差对区段轨道几何状态评价指标带来的影响。同时，采用区段5可能导致计算区段内同时包含超过一组道岔的部分或全部区段，无法对某一组道岔进行针对性评价。此外，由于42 号等大辙叉号道岔全长超过100 m，导致采用区段4 则无法完全覆盖大辙叉号道岔全长，在适应性上有所欠缺；而根据《高速铁路设计规范》要求，正线高速道岔的最小间距不得小于25 m[22]，采用区段3则可能导致计算区段内会包括待评价道岔前后道岔的部分区段。综上并结合方差均值计算结果，以区段2方式划分道岔计算区段效果最为理想。

以区段2 方式划分计算区段，对客专与CN 系列18 号、42 号高速道岔TQI-T 的70%，80%及90%分位数进行统计，结果如表4所示。根据国内外区段均值管理经验，一般按照80%分位数作为各型号道岔的轨道几何不平顺评价阈值，客专18号、42 号、CN18 号、42 号道岔TQI-T 的80%分位数分别为4.6，4.3，6.0与5.1 mm，因此建议250～350 km/h速度级高速道岔TQI-T管理值仍沿用《高速铁路线路无砟轨道维修规则》中的5.0 mm 作为试用管理值，以待后续大量理论及试验的验证并最终确定相关评价标准。

表4 区段2方式下TQI-T分位数统计Table 4 Statistics of TQI-T quantiles in sector 2 mode

4 结论

1) 基于区段道岔定位指数与置信系数的道岔精确定位技术能够综合考虑岔区前后多组道岔相互位置关系，快速确定各组道岔尖心轨尖端里程，有效提高了现有道岔定位技术的定位精度。

2) 相比现有TQI评价方式，TQI-T 能够更为精确地对道岔及其前后一定范围内轨道几何不平顺进行针对性评价，具有更好的准确性和一致性。

3) 道岔区前后延拓距离为25 m 时计算结果一致性最佳，建议将其作为TQI-T 指标延拓距离参数，并以80%统计分位数作为各型号高速道岔的管理阈值，管理阈值取5 mm 较为合适，可作为试用管理值。