基于联合概率法的重载铁路大跨钢桁梁桥剩余疲劳寿命评估

郭文华，蒋晨奕

(中南大学 土木工程学院，湖南 长沙 410075)

随着我国经济水平不断提高，我国铁路货物运输急需通过扩大列车编组长度、加大列车轴重、增加行车密度等方式发展。开行重载列车，将使铁路大跨度钢桥构件及局部细节的疲劳荷载效应加剧，可能出现结构局部损伤、提前老化等疲劳问题，直接影响桥梁的正常使用和安全运营。钢桁梁桥由于跨越能力大、自重轻、施工周期短等优点得到了广泛应用，目前常采用正交异性整体桥面，由于焊缝数量多，焊接质量参差不齐，可能造成疲劳损伤。因此，开展重载铁路钢桁梁桥及其正交异性整体桥面的疲劳分析与剩余疲劳寿命评估对确保桥梁运营安全及科学开展维修养护均有重要指导意义。国内外学者主要采用理论分析、数值仿真、模型试验、现场实测等方法对钢桁梁桥疲劳性能进行了深入的研究。朱志辉等[1]基于车桥耦合理论对重载铁路64 m 简支钢桁梁桥中采用明桥面的纵梁进行局部疲劳分析；时岩[2]采用有限元分析与试验相结合的方法，探究30 t轴重列车对64 m 简支钢桁梁桥和连续钢桁梁桥运营能力的影响；肖鑫等[3]根据实测车辆荷载数据，对钢桁梁桥下弦杆和斜杆开展疲劳可靠性分析；李旺旺等[4]建立车-桥耦合模型，分析重载列车作用下48 m 钢桁梁桥的动力性能；王振宇[5]采用有限元分析与现场试验相结合的方法，探究重载铁路64 m简支钢桁梁桥的疲劳性能及加固技术；李慧乐等[6]基于车桥耦合随机振动分析对钢桁梁桥纵梁端部横梁处高强螺栓连接开展疲劳可靠性评估；卫星等[7]探究铁路32 m正交异性板桥面上承钢桁梁的疲劳开裂原因；GUO等[8]基于交通荷载模型对正交异性钢桥面板的多个疲劳部位进行疲劳可靠性评估；ADASOORIYA[9]提出一种概率疲劳评估方法，预测六跨连续钢桁梁桥剩余疲劳寿命；BERTOLESI等[10]将数值模拟、实验室疲劳试验和现场试验相结合，综合分析某六跨连续钢桁梁桥的剩余疲劳寿命。综上所述，针对重载列车作用下采用正交异性钢桥面板的大跨简支钢桁梁桥的疲劳分析还较少，且大多未考虑线路年运量、大轴重长编组列车的未来发展趋势以及车辆载重、车速的随机性，无法真实反映铁路钢桁梁桥的剩余疲劳寿命。为准确获得重载铁路大跨简支钢桁梁桥的累积损伤度和剩余疲劳寿命，以某108 m 简支钢桁梁桥为研究对象，基于Midas/Civil 软件建立包含正交异性整体桥面的钢桁梁桥有限元模型，采用考虑车桥耦合振动影响的重载列车移动简谐荷载来计算列车通过桥梁时的动力响应，依据动力响应结果确定疲劳控制杆件和相应的疲劳部位，分析各疲劳控制部位的疲劳应力谱，探究运营列车类型、车速、车辆载重、编组车辆节数等对钢桁梁桥疲劳损伤的影响，根据等效列车历史运营谱和可考虑年运量及典型疲劳列车发展趋势的未来运营谱，并考虑车辆载重及车速的随机性，采用联合概率法开展桥梁的疲劳性能评定和剩余疲劳寿命评估。

1 基于联合概率的铁路钢桥疲劳分析方法

1.1 列车移动模拟荷载

为计算列车运行产生的桥梁动力响应，有些学者直接采用移动集中力法来模拟列车荷载[11-12]。显然移动集中力法没有考虑列车本身振动及轨道不平顺的影响，仅近似反映了列车过桥时的动力效应[13]。为避免开展复杂车桥耦合振动计算，又能选用较真实的列车移动荷载，假定列车竖向振动荷载由作用在两侧钢轨上的移动荷载列组成，荷载排列与列车轮对排列相同，其大小采用静荷载与一系列正弦函数叠加的激振力来模拟[14]，作用在单根钢轨上的列车竖向振动荷载为：

式中：F0为单边静轮重；Fi为对应某频率振动荷载幅值；ωi为振动圆频率；m0为列车簧下质量；li和ai为轨道几何高低不平顺的波长与矢高。列车编组均假定由相同类型重载车辆组成。该列车移动荷载是根据大量试验数据总结出的半经验公式，具有一定的准确性和通用性，可反映一定的轨道状态与列车振动的影响[15]。

我国重载货物列车按轴重、轴距参数主要分为4 类：HV-21，HV-23，HV-25 和HV-30，如图1所示。F0取为轴重，列车簧下质量m0=650 kg，轨道几何不平顺波长l1=10.0 m，l2=2.0 m，l3=0.5 m；轨道高低不平顺矢高a1=6.00 mm，a2=0.80 mm，a3=0.12 mm。以重载列车HV-30 为例，当行车速度为110，120 和130 km/h 时，其单个竖向振动荷载时程曲线图如图2 所示。行车速度直接影响到3 个正弦函数的贡献比例，进一步使荷载时程曲线的稠密程度与幅值产生变化。

图1 重载车辆轴重、轴距参数Fig.1 Loads and wheelbase parameters of heavy-haul trains

图2 HV-30列车振动荷载时程图Fig.2 HV-30 vibration load time-history curve

1.2 疲劳应力谱求解

根据上述钢桁梁桥空间模型和典型疲劳列车移动模拟荷载，可分别计算不同类型列车在不同列车载重下以不同车速通过钢桁梁桥时的桥梁动力响应。然后通过编制MATLAB雨流计数法程序，针对计算得到的桥梁控制部位应力时程曲线，提取、统计出所有的应力幅值并制成疲劳应力谱(或疲劳应力统计直方图)。

1.3 疲劳损伤度

S-N曲线是表示构造细节疲劳寿命与外加常幅应力之间关系的曲线，是进行钢桥疲劳分析和疲劳设计的重要依据之一。钢结构S-N曲线表达式为[16]

式中：N为疲劳寿命；Δσ为疲劳应力幅；C和m为由构件和连接类别决定的相关参数；Δσ0为常幅疲劳应力临界值，一般取N=107对应的应力幅作为Δσ0。

根据Palmgren-Miner 线性疲劳累积损伤理论(简称Miner 准则或Miner 法则)，任意构件在变幅应力循环(Δσi，i=1，2，3，…)作用下的总损伤度D的表达式为

式中：ni为应力幅Δσi的循环次数，Ni为常幅疲劳强度曲线S-N曲线中相应于Δσi的疲劳寿命。

1.4 钢桥剩余疲劳寿命评估

开展铁路钢桥剩余疲劳寿命评估，必须首先调查分析等效列车运营谱，即每年通行的典型疲劳列车及相应的年通行频率，由此亦可估算出线路年运量的大小。分别根据线路上我国运营列车历史现状及预期规划情况，可统计分析得到等效列车历史运营谱及未来运营谱。其中，典型疲劳列车主要根据列车牵引总质量和列车类型决定，列车牵引总质量亦间接反映了编组车辆节数。目前主要考虑以下4 种典型疲劳列车：牵引质量0.5 万 t 的普通列车编组选用66 节HV-21 列车，表示为FT-0.5-21；牵引质量1 万t 的列车编组选用108 节HV-23 列车，表示为FT-1-23；牵引质量2 万 t 的列车 编组选用200 节HV-25 列车或167 节HV-30列车，表示为FT-2-25和FT-2-30。

现有研究[6,17]表明：对于典型疲劳列车，车辆载重和车速都服从正态分布N(μ，σ)。根据均值μ正态分布的“3σ”原则，把区间(μ-3σ，μ+3σ)作为置信区间，分别以μ为均值、σ为增量取7 级，计算各级出现的概率。基于联合概率法，假定典型疲劳列车每次通行时，应同时考虑车辆载重与车速的正态分布，需计算49 种工况。由于车辆载重与车速相互独立，每种工况出现的联合概率是载重概率与车速概率的乘积。依据正态分布概率密度函数的对称性，当列车通行频率一定时，每种典型疲劳列车完成的线路年运量不会因为考虑载重的正态分布而发生变化。因此，考虑车辆载重及车速的联合概率分布后，第j种典型疲劳列车通过一次钢桁梁桥时造成的平均疲劳损伤度dj为

式中：pv，j为第j种类型列车单独以第v级车速开行时的概率；pl，j为第j种类型列车单独以第l级车辆载重开行时的概率；dv，l，j为 第j种典型疲劳列车同时以第v级车速和第l级车辆载重开行时，通过一次钢桥时造成的疲劳损伤度，可通过分析该类列车以特定车速和车辆载重工况下通过一次桥梁时动力向应求得。则铁路钢桥运营到第y年的累积损伤度D(y)为

式中：Di为第i年的年损伤度；y为钢桥已经运营年数；Ti为第i年典型疲劳列车种类数，目前主要考 虑FT-0.5-21，FT-1-23，FT-2-25 和FT-2-30 等4种；fi，j为第i年内第j种典型疲劳列车的年通行频率，可直接反映线路总年运量的变化。开展剩余疲劳寿命评估时，当钢桥在第k年的累积损伤度D(k)值首次出现不小于1.0 时，则表明钢桥在第k年发生了疲劳破坏，钢桥剩余疲劳寿命为k-y年。

2 简支钢桁梁桥概况

简支钢桁梁桥因具有跨度大、自重轻、施工周期短等优点，在大秦铁路、朔黄铁路等货运铁路中得到广泛应用。以某I 级铁路货运专线的108 m 下承式简支钢桁梁桥为例，桥梁主桁采用三角桁式，主桁中心距13.6 m，桁高12 m，节间距12 m，弦杆采用箱形截面，腹杆采用箱形或H 形截面。本桥采用由桥面板、横梁、横肋、纵肋、边纵梁组成的正交异性板整体桥面系，两道横梁之间设3 道横肋，钢桥面共设置10 道横梁、27 道横肋、16道纵肋和4道边纵梁，如图3所示。

图3 正交异性桥面布置图Fig.3 Orthotropic bridge deck layout

采用Midas/Civil对108 m 简支钢桁梁桥进行建模，其中主桁架及联结系杆件采用梁单元模拟，正交异性整体桥面采用梁格法模拟。桥面二期恒载按附加质量单元模拟。为接近实际情况，定义质量为0，刚度较小的梁单元作为虚拟车道，通过在虚拟车道上添加移动车辆，模拟列车活载的作用。每片主桁架各设一个固定支座和一个活动支座。桥梁空间有限元模型如图4 所示，模型共有4 342个单元，2 650个节点。

图4 108 m简支钢桁梁桥有限元模型Fig.4 Finite element model of 108 m simple support steel truss girder bridge

3 疲劳控制部位确定

根据108 m 简支钢桁梁桥受力特点，对于主桁架，上弦杆在列车过桥中始终受压，故不必对其进行疲劳分析，仅选取下弦杆箱型截面棱角焊缝、腹杆箱型截面棱角焊缝或腹杆工字形截面翼缘板及腹板连续角焊缝作为疲劳计算控制部位。对于整体桥面，选取横肋跨中下翼缘纵向角焊缝、纵肋与桥面板焊接连接部位处作为疲劳计算控制部位。根据文献[16]，下弦杆、腹杆及横肋疲劳部位S-N曲线取值为m=3.5，C=13.45，则计算Δσ0h=69.6 MPa；纵肋疲劳部位S-N曲线取值为m=3.5，C=12.80，则计算Δσ0z=45.4 MPa。

以牵引总质量2 万 t 的HV-30 列车单次通过108 m 钢桁梁桥为例，车速为120 km/h，编组车辆节数为167节，计算得到了钢桁梁桥各疲劳控制部位的应力时程曲线，如图5 所示。列车在0.4 s 上桥，在70 s左右驶离钢桥。可以看出，下弦杆和腹杆的最大疲劳应力幅值分别为28.61 MPa 和28.67 MPa，均低于常幅疲劳应力临界值Δσ0h=69.6 MPa，不会出现疲劳损伤；横肋、纵肋的最大疲劳应力幅值分别为86.23 MPa 和51.33 MPa，均高于常幅疲劳应力临界值，可能发生疲劳破坏。其中横肋的最大疲劳应力幅值出现在其跨中下翼缘与腹板连接焊缝处、纵肋的最大疲劳应力幅值出现在其端部或跨中腹板与桥面板连接焊缝处，可确定这两类杆件的焊缝处为疲劳控制部位。

图5 桥梁主要杆件疲劳部位动应力时程曲线Fig.5 Dynamic stress time-history curves of the main fatigue parts

4 疲劳损伤度影响参数分析

4.1 列车类型的影响

为研究列车类型对钢桥疲劳的影响，选定车速为120 km/h，编组车辆数为100 节，选取了HV-23，HV-25 和HV-30 等3 种主要重载货物列车，分别计算了3种货车单次过桥时的桥梁动力响应。然后采用雨流计数法，计算了列车单次过桥时产生的疲劳应力谱。图6 和图7 分别给出了这3 种货车单次过桥时横肋、纵肋疲劳应力幅分布直方图。可以看出：横肋最大应力幅分别为57.40，68.77和82.97 MPa，纵肋最大应力幅分别为41.83，45.26和50.98 MPa，最大应力幅均随着轴重增大而增大，最大应力幅对应的应力循环次数仅为1次，主要由于列车进桥出桥产生；横肋、纵肋0～20 MPa的应力幅循环次数均占总循环次数的80%以上，主要由列车一直在桥上运行时产生；横肋疲劳部位处的应力幅水平总体上高于纵肋疲劳部位处。由于HV-23和HV-25列车单次过桥时横肋、纵肋最大应力幅均未超出相应的常幅疲劳应力临界值Δσ0，则HV-23 和HV-25 列车单次过桥时横肋、纵肋损伤度均为0。HV-30 列车单次过桥时横肋、纵肋的损伤度分别为1.85×10-7和1.50×10-7。

图6 横肋疲劳应力幅分布直方图Fig.6 Fatigue stress amplitude distribution histograms of transverse ribs

图7 纵肋疲劳应力幅分布直方图Fig.7 Fatigue stress amplitude distribution histograms of longitudinal ribs

4.2 行车速度的影响

为研究行车速度对钢桥疲劳的影响，选定HV-30 列车，编组车辆数为167 节，选取行车速度110～130 km/h，速度增量为5 km/h，分别计算了牵引总质量2 万 t 的HV-30 列车以不同车速通过桥梁时的动力响应。同理可计算HV-30列车以不同车速单次过桥时引起的横肋、纵肋的疲劳损伤度，如图8所示。可以看出，横肋疲劳损伤度随车速变化较小，纵肋疲劳损伤度总体随车速提高呈增大趋势，当车速大于120 km/h 时，纵肋疲劳损伤度增长尤其显著。列车振动荷载表达式中各正弦函数的幅值和频率与行车速度密切相关，且在按一定规律排列的列车荷载作用下，钢桥构件可能会在某些车速出现共振现象，因此疲劳应力幅及疲劳损伤随车速的变化比较复杂。

图8 不同车速下列车单次过桥产生的钢桥疲劳损伤度Fig.8 Fatigue damage degrees of the train crossing the bridge once at different speeds

4.3 车辆载重的影响

对于相同类型列车，由于每次列车装载货物多少的不同，会引起列车轴重发生变化，进而亦会对钢桥疲劳产生影响。选定HV-30列车，其自重为24 t，当车辆载重分别为80，88，96，104 和112 t，则列车轴重分别为26，28，30，32 和34 t。假定行车速度为120 km/h，编组车辆数为167 节，分别计算了不同车辆载重下HV-30列车单次过桥时引起的横肋、纵肋疲劳损伤度，主要计算结果如图9所示。列车过桥时横肋疲劳损伤度一般比纵肋更大，主要是由于列车作用下横肋应力幅明显大于纵肋所致；横肋、纵肋的损伤度均随车辆载重增加而增大，主要是由于车辆载重越大，钢桥动力响应也随之增大，造成钢桁梁桥疲劳细节损伤的疲劳应力幅亦增大所致。当车辆载重由104 t 变为112 t 时，横肋、纵肋损伤度分别显著增大了1.86 倍和1.44 倍，表明当车辆载重超过某临界值后，将对钢桥疲劳产生重大影响。

图9 不同载重下列车单次过桥产生的钢桥疲劳损伤度Fig.9 Fatigue damage degrees of the train crossing the bridge once under different loads

4.4 编组车辆节数的影响

编组车辆节数直接影响一线列车运量的大小，主要跟列车的牵引制动能力和线路状况有关。当选用HV-30列车时，按轴重30 t考虑，编组车辆数选取牵引质量5 000 t，1 万 t，1.5 万 t 和2 万 t 列车编组对应的42，84，126 和167 节。为研究编组车辆节数对钢桥疲劳的影响，计算了HV-30列车分别采用不同车辆节数以120 km/h 单次过桥时引起的横肋、纵肋疲劳损伤度，如图10所示。可以看出，横肋、纵肋疲劳损伤度均随编组车辆节数增长而有增大趋势，对横肋的影响更明显一些。

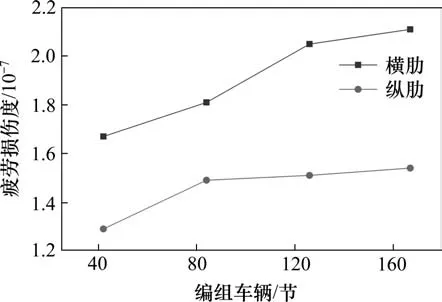
图10 不同车辆节数下列车单次过桥产生的钢桥疲劳损伤度Fig.10 Fatigue damage degrees of the train crossing the bridge once under different marshalling vehicles

5 剩余疲劳寿命评估

5.1 等效列车运营谱

等效列车运营谱主要包括等效列车历史运营谱和未来运营谱。SONG 等[18]统计分析了某重载铁路线路运营20 年来每年通行的典型疲劳列车及相应的年通行频率，限于篇幅主要统计资料列于表1。可以看出：为更大提高列车运量，我国典型疲劳列车有采用大轴重并且长联编组的发展趋势。本文采用相同的重载铁路历史运营谱，针对某重载铁路未来运营谱，结合年运量及典型疲劳列车发展趋势，预测未来运营从第21 年以后开行大轴重长编组列车FT-2-25和FT-2-30，年运量逐渐达到5亿t，并分为4个未来运营期，主要计算参数如表2所示。

表1 某重载铁路等效历史运营谱Table 1 Equivalent historical traffic spectrum of a heavy-haul railway

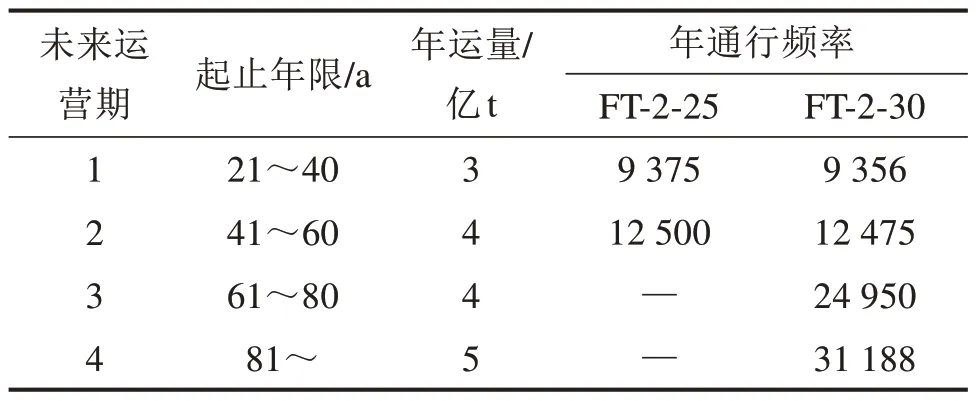
表2 某重载铁路未来运营谱Table 2 Future traffic spectrum of a heavy-haul railway

5.2 定值分析法与联合概率法计算结果对比

针对特定典型疲劳列车按年通行频率开展钢桥疲劳分析时，目前主要有2 种方法进行计算：1) 定值分析法：假定每次列车通行时，车辆载重和车速一直保持不变。以FT-2-30 为例，车辆载重一直为96 t，车速一直为120 km/h。2) 联合概率法：考虑车辆载重和车速的随机性，以FT-2-30 为例，假定车辆载重服从均值96 t、标准差8 t的正态分布，车速服从均值120 km/h，标准差5 km/h 的正态分布[6]。车辆载重分别取为72，80，88，96，104，112 和120 t 等7 级，依次出现的概率分别为0.6%，6.1%，24.2%，38.3%，24.2%，6.1% 和0.6%。同理，车速分别取为105，110，115，120，125，130和135 km/h等7级，依次出现的概率与车辆载重概率相同。每次列车过桥时，需同时考虑车辆载重与车速的正态分布，则需计算49种工况，每种工况出现的联合概率是载重概率与车速概率的乘积。例如：列车载重96 t和车速130 km/h出现的联合概率是2.34%。

根据上述定值分析法和联合概率法，分别计算了4种典型疲劳列车单次过桥时的钢桥横肋、纵肋损伤度，主要计算结果如表3所示。采用考虑列车载重、车速正态分布的联合概率法后，钢桥横肋、纵肋的疲劳损伤度均大于采用定值计算的损伤度结果，而且轴重较轻、编组较短的列车亦会对钢桁梁桥产生一定的疲劳损伤。由于考虑车辆载重及车速的随机性与真实列车运营情况更接近，故有必要考虑列车载重和车速的正态分布，才能使桥梁剩余疲劳寿命估算更准确合理。

表3 2种计算方法下列车单次过桥钢桥疲劳损伤度Table 3 Fatigue damage degrees of trains crossing the bridge once using two calculation methods

5.3 剩余疲劳寿命的计算

根据等效列车运营谱，同时考虑车辆载重和车速的正态分布，计算得到了钢桥横肋、纵肋累积损伤度随运营时间的变化曲线，如图11 所示。可以看出，在该线路已经运营的20 a，横肋、纵肋累积疲劳损伤度极小，主要是由于桥梁运营初期线路年运量较小，且运行的典型疲劳列车轴重相对较小且编组车辆节数较少。后期随着线路年运量的增长及大轴重长编组列车开行的增多，横肋、纵肋累积疲劳损伤度随运营时间增长明显加快。当桥梁运营到设计基准期第100年时，横肋、纵肋累积损伤度分别为0.41 和0.35，表明该108 m 简支钢桁梁桥抗疲劳性能良好。随着运营时间的增长，横肋、纵肋首次发生疲劳破坏时对应的运营时间分别为177 a 和214 a，考虑桥梁已运营20 a，故横肋、纵肋的剩余疲劳寿命分别为157 a和194 a。

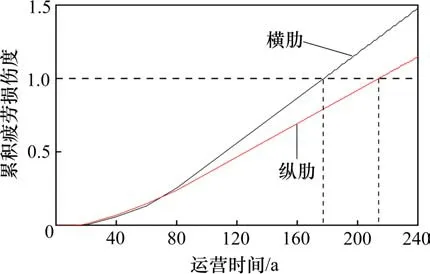
图11 累积疲劳损伤度曲线Fig.11 Cumulative fatigue damage degree curves

6 结论

1) 采用静荷载与一系列正弦函数叠加的激振力来模拟疲劳列车移动荷载，既可避免开展复杂车桥耦合振动计算，又能较好反映列车振动与轨道不平顺的影响，准确求解列车通过钢桥时的桥梁动力响应。

2) 108 m 简支钢桁梁桥主桁杆件的疲劳应力幅低于常幅疲劳应力临界值Δσ0，不产生疲劳损伤，最不利疲劳控制部位为正交异性桥面板的横肋跨中下翼缘纵向角焊缝以及纵肋与桥面板焊接连接部位。

3) 运营列车类型对横肋、纵肋疲劳应力幅和疲劳损伤的影响显著；疲劳部位损伤度随编组车辆节数的增大而增大，随行车速度的变化具有不确定性。横肋、纵肋的疲劳损伤度随车辆载重增加而增大，且当车辆载重超过某临界值后，将对钢桥疲劳产生重大影响。

4) 采用等效列车历史运营谱和未来运营谱可方便考虑线路年运量和疲劳列车长编组大轴重的发展趋势，进一步提出了考虑车辆载重、车速正态分布的联合概率法来开展钢桁梁桥疲劳分析，可更精确评估重载铁路整体桥面钢桁梁桥的剩余疲劳寿命。