基于EMD和SSA的股票预测模型
谢游宇,王万雄
甘肃农业大学理学院,兰州730070
股市是经济的晴雨表,各行各业的经营状况和发展前景都可以通过股市反映出来。如果能够预测和分析股市的走向,那么不仅能使投资者获益,也能够引导政府作出干预,避免股市崩盘。
股票序列具有非线性、非平稳等特征,同时含有大量噪声。传统统计模型如ARIMA[1]、GARCH[2]、VAR[3]、GM[4]等模型,虽然其具有完备的理论体系,可以根据统计原理来检验模型的优劣,但是传统统计模型对数据具有严格的假定如平稳性、正态性等,由于股票数据的非平稳性和非线性以及强烈的波动性,这也导致了传统统计模型在处理股票序列上具有局限性。相对于传统统计模型,机器学习模型和深度学习模型能够很好处理非线性非平稳序列,其对数据也没有任何假定,常用的机器学习模型和深度学习模型有支持向量机、随机森林、神经网络等。其中神经网络中的LSTM 模型对具有长期依赖性的数据有很好拟合效果,目前被广泛应用于股票预测[5-7];机器学习中的SVR 模型对于非线性序列具有很好的泛化效果,也常被用于股票预测[8-10]。
道氏理论认为股票指数存在三种趋势:长期趋势、中期趋势和短期趋势,并且股票变动受到这三种趋势的共同作用。因此有学者采用了分解的思想:将金融序列分解成具有不同时间尺度的若干分量,再分别利用单一模型对各个分量进行预测,最后再集成得到预测结果。基于这种思想,有学者提出了组合模型[11-13],这些组合模型大都采用了目前常用的数据分解方法:傅里叶变换、小波变换和经验模态分解(EMD);与小波变换和傅里叶变换不同,EMD 仅仅依靠数据自身的特征来进行信号分解,而不依赖基函数;基于这一特点,EMD 几乎适用于任何类型信号的分解,尤其是在非线性、非平稳序列上具有显著优势。因此有不少学者基于EMD得出了精度更高的股票组合预测模型如EMD-ARIMA[14]、EMD-SVR[15]、EMD-LSTM[[16]等模型。但是,经过EMD分解后得到的若干高频分量依然存在噪声,限制了模型的预测精度,有学者通过结合EMD 和SSA(奇异谱分析)两种方法成功实现了降噪[17]:对经过EMD分解后的所有分量再进行SSA 分解,从而实现信噪分离,使信号分解更彻底。在此,本文引入SSA对高频分量进行分解重构,实现对高频分量的信噪分离,进而提高预测精度。同时,SSA 本身也存在缺陷,其嵌入维度的大小将影响分解效果,较大的嵌入维度将使信号过度分解,较小的嵌入维度则无法有效提取特征;并且经过SSA分解后的第一个SSA分量往往混合了绝大部分特征,容易导致分解不全而无法充分提取特征,影响预测效果,故不直接对原始序列进行SSA 分解。因此,本文结合EMD和SSA 两种分解方法各自的优点,首先利用EMD 自适应性的优点将原始序列分解成具有不同特征的若干高频分量和低频分量以及残差项,其次利用SSA对所有高频分量进行重构,实现对高频分量的信噪分离。
鉴于此,本文提出了一种基于EMD和SSA的EMDSSA-LSTM-SVR的股票组合预测模型,并利用沪深300指数序列来验证模型的性能。首先利用EMD 将沪深300序列分解成具有若干不同时间尺度的IMF分量,再将各IMF分量进行组合:将低频IMF分量和残差项组合为趋势项,将剩余高频IMF 分量组合为波动项;其次利用LSTM 模型对趋势项进行预测,利用LSTM 模型和PSO-SVR 模型对波动项进行预测:首先利用SSA 对趋势项进行分解重构,利用LSTM 模型对长期依赖(自相关函数拖尾)子序列进行预测,利用PSO-SVR模型对短期依赖(自相关函数截尾)子序列进行预测,再将所有序列预测值合并为波动项预测值;最后将趋势项预测值和波动项预测值集成得到最终沪深300 预测值,如图1 所示。通过与LSTM、SVR、EMD-LSTM、EMD-SVR、SSALSTM和SSA-SVR六种模型对比,证明了本文所提组合模型的预测性能。

图1 方法与流程Fig.1 Methods and Processes
1 研究方法
1.1 EMD的基本理论
经验模态分解(empirical mode decomposition,EMD)[18],是一种信号分解的方法,其思想就是将信号分解为相互独立的多个本征模态函数(IMF)的叠加,IMF必须满足以下两个条件:
(1)函数在整个时间范围内,局部极值点和过零点数目必须相等,或者最多相差一个。
(2)在任何时间点,局部最大值的包络线(上包络线)和局部最小值的包络线(下包络线)平均必须为零。
算法流程如下:
步骤1 找到原始时间序列x(t)的所有极大值和极小值点,对所有极值点利用三次样条插值法拟合上包络线U(t)和下包络线L(t)。
步骤2 求上下包络线的均值M(t):
步骤3 原始序列减去均值包络线,得到中间序列h(t)。
步骤4 判断h(t)是否满足IMF的两个约束条件,如果满足则是一个IMF分量,如果不满足则返回步骤1反复迭代。
步骤5 假设h(t)是一个IMF 分量并记为IMF1,则重复步骤1~4,将M(t)当做原始序列继续分解得到下一个IMF分量IMF2,直到残余分量是单调函数或常量时,停止分解。残余分量记为res。
分解完成后,原始序列x(t)可以表示为:
1.2 LSTM的基本理论
LSTM(long short term memory,LSTM)[19]网络,是为了解决长期依赖问题而设计出来的一种神经网络模型,是一种循环神经网络(RNN)。所有的RNN 都具有一种重复的神经网络模块的链式形式,不同于标准RNN,LSTM 具有更为复杂的结构模块,主要通过三个门(输入门、遗忘门、输出门)来实现信息的记忆和传递以及状态的更新。
首先信息会经过遗忘门,遗忘门会读取前一时刻的输出以及当前时刻的输入,输出一个在0 到1 之间的数值ft,ft决定了信息的保留,1表示完全保留,0表示完全舍弃,如下:
其中,ht-1表示的是上一时刻的输出,xt表示的是当前时刻的输入,bf是偏置,σ是一个sigmod 函数。
其次信息会经过输入门,输入门决定了信息和状态的更新,主要包括两个步骤:一个sigmod 层决定哪些信息需要进行更新;一个tanh 层生成用来更新的内容,如下:
其中,Ct表示更新的信息,it为Ct的系数,Ct-1表示上一时刻的状态,C表示更新后的状态。
最后信息将会通过输出门,得到最终的输出值,输出值将会基于更新后的状态。首先,通过一个sigmod门确定哪一部分信息会被输出,接着把更新后信息经过tanh 处理并将它和sigmod 门的输出相乘,得到最终的输出,如下:
其中,ht为最终输出。
1.3 SSA的基本理论
奇异谱分析(singular spectrum analysis,SSA)[20],是一种处理非线性时间序列的方法,通过对所研究的时间序列的轨迹矩阵进行分解、重构等操作,提取出时间序列中的不同成分,从而实现对原始时间序列的分解和去噪。奇异谱分析主要包括四个步骤:嵌入—分解—分组—重构。
步骤1 嵌入。给一组有限长一维时间序列[x1,x2,…,xN],选择合适的窗口长度L(2 步骤2 分解。对矩阵S=XXT进行奇异值分解,得到如下形式: 其中,U为左矩阵;Σ仅在对角线元素有值,就是奇异值,其他元素均为零;VT为右矩阵。此外U、V均为单位正交矩阵。对S分解后会得到特征值λ1>λ2>…>λL≥0 和对应的特征向量U1,U2,…,UL。并且有: 步骤3 分组。将下标集合{1,2,…,d}划分成m个互不相交的子集I1,I2,…,Im,令I={i1,i2,…,ip},则对应于I的合成矩阵XI=Xi1+Xi2+…+Xip。则有: 其中,I1,I2,…,Im的选取过程即为分组。 步骤4 重构。将上式中的每个矩阵XIj变换为一个长度为N的新序列,即得到分解后的序列。令Y为一个L×K的矩阵,元素为yij,1 ≤i≤L,1 ≤j≤K。 令L*=min(L,K),K*=max(L,K),N=L+K-1,如果L SVR(support vector regression)[21]是一种基于结构风险最小化的回归算法,对于非线性数据具有很好的泛化能力,其核心思想是通过非线性映射将原始数据映射到高维空间,在高维空间寻找最优回归超平面,从而实现预测。 SVR的回归函数表达式如下: 其中,ω为权值系数,φ(x)为非线性变换函数,b为偏置。 不同于普通线性回归的损失函数,SVR的损失函数定义为: 其中,L[y,f(x)]为SVR的损失函数,ε为常数。只有当预测偏差小于ε时,才计算损失,否则不计入损失。上式相当于以f(x)为中心,构建了一个宽度为2ε的间隔带,只有落在间隔带以内的样本才不计算损失。 再通过引入松弛变量εi、ε∗i就可以得到SVR优化的目标函数: 其中,C为惩罚因子;为松弛因子。拉格朗日乘数法把式(17)的约束问题转化为无约束的二次规划问题求解,即原问题转化为如下对偶问题: 本文以沪深300指数来测试EMD-SSA-LSTM-SVR模型的预测性能,选取了2014 年1 月3 日至2021 年12月31 日共1 950 个收盘价数据,数据来源于Tushare 财经数据接口,如图2 所示。这段时间囊括了沪深300 指数上升、下降和震荡等多个阶段,同时沪深300 在一定程度上反映了整个股市的运行状况。因此,本文的测试数据具有一定代表性。 图2 沪深300Fig.2 hs300 2.2.1 EMD分解 沪深300 序列经过EMD 分解后一共得到8 个IMF分量,包含了4 个高频IMF 分量(IMF1~IMF4)和3 个低频IMF 分量(IMF5~IMF7)以及1 个残差项(IMF8)。这8 个分量分别对应了沪深300 存在的短期变动趋势(IMF1~IMF4)、中期变动趋势(IMF5~IMF7)和长期变动趋势(IMF8)。将4个低频分量合并为趋势项,再将4个高频分量合并为波动项,如图3和图4所示;经过EMD分解与重构后能够将原始序列分解为相对平滑的长期趋势项和具有高噪声的短期波动项。 图3 EMD分解Fig.3 EMD decomposition 图4 趋势项和波动项Fig.4 Trend and fluctuation terms 2.2.2 SSA分解 SSA存在嵌入维度选取问题,因此引入具有较强适应性的Cao[22]方法。利用Cao方法选取嵌入维度L的步骤如下: 计算不同嵌入维度L下最近邻点的距离变化值: 其中,‖ ⋅ ‖为无穷范数,Xi(L)与Xi(L+1)分别表示在嵌入维度为L和L+1 时重构的相空间向量,Xn(i,L)(L)则表示该向量的最近邻点。 计算相同嵌入维度L下相空间最近邻点变动值的均值: 观察E(L)的变化情况E1(L): 当E1(L)停止变动或者其值小于给定阈值时,此时的嵌入维度L0即为最佳嵌入维度。 利用Cao 方法对波动项进行SSA 分解,其E1(L)变化如图5所示,当L等于17时E1(L)趋于稳定,因此L=17为最佳嵌入维度。 图5 E1(L)变化Fig.5 E1(L)change 当嵌入维度为17 时,波动项经过SSA 分解得到的奇异值如图6所示,将奇异值大小相近的SSA分量合并[1,2,3-4,5-6,7-9,10-12,13-17],最终得到7 个SSA 分量,如图7所示。 图6 奇异值Fig.6 Singular values 图7 SSA分解Fig.7 SSA decomposition 经过SSA分解得到的7个SSA分量与经过EMD分解得到的4 个IMF(IMF1~IMF4)分量相比,SSA 分解能够将超高频分量(IMF1、IMF2)中的有效成分和噪声分离,从而减小噪声带来的影响。 经过EMD 和SSA 分解一共得到11 个不同时间尺度的子序列。道氏理论认为金融序列的中长期变动趋势在一定程度上有规律可循,因此将IMF5~IMF8 合并为一个长期趋势项来进行预测;而短期变动趋势较为复杂且不易把握,因此对剩余7个短期波动项分别单独预测。 本文选取均方根误差(root mean square error)、平均绝对误差和平均绝对百分比误差三种指标来检测模型的预测效果,计算公式如下: 其中,yi为序列真实值为序列预测值,n为序列长度,i为序列编号,三种指标的值越小,模型的预测精度就越高。 选取前6年共1 708个数据作为训练集,最后1年共242个数据为预测集来验证模型的预测性能,为了提高模型的求解速度和预测精度,在实证之前对模型进行归一化处理,归一化公式如下: 其中,x为原始序列,xmax为原序列最大值,xmin为原序列最小值。 利用LSTM模型对长期趋势项进行拟合,利用滑动窗口法预测下一期的值,根据趋势项的自相关函数将窗口值设置为180,采用单层LSTM网络,共50个神经元,激活函数为linear,损失函数为MSE,优化器为Adam,最大迭代次数为1 000 次,并设置了早停机制:当模型30次迭代后没有提升就停止迭代,并返回最优参数设置。 分别利用LSTM(参数设置同上)模型和PSO-SVR模型对重构后的7个SSA分量进行预测,同样采用滑动窗口法进行预测并根据其自相关函数来选取预测窗口长度,窗口长度分别设置为(30,20,15,10,7,5,4),最后将所有预测序列的结果合并得到沪深300 的预测结果。经过实证发现,LSTM 模型对前四个长期依赖(自相关函数拖尾)序列预测效果优于SVR模型,而对后三个短期依赖(自相关函数截尾)序列的预测效果劣于SVR 模型,因此利用LSTM 模型预测长期依赖序,利用SVR模型预测短期依赖序列。 为了凸显模型的优越性,本文还将LSTM、SVR、EMD-SVR、EMD-LSTM、SSA-LSTM 和SSA-SVR 六个模型与本文提出的EMD-SSA-LSTM-SVR 组合模型进行了对比,结果如图8~11所示。 图8 单一模型的预测值和真实值Fig.8 Predicted and true values for single model 图9 EMD分解模型的预测值和真实值Fig.9 Predicted and true values of EMD decomposition model 图10 SSA分解模型的预测值和真实值Fig.10 Predicted and true values of SSA decomposition model 图11 EMD-SSA-LSTM-SVR模型的预测值和真实值Fig.11 Predicted and true values of EMD-SSA-LSTM-SVR model 为了更加直观地比较各个模型的优劣,表1是各个模型的RMSE、MAE、MAPE三种指标,从劣到优分别是SVR、LSTM、EMD-SVR、EMD-LSTM、SSA-SVR、SSALSTM、EMD-SSA-LSTM-SVR。 表1 实验结果对比Table 1 Comparison of experimental results 结合图8~11 以及表1 可以看出,EMD-SVR、EMDLSTM、SSA-LSTM和SSA-LSTM模型要比单一模型SVR和LSTM 表现要好,经过EMD 分解和SSA 分解后的模型精度有明显的提升,而本文提出的EMD-SSA-LSTMSVR 模型的预测结果基本与原始沪深300 序列重合。由此可见本文提出的组合模型进一步提高了预测精度。 为了进一步验证模型的优越性和适应性,以本文提出的EMD-SSA-LSTM-SVR 模型为基础,对文献[15]和文献[16]中的数据进行预测,并与文献中的原模型的预测结果进行对比分析。 对于文献[15]中的上证指数收益率序列,以前976个数据作为训练集和测试集,后202 个数据为验证集,建立EMD-SSA-LSTM-SVR模型,预测结果如表2所示。 表2 上证指数收益率预测结果对比Table 2 Comparison of SSE index return forecast results EMD-SSA-LSTM-SVR 模型在三种指标上都要优于EMD-SVRF 模型,尤其在R-square,这也表明EMDSSA-LSTM-SVR模型具有更优秀的预测能力。 对于文献[16]中的综合指数指数序列,分别对沪深300、上证指数和深证成指建立EMD-SSA-LSTM-SVR模型,预测结果如表3。 表3 综合指数预测结果对比Table 3 Comparison of composite index forecast results 结合表2和表3的结果来看,EMD-SSA-LSTM-SVR模型无论是对相对平稳的收益率序列还是带有趋势的综合指数序列都有着良好的预测性能。 金融序列往往含有大量噪声,虽然EMD 分解能够自适应地根据序列自身特点将原始序列分解为多个时间尺度的子序列,但是其分解出的前几个高频子序列往往含有大量噪声,限制了其预测效果。SSA分解可以自适应地选择嵌入维度实现对序列的分解重构,将EMD分解后的高频分量再进行SSA 分解可以最大程度上实现对原始序列的完全分解,从而减小噪声带来的影响,最后再结合LSTM 模型处理长期依赖序列的优势以及SVR模型对非线性序列的泛化能力,建立了预测精度更高的EMD-SSA-LSTM-SVR模型。 本文提出了一种基于EMD 和SSA 的EMD-SSALSTM-SVR模型,该模型能够最大程度上实现对原始序列的完全分解,将原始序列分解为具有多个时间尺度的子序列,解决了EMD分解后高频分量存在的噪声问题,并且根据各个子序列的自相关函数选取相应的预测模型进一步提高了预测精度。同时以沪深300指数、上证指数、深证成指以及上证指数收益率进行验证,实验结果表明,EMD-SSA-LSTM-SVR模型具有更好的预测性能。1.4 SVR的基本理论
2 实证分析
2.1 数据来源
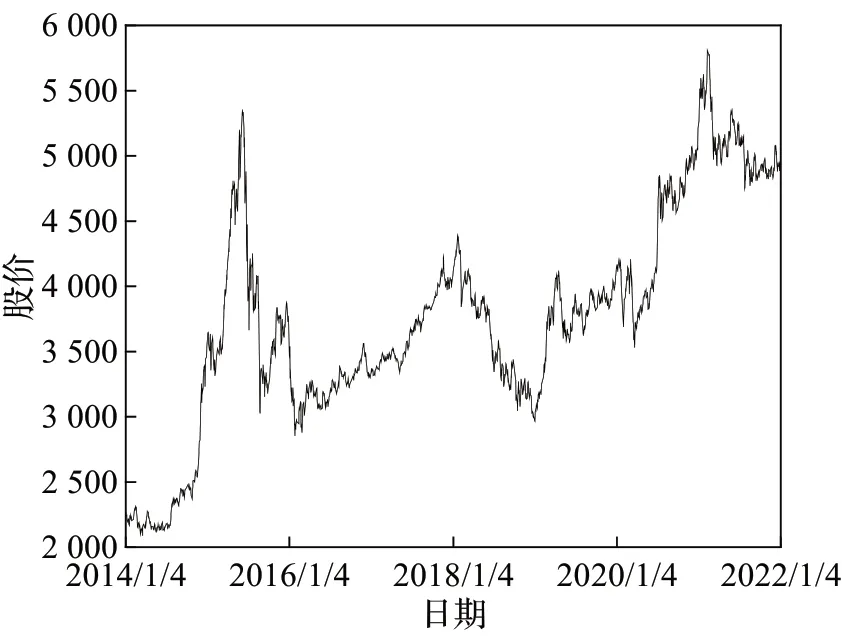
2.2 EMD分解与SSA分解
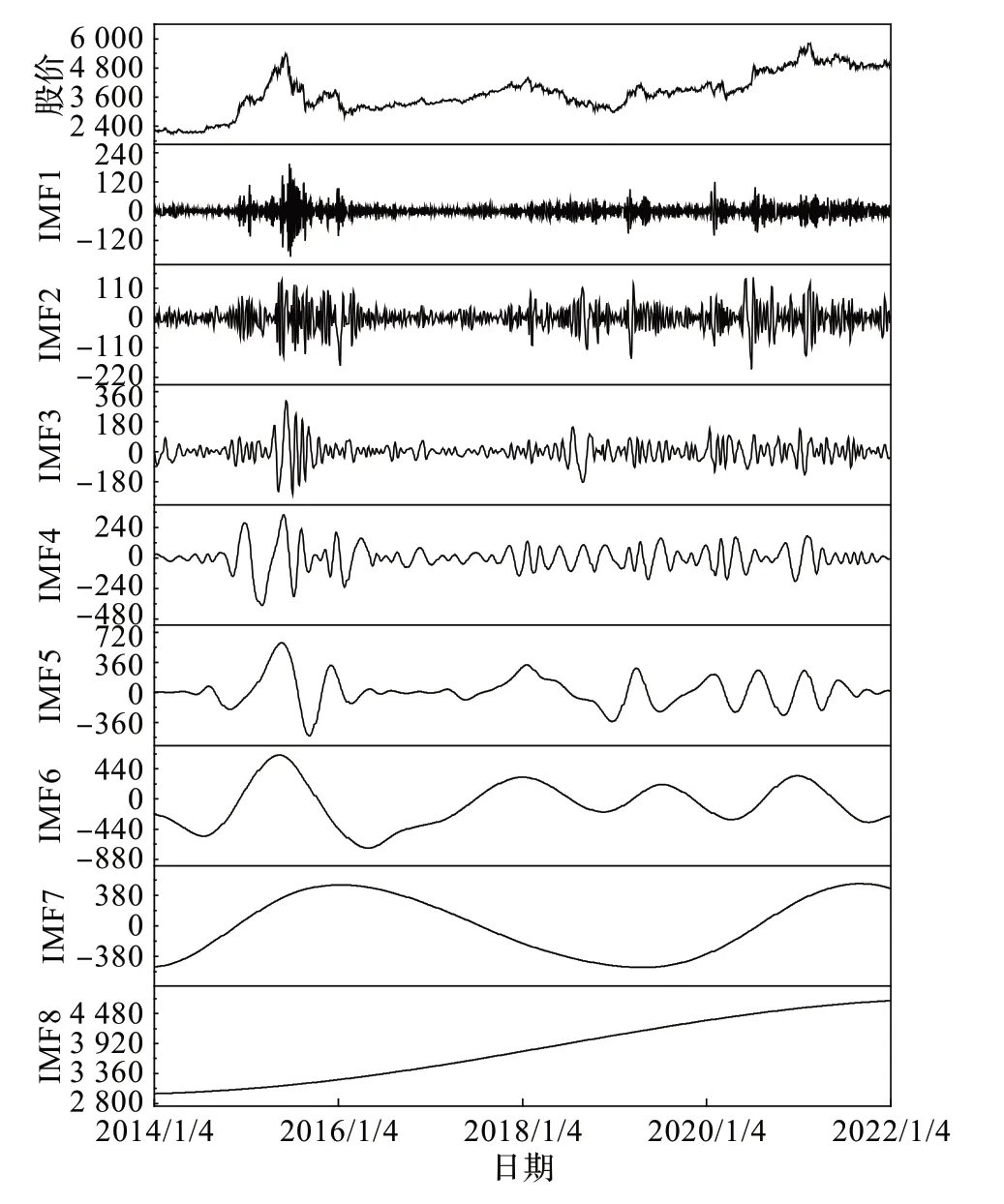

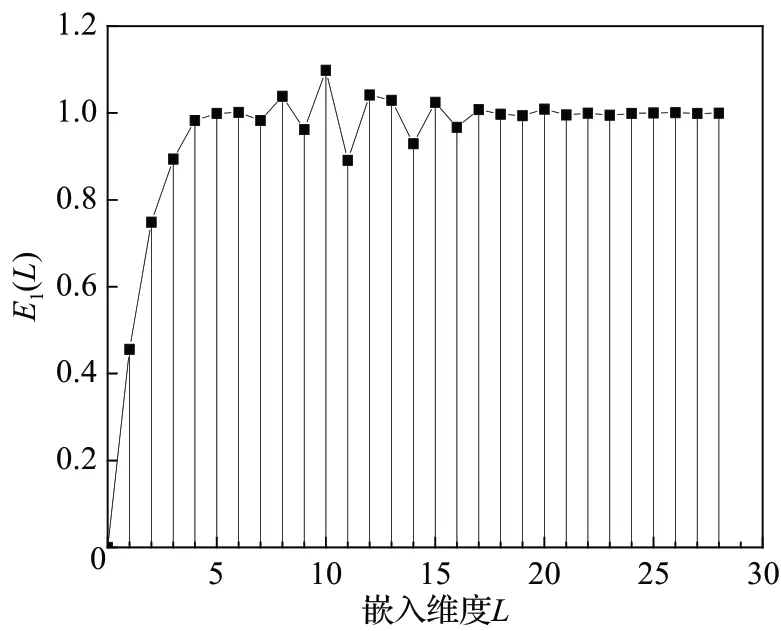
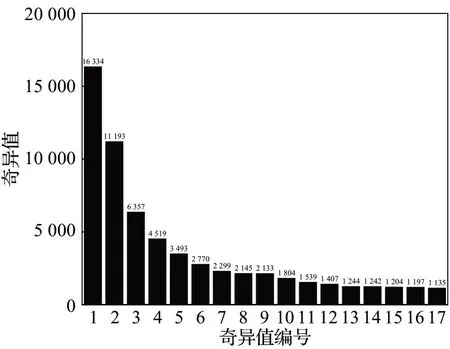
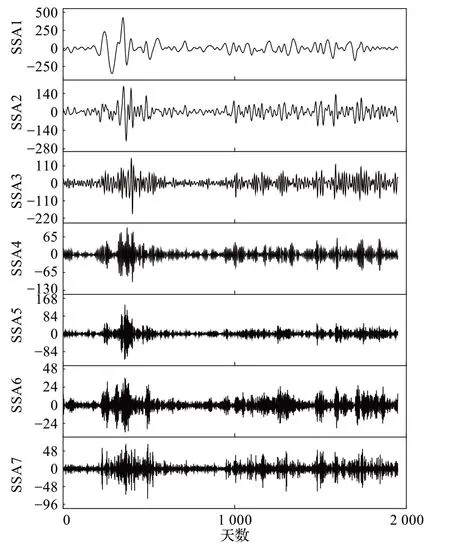
2.3 评价指标
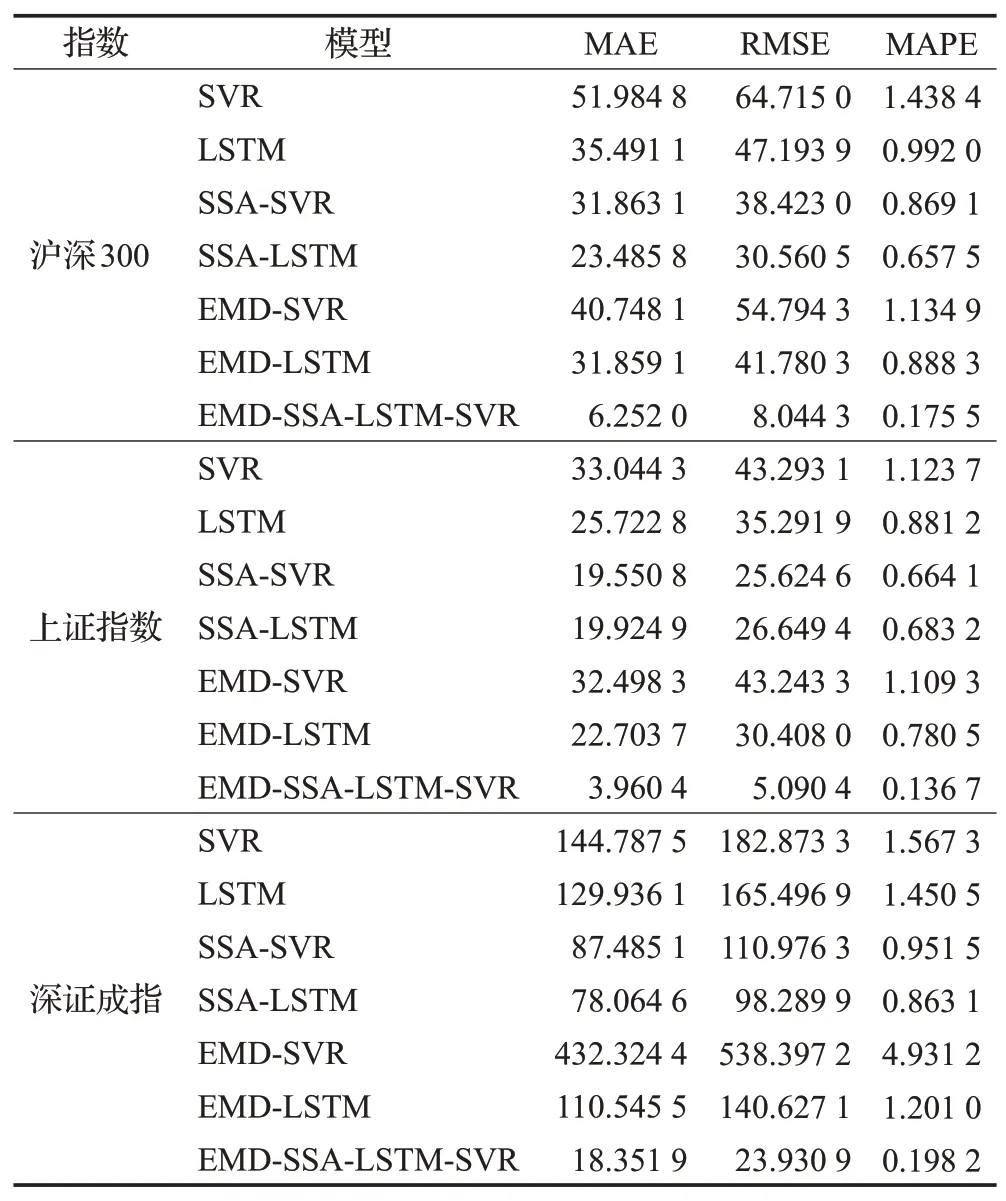
2.4 实证结果





2.5 实验结果分析

3 结束语

