2023年高考之立体几何和空间向量考点解读

■河南省许昌市高中数学胡银伟名师工作室 胡银伟

立体几何涉及两大问题:一是空间基本图形的位置关系,主要包括线线、线面、面面的平行与垂直等;二是度量问题,主要包括点到线、点到面的距离,直线与直线、直线与平面、平面与平面所成的角等。

空间向量是用代数的方法处理立体几何问题的一种重要工具,用定量的计算代替定性的分析,从而避免了一些烦琐的推理论证。利用空间向量的工具性可以解决空间线面的位置关系,空间角、距离及探索性等问题。

下面我们结合2023年高考真题,对立体几何和空间向量的考点进行解读。

考点一 对空间几何体体积的考查

例1(1)(2023年高考全国乙卷理数第8题)已知圆锥PO的底面半径为,O为底面圆心,PA,PB为圆锥的母线,∠AOB=120°,若△PAB的面积等于,则该圆锥的体积为( )。

(2)(2023 年高考全国甲卷文数第10题)在三棱锥P-ABC中,△ABC是边长为2的等边三角形,|PA|=|PB|=2,|PC|=,则该棱锥的体积为( )。

(3)(2023 年新课标全国Ⅰ卷第14 题)在正四棱台ABCD-A1B1C1D1中,|AB|=2,|A1B1|=1,AA1=,则该棱台的体积为____。

命题意图：本题考查圆锥、棱锥、棱台的体积,同时考查了逻辑推理、直观想象及数学运算等核心素养。

解题思路：(1)依题设条件,可利用三角形面积公式先求得圆锥的母线长,再求圆锥的高,根据圆锥的体积公式进行解答。 (2)依题意可证得AB⊥平面PEC,故分割三棱锥为共底面的两个小三棱锥,其高之和为|AB|,得解。(3)结合图像,依次求得|A1O1|,|AO|,|A1M|,再利用棱台的体积公式可得解。

解析：(1)在△AOB中,∠AOB=120°。而|OA|=|OB|=,取AB的中点C,连接OC,PC,则OC⊥AB,PC⊥AB,如图1所示。

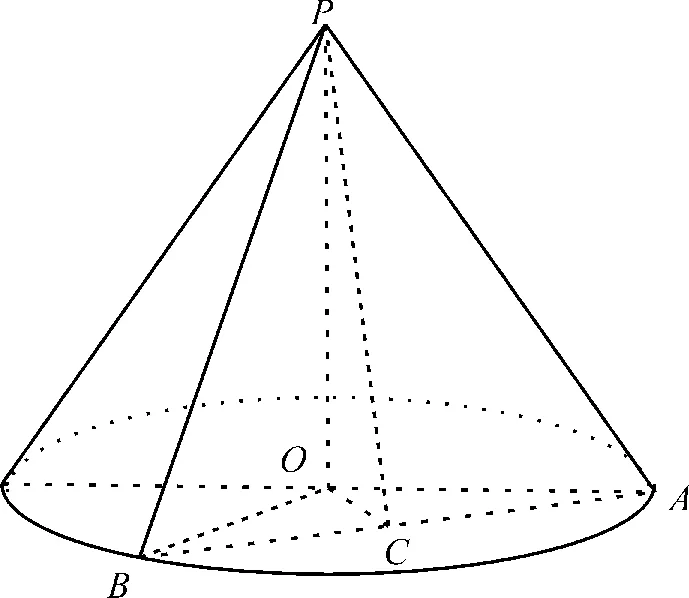
图1

(2)取AB的 中点E,连接PE,CE,如图2所示。

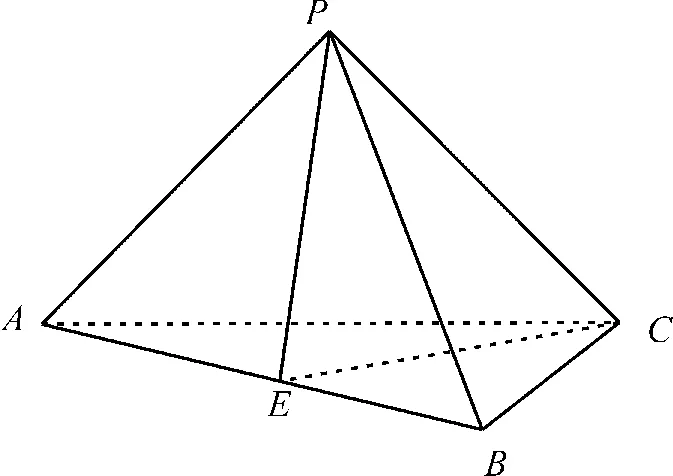
图2

因为△ABC是边长为2 的等边三角形,|PA|=|PB|=2,所 以PE⊥AB,CE⊥AB。

又PE,CE⊂平面PEC,PE∩CE=E,所以AB⊥平面PEC。

(3)如图3,过A1作A1M⊥AC,垂足为M,易知A1M为四棱台ABCD-A1B1C1D1的高。

图3

因为|AB|=2,|A1B1|=1,|AA1|=,所以

考点解读:空间几何体的结构特征是立体几何的基础,空间几何体的表面积和体积是高考的高频考点,多以选填题的形式考查,难度中等或偏上。求几何体体积的常用方法:

考点二 对空间直线与平面位置关系的考查

例2(2023 年高考全国乙卷文数第19 题)如图4,在三棱锥P-ABC中,AB⊥BC,|AB|=2,|BC|BP,AP,BC的中点分别为D,E,O,点F在AC上,且BF⊥AO。

图4

(1)求证:EF//平面ADO;

(2)若∠POF=120°,求三棱锥P-ABC的体积。

命题意图：本题考查空间线面位置关系的证明及几何体体积的计算,考查直观想象、逻辑推理等核心素养。

解题思路：(1)依题设条件,可证得四边形ODEF为平行四边形,再利用线面平行的判定定理进行证明。(2)作出并证明PM为棱锥的高,再利用三棱锥的体积公式直接求解。

又EF⊄平面ADO,DO⊂平面ADO,所以EF//平面ADO。

(2)如图5,过P作PM垂直FO的延长线交于点M。因为|PB|=|PC|,O是BC的中点,所以PO⊥BC。

图5

在Rt△PBO中,|PB|,所以|PO|=

因为AB⊥BC,OF//AB,所 以OF⊥BC。又PO∩OF=O,PO,OF⊂平面POF,所以BC⊥平面POF。

又PM⊂平面POF,所以BC⊥PM。

又BC∩FM=O,BC,FM⊂平面ABC,所以PM⊥平面ABC,即三棱锥P-ABC的高为PM。

因为∠POF=120°,所以∠POM=60°。

考点解读:高考对空间线面位置关系的考查,一是空间线面关系的命题真假的判断,以选填题的形式考查,属于基础题;二是空间线线、线面、面面平行和垂直关系交汇的综合命题,常放在解答题的第一问,属于中档题。平行、垂直关系的证明主要应用转化思想,即通过判定定理、性质定理将线线、线面、面面之间的平行、垂直关系相互转化。

考点三 对空间几何体外接球的考查

例3(1)(2023年高考全国乙卷文数第16题)已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3 的等边三角形,SA⊥平面ABC,则|SA|=____。

(2)(2023 年高考全国甲卷理数第15题)在正方体ABCD-A1B1C1D1中,E,F分别为AB,C1D1的中点,以EF为直径的球的球面与该正方体的棱共有____个公共点。

(3)(2023 年高考全国甲卷文数第16题)在正方体ABCD-A1B1C1D1中,|AB|=4,O为AC1的中点,若该正方体的棱与球O的球面有公共点,则球O的半径的取值范围是_____。

命题意图：本题考查空间几何体的外接球问题,考查直观想象、逻辑推理及数学运算等核心素养。

解题思路：(1)依题意,先由正弦定理求得底面外接圆的半径,再结合直棱柱的外接球及性质进行求解。 (2)根据正方体的对称性知,球心到各棱距离相等,可得解。(3)依题意,当球是正方体的外接球时半径最大,当边长为4的正方形是球的大圆的内接正方形时半径达到最小。

解析：(1)如图6,将三棱锥S-ABC转化为直三棱柱SMN-ABC。设△ABC的外接圆圆心为O1,半径为r,则,可得r=。设三棱锥S-ABC的外接球球心为O,连接OA,OO1,则。因为|OA2|=|OO1|2+|O1A|2,即所以解得|SA|=2。

图6

(2)不妨设正方体的棱长为2,EF的中点为O。分别取CD,CC1的中点G,M,侧面BB1C1C的中心为N,连接FG,EG,OM,ON,MN,如图7。

图7

所以球O与棱CC1相切,球面与棱CC1只有1个交点。

同理,根据正方体的对称性知,其余各棱和球面也只有1 个交点,所以以EF为直径的球面与正方体每条棱的交点总数为12。

(3)设球的半径为R。当球是正方体的外接球时,恰好经过正方体的每个顶点,所求的球的半径最大,若半径变得更大,球会包含正方体,导致球面和棱没有交点,正方体的外接球直径2R'为体对角线长|AC1|=,即,故Rmax=。

如图8,分别取侧棱AA1,BB1,CC1,DD1的中点M,H,G,N,显然四边形MNGH是 边 长 为4 的正方形,且O为正方形MNGH的对角线交点。连接MG,则|MG|=4 2,当球的一个大圆恰好是四边形MNGH的外接圆时,球的半径达到最小,即R的最小值为。

图8

考点解读:球与几何体的切接问题是高考命题的高频考点,常作为客观题中的压轴题。此类问题要求同学们有较强的空间想象能力和准确的计算能力,试题难度较大。解决与球有关的切接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:

考点四 对空间角的考查

角度1 对直线与平面所成的角的考查

例4(2023年高考全国乙卷理数第9题)已知△ABC为等腰直角三角形,AB为斜边,△ABD为等边三角形,若二面角C-ABD为150°,则直线CD与平面ABC所成角的正切值为( )。

命题意图：本题考查直线与平面所成的角及二面角,考查直观想象、逻辑推理的核心素养。

解题思路：依据题设,确定线面角,再利用正弦、余弦定理进行解答。

解析：如图9,取AB的中点E,连接CE,DE。因为△ABC是等腰直角三角形,且AB为斜边,所以CE⊥AB。又△ABD是等边三角形,则DE⊥AB。从而∠CED为二面角CAB-D的平面角,即∠CED=150°。

显 然CE∩DE=E,CE,DE⊂平 面CDE,于是AB⊥平面CDE。又AB⊂平面ABC,所以平面CDE⊥平面ABC。显然平面CDE∩平面ABC=CE,直线CD⊂平面CDE,则直线CD在平面ABC内的射影为直线CE,从而∠DCE为直线CD与平面ABC所成的角。

角度2 对二面角的考查

例5(2023年新课标全国Ⅱ卷第20 题)如 图10,三 棱锥A-BCD中,|DA|= |DB| = |DC|,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点。

图10

(1)证明:BC⊥DA;

(2)点F满足,求二面角D-AB-F的正弦值。

命题意图：本题考查线线垂直及二面角,同时考查逻辑推理、数学运算的核心素养。

解题思路：(1)依题意易证BC⊥平面ADE,从而证得BC⊥DA。(2)由题设可证AE⊥平面BCD,所以以点E为原点,ED,EB,EA所在直线分别为x,y,z轴,建立空间直角坐标系,分别求出平面ABD,ABF的一个法向量,根据二面角的向量公式得所求。

解析：(1)连接AE,DE。因为E为BC的中点,|DB|=|DC|,所以DE⊥BC。①

因为|DA|=|DB|=|DC|,∠ADB=∠ADC=60°,所以△ACD与△ABD均为等边三角形,|AC|=|AB|,从而AE⊥BC。②

由①②知,AE∩DE=E,AE,DE⊂平面ADE,所以BC⊥平面ADE。

而AD⊂平面ADE,所以BC⊥DA。

(2)不妨设|DA|=|DB|=|DC|=2。因为BD⊥CD,所以|BC|=2,|DE|=|AE|=。

所以|AE|2+|DE|2=4=|AD|2,所以AE⊥DE。又因为AE⊥BC,DE∩BC=E,DE,BC⊂平面BCD,所以AE⊥平面BCD。

不妨以点E为原点,ED,EB,EA所在直线分别为x轴,y轴,z轴,建 立空间直角坐标系,如图11所示。

图11

则D(2,0,0),A(0,0,),B(0,0),E(0,0,0)。

设平面DAB与平面ABF的一个法向量分别为n1=(x1,y1,z1),n2=(x2,y2,z2)。

取x1=1,得n1=(1,1,1)。

同理:

取y2=1,得n2=(0,1,1)。

考点解读:利用空间向量求二面角或线面角是高考热点,常以解答题的形式出现,难度中等。对解答题中线面角、二面角问题的求解,或已知线面角、面面角求参数问题,常通过建系,利用空间向量的坐标的方法进行解答,正确求出平面的法向量是解答问题的关键。

考点五 对立体几何综合应用的考查

例6(1)(2023年新课标全国Ⅱ卷第9题)(多选)如图12,已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,|PA|=2,点C在底面圆周上,且二面角P-AC-O为45°,则( )。

图12

A.该圆锥的体积为π

C.|AC|=

D.△PAC的面积为

(2)(2023 年高考全国甲卷理数第11题)已知四棱锥P-ABCD的底面是边长为4的正方形,|PC|=|PD|=3,∠PCA=45°,则△PBC的面积为( )。

命题意图：本题是对立体几何问题综合应用的考查,考查直观想象、逻辑推理及数学建模的核心素养。

解题思路：(1)根据圆锥的体积、侧面积及二面角的知识进行逐项判断。(2)思路一:先 依 次 证 得△PDO≅△PCO,△PDB≅△PCA,得|PA|=|PB|。再在△PAC中利用余弦定理求得PA,从而得PB,然后在△PBC中利用余弦定理与三角形面积公式得所求。思路二:先在△PAC中利用余弦定理求得PA,cos∠PCB的值,从而求得,利用空间向量的数量积运算与余弦定理得到关于PB,∠BPD的方程组,从而求得PB的值,然后在△PBC中利用余弦定理与三角形面积公式即可得所求。

(2)解法一:连接AC,BD交于O,连接PO,则O为AC,BD的中点,如图13所示。

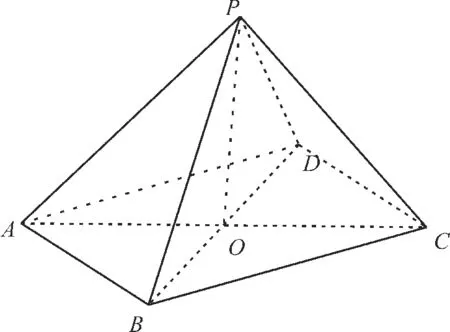
图13

因为底面ABCD为正方形,|AB|=4,所以|AC|=|BD|=,则|DO|=|CO|=。

又|PC|=|PD|=3,|PO|=|OP|,所以△PDO≅△PCO,∠PDO=∠PCO。

又|PC|=|PD|=3,|AC|=|BD|=,所以△PDB≅△PCA,|PA|=|PB|。

在△PAC中,|PC|=3,|AC|=,∠PCA=45°,由余弦定理得,|PA|2=|AC|2+|PC|2-2|AC|·|PC|cos∠PCA=32+9-2××3×=17,故|PA|=。

解法二:连接AC,BD交于O,连接PO,则O为AC,BD的中点,如图13所示。

因为底面ABCD为正方形,|AB|=4,所以|AC|=|BD|=4。

又在△PBD中,|BD|2=|PB|2+|PD|2-2|PB|·|PD|cos∠BPD,即32=m2+9-6mcosθ。

则m2-6mcosθ-23=0。②

故选C。

考点解读:高考立体几何试题中每年都有1-2道选填题,常涉及几何体的体积,内切、外接球,截面,动点轨迹,最值及探索性问题等,试题灵活且考查的知识点综合性强,能够很好地考查同学们知识的综合应用能力及分析问题、解决问题的能力。