椭圆截面弹体侵彻性能的影响因素分析*

刘均伟，张先锋，刘 闯，王佳敏，熊 玮，谈梦婷，肖 川

（1.南京理工大学机械工程学院，江苏 南京 210094；2.北方工业集团公司，北京 100053）

对于滑翔式高超声速飞行器而言，由于其气动外形要求，有效载荷空间一般呈现为不对称椭圆、不对称菱形、舌形和梯形等异形截面形状。椭圆截面弹体以其对平台适应性好、有效载荷空间利用率高等优点，成为滑翔式高超声速武器平台的首选方案。诸多学者在椭圆截面弹体对目标的侵彻作用机理方面已开展了大量研究工作[1-15]。王文杰等[1]开展了椭圆截面弹体侵彻砂浆靶试验，通过分析弹靶的变形和破坏，发现弹体横截面长轴端点附近区域受力更大，且弹体长短轴参数的改变对侵彻性能影响较显著。Dong 等[2-3]开展了一系列椭圆截面弹体侵彻半无限厚混凝土靶试验，弹体的长短轴比分别为1.5 和2.0。试验数据表明，椭圆截面弹体在700～1 000 m/s 的撞击速度范围内具有良好的侵彻性能和弹道稳定性。同时，通过数值模拟研究了椭圆截面弹体侵彻混凝土的受力特性，结果表明，在相同侵彻速度下，弹体头部的法向应力从短轴向长轴逐渐增大。王浩等[4-5]开展了椭圆截面弹体正贯穿加筋板试验研究，获得了椭圆截面弹体剩余速度和弹道极限速度的预测公式，得出了随着椭圆截面弹体长短轴比增大，靶板的弹道极限速度近似线性增大的结论。进一步地，田泽等[6]基于王浩的试验结果，采用能量守恒和虚功原理分阶段分析弹体受力特征，建立了弹体姿态偏转理论模型，并分析了弹体撞击速度、初始倾角、质心位置、弹体翻滚角及截面长短轴比等参数对椭圆变截面弹体姿态偏转的影响。邓希旻等[7]开展了上下非对称结构异形弹体正/斜贯穿多层间隔921A 薄钢板实验，基于Abaqus/Explicit、VUMAT 和Python子程序分析了靶体的能量耗散情况和损伤机理。在弹体侵彻阻力方面，Dai 等[8]基于空腔膨胀模型，系统分析了弹体结构参数对椭圆截面弹体侵彻性能的影响，并给出了封闭形式的弹体深度预测公式。刘子豪等[9]通过数值模拟、理论推导与试验研究相结合的方法，对椭圆截面弹体高速侵彻混凝土特性进行了研究，得出在侵彻速度相同时，弹体侵彻深度随着弹体长短轴比的增大而增大。Liu 等[10-11]开展了椭圆截面弹体侵彻半无限混凝土靶和金属靶试验研究，分析了弹体侵彻阻力与弹靶参数的关系，建立了考虑截面形状影响的阻力修正函数。Ma 等[12]基于修正的空腔膨胀模型，建立了非对称椭圆弹体斜侵彻有限厚金属靶弹道偏转模型，结果表明，通过合理设计弹体结构，非对称椭圆截面弹体可以保持与圆形截面弹体相同的侵彻能力。魏海洋等[13]研究了椭圆截面弹体对金属厚靶的侵彻弹道规律，基于空腔膨胀理论和局部相互作用模型，建立了椭圆截面弹体侵彻弹道模型，结果表明，椭圆截面弹体侵彻弹道稳定性随长短轴比的增大而变弱，最优长短轴比为1.0。谭远深等[14]基于152 mm 口径轻气炮开展了椭圆截面弹体反弹道侵彻试验研究，并结合数值模拟结果建立了椭圆截面侵彻弹体弯曲结构响应计算模型。刘均伟等[15]开展了3 种不同椭圆截面弹体正贯穿有限厚2A12 铝板的试验与数值模拟，结果表明，弹体长短轴比对靶体破坏形貌和响应特性影响显著，椭圆截面弹体侵彻作用下靶体呈现非对称破坏。

综上所述，针对椭圆截面弹体侵彻各类介质靶体，主要研究集中于弹体剩余速度、侵彻深度和弹道稳定性方面，取得了一定的研究成果。但关于圆形和椭圆截面弹体侵彻性能孰优孰劣这一基本问题尚不明确，亟待分析、明确影响椭圆截面弹体侵彻性能的主要因素。

本文中，首先，设计并开展圆锥和椭圆锥压头的准静态深压痕试验，以评估在不考虑动态效应时截面形状对侵彻阻力的影响；然后，开展椭圆截面弹体正侵彻2A12 厚铝靶试验，分析靶体的破坏形貌及弹体侵彻深度；最后，结合团队前期研究得到的阻力函数修正系数[10]和空腔膨胀模型，建立弹体侵彻动力学模型，并系统讨论截面形状和头部曲径比对弹体侵彻性能的影响。

1 椭圆锥压头压痕试验

圆形和椭圆截面弹体对半无限靶的侵彻性能优劣尚未有明确定论，弹体侵彻时，靶体阻力和弹体结构综合决定了弹体的侵彻性能。由于两者的耦合作用，在动态侵彻试验中很难对其中的单一因素进行定量分析。众所周知，深压痕试验[16-20]可以反映不同材料对刚性弹体的侵彻阻力。因此，为评估在不考虑动态效应时截面长短轴比对侵彻阻力的影响，开展了圆锥和椭圆锥压头深压痕试验，通过压缩试验机记录的力-位移曲线定量分析不同截面形状压头之间的阻力差异。该部分工作可认为是获得给定目标对刚性侵彻弹体施加的侵彻阻力的基础。

1.1 试验方案

3 种类型压头（CC1、EC1 和EC2）的长短轴比分别为1.00、1.50 和2.00，几何参数如表1 所示，其中a和b分别为压头截面的长半轴长和短半轴长，β 为弹体长短轴比，定义为β=a/b。圆锥压头的直径为8.00 mm，锥角为21°。椭圆锥压头保持与圆锥压头相同的最大横截面面积、长度和质量，但其截面形状为椭圆。需要说明的是，为了避免压入过程中侧壁摩擦对试验结果的影响，压头直径比压头杆部直径大0.10 mm，如图1 所示。压头材料为30CrMnSiNi2A，屈服强度约为1.4 GPa，远高于2A12 铝合金试样的屈服强度。2A12 铝合金试样直径约为100 mm，高度为80 mm。利用压缩试验机进行静态深压痕试验，记录机器工作时间、压头受力及其位移，控制压缩试验机的速率为0.5 mm/min。压痕试验中压头安装方式及布置如图2 所示，通过特定的套筒保持压头的同轴度，确保垂直压入试样。

图1 CC1 压头的设计Fig.1 CC1 indenter drawing

图2 压头安装方式及现场布局Fig.2 Installation and layout of the indenter

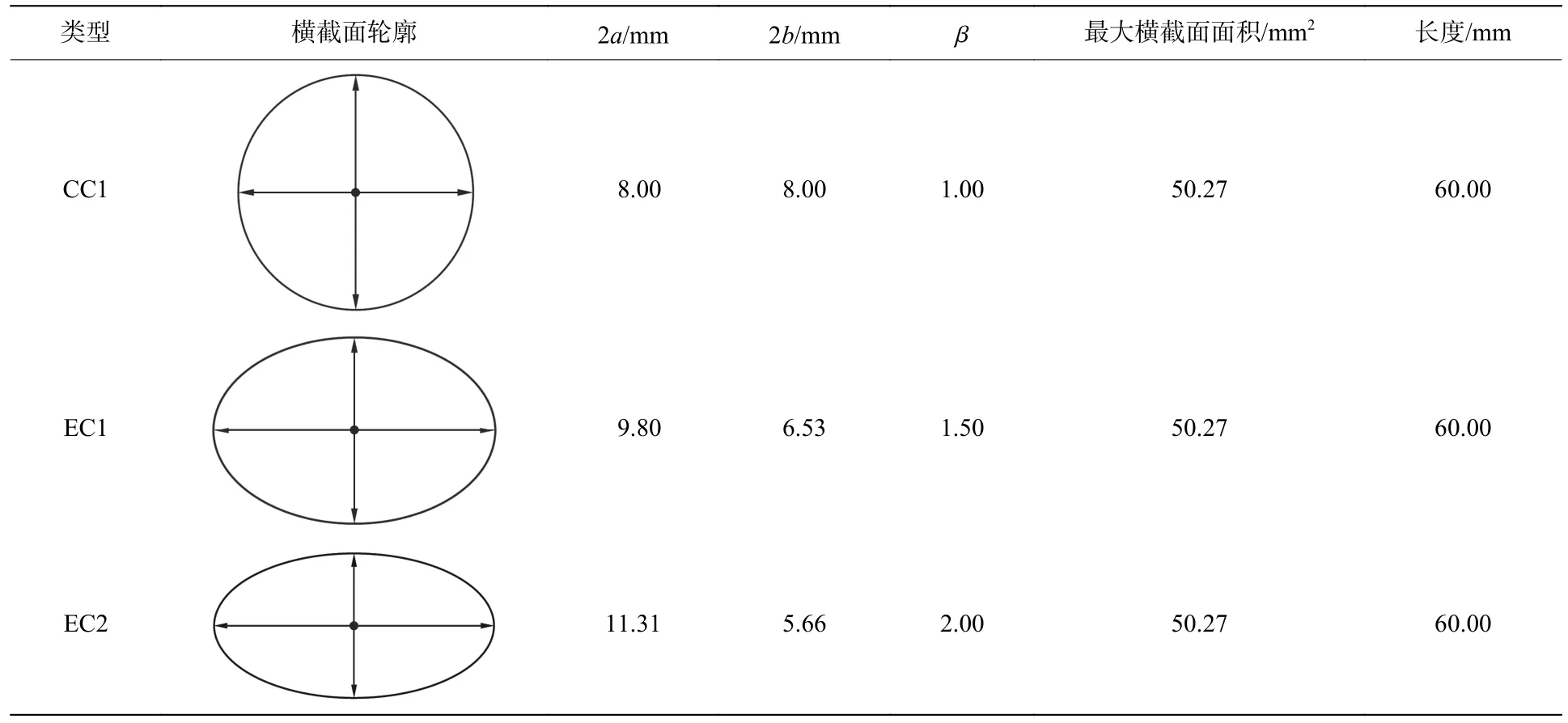
表1 圆锥和椭圆锥压头的几何参数Table 1 Main geometric parameters of circular and elliptical cross-section conical indenters

1.2 试验结果与分析

共进行6 次压痕试验，得到的力-位移时间曲线如图3 所示。可以看出，压痕试验的所有曲线都遵循3 个明显的阶段，即图中采用蓝色虚线划分的区域。第1 阶段是压头头部接触目标直至完全嵌入目标的过程，该过程中曲线类似于二次函数，此时压入深度约为15 mm。第2 阶段则由于压头持续地贯入目标，压头的阻力仍在缓慢增加，力与位移的关系更接近线性。第3 阶段为稳定阶段，随着位移的增加，力基本不再变化。这与文献[19-20]报道的曲线略有不同，产生差异的原因是本文中的压头直径比压头杆部直径大0.10 mm，减弱了压入过程中侧壁摩擦对试验结果的影响。

图3 压痕试验测量的力-位移曲线Fig.3 Force-distance record in the deep indentation test

此外，从图3 中可以看出，第2 条蓝色虚线位于32 mm 处，约为圆锥压头直径的4 倍。意味着对于圆锥压头，当压入深度超过32 mm 时，力逐渐趋于稳定。而椭圆锥压头的边界线则超过32 mm，这表明椭圆锥压头需要贯入更大的深度才能达到稳定的阻力。

从图3(a)～(c)可以看出，3 种压头的深压痕试验数据均具有良好的重复性，微小的差异可以归因于试验中2A12 铝样品特性的差异。图3(d)对比了不同长短轴比的椭圆锥压头的力-位移曲线。长短轴比β=2.00 的EC2 压头始终保持在曲线顶端，其次是β=1.50 的EC1 压头，最后是β=1.00 的CC1 压头。此外，2A12 铝合金试样对3 种压头的作用力分别达到约41.24、40.32 和37.45 KN 的恒定水平。这意味着β=1.50 的椭圆锥压头所需阻力比圆锥压头大6.8%，而β=2.00 的椭圆锥压头阻力则大10.1%。

Rosenberg 等[21-22]通过分析刚性弹体侵彻铝靶的试验数据及其数值模拟结果，指出在阈值速度下弹体侵彻阻力表现为靶体强度项，并与弹体结构等若干因素相关联。深压痕试验可以反映不同材料对刚性弹体的侵彻阻力，因此利用深压痕试验获得的数据来评价刚性弹体在阈值速度下的侵彻性能是可行的。可以合理推测，当质量、长度等参数一致时，长短轴比较大的椭圆截面弹体在阈值速度下侵彻性能较差。当然，静态压痕试验和侵彻试验下材料应变率差异很大，且由于铝靶强度是率相关的，即使不考虑惯性项阻力，两种情况下材料侵彻阻力一定会存在部分差异，但仍可对认识截面形状对侵彻阻力的影响起到一定帮助。另一方面，截面形状所影响的靶体侵彻阻力只是决定弹体侵彻性能的部分因素，弹体结构对侵彻性能的影响不可忽略。因此，将通过开展椭圆截面弹体正侵彻2A12 厚铝靶试验，综合分析弹体截面长短轴比和头部曲径比对侵彻性能的影响。

2 椭圆截面弹体正侵彻2A12 厚铝靶试验与理论模型

2.1 试验弹体与靶体

为分析弹体撞击速度和截面形状对弹体侵彻性能的影响，开展了椭圆截面弹体正侵彻2A12 厚铝靶试验。弹体材料为30CrMnSiNi2A 高强度钢，经淬火处理后洛氏硬度HRC 为42，屈服强度约为1.2 GPa。试验中使用了2 种椭圆截面弹体（E1 和E2 弹体）和1 种圆形截面弹体（C1 弹体），3 种弹体的结构参数如图4 和表2 所示。表中：L为弹体头部长度，m为弹体质量，rCRH为头部曲径比。应当指出，对于椭圆截面弹体，严格来讲并没有头部曲径比的概念。椭圆截面弹体的rCRH与弹体方位角呈正相关，沿圆周从短轴方向到长轴方向逐渐减小。因此，在表2 中列出了弹体在短轴方向上的rCRH，其他方向上的rCRH则可以根据弹体的几何方程计算。为保证侵彻后弹体的完整性，靶体选用塑性好、强度较低的2A12 铝合金。同时，为减小边界效应对侵彻过程的影响，靶体直径选取为300 mm，厚度为400 mm，为弹体直径的13 倍，如图5所示。一般而言，在该尺寸下可以忽略靶体侧面和背面边界效应对弹体侵彻过程的影响。

图4 试验弹体Fig.4 Projectiles used in the test

图5 试验靶体Fig.5 Targets used in the test

表2 圆形和椭圆截面弹体的主要结构参数Table 2 Main parameters of circular and elliptical cross-section projectiles

图6 为试验现场布置，采用高速摄像机观察弹体飞行姿态，同时2 个平面镜分别放置于靶前和靶后弹体运动轨迹的正下方，与平面呈45°夹角，通过测量并分析弹体和平面镜中弹体的位置变化，得到弹体的速度、运动轨迹和姿态。

图6 试验示意图和现场布局Fig.6 Layout of penetration test

2.2 侵彻试验结果

本次试验共计8 发，其中C1 弹体2 发，E1 弹体3 发，E2 弹体3 发，通过调整发射药量控制弹体速度在400～800 m/s 范围内。图7 给出了E2-2 弹体的飞行姿态，根据高速摄影以及平面镜可以核定出弹体的着靶姿态和初始撞击速度，试验结果统计如表3 所示，表中：v0为弹体初始撞击速度，Pe为弹体侵彻深度。从表3 可以看出，3 组对照试验中各弹体初始撞击速度差异较小，具有一定的对比性；弹体俯仰角最大值为0.53°，偏航角最大为2.79°，基本满足正侵彻条件。图8 给出了弹体侵彻前后的对比，可以看出，弹体长度和形状无明显变化，仅表面有一定的摩擦痕迹。因此，椭圆截面弹体正侵彻2A12 厚铝靶过程可视为刚体侵彻。

图7 E2-2 弹体飞行姿态Fig.7 Flying attitude of the E2-2 projectile

图8 试验前后弹体对比Fig.8 Comparison of projectiles before and after tests

表3 弹体侵彻2A12 厚铝靶试验结果统计Table 3 Test results of projectiles penetrating 2A12 thick aluminum targets

2.3 椭圆截面弹体侵彻动力学模型

球形空腔膨胀（sphere cavity expansion，SCE）模型常用于计算刚性弹体侵彻各类介质靶体的侵彻深度/剩余速度[23-32]。因此，结合Liu 等[10]研究得到的阻力函数修正系数kr和空腔膨胀模型，建立考虑截面形状影响的弹体侵彻动力学模型。图9 给出了椭圆截面弹体的头部几何形状，其中a1和b1分别为弹体的长半轴和短半轴长，x0、y0和z0为弹体在3 个轴线的坐标，r1为弹体最大椭圆横截面的极径，r0为任意椭圆横截面的极径，Rs为头部任意点处的曲率半径，θ0为任意卵形曲线与x0Oy0平面之间的方位角，χ0为卵形头部表面的外法线向量与弹轴之间的夹角，η0为弹体表面微元投影至x0Oy0平面上与x0轴的夹角。

图9 椭圆截面弹体的头部几何形状示意图Fig.9 Nose geometry diagram of the elliptical cross-section projectile

式中：σY、ρt、Et和nt分别为靶体的压缩屈服强度、密度、杨氏模量和应变硬化指数；kr1和kr2为无量纲系数，kr2=1.5；δ 为积分变量；K为积分常数。

进一步，椭圆截面弹体头部的微元所受应力需要考虑应力分布的不均匀性，因此椭圆截面弹体头部表面应力σn可由传统球形空腔膨胀所得应力σr，即式(4)，并结合阻力函数修正系数kr表示：

阻力函数修正系数kr的函数表达式为：

式中：Ar和Br为常数，受椭圆空腔长短轴比、材料特性等影响。

图10 给出了圆形和椭圆空腔的阻力函数修正系数kr随角度的变化情况。可以看出，圆形空腔的修正系数恒为1，而椭圆空腔的修正系数沿着短轴方向至长轴方向逐渐增大，类似于正弦分布。

图10 阻力函数修正系数Fig.10 Correction coefficient for resistance function

弹体表面径向应力确定后，弹体轴向所受的阻力可以通过式(7)对弹体头部微元Sr积分获得：

当曲面积分转化为二重积分时，式(9)可表示为：

3 椭圆截面弹体侵彻动力学模型验证及影响因素分析

3.1 模型可靠性验证

表4 为弹体侵彻深度计算结果与试验结果的对比，可以看出，理论计算结果与试验结果吻合较好，误差在15%以内。对比分析传统球形空腔膨胀模型和本文中模型计算结果与试验结果的误差可知，本文中考虑椭圆截面形状的理论模型计算结果误差更小，更能反映弹靶接触时真实的受力状况。图11 给出了弹体侵彻深度计算结果与试验结果的对比情况。可以看出，无论是传统球形空腔膨胀模型，还是本文中考虑椭圆截面形状的理论模型计算结果，从侵彻性能来看，均为E2 弹体的侵彻性能最优，其次为C1 弹体，E1 弹体的侵彻性能最差。对于圆形截面弹体，由于阻力函数修正系数kr恒为1，本文中模型与传统球形空腔膨胀模型的计算结果一致，2 条曲线完全重合；而对于E1 和E2 两种椭圆截面弹体，本文中模型计算结果均在传统球形空腔膨胀模型计算结果之下，表明考虑截面形状的影响后，椭圆截面弹体的侵彻性能有所下降。

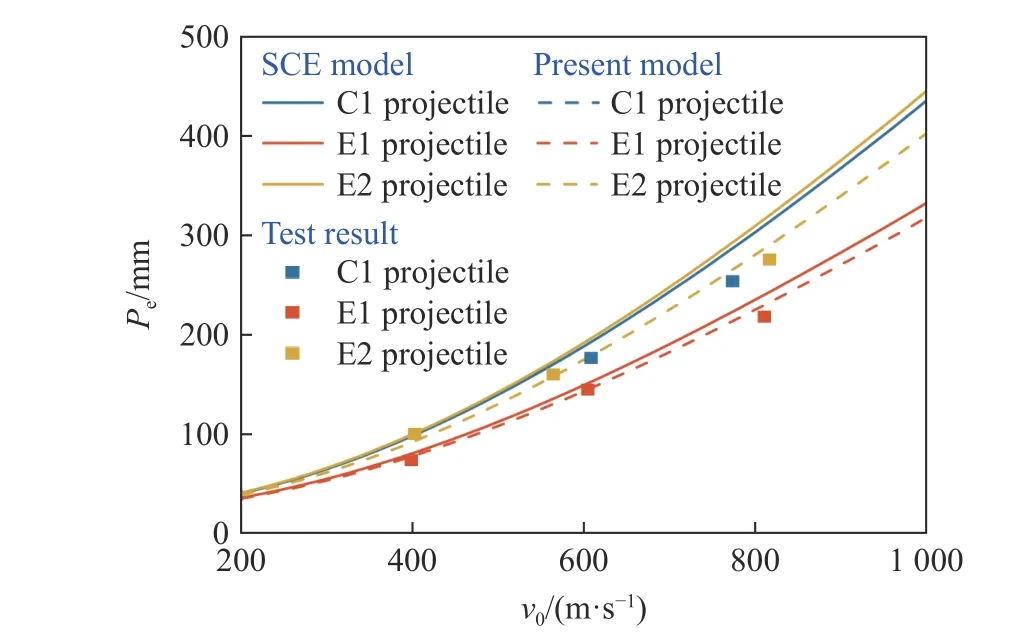
图11 理论模型计算结果与试验结果的对比Fig.11 Comparison of the theoretical model calculation results with test results

表4 弹体侵彻深度计算结果与试验结果的误差Table 4 Deviation of penetration depth between calculation results and test results

进一步对比传统球形空腔膨胀模型计算的C1 和E2 弹体的侵彻深度随弹体撞击速度的曲线可知，由于具有相同的截面面积，因此采用传统球形空腔膨胀模型计算的两者曲线基本一致，而具有较大横截面面积的E1 弹体的侵彻性能低于C1 和E2 弹体，这表明最大横截面面积是衡量弹体侵彻性能的一大因素。然而，传统球形空腔膨胀模型计算的E1 和E2 弹体的侵彻深度相较于试验结果偏大，而考虑椭圆截面对应力分布的影响情况，即在理论模型中加入kr后，侵彻深度的计算结果更接近于试验结果，这意味着截面形状对弹体侵彻性的影响同样不可忽略。

3.2 弹体长短轴比对侵彻性能的影响

椭圆与圆形截面弹体之间最显著的差异是其截面长短轴比不同。为排除曲径比对侵彻性能的影响，设计了长短轴比分别为1.00、1.25、1.50、1.75 和2.00 的5 种椭圆锥弹体，弹体结构参数如表5 所示。除长短轴比外，5 种弹体的质量、长度和最大横截面面积均一致。图12 给出了撞击速度在200～1 000 m/s时5 种弹体的侵彻深度。可以看出，在相同撞击速度下，长短轴比越大的弹体侵彻深度越低。具体而言，长短轴比为2.00 的椭圆锥弹体的侵彻深度比长短轴比为1.00 的圆锥弹体低约13%。

图12 不同长短轴比下侵彻深度与撞击速度的关系Fig.12 Relationships between penetration depth and impact velocity at different major-to-minor axis length ratios

表5 5 种椭圆锥弹体结构的质量参数Table 5 Main parameters of five typical elliptical cone projectiles

为分析侵彻性能差异的原因，提取撞击速度为800 m/s 时5 种弹体典型截面沿周向的径向应力分布，截面位置分别为距弹尖L/3 和2L/3 处。阻力函数修正系数kr如图13 所示，可以看出，椭圆锥弹体的径向应力分布与圆锥弹体明显不同，呈现出从短轴方向到长轴方向逐渐增大的趋势，类似于正弦分布。然而，椭圆锥的径向应力分布曲线并非严格按照基准线（kr=1）对称。图13 中曲线所包围的面积即该截面所提供的弹体阻力。5 种弹体的曲线积分面积与圆锥弹体曲线积分面积的比值分别为1.00、1.02、1.06、1.12 和1.19。这说明椭圆截面影响了弹体的受力分布，导致侵彻阻力增大，且增加比例随着截面长短轴比的增大而增大。

图13 不同长短轴比弹体头部的应力分布特性Fig.13 Stress distribution characteristics of the projectile noses at different major-to-minor axis length ratios

实际上，尖卵形弹体的侵彻性能受到多个因素的影响。当弹体最大横截面面积和头部长度保持一致时，长短轴比和头部曲径比会协同变化。长短轴比影响弹体不同截面的径向应力分布，但这仅是侵彻阻力的基础。在计算侵彻阻力时，需要对弹体表面微元进行曲面积分，其中弹体头部表面的外法线向量和弹轴之间的角度对积分值的影响是不可忽略的，而这与弹体头部曲径比息息相关。

3.3 弹体头部曲径比对侵彻性能的影响

圆形截面弹体的侵彻性能很大程度上取决于头部曲径比。Frew 等[32]的研究结果表明，头部曲径比较大的圆形截面弹体具有更好的侵彻性能。为研究不同头部曲径比下椭圆截面弹体的侵彻性能，设计了5 种典型椭圆截面弹体，其结构参数如表6 所示。为控制头部曲径比的大小，ECS-4 和ECS-5 弹体的头部长度略短于前3 种弹体，但5 种弹体的质量、最大横截面面积和长度均保持一致。同时，需要注意的是，表中标注的为尖卵形弹体短轴方向的头部曲径比。

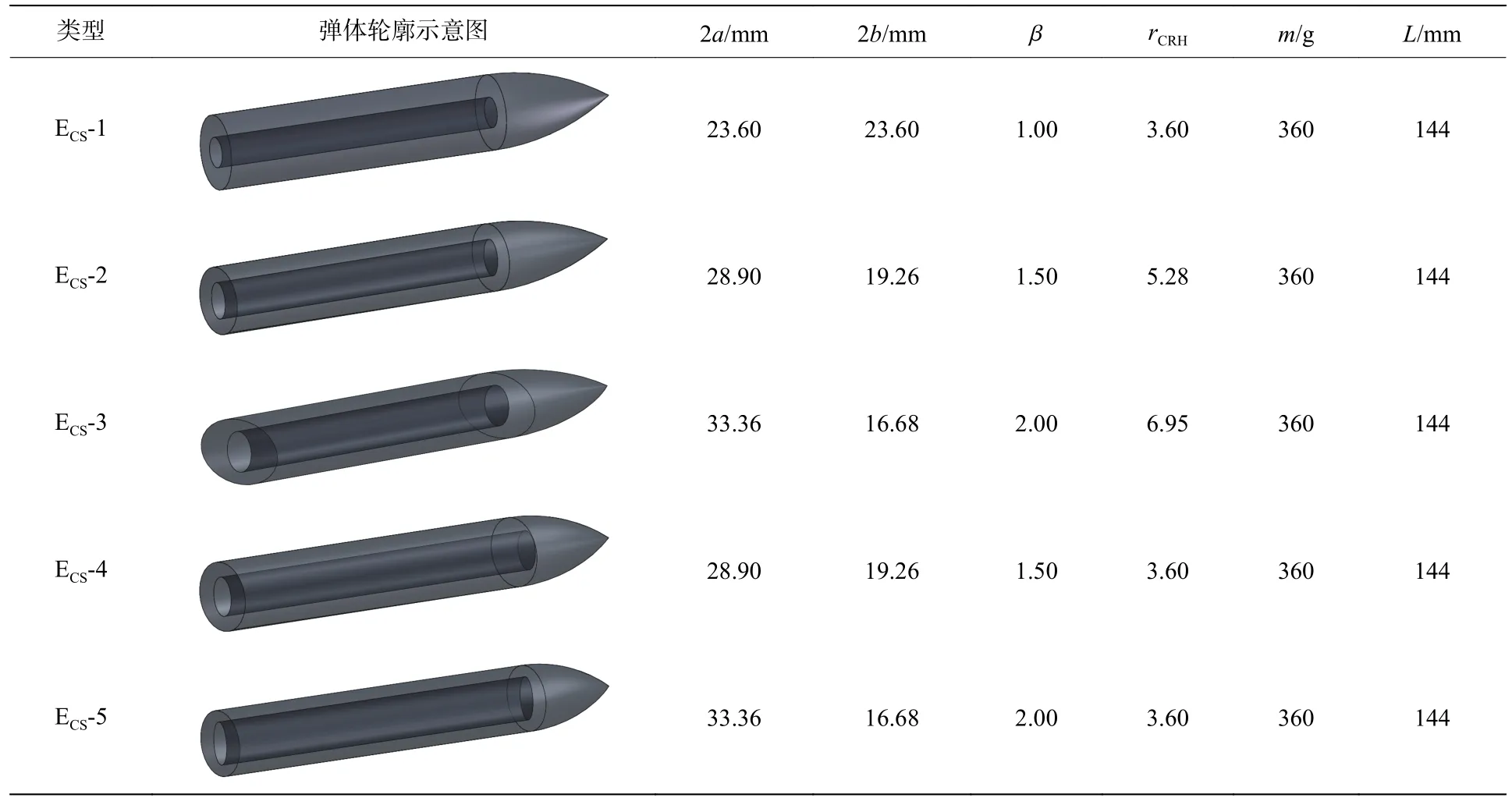
表6 5 种椭圆截面弹体结构的质量参数Table 6 Main parameters of five typical elliptical cross-section projectiles

图14 给出了5 种弹体侵彻深度随撞击速度的变化曲线。从图14 可以看出，2 个对照组（ECS-2 和ECS-4、ECS-3 和ECS-5）表现出相似的规律，即具有相同长短轴比但头部曲径比更小的ECS-4 和ECS-5 弹体的侵彻性能分别略低于ECS-2 和ECS-3 弹体，这意味着对于尖卵形椭圆截面弹体而言，头部曲径比减小降低了弹体的侵彻性能。

图14 头部曲径比和长短轴比对侵彻深度的影响Fig.14 Influence of rCRH and β on penetration depth

此外，相对于ECS-3 和ECS-5 弹体，ECS-1 弹体具有相同的头部曲径比和更小的阻力函数修正系数，因此其侵彻性能优于ECS-3 和ECS-5 弹体。然而，相对于ECS-2 和ECS-3 弹体，ECS-1 弹体在头部曲径比方面处于劣势，而从图14 中可以看到，ECS-1 弹体侵彻性能更优异。这说明在长短轴比1～2 的范围内，截面形状对侵彻性能的减弱可能强于头部曲径比对侵彻性能的增益。综合上述分析可知，当弹体截面面积相当且各横截面保持长短轴比不变时，圆形截面弹体的侵彻性能最优，椭圆截面弹体侵彻性能随着截面长短轴比的增大和头部曲径比的减小而降低。

4 结 论

开展了圆锥和椭圆锥压头的准静态深压痕试验和椭圆截面弹体以400～800 m/s 撞击速度正侵彻2A12 厚铝靶试验，获得了椭圆锥压头的静阻力和椭圆截面弹体侵彻性能的对比结果。结合阻力函数修正系数kr和球形空腔膨胀模型，建立了弹体侵彻动力学模型，并系统讨论了截面形状和头部曲径比对弹体侵彻性能的影响，得出以下主要结论。

(1) 准静态深压痕试验表明，长短轴比更大的椭圆锥压头贯入材料时所受的阻力更大。具体而言，β=1.50 和β=2.00 的椭圆锥压头所需阻力比圆形截面压头分别大6.8%和10.1%。

(2) 结合阻力函数修正系数kr建立的考虑截面形状影响的椭圆截面弹体侵彻动力学模型的计算结果与试验结果的最大相对误差为15%，在侵彻深度预测精度方面优于传统球形空腔膨胀模型。

(3) 当弹体截面面积相当，且各横截面保持长短轴比不变时，圆形截面弹体具有最优的侵彻性能，椭圆截面弹体的侵彻性能随着截面长短轴比的增大和头部曲径比的减小而降低。