多层级装配作业车间分批调度算法设计与分析
钟宏扬,刘建军,黎英杰,陈庆新
(广东工业大学 广东省计算机集成制造系统重点实验室,广东 广州 510006)
作业车间调度问题 (job shop scheduling problem,JSP) 是一类具有工程应用背景的强NP难问题,传统的作业车间调度通常假设加工工件之间完全相互独立,加工工件的所有工序完工以后即视为可交付[1]。近年来,以客户为导向的多品种小批量生产方式兴起,产品的多元化装配结构使得装配工序调度复杂化,因此装配作业车间调度问题 (assembly job shop scheduling problem,AJSP) 也成为JSP问题的一类更具现实意义的拓展研究内容[2-4]。
装配作业车间包括加工和装配两个阶段,工序顺序与装配结构的强关联耦合约束为双阶段的调度计划提出了更多的协同需求[5]。当前AJSP研究大多集中在全局性齐套的装配,即假定产品的所有零部件齐套后直接进行总装作业,如文献[6]是在产品所有关联装配任务都完工后,附加一定的装配工期后即表示产品为完工,并不涉及具体装配资源的调度。但实际生产中产品也存在渐增性齐套的装配结构,关联零件先通过部装组成部件后,待部件齐套后再执行总装[7-8]。产品存在差异化的装配层次特征,加之多产品并行生产的特点,为装配资源调度提出了更多的挑战。
另一方面,在经典的JSP与AJSP问题中,加工任务被视为一个整体不可拆分。整批流转加工的方式虽然可以减少工序的准备时间,但也降低了车间物料运输的流动性,增加了订单在高负载强度生产环境下的拖期风险。对加工任务进行合理批量划分,可以促使子批交叠并行生产,进而提升车间的设备利用率,缩短生产周期[9-11]。允许对加工任务进行分批生产与传输的问题属于分批调度优化问题[12]。分批调度涉及批量划分和排序优化两个子问题,批量划分对后续排序优化效果奠定基础,故而需要全局性较好的算法来确保分批结果的优度。已有的装配作业分批优化算法大多数面向全局性齐套需求[13-14],在渐增性齐套的生产制约关系下,经典的遗传编码与进化操作难以适用。本文以最小化产品的拖期成本与库存持有成本之和为优化目标,构建一套基于改进性遗传算法与高效作业分派规则相耦合的分步式求解框架。通过仿真实验验证该算法在多层级装配作业车间调度问题的有效性,并评估与分析所提算法对不同树状结构产品的调度性能。
1 问题描述
装配作业车间所生产的产品根据客户要求,在需求数量、装配结构与工艺上都有不同程度的差异。如图1所示,装配作业车间的生产包括加工与装配两个阶段,故其调度涉及加工阶段与装配阶段的生产资源。各个装配层级部件/组件的装配工序需要等待直属关联零部件齐套以后方可执行。准时交付水平成为衡量MTO (make-to-order) 型企业竞争力的重要指标,基于文献[15]提出的最小化拖期与库存持有成本之和的优化目标,产品的交付性能与车间的库存持有成本都受制于其下属关联任务加工进度的协同性,而渐增性齐套装配中的库存持有成本主要由装配工序等待关联零部件齐套的时间产生。零部件子批完工后会进入半成品库存区,等待其关联任务都齐套后,才能由库存等待区转入到装配单元进行加工,在此等待关联零部件齐套的期间会产生相应的库存持有成本。本文借助分批生产与传输技术,将各层级的零部件划分为可以独立流转的子批。通过将子批在加工/装配资源上交叠并行生产,实现生产进度的协同。

图1 多层级装配作业车间简图Figure 1 Diagram of a multi-level assembly job shop
本文所考虑的多层级装配作业车间分批调度问题描述如下:在调度时刻,待交付的产品集合为P={Ph|h=1,2,···,p},对于任一类产品Ph,其需求批量为DBh,并具有特定的装配结构。产品Ph需要经过加工阶段与装配阶段,加工阶段共有a个加工单元M={Mi|i=1,2,···,a},而装配阶段有b个装配单元A={Ai|i=1,2,···,b}。零部件的加工/装配工艺路径因零件类型而异,面临的优化问题是对各类零部件进行批量划分,以确定零部件的分批数量以及子批的批量大小,再对分割好的各个子批进行优化排序,以最小化库存持有成本和拖期成本之和。
在构建多层级装配作业车间生产调度模型前,有以下假设:1) 在零时刻,所有零部件分割后的子批信息已知,并均可被选上机加工;2) 不考虑物料在资源之间的运输时间;3) 生产过程中没有物料短缺或者机器故障等异常扰动出现;4) 不同类零件子批之间在上机前的切换需要工序准备时间,同类零部件子批连续加工/装配不需要工序准备时间,工序准备时间只与工序相关而与子批的大小无关;5) 每个工件在任意一台机器上仅加工一道工序;6) 工序一旦开工,则不允许终止。
2 模型构建
2.1 模型相关符号定义
本文所涉及的符号与参数定义如表1所示。

表1 符号与参数定义Table 1 Definitions of symbols and parameters
2.2 数学模型构建
装配作业车间分批调度包括批量划分与子批调度两个决策,批量划分决策层一定程度上影响子批调度结果的优劣性。任务划分的子批过少,子批批量过大则不利于任务在车间流转,高负载车间环境下产品拖期风险随之增加;反之,任务划分的子批过多,虽然有助于加速任务交叠并行加工,但造成了因装夹工具切换而产生的准备时间增加,因部分子批提前完工而产生的装配齐套等待时间也随之增加。分批结果对因产品拖期而产生的惩罚成本与因装配齐套等待而产生的库存持有成本有深远影响,受到文献[15]所构建的数学模型启发,本节以最小化所有产品的库存成本与拖期成本之和为优化目标函数,构建了多层级装配作业车间分批调度模型,具体如下。
其中,式(1) 为本文的目标函数,即最小化所有产品的拖期成本与库存持有成本之和,通过统一量纲的方式将所有产品的拖期成本与库存持有成本累加。式 (2) 定义了待交付产品h的生产周期,其等于下属所有子批最晚完工时间;式 (3) 为基准交货期的设定,是以关键路径总工时与交货松弛系数之积;基于式 (3) 所生成的交货期基准,式(4) 与式(5) 分别表示交货期下界与上界;式 (6) 约束了工件子批Lhjs的加工顺序先后关系;式 (7) 则定义了工件子批Lhjs在紧前工序完工后,在紧后工序加工队列的排队等待时间约束;式 (8) 表示当且仅当工件子批的装夹类型与当前加工机器装夹类型一致时,不需要切换夹具等准备工作,否则需要额外切换夹具的准备时间;式 (9) 约束了装配工序的开工时间不得早于直属零部件的完工时间,并且装配子批的批量不得大于直属零部件的子批批量;式 (10) 表示产品h需求数量,下属零部件批量与各零部件子批量之间的关系;式 (11) 为工件批次Lhj的分批数量约束;式 (12) 表示所有零件的子批都可以在零时刻被选择上机;式 (13) 将拖期成本定义为产品h的拖期时间、需求数量、产品单位拖期成本之积,式(14) 将产品库存持有成本定义为产品h各层级零部件等待关联零部件完工所产生的装配等待时间、批量大小、单位库存成本之积;式 (15) 与式 (16) 则表示工件批次Lhj下的各个子批的加工/装配工时与准备工时是相同的。
3 算法设计
3.1 算法求解流程
多层级装配作业车间调度问题涉及批量划分与调度两个子问题,而处理该类问题的策略主要有分步优化策略和集成优化策略[15]。集成优化策略是将批量划分和排序两个子问题建立联合优化模型,并构建全局优化算法进行求解。集成优化策略可以确保求解质量,但过于低效的求解效率使其在实际生产中难以在可承受的时间内获取令用户满意的解。故本文采用分步优化策略,通过在计划层执行任务分批后,再对分割后的子批执行调度排序。以遗传算法为代表的智能算法具有良好的全局搜索能力,但子批调度问题涉及渐增性齐套约束,难以设计合适的基因编码表达方式以及高效的遗传迭代动作。启发式规则可以相对直观快速地反映多层级装配产品在生产过程所涉及的复杂装配约束。鉴于此,如流程图2所示,将遗传算法应用在批量划分问题上以迭代优化分批结果,再基于作业分派规则对生成的分批方案进行高效快速地调度排序,此类混合求解框架可以较大程度地发挥智能算法与作业分派规则的特点与优势。
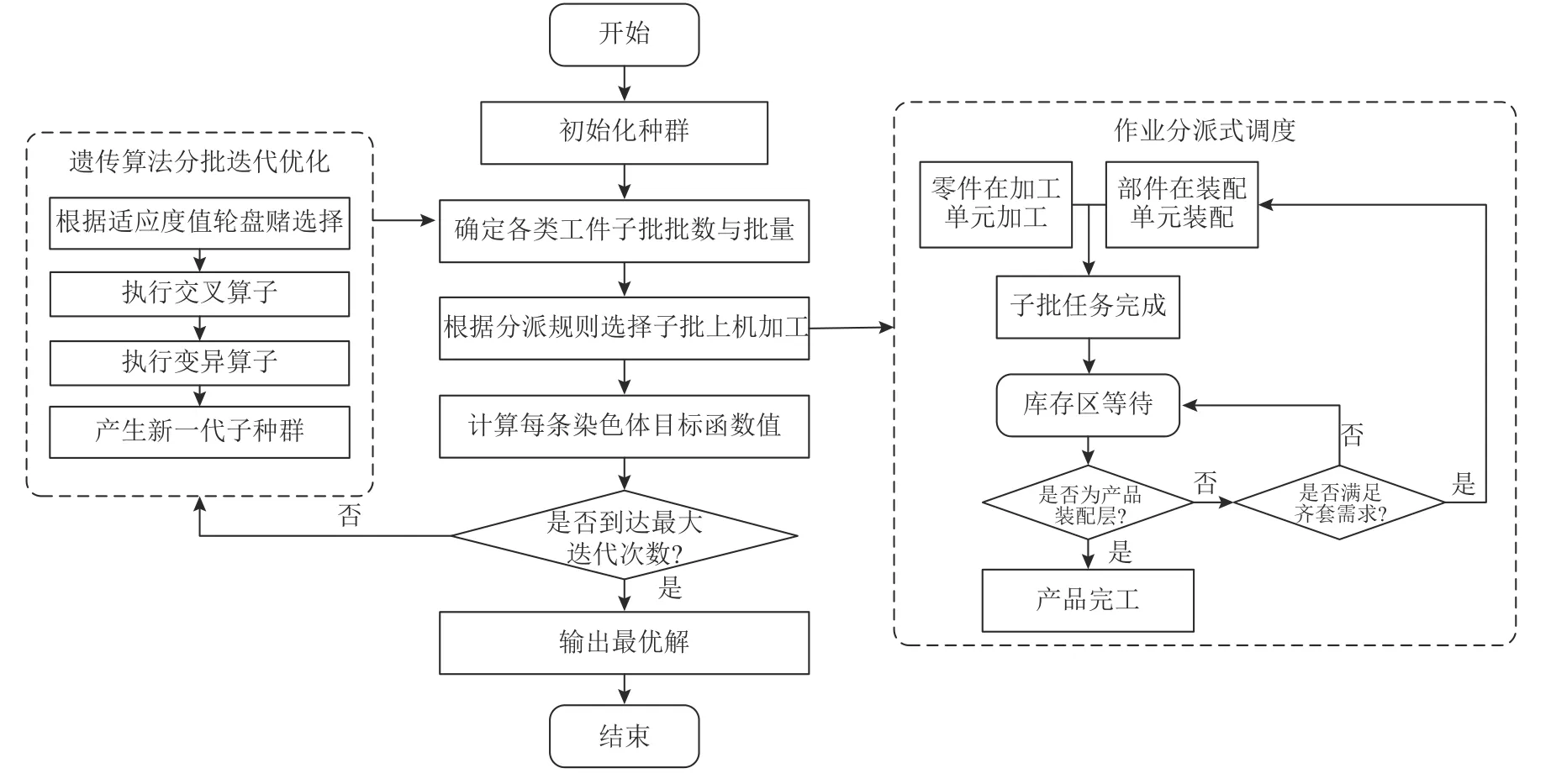
图2 混合求解算法框架流程Figure 2 Flow chart of the hybrid algorithms
3.2 遗传算法的分批优化
遗传算法 (genetic algorithm,GA) 是一个被公认为具有良好全局并行搜索能力的智能算法,其在作业车间调度等相关拓展问题的优化求解上被广泛应用。本文将遗传算法用于优化多层级装配作业车间的批量划分子问题,其涉及了各类工件需要拆分的子批数量以及各子批的批量大小。为此本节首先设计分批优化的染色体编码方式,为充分发挥遗传算法的全局搜索能力打下基础。其次,设计了一套交叉变异操作以维持生成子代解的合法性,并提升算法搜索效率。
3.2.1 染色体编码
本文设计了基于实数编码方式的二维数组式染色体,其中染色体结构的第1列表示的是各类工件被拆分成的子批数量,后续的各列依次表示被拆分后的各个子批的批量,所以一行基因代表了某一类零部件的分批结果。如图3所示,一个待交付数量为10的单装配层级产品,其直属的4类加工件和一类装配件需求数量也为10。图3所生成分批方案构成了一个5×5维度的数组,各类工件的分批批数依次为5、2、4、3、2。值得注意的是,当分批后的子批数量不满足染色体的最大有效长度 (产品下属各类工件的最大分批数量),长度不满足的部分需要用零进行补充,如图3中第2行的工件被分为2个批量为5的子批。
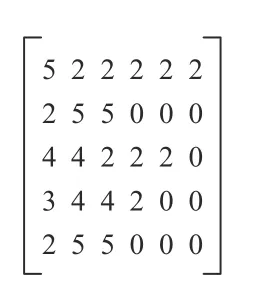
图3 染色体编码结构示例Figure 3 An example of chromosome coding
3.2.2 交叉与变异操作
为了保证编码在遗传迭代过程中的完整性,设计了一套面向装配作业车间分批问题的交叉和变异操作。如图4所示,对于需求数量为10的单装配层级产品,父代1与父代2两条染色体结构表征其分批的两套方案。先对父代1与父代2执行交叉操作,将两条父代染色体中的第5类装配件的编码信息进行交叉互换后,生成两个子代染色体。
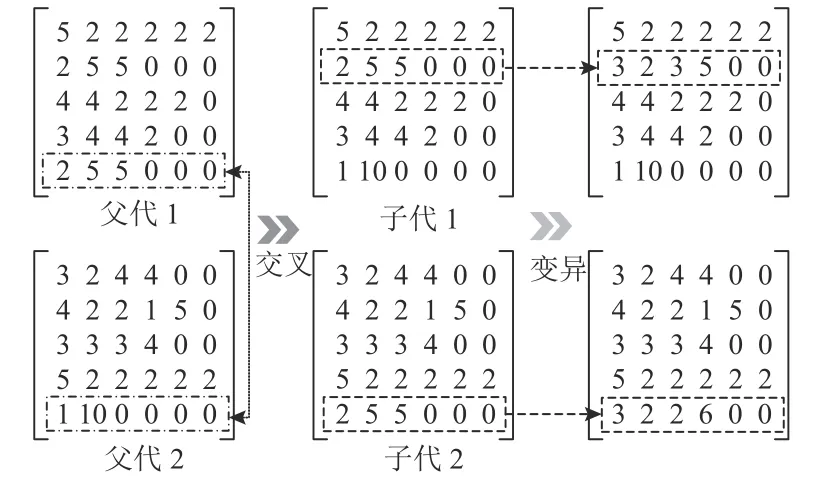
图4 染色体交叉变异操作示例Figure 4 An example of crossover and mutation operation
基于交叉操作阶段生成的两个子代染色体,分别对子代1的第2类工件与子代2的第5类工件执行变异操作。变异操作作用于染色体编码第1列的分批信息,将子代1的第2类工件与子代2的第5类工件分批数量都从2变为3以后,随即产生的子批批量也重新生成。交叉变异操作执行完成后,再根据轮盘赌的方法,基于种群的适应度函数进行选择操作。
3.3 作业分派式调度
基于遗传算法所确定的工件分批方案,采用基于优先度的作业分派规则对划分的子批任务进行调度,总体流程如图2所示,详细步骤如下。
步骤1待交付产品下属的所有任务分为3个集合,待完工任务集合对应的是各台加工/装配单元中的等待队列任务集合,表示子批任务还有未完成的加工/装配工序;装配等待任务集合对应的是零部件已经完成所有工序,但需要等待关联任务完工齐套后以执行更高层级的装配;可交付队列则表示产品已经完成总装可以交付用户。
步骤2根据相应的作业分派规则,依次安排待完工任务集合的子批任务执行加工/装配任务。
步骤3若子批任务完成当前加工/装配工序后仍未完工,则继续执行步骤2。如果子批任务完成了加工/装配阶段的所有工序,则将其状态转为完工并转入装配等待任务集合并执行步骤4。
步骤4判断子批任务所处的装配层级,如果子批任务未到达最高装配层级,则执行步骤5;若子批任务已经达到产品总装层,则将子批任务转移到可交付队列。
步骤5判断子批任务同属装配层级的其他关联任务是否已经齐套,且各类关联工件子批的最小批量是否满足上一层及装配子批的批量开工需求,若满足则将子批任务转入待完工任务集合,否则保留在装配等待队列中等待关联任务完工。
多层级装配作业车间调度中协同关联批次加工进度存在两个难点:1) 差异化的工艺路径长度以及工序工时使得部件直属零件的进度难以协同;2) 部件下属关联零部件的最小完工批量要满足其装配工序的批量开工需求。鉴于此,高效的作业分派规则可以快速地基于分批结果生成调度方案。根据装配作业车间调度相关文献[6],已有的装配作业调度规则通常按以下4个典型维度进行设计。
1) 流水时间类的规则:与加工任务工序工时,任务工艺路径累计工时等参数相关;
2) 订单层协同的规则:与订单下属各任务的加工进度相关;
3) 任务层协同规则:与任务下属未完工工序、工时等参数相关;
4) 交货期设置规则:与订单、工序交货期等参数相关。
表2为相关文献所涉及的装配作业车间分派规则。
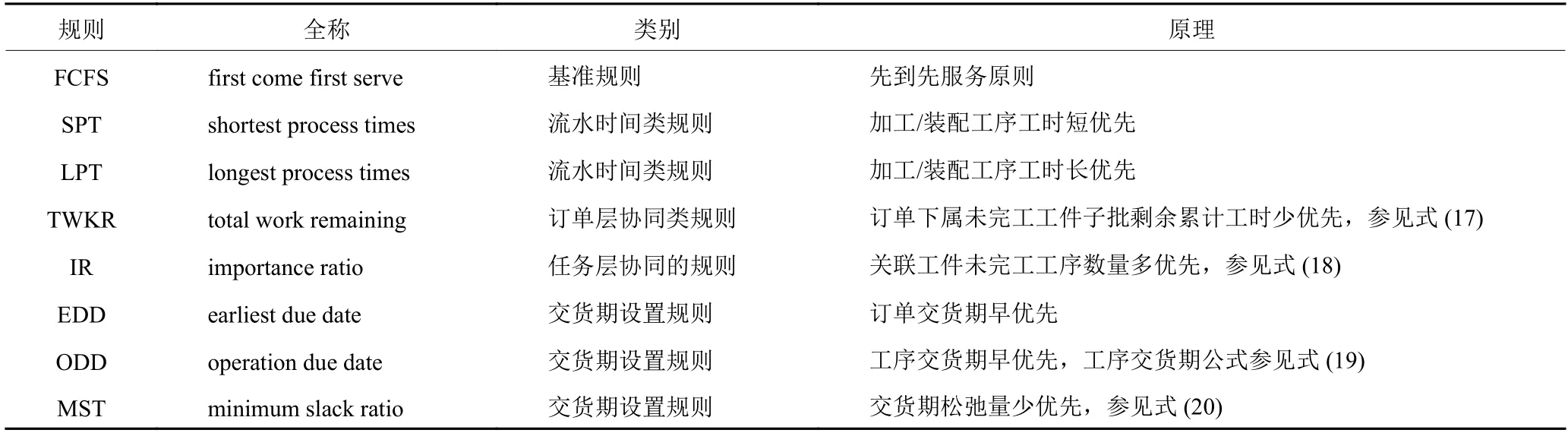
表2 装配作业车间作业分派规则Table 2 Priority dispatching rules in assembly job shops
其中,RANKhjsk为子批任务的加工优先级;UTh为Ph工件类型 数;UShj为Lhj未完工子批数;UOhjs为Lhjs未完工工序数;RM为未完工子批任务。
4 仿真实验
4.1 仿真参数与实验设计
装配作业车间的产品BOM结构特征与其装配层级数量、各层级的直属零部件数量紧密相关,分批调度对差异化产品产生的协同性能也会有所不同。文献[16]考虑了3种特点鲜明装配结构的产品。1) Flat型产品。是由多个零件直接装配而成的单层级树形结构,仅仅需满足全局性装配齐套,见图5 (a)。2) Tall型产品。属于多层级树形结构,每一层级仅有两个直属零部件装配而成,属于渐增性齐套,见图5 (b)。3) Complex型产品。综合了前两种类型产品的特征,既属于多层级树状结构,每层级的直属零部件也不少于两个,见图5 (c)。本文的实验目的之一就在探究所提出的分批调度算法在图5所示9种产品结构上的性能差异。
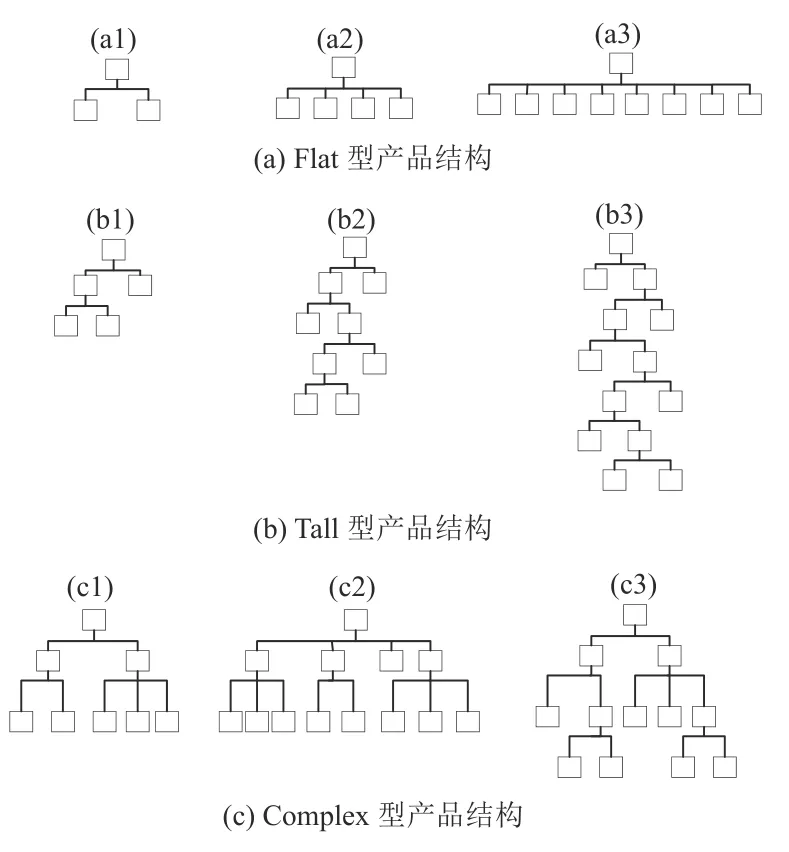
图5 产品树状结构Figure 5 Tree structures of assembly products
分批策略决定了批量划分问题的解空间,是影响分批调度算法性能的重要因素。常用的分批策略有等量分批,一致分批与可变分批[9]。其中,等量分批因为其直观、计算效率高的特点被应用在批量流相关研究中[17]。与此同时,等量分批也被认作是可变分批的一种特殊形式,本文的实验目的之二就在于研究可变分批策略相比等量分批策略是否可以提高混合算法的调度性能。
本文所考虑的优化目标与交货期设置紧密相关,装配作业车间的交货期设置通常是参照经典的关键路径法,其中涉及交货期强度系数。本文将探究在不同交货期强度下,评估分批调度算法在各类装配树形结构产品下的性能变化,并以此为设定交货期强度基准。
按照前文所述的实验动机,本文的仿真实验将如下推进:首先,在不同交货期强度下,分析所提出分批优化调度算法在各类产品下的性能变化,并设定交货期基准;其次,在给定的交货期设置下,分析不同作业分派规则在不分批策略 (none sublot,NS) 对各类树形结构产品的性能影响;最后,分析比较等量分批 (equal sublot,ES) 与可变分批 (variable sublot,VS) 两种策略与作业分派规则在各类树形结构产品下的耦合性能。
如表3所示的仿真实验所涉及参数是基于文献[15]而来,为避免实验中存在过多自变量,本文将所考虑的9种树形结构产品按照其结构特征分为Flat、Tall、Complex 3类依次进行调度。
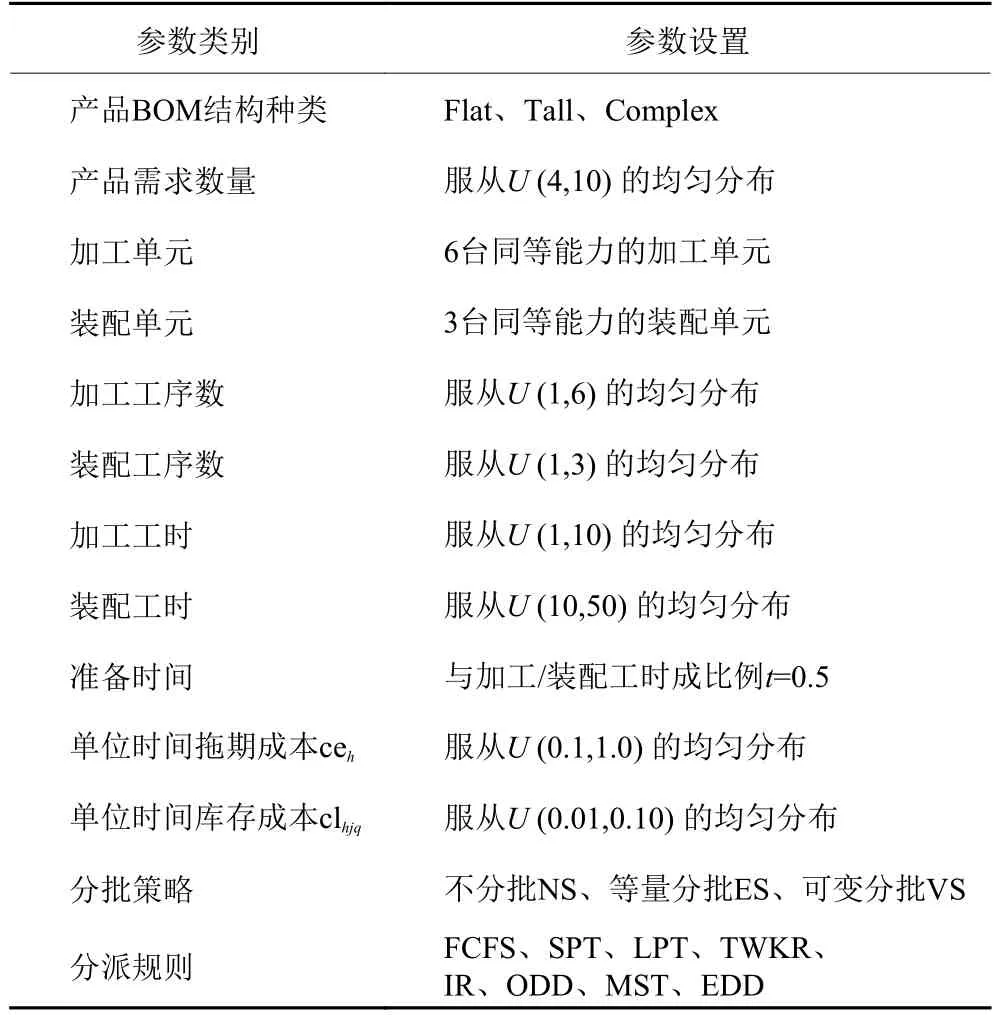
表3 实验参数设置Table 3 Parameter settings of experiments
4.2 实验结果与分析
本文所构建的多层级装配作业车间实验平台基于Matlab2016b开发,在同一种实验参数组合下取10次实验观察值的均值作为最终的实验结果。为确保遗传算法的收敛性与稳定性,本文首先开展一系列预实验以确定遗传算法相关的重要参数:种群大小为100条染色体,迭代终止条件为最大遗传代数100代,交叉概率为0.7,变异概率为0.05,代沟设置为0.9。为更好地分析分批调度算法在不同实验参数下的性能变化,除去优化目标Obj以外,还统计了拖期总成本CE、库存总持有成本CL和所有产品完工后的最大完成时间Ctmax作为观察指标。
4.2.1 算法性能受交货期强度设置的影响
本文所考虑的实验变量因素较多,出于交货期设置对优化目标有较大影响考虑,第一阶段的实验先在3种分批策略以及各类树形产品结构下,分析算法性能受交货期强度设置的影响。混合算法中采用ODD规则以控制变量,通过预实验,交货期松弛系数λ值1.15、1.35、1.55分别代表3种交货期强度(紧、中、松)。
图6表现了3种策略下算法的优化目标受到交货期设置而产生的性能变化。如图6 (a) 所示,在NS策略下,算法在Tall型结构的产品调度结果最差,Complex其次,Flat型最好。在同等交货期强度下,Tall型产品的结构特征是装配层级较多,这不仅容易造成相对高的产品拖期风险,更会产生因渐增性齐套装配带来的库存持有成本增长。随着交货期强度逐渐变低,目标函数会出现拐点,原因在于高交付压力下容易产生高额的拖期惩罚成本,而低交付压力则又容易因交付时间未到而产生额外的库存持有成本。由此可见,交货期强度的合理设置对优化目标的影响。
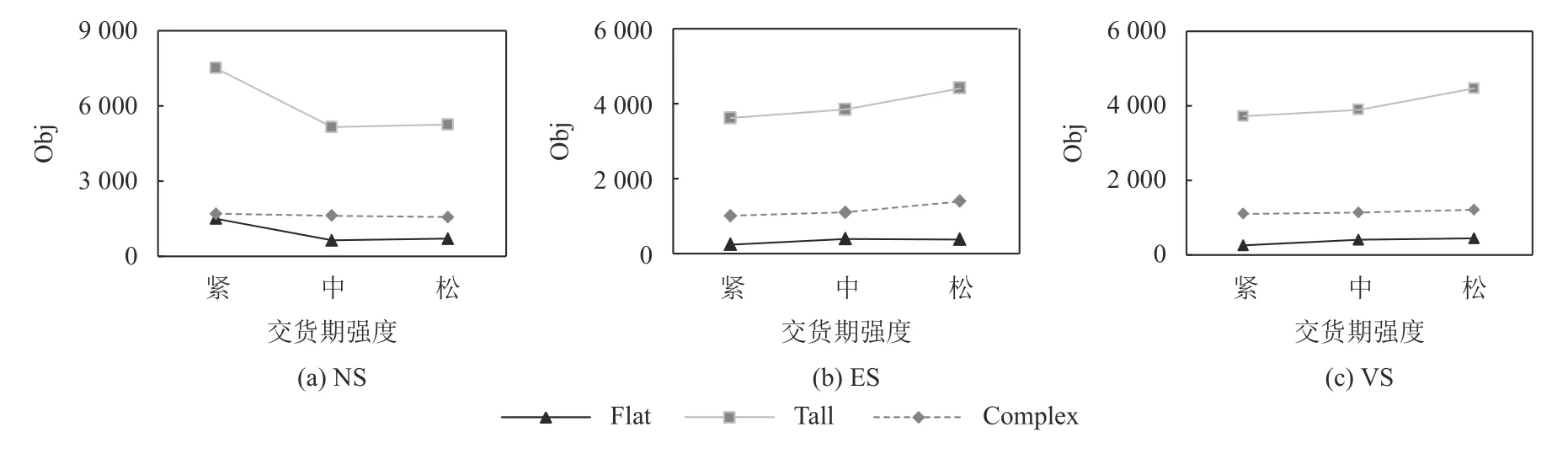
图6 交货期强度设置对算法的影响Figure 6 The influences of delively time intensiry on algorithms
图6 (b) 和 (c) 分别为等量分批与可变分批策略下目标函数随交货期变化,可以明显发现3类产品结构在同等交货期强度下,分批策略对优化目标有不同程度的性能提升。不同之处在于,优化目标是随着交货期强度下降而劣化,这一方面说明了相比低交货期强度带来的低拖期惩罚,分批策略下可能会造成更多因装配等待而产生的库存持有成本。另一方面,过宽的交货期强度也使得过早完工的产品无法交付而产生额外的库存持有成本。
4.2.2 不分批策略下调度规则的性能分析
根据前一阶段的交货期设置的实验结果,本节将进一步分析作业分派规则的选择对混合算法的性能影响。为控制变量以及屏蔽过多实验因素干扰,本阶段采用NS策略,交货期系数λ设置为1.35。因为NS策略下,前阶段实验结果显示该交货期设置可以获取优化目标的临界点。
本阶段将对8种作业分派规则下的混合算法,在3种装配结构下分析其优化目标、拖期成本、库存持有成本以及Ctmax等多个指标。实验结果如表4~表6所示,可以得出以下3个初步结论。
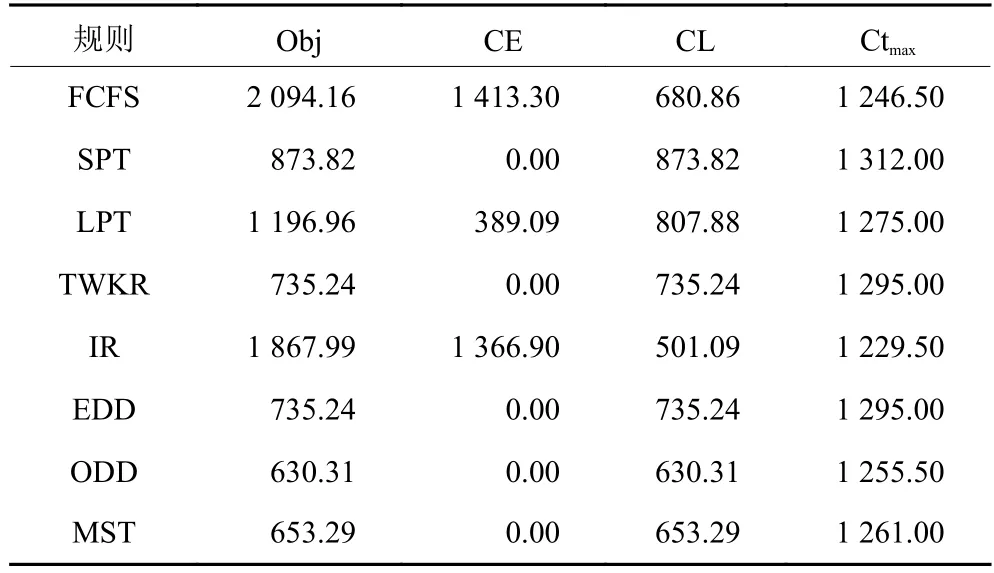
表4 Flat型产品在NS策略下的调度结果Table 4 Scheduling results of flat structure products under NS strategy
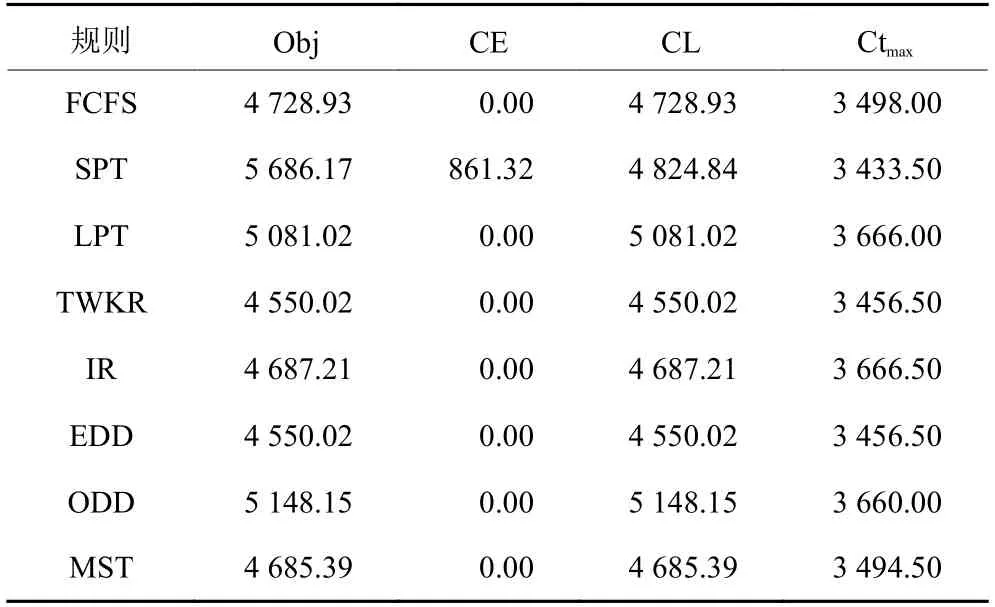
表5 Tall型产品在NS策略下的调度结果Table 5 Scheduling results of tall structure products under NS strategy
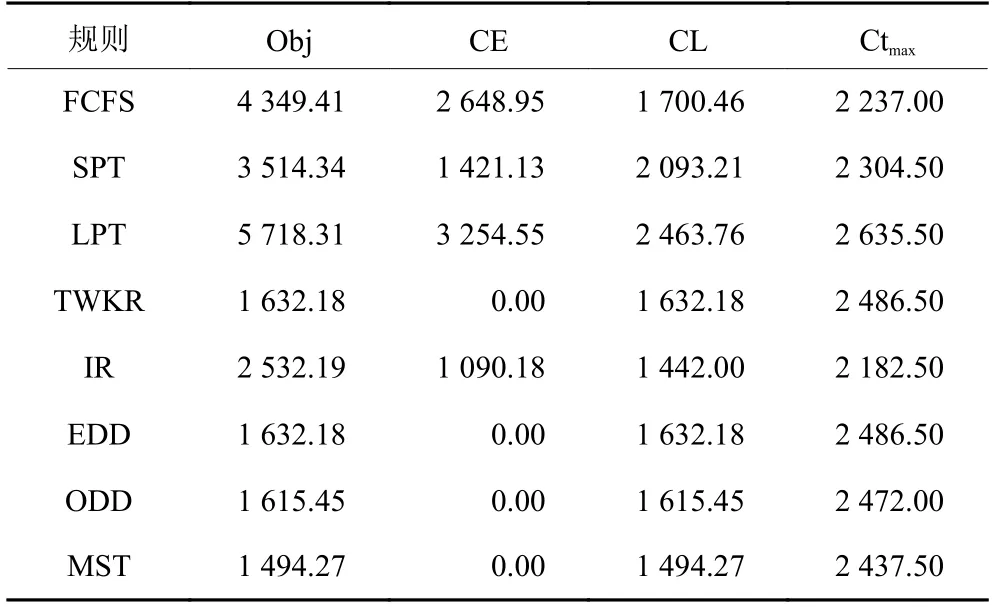
表6 Complex型产品在NS策略下的调度结果Table 6 Scheduling results of complex structure products under NS strategy
1) 基于交货期属性的作业分派规则 (EDD、ODD、MST) 在各类产品结构下都表现出了较好的性能,在Flat与Complex型产品下,交货期类的规则优势非常明显。
2) Flat型产品下,ODD规则性能最优,原因在于Flat型产品属于全局性齐套,面向工序交货期的规则可以有效引导关联零部件在单层装配结构下的进度协同性;而Tall型产品结构下EDD规则的性能好于ODD规则,因为交货期设置考虑了装配工序、装配层级数等因素,产品的交货期差异比较明显。EDD规则可以有效协同某一产品下属所有零部件的关联任务进度,因其赋予下属零部件相同优先级;最后在Complex型产品下,MST规则通过协调交货期与总工时之间的进度来设置不同程度的优先级,从而保证良好的进度协同性。
3) 在3种树形结构的产品调度中,TWKR规则都取得了EDD规则相同的性能,因为这两种规则都是面向订单层的,其决定了下属的所有关联零部件加工优先级都一致,另外交货期设置也跟累计加工与装配工时相关,所以获得相同的调度性能也符合预期。
4.2.3 分批策略下作业分派规则适应性分析
前一组实验初步分析了NS策略下不同分派规则的调度性能,接下来要对作业分派规则在等量分批策略与可变分批策略下的性能进行产品结构的适应性分析,图7为3种树形结构下作业分派规则与两种分批策略的耦合调度性能比较。
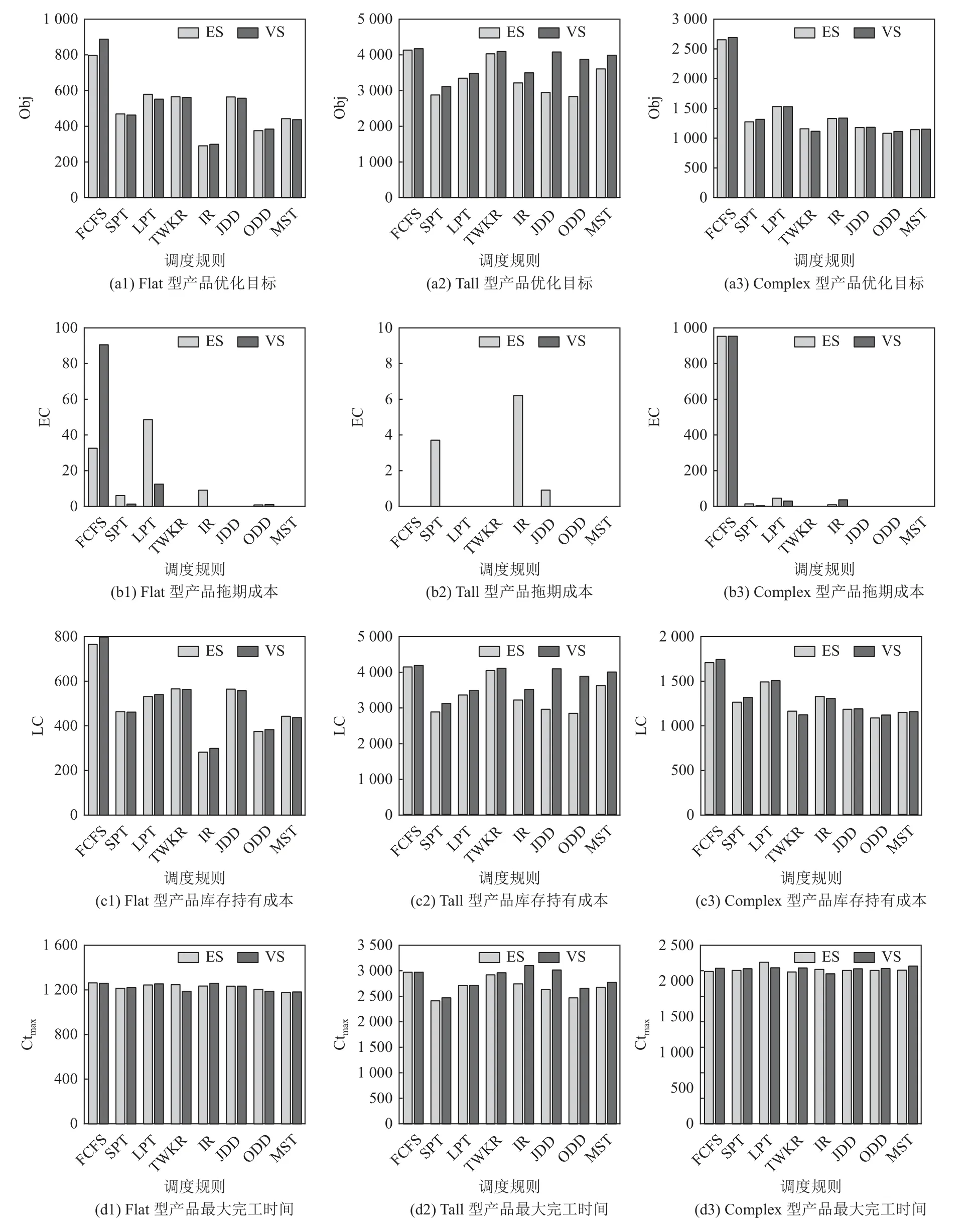
图7 分批策略与调度规则在不同树形结构产品下的耦合性能比较Figure 7 Comparison of coupling performance between lot-splitting strategies and priority dispatching rules under different tree-structure products
对各组实验结果进行初步分析可以得到如下结论。
1) 分批策略下,各个作业分派规则的性能相比NS策略都有显著提升。在分批策略的选择上,ES策略在绝大多数的场景下都好过VS策略,原因在于ES策略产生的子批数量以及批量大小更加均衡,一定程度上可以促进关联任务之间的进度协同性。例如在图7 (c2)中,在Tall型产品下ES策略的库存持有成本要明显优于VS策略。虽然ES策略的分批结果理论上是VS策略分批结果的子集,但在限定的迭代优化条件下,VS策略仅能在部分场景中达到ES策略的分批效果,故而会出现两种分批策略性能差异不大的现象。
2) 在ES与VS策略下,基于交货期的作业分派规则ODD、EDD、MST在3种产品的优化目标上都有良好的调度性能。这延续了NS策略下的作业分派规则性能特征,一定程度上说明了作业分派规则的效力在分批策略下得到了良好的继承。
3) 如图7 (a1) 所示,在Flat型的产品下,基于ES分批策略的IR规则在目标函数值上表现最佳。因为Flat型产品属于全局性齐套,下属任务的协同性更多取决于关联任务未完工的工序数量差异。在等量分批策略下,IR规则可以很好地处理关联任务的加工进度协同。如图7 (a2) 所示,在Tall型产品下,基于ES策略的SPT规则可以获得最佳的目标函数值。Tall型产品因为涉及的装配层级较多,而每一层级的直属装配件类型较少。SPT规则可以加速批量较小的子批任务的流转,进而减少装配等待时间,所以库存持有成本有很大改善。如图7 (a3) 所示,在Complex型产品中,基于ES策略的ODD规则在目标函数值上表现最佳。Complex型产品具有较多的装配层级且每一层级的直属装配件也较多,加之零部件具有差异化的加工/装配工序与工时,ODD规则基于订单交货期生成零部件在加工/装配阶段的工序交货期,可以作为各层级关联零部件生产/装配进度协同的基准有效降低库存持有成本 (见图7 (c3)),进而取得更佳的目标函数值。
5 结语
本文以多层级装配作业车间分批调度问题作为研究背景,构建了以最小化拖期成本与库存持有成本之和为目标的调度模型,提出了基于遗传算法与作业分派规则的混合求解算法,利用遗传算法出色的全局搜索能力保证分批问题的求解优度,再利用作业分派规则对分批结果快速生成调度计划。鉴于交货期、分批策略以及作业分派的选择对混合求解算法存在一定的影响,设计了渐进型的仿真实验进行评估分析。实验结果表明,1) 给定交货期强度下,产品装配层级越多,产生的装配齐套等待时间越长,进而导致库存持有成本剧增,分批调度算法在目标函数上呈明显劣化趋势。2) 分批调度可以使批量小的子批任务有较好的流动性,促进各层级关联零部件的加工协同,降低装配齐套等待产生的库存持有成本。3) 在给定迭代优化条件下,等量分批策略可以有效降低库存持有成本,故而可以获得比可变分批策略更为可观的优化目标值。4) 分批调度的混合求解算法需要考虑产品的结构特征,进而选择合适的作业分派规则。
针对本文所考虑因素的不足,未来将从以下两个方面进行研究:1) 建立更为全面的制造成本计算体系,将在制品成本、准备时间成本和转运成本考虑到优化目标,从而使模型更为贴合实际;2) 将子批传输策略引入分批调度模型,进而对生产的流动性进一步改善。

