可移动货架下的储位选择与拣货路径联合优化

赖品谚，张大力，赵思翔

(上海交通大学 1.深圳研究院，广东 深圳 518057；2.中美物流研究院，上海 200030)

近年来，随着B2C电商零售的快速发展以及网络直播带货的流行，客户在线订单逐渐呈现小批量、多品种、异质化的趋势，这对仓库内作业的时效性提出了更高的要求，如何实现快速拣货已成为现阶段物流仓储公司面临的最重要挑战之一。为了提高订单分拣效率，文献[1]中提出重要仓储决策问题包括仓库布局设计、存储位置分配、订单批处理以及拣选路线规划，而更合理的存储库存单元(stock keeping unit,SKU) 是提高订单拣选效率的有效方法[2]。传统仓库储位采用SKU一对一存储，而当需要在短时间内挑选大量不同种类的商品时，Weidinger[3]提出一种针对在线零售商需求的分散存储策略，将同一种SKU分散存储到仓库各个位置的储位中，增加拣选路径柔性，能够有效缩短到任意SKU的平均距离，这种策略带来的问题是如何在多个储位中选择最优的拣选储位。在此基础上，可移动货架仓储系统的出现给拣货效率的提高带来新的希望[4]。王征等[5]阐述了可移动仓储系统的使用原理，其货架体型较小可被移动到仓库任何位置。移动式货架的出现使得仓库布局可以实时调整，增加了储位管理的灵活性，同时也将储位优化问题提到了一个新的高度。如何对货架进行移动且何时对货架进行移动都是亟需研究的问题，每次的货架移动都会直接影响存放的SKU之间的距离，不仅需要考虑移动后新的货架布局给订单拣货带来的移动距离的减少，还需要考虑移动货架时产生的移动成本。

针对分散存储中储位选择与拣货路径的问题研究，Yang等[2]提出一个订单批量优化算法包，具体解决储位选择、路径规划和订单分批3个问题，对于储位选择和订单分批提出多种启发式算法。此后Weidinger[3]研究矩形分散仓库的拣货路径问题，提出联合混合整数优化模型，并证明了其NP-hard性质，通过3个启发式的优先规则来完成对储位的选择问题。而基于一些储位选择的标准，Dmytrów[6]使用广义距离度量创建一个混合变量，对所有储位进行排序，并对排名高的储位进行选择。目前对于拣货储位的选择多是基于规则的选择方法，很少有将其与拣货路径联合起来进行建模求解。针对可移动货架的研究，王征[5]等基于顾客订单建立了货架热度和关联度生成模型，建立考虑机器人重载和空载行驶距离最小化的双目标整数规划模型，并设计了禁忌搜索启发式求解算法。Li等[7]解决了货到人拣选模式的最佳移动货位选择问题，目标是最小化完成所有订单中移动货架的总行程距离，建立整数规划模型，提出一种具有多项式复杂度的三阶段混合启发式算法。Xiang等[8]研究可移动系统中的储位分配和订单批处理问题，通过储位分配以最大化同一货架中产品的相似度，对于订单批处理问题，提出一种启发式方法来生成初始解决方案以及可变邻域搜索启发式方法对解进行改进，以最小化访问货架的次数。Valle等[9]研究同时将订单和移动存储架分配给静态拣货员的问题，同时还考虑如何对货架进行排序，并提出两种启发式方法。目前的货架移动研究都基于“货到人”模式下通过机器人对货架进行移动，而“人到货”模式下也存在通过移动货架来加快拣货效率的需求，许多该模式仓库的经理担心自动拣货系统的高投资成本[10]，所以这部分的问题研究仍有所空缺。

因此，本文针对“人到货”拣货模式和分散存储策略，研究可移动仓储系统中的订单拣货路径优化问题，提出一个包含储位选择联合路径规划优化模型和货架移动优化模型的双层优化模型，并设计相应的启发式算法对其进行求解，最后进行数值实验对算法的有效性进行验证，实现了单日订单拣货量和拣货效率的提高，以及整体仓储和拣货成本的降低。

1 模型构建

考虑某仓库的存储策略为分散存储，一种SKU可存放在仓库多个储位中，但一个储位只能存放一种SKU，在对拣货路径进行优化的同时需要对储位选择进行优化，其中存储单位为储位和货架，储位是最小的存储单元。考虑可移动式货架，其中货架是多个储位的集合且有着不同的长度，货架的长度等于包含的储位数量，一个货架只能存放一种SKU。货架具有可移动的属性，但货架中的储位不可拆分，移送时需对货架整体进行移动，而货架的可移动性也会导致仓库从传统的固定式布局转变为可变式。拣货通道可以是传统平行通道，也可以是交错间隔的通道。一些流行的路由启发式算法只能应用于单块和多块传统矩形仓库，对于3块或更多块的非传统矩形仓库并没有最优算法[11]。货架与储位的关系如图1所示 (数字代表SKU的编号)。本文考虑使用储位间的距离矩阵来表示仓库的货架布局，同时使用储位间的距离来表示拣货时的移动时间成本。而需要解决的问题是，针对一批待拣订单，如何移动货架更改SKU的存储布局，使得拣货路径总和最短。

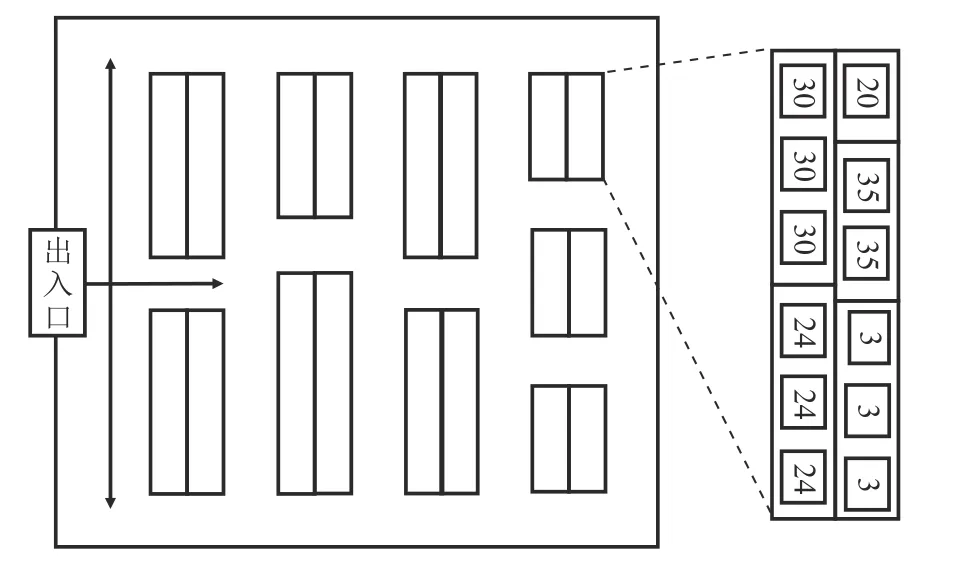
图1 仓库中的布局与货架Figure 1 Layout and shelves in a warehouse

本文针对性地构建一类双层优化模型，双层规划就是对两个决策模型之间的决策层次和交互进行分层，上层通过考虑下层的最优解来优化受约束的上层目标函数[12]。在上层货架移动模型中优化SKU存放的储位集合，获得未来拣选时的仓库布局，而下层拣货路径模型旨在优化此布局下的订单拣选路径长度总和。不难看出，上层的求解结果将会影响下层模型的距离矩阵，影响各SKU之间的拣选距离，从而影响下层模型的目标函数；同时可以用下层优化模型的最优目标值来衡量上层模型的优化效果，以便上层模型迭代寻优。上层优化结果中设定移动单元为货架，而不同类型的货架具有不同的长度，且一个货架可存放多个相同SKU的储位，例如图1中SKU30存放在长度为3的货架中，SKU35存放在长度为2的货架中。模型中考虑长度相同的货架可以进行位置交换。下层优化结果中设定拣货单元为储位，根据现有的订单需求和当前储位布局，对SKU的拣货顺序和储位选择进行决策，即对于任意一个存放在多个储位上的SKU选择一个最优的拣选储位，以完成订单需求的拣货任务。

1.1 上层优化模型：货架移动模型

该模型对货架进行移动或交换，进而改变仓库的SKU布局，使得拣选者能够以更短的路径完成订单需求任务的拣选。对该问题作出如下假设：1) 只能够交换长度相同的货架；2) 货架移动后不能改变拣货通道的位置；3) 货架移动过程的时间可忽略。本文模型中的符号定义如表1所示。

表1 模型符号定义Table 1 Symbol definitions in the model

其中，使用 θ 定义为 θms的简写来表示上层 模型输出的移动储位后仓库的SKU布局，D(θ)为该布局θ下的最短拣货路径，且由下层模型求解得出。上层模型如式(1)～ (7)所示。

目标函数 (1) 表示优化问题的目标为拣选此批订单所需的拣选路径长度和货架移动成本之和最小；约束 (2) 为交换平衡约束，即货架m跟n交换等同于货架n跟m交换；约束 (3) 为交换长度约束，保证交换的货架长度相等；约束 (4) 为交换数量约束，对于任意一个货架最多只能与其他货架交换一次位置；约束 (5) 为交换布局约束，记录移动货架后的SKU存储布局。

1.2 下层优化模型：拣货路径模型

该模型对需求SKU的存储储位进行选择并规划拣货顺序，使得总拣选路程距离最短。此处作出如下假设：1) 不考虑补货策略，假设在拣选过程中库存充足；2) 不考虑拣货容器的容量限制，因此只需考虑SKU需求的种类，不考虑需求的数量；3) 分配的订单中所有SKU需要在一次拣货作业中完成拣选。下层模型如式(8)～ (15)所示，模型中的符号定义见表1。

其中，目标函数 (8) 为最小化拣货路径总长度；约束 (9) 和 (10) 为出入口约束，拣货员从仓库出入口出发最后回到出入口；约束 (11) 为平衡流约束，保证对于任意储位进出相同；约束 (12) 为需求约束，满足需求SKU的拣货任务；约束 (13) 为消除子回路约束。

2 算法设计

针对双层优化模型本文提出一种双层的元启发式算法框架，将自适应大邻域搜索算法 (adaptive large neighborhood search,ALNS) 和遗传算法 (genetic algorithm,GA) 相结合进行求解。

2.1 算法框架

下层的拣货路径优化模型中采用遗传算法对储位的选择以及拣货的顺序进行求解，其求解结果为某一仓库布局下的订单需求的最优拣货路径；上层模型中采用搜索能力较强的自适应大邻域搜索算法求解。此外本算法使用Apriori关联算法作为ALNS的初始解加快算法收敛，双层元启发式算法框架如图2所示，上层ALNS算法每求解出一个储位布局的邻域结果便传递到下层GA算法中，下层GA算法计算该邻域结果上的所有订单需求的最优拣货路径距离和，上层ALNS算法通过下层GA算法的返回值在不同的邻域中进行搜索对比，通过若干次迭代，最终选出最优的邻域结果作为货架移动后的仓库储位布局。双层元启发式算法框架具体包括3个算法模块，分别为Apriori、GA和ALNS，具体算法框架的流程图如图3所示。

图2 双层元启发式算法框架Figure 2 Framework of the bi-level meta-heuristic algorithm

图3 双层元启发式算法流程图Figure 3 Flowchart of the bi-level meta-heuristic algorithm

2.2 算法描述

初始化环节，Apriori算法通过计算数据的支持度和置信度来度量数据间的关联性，Agrawa等[13]首次提出Apriori算法并用于大型数据库的商品关联规则挖掘。Wu[14]基于Apriori算法研究智能电商物流中心订单中不同商品之间的相关性，只有支持度与置信度同时达到了最小支持度与最小置信度，此关联规则才会被称为强关联规则。Apriori算法把满足最小支持度的集合定义为频繁项集，通过逐层迭代的方法，先找出频繁项集F1，再利用F1找出频繁项集F2，直到找出所有的强关联性集合。基于强关联性结果，根据其关联性强弱按顺序可以对货架进行交换，使得具有强关联性的SKU货架尽可能接近，以减少拣货路径距离。本文将根据Apriori的关联结果对货架进行移动作为后续ALNS算法的初始解，移动方法步骤如下。

1) 定义最小支持度和最小置信度并得到强关联性SKU集合，将集合按照关联强度排序。

2) 按顺序选择相应的强关联SKU并进入步骤3)，如果已完成对所有强关联组合的移动则进入步骤5)。

3) 找出该强关联组合中k个SKU距离仓库出入口最近的货架M1,···,Mk，令固定货架FM=min(,···,)，其中为货架Mk距出入口0的距离，移动货架集合SM=MFM。

4) 令dFM为固定货架到其他所有货架的距离列表并按升序排序，依次选择dFM作为被移动货架，若符合条件(1)～ (3)则将被移动货架与移动货架进行交换。

(1) 被移动货架从未被交换过。

(2) 被移动货架和移动货架的长度相同。

(3) 被移动货架距离固定货架的距离小于移动货架距离固定货架的距离；直到所有移动货架完成交换返回步骤2)。

5) 所有货架移动后的结果作为ALNS算法的初始解。在得到ALNS算法的初始解后，通过GA算法计算该初始解在需求订单下的拣货路径长度，并作为判断SKU储位布局好坏的标准，即拣货路径长度越短，表明在该布局下能够更快地完成对订单的拣货工作。由于本文仓库的存储策略为分散存储，即一种SKU可以存放在多个货架中，因此在GA算法的染色体编码设计中不仅需要考虑拣选SKU的顺序，还同时需要考虑选择SKU对应哪一个货架中的储位。染色体编码如图4所示，每个SKU片段携带一个储位片段构成一次拣选片段。GA算法的流程包括二元锦标赛选择、交叉和变异操作。染色体交叉和变异过程如图5所示，随机对不同染色体的交叉使得产生不同顺序以及不同选择储位的解，对染色体进行变异则随机交换两个SKU并随机更改其选择的储位。到达迭代上限后，GA算法输出该储位布局下的拣货总距离。

图4 GA算法染色体编码Figure 4 Chromosome coding of GA

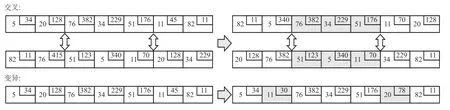
图5 GA算法交叉和变异Figure 5 Cross and mutation of GA

ALNS算法采用内层与外层的迭代方式对邻域进行搜索，内层结合模拟退火的思想，通过降温的方式进行搜索，外层限定终止条件，即达到最大迭代次数，不满足终止条件就进入内层继续搜索。ALNS算法的核心思想是通过不断地破坏和修复解从而完成对解空间邻域的搜索，并自适应地调整破坏算子和修复算子的权重，通过该权重控制每个修复算子和破坏算子在搜索期间使用的频率，表现更好的算子将获得更高的权重，从而提高算法的搜索寻优能力。本文基于Apriori算法结果的基础上，使用ALNS算法进一步对货架移动问题进行优化。在算法中共定义了两个破坏算子 (随机破坏和贪婪破坏) 和两个修复算子 (随机修复和贪婪修复)，随机破坏指随机选择多个货架并移除；随机修复将移除的货架随机插入至空闲位置；贪婪破坏指通过轮盘赌的方法选择多个需求SKU的货架并移除，需求中出现的次数越多轮盘赌选中的概率越大；贪婪修复指将移除的货架中SKU需求数量多的优先插入靠近出入口的空闲位置。

ALNS算法在解的接受准则上，为了避免只接受最优解而陷入局部最优，使用模拟退火准则在一定概率下接受劣解，该概率P(dE)=exp(dE/T)，其中 dE表示当前解与最优解之差为负值。ALNS算法在迭代时根据算子的权重使用轮盘赌的方式选择算子，通过选择的破坏算子和修复算子生成新的邻域解，并通过式 (16) 动态调整破坏算子和修复算子的权重。

其中，ρo为算子权重，uo为算子使用次数，so为算子分数，b为权重更新系数。算子分数由算子的表现情况阶梯式给分，得分越高表明算子表现越好。算子分数的增加分为以下4种情况：1) 新解为全局最优解，so+1.5；2) 该解不是全局最优解，但优于局部最优解，so+1.2；3) 模拟退火准则接受该劣解，so+0.8；4) 拒绝该劣解，so+0.6。在本文中，因为邻域搜索的规模较大，若如图3所示流程中每搜索一个邻域解调用一次GA算法求解拣货路径，则会消耗大量的时间。因此为了加速ALNS算法的求解过程，考虑在对邻域解调用GA算法前先计算其贪婪初始解Dg，贪婪初始解每次寻找离当前最近的储位。如图6所示，其中θ 为当前解，θ′为内层迭代的局部最优解，θ∗为外层的全局最优解 (文中所指的外层全局最优解表示遗传算法在指定精度或迭代次数下得到的算法最优解)。若Dg(θ)＜Dg(θ′)，则认为 θ可能为优解，并调用GA算法求解其拣货路径长度D(θ)，否则采取模拟退火的接受准则。若接受则同样使用GA算法求解拣货路径长度，否则定义为劣解。在求解出当前解θ 的拣货路径长度D(θ)后，与局部最优解的拣货路径长度D(θ′)和全局最优解的拣货路径长度D(θ∗)进行比较，并更新算子的权重，从而完成一次内层的迭代。

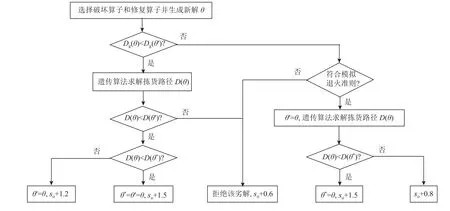
图6 ALNS算子分数更新流程图Figure 6 Flowchart of the ALNS operator score update process

3 数值实验

为了验证本文模型和算法的有效性，设计不同规模的测试算例对模型和算法进行实验。数值实验过程在AMD Ryzen 3500U CPU、8GB内存的笔记本电脑上运行，求解器使用Gurobi9.0商业求解器，启发式算法使用Python3.8实现。

设计带有1 000个储位的可移动仓储系统，将SKU随机分配至各个储位，生成100种SKU和200种SKU的仓库数据分别为S1000_K100和S1000_K200，在随机分配的过程中以一定的概率将相同的SKU分配在连续的l个储位上以形成一个长度为l的货架，并提前计算出储位间的距离矩阵。订单需求数据参考Silva等[15]使用的数据集，表2为使用的订单需求数据集，其中订单数表示需要完成拣选的订单数量，一个订单需要进行一次拣货操作；订单中需求数是每个订单中包含的不同SKU的数量；需求偏斜表示不同的需求分布，采用帕累托原则将SKU分为3类，偏斜的A/B/C表示少量SKU出现A%，中等SKU出现B%，大量SKU出现C%。

表2 订单需求数据集Table 2 Dataset of the order demand

为了验证ALNS算法在货架交换模型上求解的有效性，对不同的仓库数据和不同的订单数据集测试货架移动后的拣货效果，分别对比初始分布、Apriori移动初始解和ALNS移动结果下的拣货路径长度，其中总成本为拣货路径长度+移动货架的数量。表3为货架移动算法的对比，其中Opt表示求解结果；Move表示移动的储位数量；Dev表示算法较于前者的优化百分比。Apriori算法移动结果相较于初始的布局能够给拣货路径带来较大的优化，而ALNS算法的移动结果在有Apriori作为初始解的情况下有了进一步的优化，在移动货架的数量增多的情况下总成本也有所减小，代表实际的拣货路径有着较大程度的优化，在不同的仓库数据和不同的订单数据集中ALNS算法都有着不错的表现。以O10_I5_D3为例，ALNS算法目标函数为540，相较于初始解优化了26.8%，相较于初始分布优化了46.5%。ALNS算法的迭代过程如图7所示，其中蓝色线表示内层局部最优解的下降曲线，会伴随着模拟退火接受的劣解上下波动，而褐色线表示全局最优解的下降曲线。

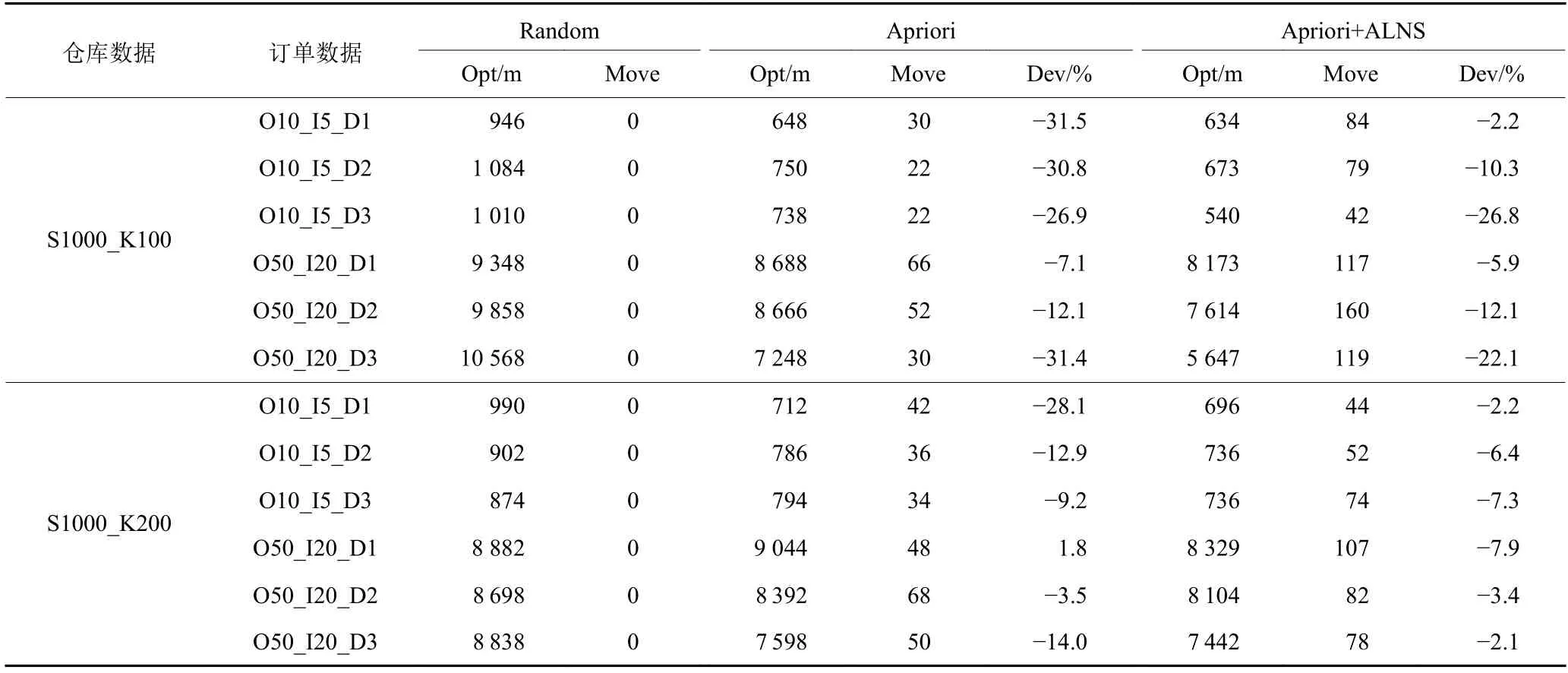
表3 货架移动算法对比Table 3 Comparison of shelf movement algorithms

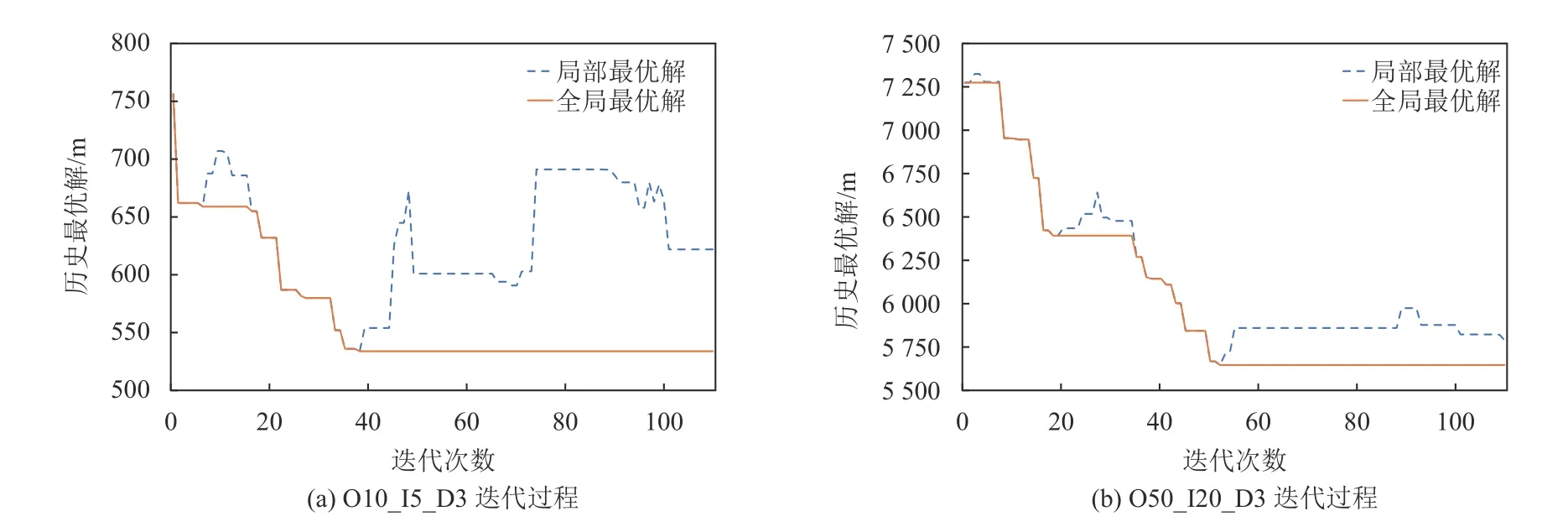
图7 ALNS算法迭代过程Figure 7 Iterative process of ALNS algorithm

在可移动仓储系统中，特别是在“人到货”的拣货模式下，没办法对货架进行特别频繁的移动操作，若没有AGV小车可能存在更高的人工移动成本，因此如何平衡货架移动频率和带来的拣货效率的提升是比较重要的。在实际应用中，仓库会累积一定数量的订单并分批次进行拣选作业，而决策时间可以表示为订单池中订单的累积时间。表4中记录了24 h内不同决策时间下进行货架移动的结果对比，仓库数据使用S1000_K100，共100个订单，每个订单20个需求SKU，将决策时间分为6 h、12 h和24 h，表示每过6 h、12 h、24 h，针对订单池中累计的订单进行一次货架移动模型求解。从不同决策时间的结果来看，24 h内决策次数越多，移动的货架总数越多，总体的拣货路径距离越短。如图8所示，拣货路径距离与货架移动数量总体呈反比，尽管看起来增加决策次数，通过移动大量的货架有着较好的拣货效率的提升，但实际上还要取决于不同仓库中移动货架更改仓库存储布局所带来的成本大小，即目标函数 (1) 中的p值。若使用AGV小车，则移动成本较小且移动速度较快，可以通过高频次的货架移动实现更大程度的拣货优化；若使用人工移动货架，成本较大且移动时间较长。因此需要考虑如何合理地制定决策次数，以平衡移动成本的增加和拣货成本的减小。从整体上来看，双层启发式算法在可移动仓储系统的拣货路径优化取得了较优的效果，通过ALNS算法结合模拟退火加强货架移动的邻域搜索能力，以GA算法完成邻域解的拣货路径的求解，并通过内外层的不断迭代，获得一个较优的货架移动和拣货方案。

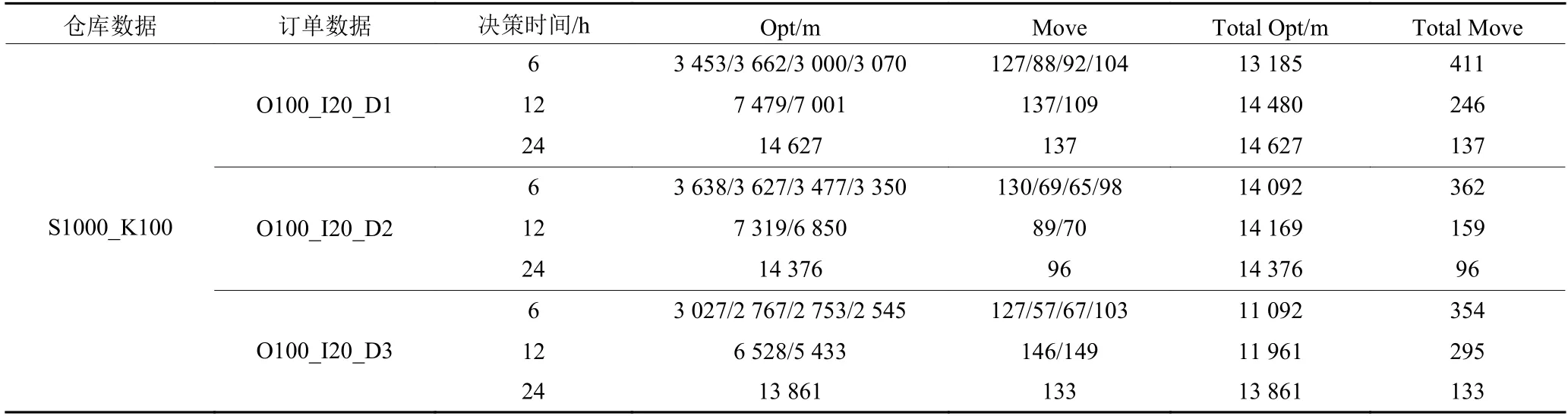
表4 不同决策阶段移动结果对比Table 4 Comparison of shelf movement results at different decision stages

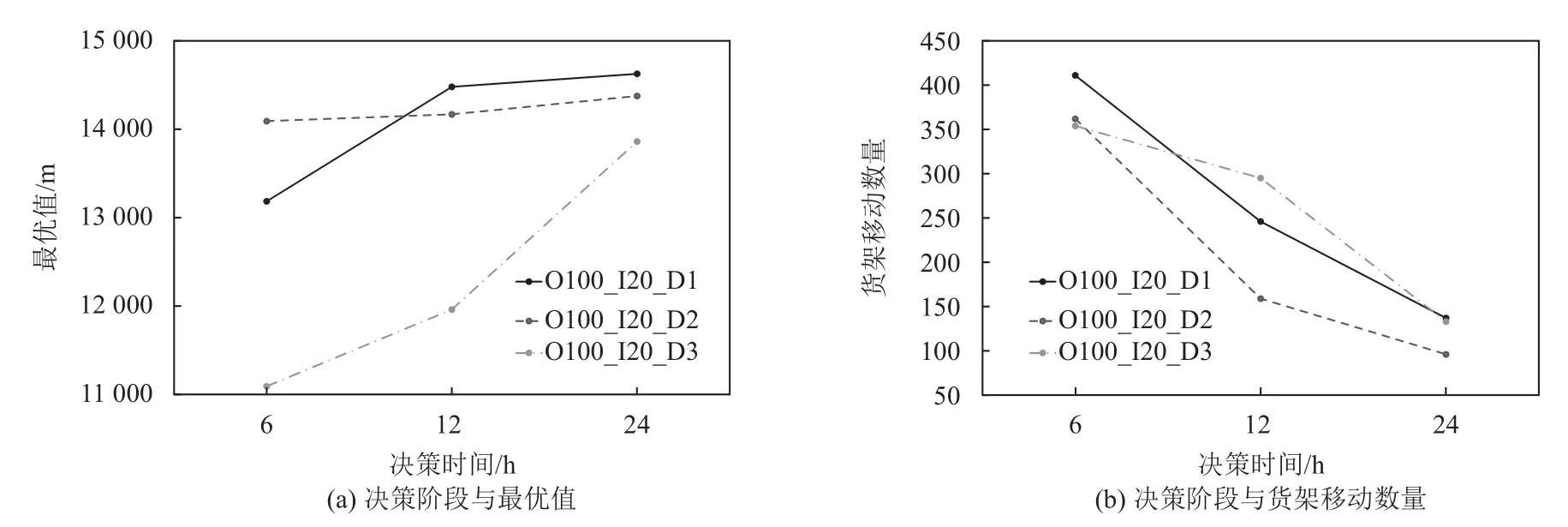
图8 ALNS算法不同决策阶段的结果Figure 8 Results of ALNS algorithm at different decision stages

4 结论

本文针对可移动货架下的储位选择与拣货路径联合优化问题，首次提出了双层的混合整数规划模型，包括下层订单拣货路径优化模型，上层货架移动优化模型。并通过双层的元启发式算法完成了对模型的求解，上下两层模型互相影响从而求解出最优的移动和拣货方案。最后使用不同规模的数值实验完成了算法的可行性和有效性验证，为可移动仓储系统提供了货架移动和拣货优化的新思路和新方法。