考虑不确定性条件的退役产品拆解柔性调度
马新一,匡增彧,卓晓军,任莹晖
(1.湖南大学 机械与运载工程学院,湖南 长沙 410082;2.长沙矿冶研究院有限责任公司,湖南 长沙 410012;3.同济大学 机械与能源工程学院,上海 201804)
随着我国经济和科技的发展,3C电子产品和新能源汽车等新兴消费品快速更新迭代,此类产品退役给环境保护、战略矿产资源需求和产业可持续发展带来巨大压力[1]。为实现我国“3060”双碳战略目标,促进环境和产业的可持续发展,梯次利用和资源化成为此类退役产品最佳的循环再利用方式[2-4]。但回收的退役产品来源复杂、品类和结构多样、性能残值不一,造成其循环再利用前的回收拆解深度、拆解序列和拆解方法不确定,导致回收拆解逆向生产调度受到诸多不确定性扰动因素影响[5]。
现阶段,我国退役产品回收拆解企业普遍存在生产自动化程度低、手工作业占比大、依赖人工经验排程等现状[5]。造成退役产品的拆解破损良率低、生产资源调度和拆解物料管控困难、存在环境污染和生产安全等瓶颈问题,影响了退役产品循环再利用的经济性[6]。为解决上述问题,考虑新兴消费产品内部结构同质化发展趋势,柔性工装拆解工作站逐渐成为退役产品大规模自动化拆解线的发展趋势。在考虑退役产品多源异构不确定性扰动因素条件下,如何构建退役产品拆解线生产的调度策略与模型,提升退役产品大规模自动化拆解线动态调度的平稳性,成为了回收拆解逆向生产亟待解决的关键问题。
对于传统的离散制造正向生产而言,常采用网络模型和参数假设等描述不确定生产工艺流程和工时节拍,构建不确定条件生产调度模型。例如,Tao等[7]利用AND/OR网络描述柔性车间中设备选择和工艺流程不确定问题。Zhang等[8]利用基于图的约束规划求解集成式工艺规划与车间调度问题。蒋胜龙等[9]针对加工时间不确定的炼钢—连铸调度,构建基于有向网络图的柔性调度模型。Amiri等[10]将具有不确定性的加工时长假设为随机且服从正态分布。正向生产多关注于加工时长或工艺流程等单一不确定性因素。而对于具有多源异构不确定性特性的退役产品回收拆解逆向生产而言,品类、结构、性能残值和拆解方式等不确定性扰动因素,通过对拆解深度、拆解序列和拆解方式的综合影响,转化为对拆解线生产资源组合和完成时间的动态扰动。因此,不确定性扰动因素对退役产品拆解线生产调度的动态平稳性影响更为复杂。
此外,柔性工装拆解工作站类自动化拆解线生产调度侧重生产资源的组合优化,具有典型NPhard问题属性。遗传算法、粒子群算法等是典型NP-hard问题求解常用智能算法。例如,姜天华[11]以生产市场最短和能耗最小为目标建立柔性作业车间进行生产调度模型,并采用灰狼优化算法求解。Liu等[12]为克服遗传算法准确性低的问题,提出可变邻域下降混合遗传算法 (VND-hGA),设计基于粒子群算法的遗传算子用于解决柔性车间调度问题。张晓星等[13]利用融合单亲遗传算法基因变异操作的改进混合蛙跳算法求解柔性车间调度问题。在现有求解NP-hard问题的诸多智能算法中,遗传算法与模拟退火等算法结合可以提高算法全局搜索能力,在生产调度等组合优化问题中证明了其有效性[14-16],更适合于不确定性条件下退役产品拆解线生产调度问题。
本文以退役动力电池回收拆解逆向生产为例,展开考虑不确定性因素的退役产品柔性拆解生产动态调度问题研究。构建基于AND/OR网络结构的退役产品柔性拆解线混合整数规划调度模型,改进融合单亲遗传和模拟退火机制的智能算法,最后实例验证模型和算法的可行性。
1 问题描述与建模
1.1 问题描述
本文研究采用柔性工装拆解工作站的退役产品拆解线生产调度问题,该问题描述如下。某批次中有k件退役工件J={J1,J2,···,Jk} 需要在mk台设备M={M1,M2,···,Mmk}上 进行拆解。每台设备Mm配有mf件配套夹具,夹具切换时间为Tm。每个工件Ji的拆解序列中有ni道工序Oi={Oi1,Oi2,···,Oini}。拆解序列中可能有多条可选的工艺路线,拆解时只能从中选择一条进行拆解,且拆解过程必须遵守工序紧前紧后关系。每道工序Oij都有一个拆解资源集Mij={Mij1,Mij2,···,},资源集中元素表示一种设备和夹具的组合方式。拆解时可以从拆解资源集中选择任意一种组合方式。退役产品拆解线生产调度以拆解时长最短为目标,模型建立前作出如下假设。
1) 所有设备在开始时刻都没有安装夹具,必须在安装相应夹具后才可以进行加工;
2) 每台设备某一时刻只能拆解一道工序,拆解过程不可中断;
3) 对任意设备,若前后两道工序的夹具不同,则需要计算夹具切换时间,否则无需切换夹具,可以连续加工;
4) 忽略工件在各工作站运输的时间,工件可以在各个工作站之间运输;
5) 不考虑能源消耗、成本约束等其他条件。
1.2 模型构建
1.2.1 AND/OR调度策略模型
为表示退役产品不确定的拆解深度和不确定的拆解线工艺路线等生产调度扰动因素,构建如图1所示的AND/OR节点网络调度策略模型。

图1 AND/OR节点网络示意图Figure 1 Diagram of an AND/OR node network
定义1节点。图1中用N={0,1,2,···,n+1}表示节点,节点代表工序。其中,0和n+1节点为虚拟节点,分别表示起始节点和终结节点。批次中每款退役工件拆解序列都从0节点出发,到n+1节点结束。0节点后多条退役工件拆解序列体现来料品类的不确定性。
定义2AND节点。图1中无阴影的节点表示AND节点。若选择AND节点代表工序,则该节点所有紧后节点工序都必须被选择。特别规定 0节点和n+1节点为AND节点。
定义3OR节点。图1中灰色阴影节点表示OR节点。若选择OR节点代表工序,则该节点所有紧后节点工序中仅能选择一个进行加工。
定义4可选活动链。用 CH 表示退役产品拆解序列中可选的工艺路线,如图1的AND/OR模型,CH1={{3,4,5,6,7},{8,9,10}},CH2={{4,5},{6}},CH3={{14},{15}}可分别表示为3组可选活动链。
AND/OR网络的可选活动链构成具有树状结构层级关系,如图2所示。AND/OR节点网络图的可选活动链均可绘制成至少3层的树状结构图。第1层表示所有位于可选活动链中的节点集合;第2层表示互相独立的可选活动链集合;从第3层开始则是各个可选活动链集合的活动链子集,用于表示各活动链的包含关系。

图2 可选活动链树状结构示例Figure 2 The tree structure of an optional activity chain
1.2.2 基于AND/OR节点网络的拆解调度模型
1) 索引与参数。
i、j为工序索引,i,j∈{0,1,2,···,n,n+1},n为退役产品拆解工序总数;m为拆解设备索引,m∈{1,2,···,mk},mk为设备总数;f为夹具索引,f∈{1,2,···,mf},mf为设备Mm的配套夹具数,需与设备索引联合使用;t为时刻索引,t∈Γ={0,1,2,···},Γ 为时刻集 合;Aij为工序紧前关系 参数,0-1变量,若i是j紧前工序则为1,否则为0;γi为节点性质参数,0-1变量,若i节点是AND节点则为1,否则为0;Tm为设备Mm切换夹具所需的时间;Di,m,f为工序i使用机器Mm上夹具f的拆解时间;Ω为充分大的实数。
2) 决策变量。
xi为工序选择变量,0-1变量,若工序i被选中则为1,否则为0;yi,t为工序完成时刻变量,0-1变量,若工序i在t时刻完成则为1,否则为0;zi,m,f为设备夹具选择变量,0-1变量,若工序i使用机器Mm上夹具f则为1,否则为0;Bm,i,j为机器工序顺序判定变量,0-1变量,对机器Mm,若工序i是j紧前工序则为1,否则为0;Cm,i,j为机器工序夹具判定规则,0-1变量,对机器Mm,若工序i和j夹具不同则为1,否则为0。
3) 目标函数。
以退役产品回收拆解最短完工时长为调度优化目标。
4) 约束条件。
其中,式(2) 为工序拆解方式选择约束;式 (3)为工序拆解次数约束;式 (4) 为AND和OR节点性质约束;式 (5) 为各工件拆解顺序约束;式 (6) 为机器操作时间约束,考虑夹具切换的时间;式 (7) 表示设备初始时刻必须先装载夹具再进行第1道工序加工;式 (8) 和式 (9) 为Bm,i,j和Cm,i,j变量描述,当工序选择变量xi、完成时刻变量yi,t、设备夹具选择变量zi,m,f和拆解时长参数Di,m,f确定时,Bm,i,j和Cm,i,j变量的值也唯一确定。
2 算法设计
考虑到AND/OR节点网络的编码方式,若通过标准遗传算法中2个父代交叉获得子代,容易违反工序紧前紧后关系而生成非可行调度方案。单亲遗传算法 (partheno-genetic algorithm,PGA) 具有与标准遗传算法类似的进化机制,去除了标准遗传算法中的交叉算子,具有全局收敛性[17],可用于解决组合调度优化问题[18]。与标准遗传算法类似,单亲遗传算法同样具有易陷入局部最优的缺陷。因此本文融合模拟退火算 法 (simulated annealing,SA) 机制,提出模拟退火单亲遗传算法 (SA-PGA) 求解基于AND/OR节点网络的拆解调度模型。其算法流程如图3所示。其中,α为温变系数,CT为当前温度,TEMPf为外循环最高温度,Gen为当前迭代次数,L为内循环最大迭代次数。在选择个体变异时引入SA机制,以一定概率接受较差解进行变异,提高算法全局搜索能力。
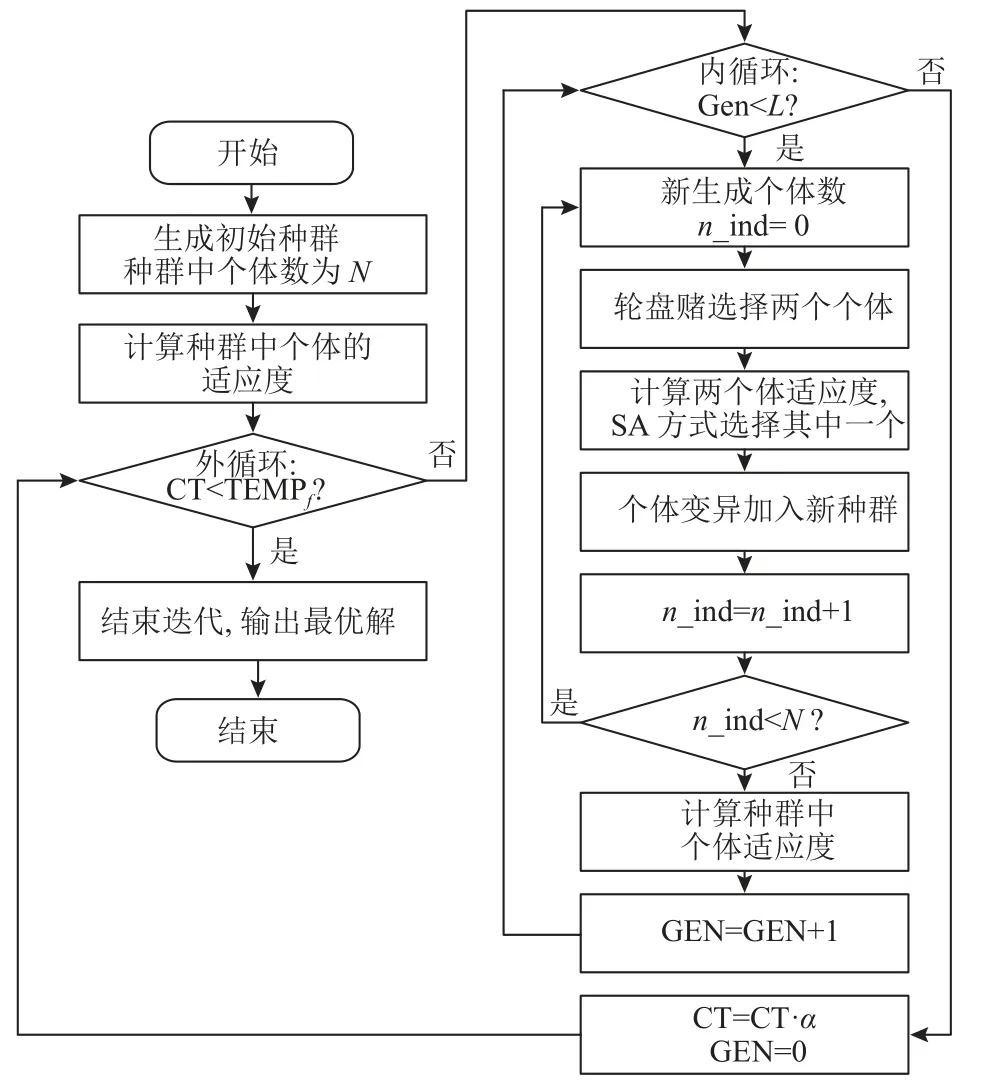
图3 算法流程Figure 3 Flow chart of the algorithm
2.1 编码设计
由于退役产品的多源异构特性,拆解时需要先针对不确定的拆解深度和拆解序列进行工序选择和排序,再对每道工序不确定的拆解方法进行设备和夹具选择。因此,需构建如图4所示的四子串实数编码。第1层为工序层,首尾分别为初始节点和终节点,中间节点表示工序的加工顺序,需符合紧前关系约束。第2层为选择层,编码表示对应第1层工序的选择与否,规定初始节点和终节点都被选择。第3层和第4层分别为设备层和夹具层,表示被选择节点所代表的工序的加工设备和夹具,未被选择的节点、初始节点和终节点则无需选择设备夹具组合,该处基因编码为0。
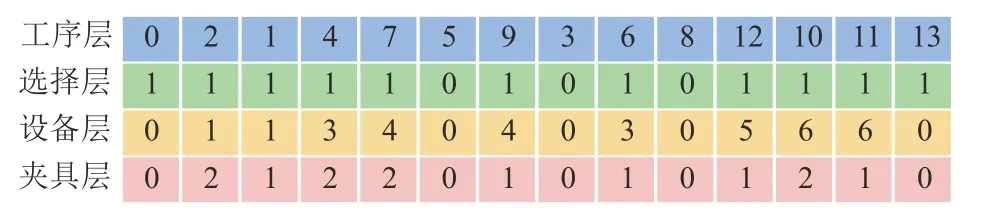
图4 四子串实数编码示例Figure 4 An example of four substring real number coding
2.2 遗传算子
单亲遗传算法的遗传算子可以分为基因重组算子和基因突变算子两大类,其中基因重组算子是指基因的位移或换位。本问题的四子串编码中工序和选择层的遗传变异,也将采用基因重组算子与基因突变算子进行变异。本文设计的基因重组算子包括循环位移算子,基因突变算子包括选择变异算子和设备夹具变异算子。变异流程如图5所示。当随机选择节点代表的工序被选择的时候,则采用循环位移算子进行变异操作。循环位移算子的作用是在符合工序紧前关系的前提下,将被选中的节点放到其紧前工序和紧后工序之间的新位置,改变工序的操作顺序。图6为循环位移算子示例,随机选择节点6进行移动,记录下其坐标值最大的紧前工序和坐标值最小的紧后工序坐标,即节点7和节点10的坐标,并从两者之间随机挑选一个坐标成为6节点新的位置,其他节点顺位移动。
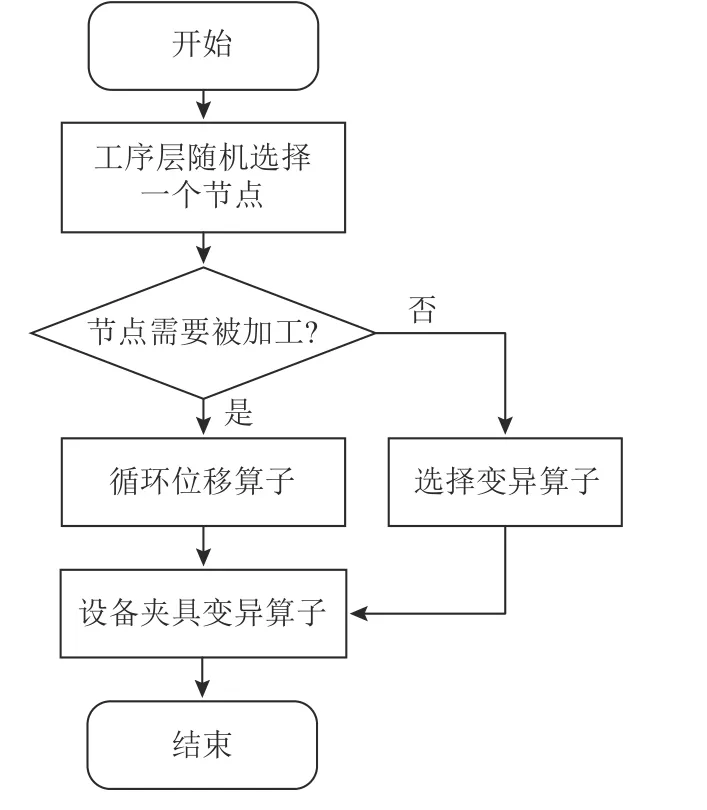
图5 个体变异流程Figure 5 Individual mutation process

图6 循环位移算子Figure 6 Cyclic shift operator
当随机选择节点代表的工序未被加工时采用选择变异算子。如图7所示,已知被选中的节点3和节点8位于同一条未被选择的活动链中,且与节点6在同一可选活动链集合中,则选择位移算子就会选中节点3和节点8所在的活动链,实现加工工序的改变。在可选活动链树状结构中,选择变异算子将按照等级从高到低逐级对活动链进行选择,直到最底层活动链被选择为止。实现选择链变换后,对新选中的节点随机分配设备和夹具。当工序层和选择层的循环位移算子和选择变异算子执行后,采用多点变异方式对设备和夹具进行变异。

图7 选择变异算子Figure 7 Mutation operator of selection
2.3 模拟退火机制
传统的遗传算法多采用轮盘赌方式选择个体,容易导致优秀个体流失。在单亲遗传算法中引入模拟退火机制,可以一定概率接受较差的解,有效防止算法出现“早熟”现象而陷入局部最优。本文采用二元锦标赛融合模拟退火的方式选择个体进行变异操作。
1) 采用轮盘赌方式在种群中选择两个个体ind1和ind2,计算其完工时长分别为 Fit(ind1)和Fit(ind2)。
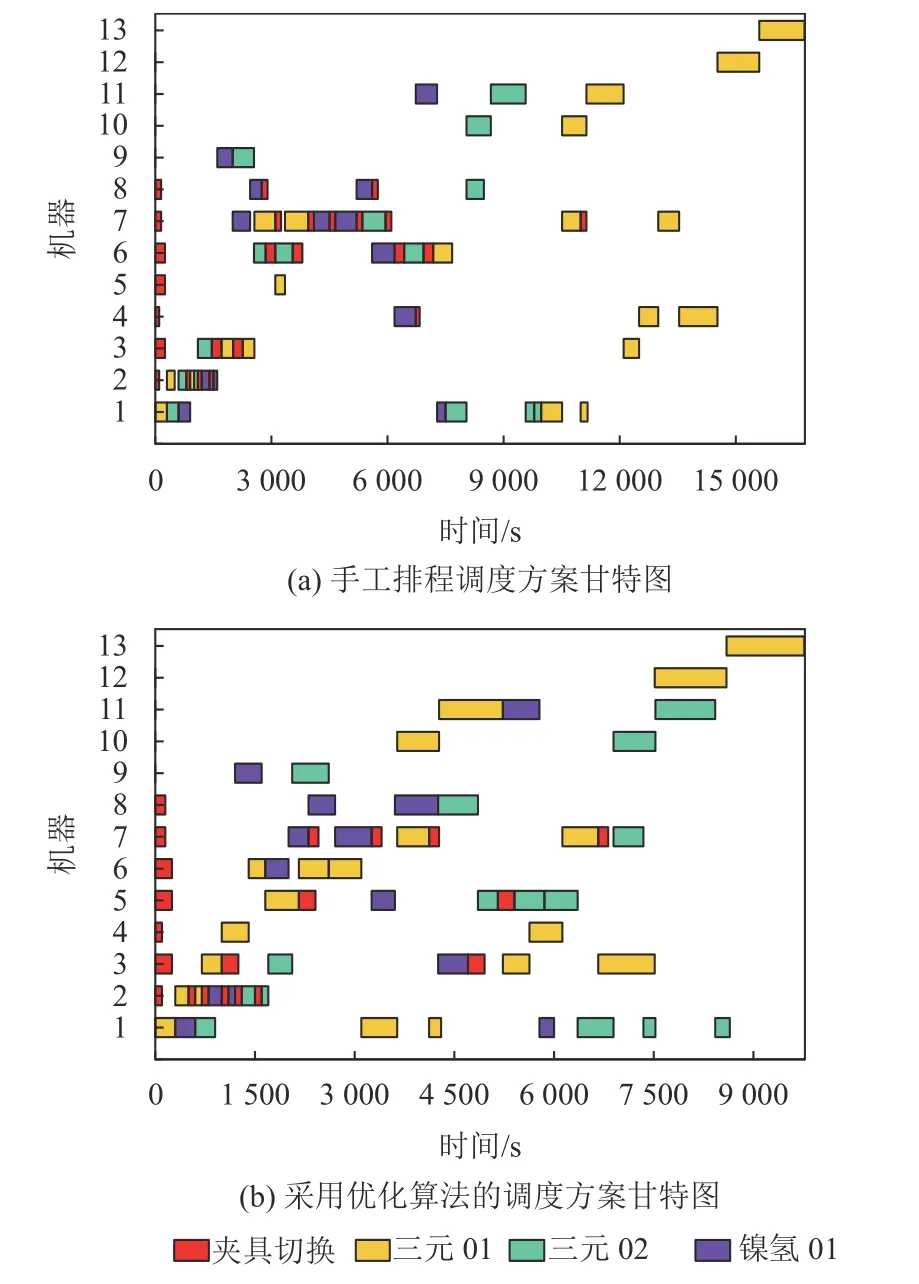
2) 依据模拟退火中Metropolis准则接受个体,若Fit(ind1) 3) 重复1)、2),直到新种群中个体数量与原种群相同。 以某企业退役动力电池的回收拆解为例,验证柔性拆解线动态调度策略和模型的可行性。新能源车常用的动力电池类型包括磷酸铁锂电池、锰酸锂电池、镍氢和三元材料电池等。传统动力电池具有电芯-模组-电池包三级结构,新型动力电池朝无模组、集成化结构化创新。在电芯层面又有刀片电池和大圆柱电池的区别。由于动力电池退役后仍有70%容量可用于梯次利用,且动力电池包含镍、钴、锰等重金属元素可资源化再利用,有助于节省动力电池上游贵金属资源消耗。因此,回收的退役动力电池从来源、类型、结构和性能残值等方面都存在不确定性。 退役动力电池类型和结构的不确定将影响拆解序列的不确定,导致拆解方法和拆解动作顺序不确定。其性能残值的不确定,将影响循环再利用流向的不确定,导致拆解深度和拆解序列的不确定。外观结构的完好和破损情况,也会影响选择手工或机器拆解方式的不确定,导致拆解时间变动带来总完工时间的不确定。本文选取某公司的退役动力电池回收拆解柔性线为例,考虑拆解深度、拆解序列和拆解方法为不确定性扰动因素,与单亲遗传算法相比较验证本文改进的模拟退火单亲遗传算法的有效性,与现阶段广泛采用的调度员手工调度比较,验证本文构建的拆解调度模型实用性。 选择包含两款三元动力电池 (三元01、三元02)和一款镍氢动力电池 (镍氢01) 的拆解批次。拆解线中设备和工位信息汇总如表1所示。设置龙门吊负责电池包和模组的上下线。漏电检测、扫码、手动维护开关、拆安全包开关、放电等难以使用机器操作的工序采用人工处理。设置了2台带视觉识别功能的拆解机器人工位,负责拆解螺母、螺栓类紧固件。考虑拆解安全性,由人工工位负责拆解可能存在内部结构破损或变形的退役动力电池。表2~ 4分别列出了实例中3款动力电池各工序所需的拆解设备、夹具以及相应工序时间信息。部分工序的前序工序和后续工序相同,如三元01的工序6、7、8和工序15、16,表示该些工序顺序可互换,无紧前紧后约束。在调度过程中,需要合理配置各个工序的设备和夹具,合理安排各工序的操作顺序。与定工序调度相比,相互之间没有紧前紧后关系的工序,拆解调度复杂度会更高。 表1 拆解线设备工位信息表Table 1 The station information of disassembly line equipments 表2 三元01拆解工序信息表Table 2 Disassembly sequences of ternary power battery 01 表3 三元02拆解工序信息表Table 3 Disassembly sequences of ternary power battery 02 表4 镍氢01拆解工序信息表Table 4 Disassembly sequences of Ni-MH power battery 01 当前,采用调度员手工排程随机调度,没有固定的调度规则和调度算法。本文采用在遵守设备拆解紧前紧后约束的条件下随机生成调度方案的形式描述当前的手工排程调度方法。为减少偶然性,测试50次得到调度方案平均拆解时长。再根据拆解线基础数据 (见表2~ 4) 绘制调度策略AND/OR节点网络模型图,并采用PGA算法和SA-PGA算法求解。设置PGA算法和SA-PGA算法参数,设备变异率Pm=0.1,工序变异 率Pc=0.1,种群 数N=40,SA-PGA内循环迭代次数L=40,初始温度 TEMP=120◦C,终温T EMPf=1◦C,温变系数α=0.95。 结果表明,模拟调度员手工调度的50次试验中,最大完工时长为18 020 s,最短完工时长为10 710 s,平均完工时长13 829.8 s,极差为7 310 s,方差为2 875 973 s2。本文调度模型PGA算法和SAPGA算法求解运行的迭代曲线如图8所示。由图8可知,PGA算法寻得最优方案的完工时长为9 860 s,劣于SA-PGA算法寻得的9 765 s的调度方案。说明SA-PGA算法继承了PGA算法收敛速度快的优点,同时也能够跳出局部最优。 图8 PGA与SA-PGA迭代曲线Figure 8 Iterative curves of PGA and SA-PGA 基于SA-PGA算法的50次测试中,迭代完成后种群中最长完工时间为10 365 s,最短完工时长为9 765 s,平均完工时长为9 829.3 s,极差为600 s,方差为19 750 s2。与手动调度相比,采用AND/OR节点模型和优化算法后,调度结果的方差和极差明显减小,调度波动更小,且完工时长明显缩短,平均完工时长缩短27.4%,说明了调度模型的有效性和鲁棒性。 对比优化前后调度方案甘特图,手工排程完工时长为16 775 s时的调度方案如图9 (a),采用本文提出调度模型及改进算法获得的完工时长为9 765 s的调度方案如图9 (b),两种调度方法相关结果如表5所示。结合图9与表5可知,采用优化算法后,设备利用率更加均衡。例如,优化后用于相同拆螺母工序的视觉识别机器人2的设备5和设备6分别工作了2 150 s和1 540 s,而优化前采用手工调度方式时设备5仅工作250 s,远小于设备6的 2 320 s,存在利用率低的问题。优化前后夹具切换次数由25次减少到20次,夹具切换时长由4 350 s缩短至3 350 s,减少了时间浪费。 表5 优化前后调度方案数据汇总表Table 5 Data of dispatching schemes before and after optimization 图9 优化前后调度方案甘特图和图例Figure 9 Gantt chart of scheduling schemes before and after optimization 在该拆解线中,表示人工拆解螺栓和螺母的设备4、7和8,主要负责破损严重无法使用机器拆解的工序,以及机器被占用时的手工拆解。当电池部件破损较轻可以使用机器拆解时,人工拆解工位与代表视觉识别机器人的设备3、5和6存在可相互替代的关系。由于电池结构复杂和工人操作熟练度等因素,使人工拆解相比视觉识别机器人拆解时长较长。传统手工调度难以平衡机器和人工的工作负荷,容易产生机器闲置率高的问题。采用优化算法后,表示人工工位的设备4、7和8拆解时长由7 345 s减少至4 870 s,代表视觉识别机器人的设备3、5和6拆解时长由3 930 s增加至6 050 s。机器工作时长在所有工位工作时长占比由44.4%提高到69.9%。由机器代替手工拆解,提高了拆解线的拆解效率和自动化利用程度。 针对不确定条件下的退役产品柔性拆解动态调度问题,构建基于AND/OR节点网络退役产品拆解调度模型。设计了四子串编码规则和循环位移、变异选择和设备夹具变异3种遗传算子,提出将模拟退火机制与单亲遗传算法融合的SA-PGA算法求解调度问题。 在实例验证中,与模拟手工排程的随机调度相比,本文提出的调度方案完工时长缩短27.4%,自动化率提高25.2%。设备的工作负荷得到平衡,夹具切换造成的时间浪费缩短,实例验证调度方法具有可行性。在来料品类、拆解序列和拆解方式等不确定扰动因素影响下,多次调度的完工时长方差减小。本文提出的调度模型有助于减小不确定性扰动因素对拆解调度的影响,具有鲁棒性,实现对柔性拆解设备和夹具的动态优化配置。 在建立调度模型时未考虑资源约束、工件运输时长等因素,因此综合考虑车间中其他因素对调度产生影响将是下一步研究的重点。未来可考虑将AND/OR节点调度方法集成到 MES 系统中,在拆解前输入相关基础数据,对拆解提供调度方案指导。3 实例验证
3.1 实例数据与参数设置
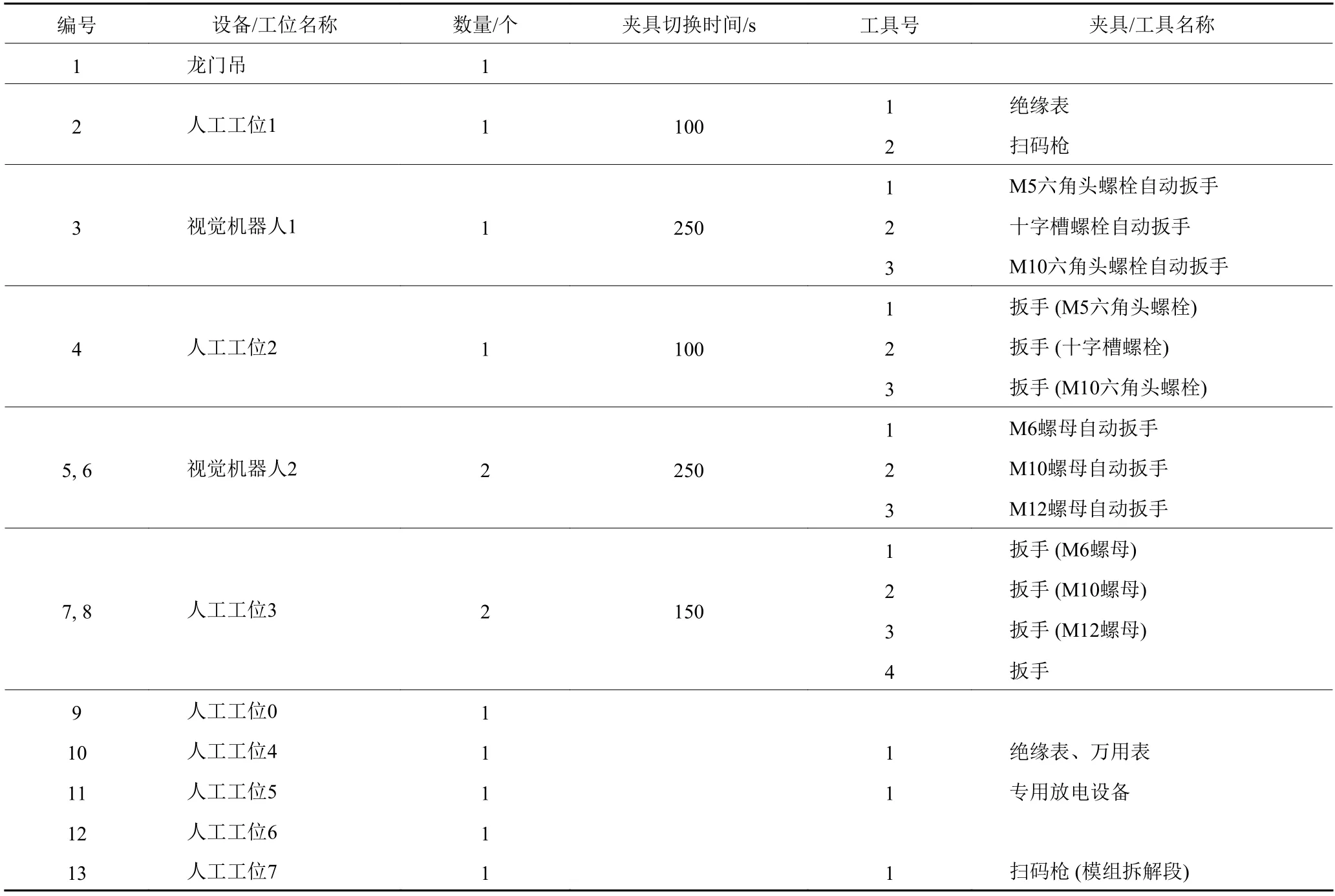
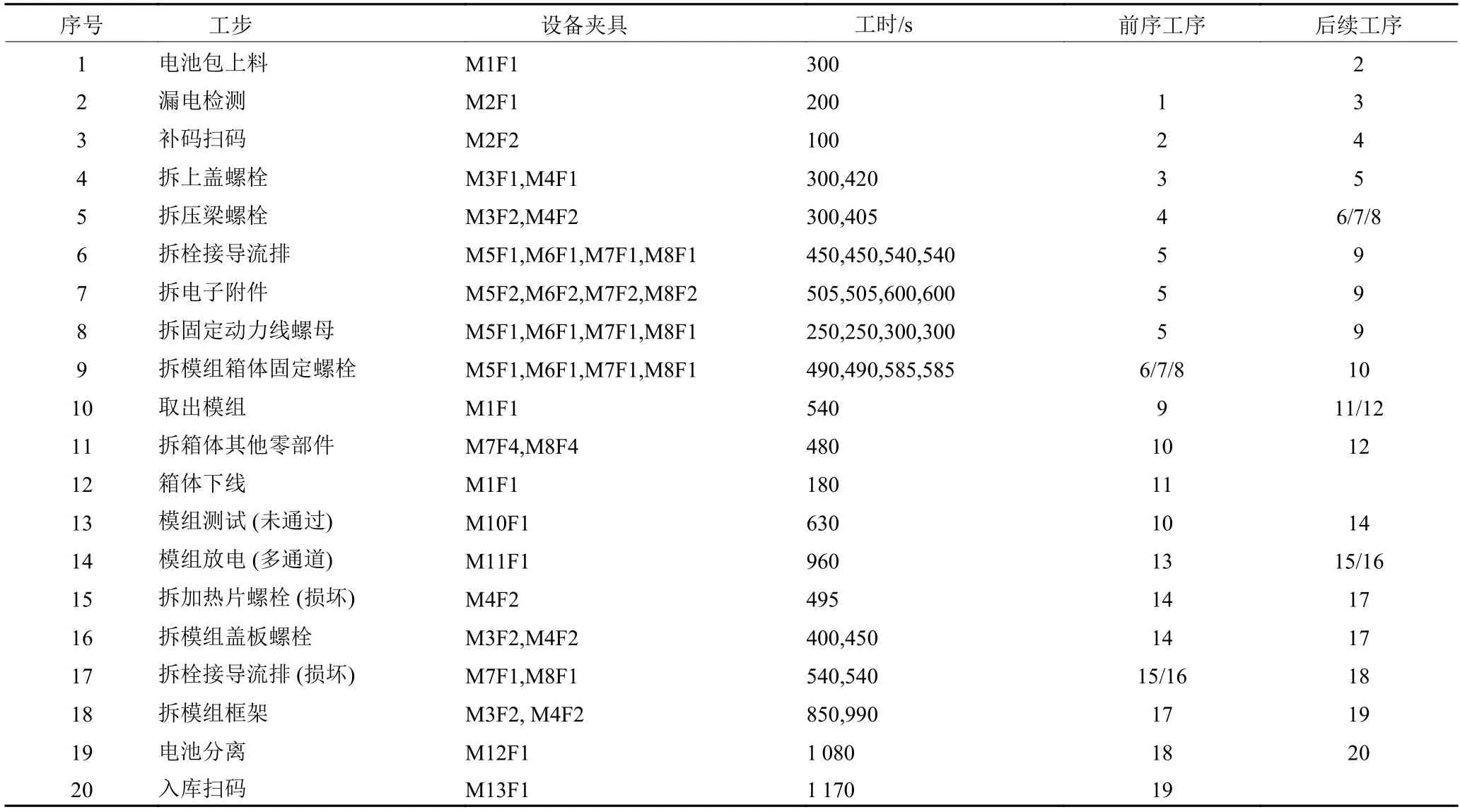
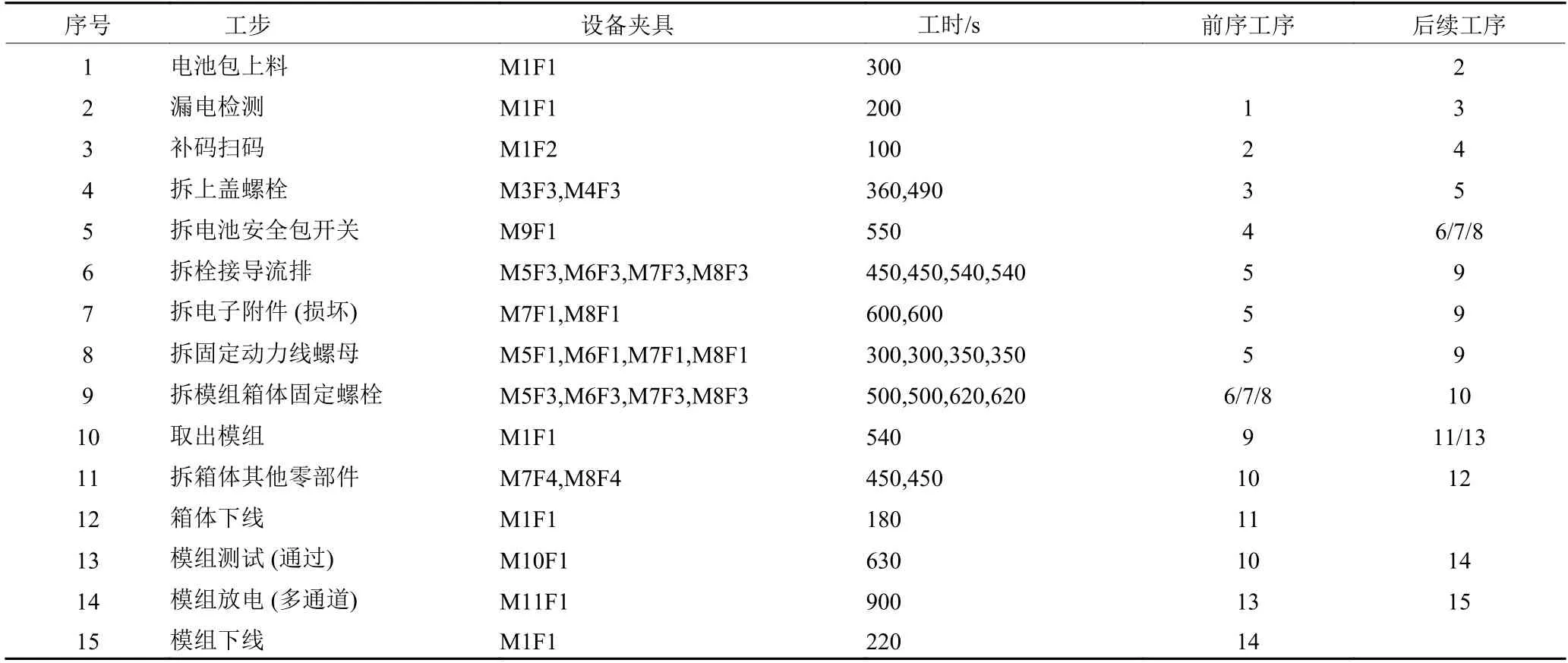
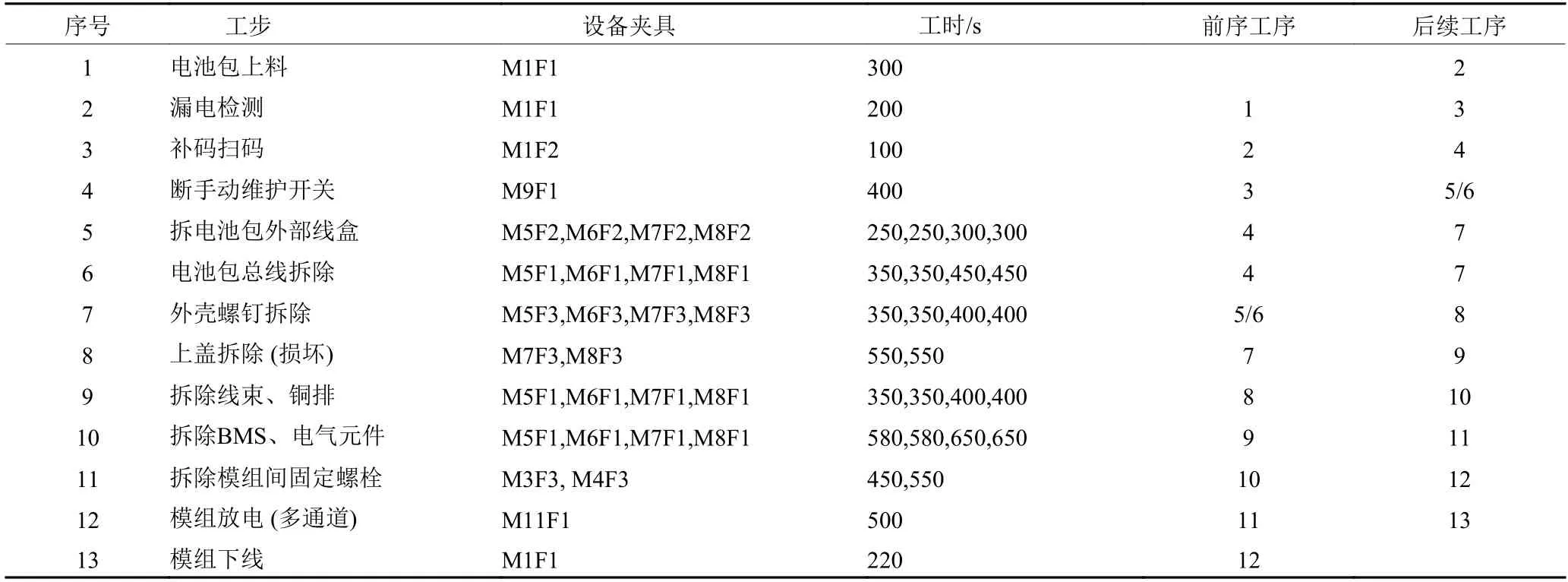
3.2 优化结果分析

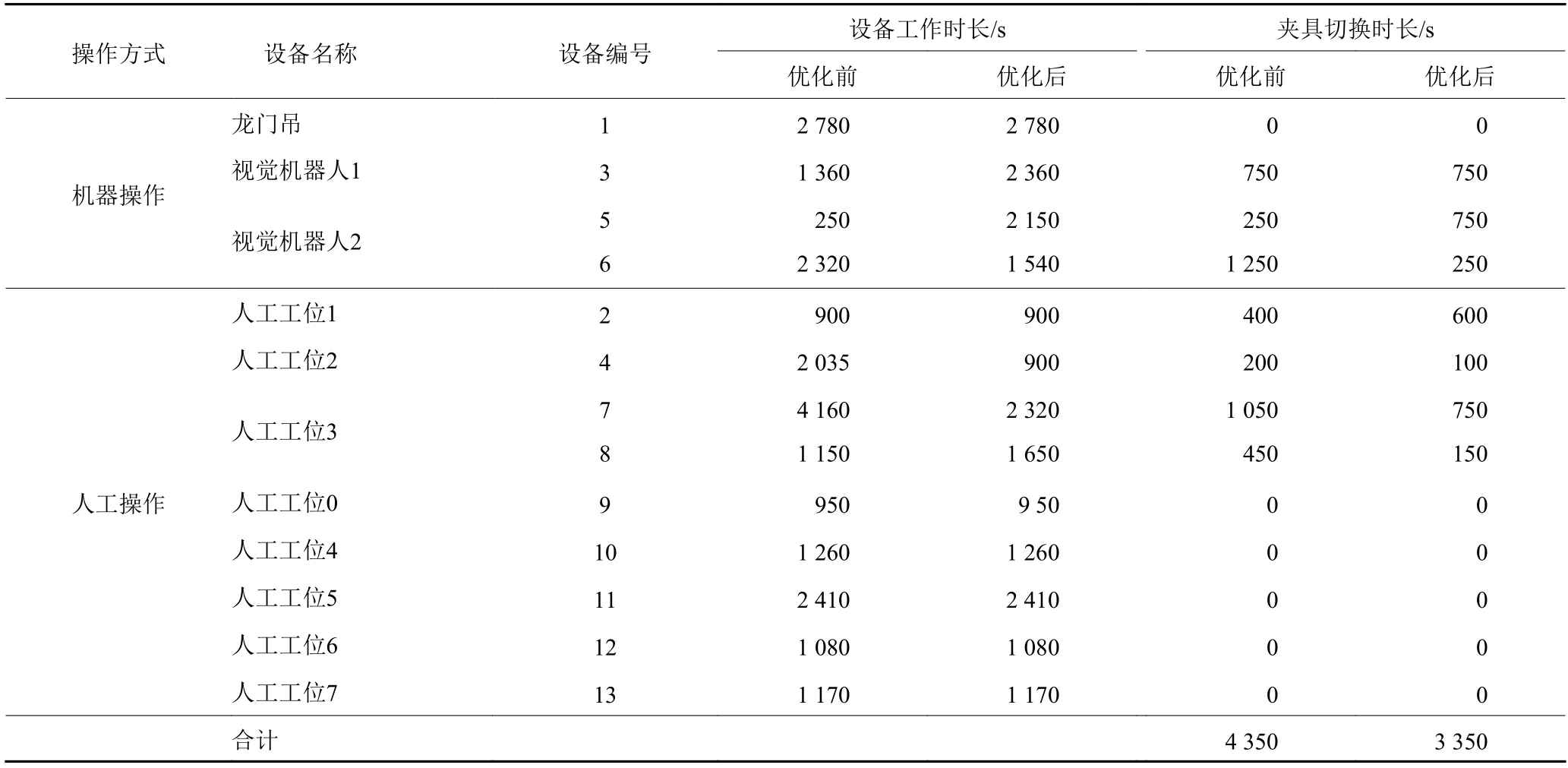
4 结论

