直觉感知、逻辑推理与数学运算在概率求解中交相辉映
程汉波 朱华伟
(1.广州市第二中学 510530;2.深圳中学 518000)
与大多数数学分支的发展历程类似,概率论也是从最初的直觉感知逐渐走向了逻辑性更强的符号化、形式化和公理化.概率论的诞生可追溯至帕斯卡、费马、惠更斯等在通信往来中讨论的一些博弈问题.当时人们对这些博弈问题中事件发生可能性大小的直觉感知出现困难或产生争论而求教于数学家,而数学家在通信往来的讨论与研究中逐渐建立了概率论中一些基本概念,如样本点、样本空间、随机事件、概率、数学期望等,利用概率的度量(数值)刻画随机事件发生的可能性,并基于逻辑推理与数学运算总结出一些概率模型,使得概率的计算变得有章可循.之后,在对伯努利概型的深入研究中,发现了两种形式的极限定理——大数定律和中心极限定理,奠定了概率论在数学中的理论地位,这个时期对概率论作出重要贡献的数学家有伯努利、棣莫弗、拉普拉斯、高斯和泊松等.然后,概率论的严格基础被建立起来,古典问题得到解决和深化,随机过程成为新的主题,研究领域明显扩大,内涵大为加深,期间柯尔莫戈洛夫等前苏联数学家起了主导作用.
然而,不论现在概率理论如何抽象,逻辑推理与数学运算之前的直觉感知都依然具有不可替代的作用.正如数学大师克莱因曾指出的:“数学不是依靠在逻辑上,而是依靠在正确的直观上,数学的直观是对概念、证明的本质把握.”我国曾师从数学大师柯尔莫戈洛夫的王梓坤院士也曾指出:“在实践中所体会到的直观形象有助于抓住本质,它常常是理论的先导,并为理论提供思路、模型与方法,严格的逻辑证明和计算有时无非是直觉的一种数学加工和精确化而已.”国家《义务教育数学课程标准》研制组组长、《普通高中数学课程标准》修订组组长史宁中教授也多次谈到:“数学结论的发现,依赖的并不是一般性,也不是严谨性,而是个人直觉.”并针对中学教学实际一针见血地批评道:“在我们现行的数学教学中,过分强调了演绎推理而忽略了归纳推理,过分强调了证明而忽略了命题的提出以及对命题的直观理解.”
由历史相似性原理知,概率论发展的历程与学生学习的过程存在相似性.一方面,直觉感知在概率的理解与计算中扮演着十分重要的角色,如掷硬币、掷骰子、摸球等古典概型试验中每个样本点等可能性的理解就是先有直觉感知后才有统计频率的验证.另一方面,逻辑推理与数学运算在随机事件概率的计算中也极为重要,这在建立起互斥、对立、相互独立事件及其概率运算性质,并积累了一些特殊类型的概率分布知识后尤为明显,因为据此使得概率计算便于模式识别且有章可循.这启发我们在概率计算问题的教学中既要追寻直觉感知背后的逻辑推理或数学运算,也要感悟逻辑推理或数学运算前面的直觉感知,以期在直觉感知、逻辑推理与数学运算的交相辉映中促进学生思维的提升与发展.本文结合概率论中经典的掷硬币与摸球模型中的具体实例,谈一谈直觉感知、逻辑推理与数学运算在随机事件概率求解中的重要作用及其对教学的启示.
1 正确直觉感知、逻辑推理和数学运算相互验证
直觉是逻辑的先导,逻辑是直觉的护栏.直觉不仅先于逻辑,而且为逻辑提供目标与方向,策略与方法.但是,直觉不能保证严格性,甚或不能保证正确性,这就需要逻辑的保驾护航以确定直觉的可靠性.以下问题来自复旦大学李贤平教授所著教材《概率论基础》(第三版)中的一道例题.
例1甲有n+1枚硬币,乙有n枚硬币,双方投掷之后进行比较,求甲掷出的正面数比乙掷出的正面数多的概率.
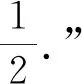
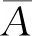
然而,笔者在教学实践中发现,学生对该简便解法的接受程度两极分化较为明显,领略其精妙者对其赞赏有加,但是还有相当一部分学生认为该解法并不自然,难以想到,就像“兔子是从帽子中变出来的”.近期笔者发现该问题出现在了武汉市2023届高中毕业生四月调考第20题中,据调查,在添加了题干和第一问提示引导的条件下,大量学生也没有想到以上解法.与之形成对比的是,大家普遍觉得利用分类讨论思想进行数学运算是更自然的想法,但是,恒等变形的技巧及过程的繁杂使得能够一气呵成给出完整解答者极少.下面给出学生利用数学运算得到的解法.
甲掷出的正面数比乙掷出的正面数多,可按甲掷出的正面数进行如下分类:
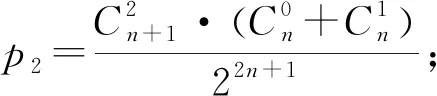
依次地,若甲掷出的正面数为n+1,则乙掷出的正面数可以为0,1,2,…,n,其概率为
由互斥事件的概率加法公式可得,甲掷出的正面数比乙掷出的正面数多的概率为
P=p1+p2+…+pn+pn+1
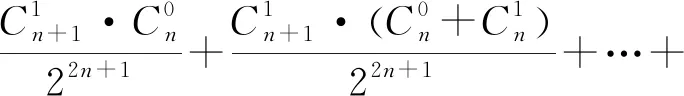
注意到对任意k=1,2,…,n,有



则
则由倒序相加法可知
2P=(p1+pn)+(p2+pn-1)+…+(pn+p1)+2pn+1
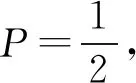
可见,数学运算的详细过程既验证了直觉感知结果的正确性,也进一步反映了逻辑推理解法简洁性的难能可贵.其实,概率求解问题中直觉感知、逻辑推理往往是从内隐的形象、感觉和经验出发,其思维特点为直观想象、灵感与顿悟,以简略浓缩的方式从结果上洞察问题的本质;而数学运算往往从外显的概念、命题和原理出发,其思维特点为严谨与理性,以连续完整的方式从过程上推演问题的结果.在日常教学实践中,师生的思维特点不尽相同,各有所长,受持续长久概率计算训练的影响,无意识或不自觉地倾向于从数学运算的视角出发去考虑问题不在少数.尽管如此,错误还是有可能存在的,尤其是当数学运算冗长且复杂的时候,更需谨慎.因此,最好能从直觉感知和逻辑推理的视角进行验证,而且这也是培养师生直觉感知能力的绝佳良机.正如数学大师波利亚在谈及解题四个阶段中的最后一阶段回顾总结时曾说:“如果存在着一些快捷而直观的步骤可用于检验结果或论证时,尤其不应该忽视它.”一系列引人联想与深思的反问句“你能检验这个结果吗?你能检验这个论证吗?你能以不同的方式推导这个结果吗?你能一眼看出它来吗?你能在别的什么题目利用这个结果或这种方法吗?”可见波利亚对数学运算的直觉感知和逻辑推理之重视程度.下例是笔者曾在数学竞赛测试中给学生测验过的一道题目.
例2口袋中有a个黑球,b个白球,它们除颜色不同外,其它方面没有差别,现在从口袋中随机地逐个摸球,直到袋中剩下的球全是同色球为止,求袋中剩下的球全是黑球的概率.
该题来自李贤平教授编著的《概率论基础学习指导书》,当时难住了绝大部分学生,某数学资优生利用分类讨论思想进行数学运算得到以下解法.
依次地,若最后剩下a个黑球,则倒数第a+1个一定为白球,其概率为
由互斥事件的概率加法公式可得,袋中剩下的球全是黑球的概率为
P=p1+p2+…+pa
注意到组合恒等式
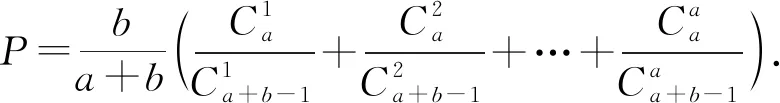
又注意到组合恒等式
可从组合数实际意义的视角进行理解与证明),
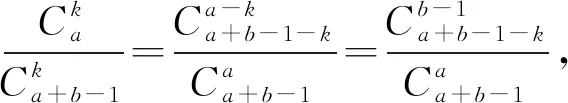
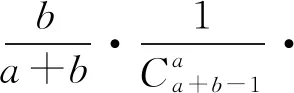
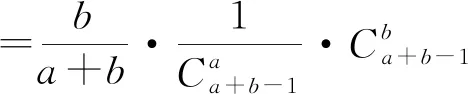
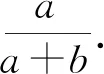
可见,对数学运算所得结果的直觉感知和逻辑推理解读是解题能力提升中不可缺少的环节.正如波利亚所指出的:“即便是相当优秀的学生,在得到了题目的解答,并将整个论证简洁地写下来以后,就合上书去做别的事情,这会遗漏掉通过回顾完整的答案,重新斟酌、审查结果与导致结果的途径以巩固知识提升能力的有益阶段.”一个循循善诱的良师,必将使他的学生深刻地认识到:任何一道题目在其解答完成之后,只要经过充分的研究和洞察,其解题方法往往可以加以改进,或最起码可以深化对答案的理解.
另外还应注意到,数学运算在概率求解中也并不是一帆风顺或万能的,比如,我们可将例2改编为以下例3.
例3甲袋中有a个黑球,b个白球,乙袋和丙袋都是空袋,先从甲袋中随机摸n(1≤n≤a+b)个球放入乙袋,再从乙袋中随机摸m(1≤m≤n)个球放入丙袋,最后从丙袋中任取一个球,求该球是黑球的概率.
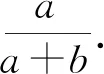
而且,若将眼光不局限于乙袋和丙袋中黑球与白球个数的随机性,而是聚焦于乙袋和丙袋中黑球与白球个数数学期望的稳定性,从整体上进行逻辑推理,可以得到以下解法.
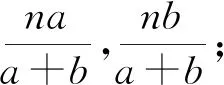
可见,面对复杂的概率求解问题,不要盲目地从数学运算开始,可先从直觉感知上熟悉问题,形成猜测,再从逻辑推理上分析问题,证明猜测,有时会起到事半功倍的效果.
另外,对于例2和例3,可能有人面对直观感知、逻辑推理解法的简洁与数学运算的复杂乃至困难形成的鲜明对比,会由此怀疑逻辑推理的严谨性,这种质疑的精神值得肯定,但要注意的是决定严谨性的并不是解答过程的长度,而是推理的逻辑是否有漏洞,正如数学大师希尔伯特曾经所指出的:“视证明的严格性为简洁性之敌人的观点是错误的,相反地,大量的事例使我们确信严格的方法同时也是简洁而易于理解的方法,正是我们力求严格,我们才必须去寻找简洁的证明方法.”这对我们在方法论的认识上具有重要的教育意义.
2 错误直觉感知的逻辑推理和数学运算双重驳斥
直觉感知有“功”也有“过”,或是由于已有数学经验的局限性,生活经验的误导,对概念、原理和逻辑的不恰当运用,以及不当的心理暗示与思维定势等原因,直觉感知有时难免会产生错误,这时逻辑推理或数学运算的护栏作用便得以凸显,也使得概率理论变得更严谨的同时其应用领域也不断扩大.正如布鲁姆曾指出的:“直觉的方式常常会产生错误的答案,这就需要一位敏感的教师将直觉的错误——有趣的跳跃——同愚蠢或无知的错误区别开来,同时要求教师能适时地对运用直觉思维的学生予以赞同或予以纠正.”
例4甲有n+2枚硬币,乙有n枚硬币,双方投掷之后进行比较,求甲掷出的正面数比乙掷出的正面数多的概率.
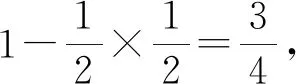
将甲、乙各投掷n枚硬币时,两人所掷出正面数甲=乙、甲>乙、甲<乙分别记为事件B、C、D,则P(B)+P(C)+P(D)=1,由对称性知,P(C)=P(D).则由全概率公式知,“事件A:甲、乙分别投掷n+2、n枚硬币时,两人掷出正面数甲>乙”发生的概率为
P(A)=P(B)P(A|B)+P(C)P(A|C)+P(D)P(A|D)

注意到A|D只有在“事件E:甲、乙各投掷n枚硬币时甲掷出正面数比乙掷出正面数恰好少一枚”发生的前提下,且甲剩下的2枚硬币都掷出正面时才可以发生,故
P(D)P(A|D)
=P(E)P(A|E) 则 P(A)=P(B)P(A|B)+P(C)P(A|C)+P(E)P(A|E) 另外,类似于例1,直接从数学运算的视角也可得到以下解法. 记“甲掷n+2枚硬币,有k枚硬币正面朝上”为事件Ak(k=0,1,2,…,n+2),“乙掷n枚硬币,至多有s枚硬币正面朝上”为事件Bs(s=0,1,2,…,n),“甲掷出的正面数比乙掷出的正面数多”为事件C,易知事件Ak,Bs相互独立,则 C=(A1B0)∪(A2B1)∪…∪(AkBk-1)∪…∪(AnBn-1)∪(An+1Bn)∪(An+2Bn), 且事件A1B0,A2B1,…,AkBk-1,…,AnBn-1,An+1Bn,An+2Bn之间彼此互斥. 由相互独立事件的概率乘法公式知, P(AkBk-1)=P(Ak)P(Bk-1) k=1,2,…,n+1, P(An+2Bn)=P(An+2)P(Bn) 由互斥事件的概率加法公式知, P[(A1B0)∪(A2B1)∪…∪(AkBk-1)∪…∪(An+1Bn)] =P(A1B0)+P(A2B1)+…P(AkBk-1)+…+P(An+1Bn) 类似于例1利用倒序相加法可得, 则 P[(A1B0)∪(A2B1)∪…∪(AkBk-1)∪…∪(An+1Bn)] 注意到 =2n(2n+2-2), 所以,甲掷出的正面数比乙掷出的正面数多的概率为 P[(A1B0)∪(A2B1)∪…∪(AkBk-1)∪…∪(An+1Bn)∪(An+2Bn)] =P[(A1B0)∪(A2B1)∪…∪(AkBk-1)∪…∪(An+1Bn)]+P(An+2Bn) 可见,逻辑推理和数学运算的详细过程都确切地驳斥了直觉感知所得的结果.因此直觉感知是逻辑推理和数学运算的先导,逻辑推理和数学运算是直觉感知的护栏.直觉感知不仅先于逻辑推理和数学运算,而且为它们提供目标与方向,策略与方法.但是,直觉感知不能保证严格性,甚或不能保证正确性,这就需要逻辑推理和数学运算的保驾护航以确定直觉感知的可靠性.其实,直觉感知看似是未经充分逻辑推理和数学运算的感性认识,但它不是凭空产生的,而是建立在经验的基础上,是经验积累和优化到一定程度后的顿悟,很多看似自发产生的直觉感知都是长期有意识地思考与探索的间接结果,即使所得答案是错误的也非常值得深入思考与探究. 前苏联著名物理学家福克曾指出:“伟大的及不仅是伟大的发现,都不是按逻辑的法则发现的,而都是猜测得来的;换句话说,大都是凭创造性的直觉得来的.”数学大师庞加莱也曾说过:“人们证明是用逻辑,而发明是用直觉……逻辑告诉我们走如此这般道路保证可以走得通,但是它没有具体指出哪一条道路通向目标不会出现障碍.为此,我们必须从远处眺望目标,而教导我们眺望的官能是直觉.没有它,几何学家就会像只会按语法作诗的作家一样毫无思想.”数学育人的基本途径是对学生进行系统的(逻辑)思维训练,训练的基本载体是逻辑推理和数学运算.”张景中院士曾指出:“推理是抽象的计算,计算是具体的推理,计算和推理是相通的.”《普通高中数学课程标准》(2017年版2020年修订)也指出:“数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.这些数学学科核心素养既相互独立、又相互交融,是一个有机的整体,是数学课程目标的集中体现.” 因此,概率教学中既要追寻直觉感知背后的逻辑推理与数学运算,也要感悟引领逻辑推理与数学运算前面的直觉感知,以期在直觉感知、逻辑推理与数学运算的交相辉映中促进学生思维的提升与发展.但直觉感知所得的结果不一定严谨或者正确,这个时候就需要按照一定的原理或公式进行逻辑推理或数学运算,以断定直觉感知的正确与否.当然,也存在先由数学运算获得结果,后进一步去寻找结果前面的直觉感知,并设法给出逻辑推理.或者是数学运算压根儿就难以施展或奏效,这时更应该在直觉感知和逻辑推理上多下功夫以寻求突破.正如史宁中教授所指出的:“学习数学的要义不仅仅是为了‘记住’一些东西,甚至不仅仅是为了掌握一些‘会计算’‘会证明’的技巧,而是能够‘感悟’数学所要研究问题的本质,‘理解’命题之间的逻辑关系,在‘感悟’和‘理解’的基础上学会思考,最终形成数学的直觉和数学的思维,这也是数学课程标准中提出‘四基’,强调‘基本思想’和‘基本活动经验’的本意.”当然,教学中如何将直觉感知、逻辑推理与数学运算完美结合的策略、途径与方式等是值得我们不断进行探索的课题.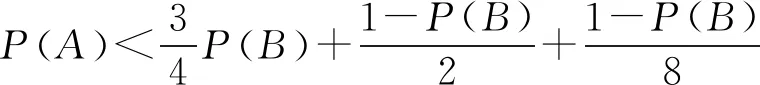
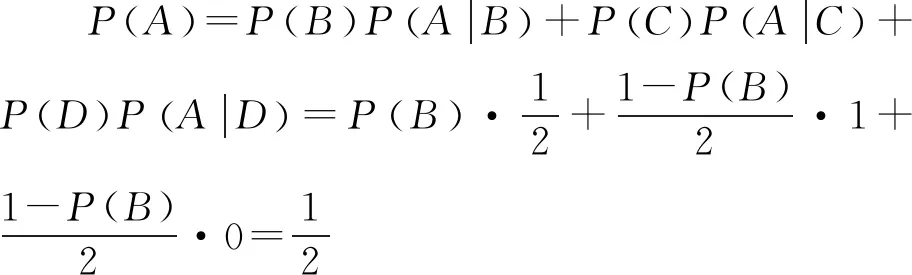
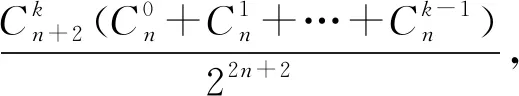
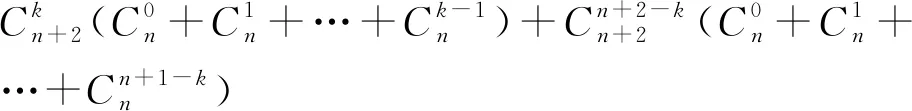
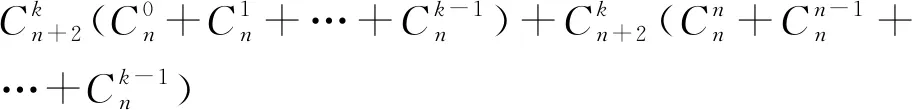
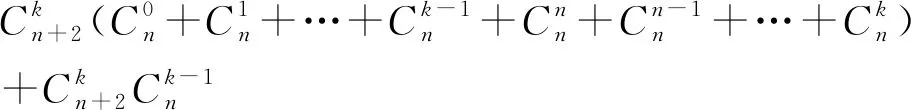
3 结语

