略论概率统计教材的整体把握

郑达艺

(福建教育学院数学研修部 350025)

比较人教A版《普通高中实验教科书·数学》(简称“旧教材”)与《普通高中教科书·数学》(简称“新教材”)中概率统计的内容[1,2,3,4],发现它们有以下几处不同:

(1)在古典概型部分,新教材引入“样本空间”概念,而旧教材没有这个概念.在旧教材中,需要应用样本空间概念时,采用举例说明的方式,如说明事件的关系与运算时,通过掷骰子试验给予说明.

(2)对于随机变量的概念,新教材的定义是:“一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X(ω)与之对应,我们称X为随机变量”;旧教材则先举掷骰子和掷硬币的例子,再定义“像这种随着试验结果变化而变化的变量称为随机变量”.

(3)对于二项分布的引入,旧教材通过介绍掷n次硬币的试验引入二项分布;而新教材先介绍n重伯努利试验,再进一步介绍二项分布.

(4)在统计学部分,旧教材主要介绍随机抽样和用样本估计总体,新教材先系统介绍数据整理和数据分析,再进一步介绍随机抽样和用样本估计总体;对于线性回归分析,旧教材直接给出线性回归方程及其计算,再给出残差分析,新教材先从散点图给出相关系数,再进一步给出线性回归方程及最小二乘法估计参数,最后给出残差分析.

从这些比较中可以发现,旧教材在概率与统计部分往往不追求概念的严格定义,有时对知识的引入也缺乏必要的铺垫,从而影响学生对知识的理解.新教材旨在使概率统计的知识系统化和加强知识的逻辑基础,以防止出现知识的碎片化,夯实知识的逻辑根基.以下我们从概率论和统计学两个方面出发,指出高中数学教师应具备的学科素养,以引导教师加强对教材的整体把握,加深对教材的深入理解,帮助教师做好高中概率统计的教学工作.

1 整体视野下高中教师必备的概率论学科素养

“概率”概念的引入,就是希望用数学方法度量和研究这些不确定的事物,即概率论就是用数学方法研究随机现象的一门学问[5],因此,整体上系统把握概率知识、理解处理随机现象问题的逻辑基础和会运用概率模型解决问题是高中数学教师必备的概率论方面的学科素养.

1.1 概率论知识的螺旋上升与系统化

(1)概率概念的螺旋上升与系统化

小学阶段,根据学生的思维品质和心理特征,从形象直观的角度引进概率,把对事件发生可能性大小的度量称作概率,这样定义能使学生形象地理解概率是什么,适合小学生的学习特点,但小学对概率的定义是定性的,而不是定量的,因而不利于概率的计算.因此初中阶段在小学的概率定义的基础上,进一步介绍频率与概率的关系,通过随机试验,总结归纳出概率是频率的稳定值.高中阶段,再次把随机事件的概率定义为频率的稳定值,且除了通过抛硬币试验进行说明外,同时还从伯努利大数定律角度进行说明.大学阶段,则借助测度论的理论,基于样本空间给出概率的公理化定义,定义概率是以随机事件为自变量且满足非负性、规范性、可列可加性的集函数.事实上,概率的频率定义和概率的公理化定义,两者具有连贯性及一致性,因为频率也具有非负性、规范性、有限可加性的性质;并且这两种定义本质上都是把概率看成是随机事件的固有属性,因此可以把公理化定义看成是频率定义的发展和完善,从概率定义出发借助演绎推理可得到概率论的所有数学化的结论.

(2)概率计算的螺旋上升与系统化

对于概率的计算问题,初中阶段主要采用列举法、列表法及树形图的方法求古典概型的概率.高中阶段面对更加复杂的随机现象,新教材引入样本空间的概念.引入样本空间的概念,其一是使得随机事件与样本点的集合(样本空间的子集)一一对应,通过类比集合之间的关系和运算得到随机事件的关系与运算,以此为基础给出概率的重要性质,为求复杂随机现象的随机事件的概率做准备;其二是通过样本空间的引入可以证明古典概型的计算公式,据此只要找出样本空间及所求随机事件对应的子集,概率便可以轻松求解出来,这是对初中列举法、列表法求古典概型概率方法的深化和升华.在此基础上,基于条件概率和乘法公式得出全概率公式和贝叶斯公式,对于分类情况的概率计算,全概率公式相对初中树形图方法更为方便、简洁、普遍.高中阶段的选择性必修进一步引进随机变量,通过随机变量的定义可把随机事件数量化,再根据随机变量取值特点将其分为离散型随机变量和非离散型随机变量(一般研究连续型随机变量).对于离散型随机变量,主要研究它们的常见概型及其分布列;对于连续型随机变量,主要研究它们的常见概型及其密度函数,还可以进一步利用微积分工具对它们的密度函数和分布函数进行研究.这也是对前面概率计算的进一步升华,例如把古典概型中的n重伯努利概型作为离散型的二项分布进行研究,把几何概型作为连续型的均匀分布进行研究.

1.2 把握处理随机现象问题的逻辑依据

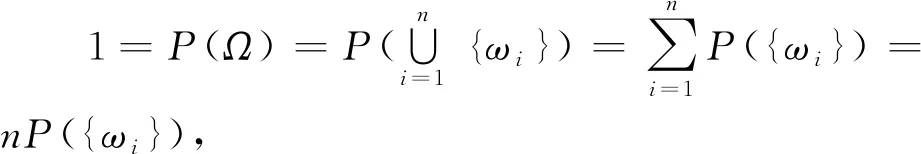
这样,对于古典概型的概率计算问题,根据古典概型的概率计算公式,由样本空间求随机事件的概率问题,就变成了严格的数学计算问题.以下我们看一个实例.

例1一个家庭中有两个小孩,已知其中一个是女孩,问另一个也是女孩的概率是多少?(假定生男生女是等可能的)

解根据题意,样本空间为

Ω={(男,男),(男,女),(女,男),(女,女)};

B表示事件“至少有一个是女孩”,

A表示事件“两个都是女孩”,则

B={(男,女),(女,男),(女,女)},

A={(女,女)}.

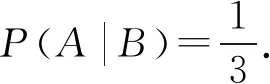
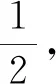
又如,在一些具体问题中能不能用频率替代概率进行计算,要看是否具备两个条件:第一,样本是否是简单随机抽样得到的(即样本是否能很好地代表总体);第二,样本容量是否足够大.因为如果是简单随机抽样,样本作为随机变量与总体有相同概率分布,再依据伯努利大数定律,如果样本容量足够大,那么就可用频率近似计算概率.再如新教材在引入二项分布时,先介绍满足n重伯努利概型的两个条件再介绍二项分布,那么在判断什么样的概型是二项分布时,我们就可以依据这两个条件是否满足判断是否是二项分布.以下我们看一个实例.

例2在400毫升的水中随机游动着200个菌团,从中任取1毫升水,求其中所含菌团的个数不少于3的概率.

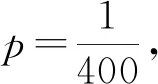
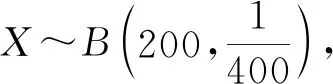
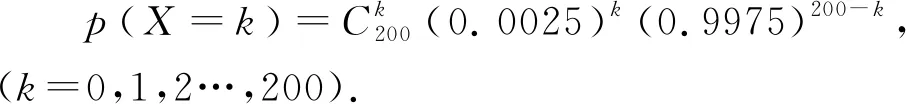
进一步得:p(X≥3)=1-p(X=0)-p(X=1)-p(X=2)=0.0144.

通过该例题的解题分析,我们可以发现解题过程与数学确定性现象解题是一样的,也就是根据已知条件,分析是否满足概型的基本条件,只要满足了二项分布的条件,就可以根据二项分布进行计算.因此,如果教师能深刻理解概率论问题的逻辑基础,那么对随机现象问题的处理就再也不是难题.

1.3 善于运用概率模型解决实际问题

新教材引入随机变量后,使概率论从事件及其概率的研究扩大到随机变量及其概率分布的研究.根据随机变量取值的特点,随机变量分为离散型随机变量和非离散型随机变量(一般研究连续型).对于离散型随机变量,我们研究它们的常见模型及其分布列;对于连续型随机变量,我们研究它们的常见模型及其密度函数.在解决实际问题时,我们先对客观问题进行抽象,再根据随机变量服从的常见概率模型的条件判断所服从的模型,根据服从的概率模型解决问题.例如上面的例2就是运用离散型的二项分布概率模型来解决问题,这也是新课标要求的“掌握运用概率模型解决问题”的具体体现.

在利用古典概型求随机事件的概率时,也可运用模型解决问题.例如,对于古典概型的分房问题:设有n个人,随机地住进N个房间中的任意一间(n≤N),且设每个房间可容纳的人数不限,试求下列各事件的概率:(1){某指定的n个房间中各住一人};(2){恰好有n个房间,其中各住一人};(3){某指定的一房间中,恰有k个人}.很多实际问题就可以运用分房问题概型进行解决,例如:某班有n个学生,试求该班至少有两名学生的生日相同的概率.我们可以通过求该事件的对立事件的概率进而求该事件的概率,它的对立事件的概率即为n个学生生日各不相同的概率.如果我们把一年的365天看成365个房间,n个学生生日各不相同的概率即为n个人每人各住一间的概率,这样该问题就转化为了分房问题的第二小问的问题.

2 整体视野下高中教师必备的统计学学科素养

统计学的主要研究内容是建立在数据基础上通过数据进行推断,因此,数据分析和统计推断是统计学两大教学内容,而进行统计推断的样本数据是随机的,也因此理解统计推断必须基于概率论的基础之上.

统计学部分主要介绍两个问题:一是对所给数据的整理分析;二是通过样本推断总体的思想.小学阶段主要让学生学会对数据进行整理,例如由所给的数据,让学生画直方图(条形图)、折线图及扇形图,以了解研究对象数量情况、数量变化情况及对象所占比例.初中阶段,在小学所学基础上进一步学会分析数据,例如通过找出所给数据的中位数、众数,以及计算它们的平均数、极差、方差等,以了解数据集中趋势以及离散程度.同时,还简单介绍了通过样本估计总体的思想.在小学和初中的基础上,新教材高中必修第二册系统介绍了数据收集(即怎么抽样)、 数据整理(即求样本的数字特征以及数据的直观表示)、数据分析,同时也介绍了统计学的重要思想方法:用样本估计总体(用样本的数字特征估计总体的数字特征、用样本的分布来估计总体的分布等).选择性必修的统计学部分主要介绍成对数据的统计相关性、一元线性回归模型及其应用、列联表与独立性检验.在这里进一步贯彻统计学通过样本估计总体的思想方法,例如通过建立样本的经验回归模型预测总体的响应变量,使统计学从描述时代进入推断时代;通过独立性检验介绍了假设检验的思想方法,这是在假设零假设正确情况下构造样本函数,在已知所构造样本函数分布情况下找出小概率事件,再根据样本数据判断小概率事件是否发生,进而判断是接受零假设还是否定零假设.

从高中统计学的内容看,必修部分主要介绍的是数据的收集、整理分析,这部分内容相对容易.选择性必修部分才是统计学教学重点和难点,这部分内容是基于样本数据进行统计推断,而样本数据是随机的,因此理解统计推断必须基于概率论的基础[6].下面对怎样以概率论为基础理解一元线性回归模型和独立性检验的统计推断谈点想法.

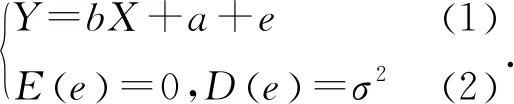
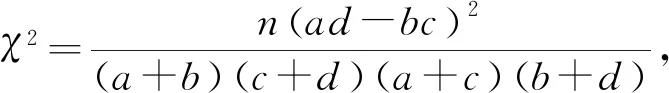
总之,只有从整体上认识和把握教材,对概率统计知识形成系统化认识,深刻理解概率统计知识的逻辑基础,才能真正做好高中概率统计的教学工作.