高中数学教学境界跃升的“三步曲”
陈重阳
(浙江省温州中学 325000)
中国禅语说,认识世界有三重境界:看山只是山,看山不是山,看山还是山.这三重境界反映了人们对事物认识逐步深刻、逐渐提升的发展过程.类比数学教育,高中数学教学也有这三重境界,这三重境界是一名优秀教师必经炼“技”、达“术”、悟“道”三个阶段,是教学境界跃升的“三步曲”.研究者根据自身的教育教学经验,结合自己在温州市高三数学研讨会上的一节公开课——“直线与抛物线的位置关系”三次教学设计粗谈一些认识.
1 看山只是山——数学教学的炼“技”境界
看山只是山,是数学教学的初级阶段,简单理解就是“新”“初”“雏”. 这个阶段看问题往往是孤立的,一切数学和教学在教师眼里都是其本原的状态,较少用联系的观点看问题,常常停留在经验上.“直线与抛物线的位置关系”的初期教学设计就是这样的表现,单纯关注直线与抛物线的位置关系,没有确立直线与曲线位置的全局观念,更没有解析几何学科的一般性方法和思想.
第1次教学设计简述
师:直线与抛物线有哪些位置关系?
生(预设):相离、相切、相交.
问题1直线l过点P(1,0),与抛物线C:y=x2恰好有一个公共点,求直线l的方程.
预设:这个问题中,学生容易忽略斜率不存在时,直线l的方程x=1.
问题2直线l过点P(1,0),与抛物线C:y=x2相交于两点A(x1,y1),B(x2,y2).
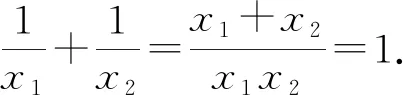
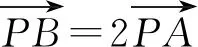
(学生只用直线方程的“线解析”(斜率为参数)来求解,没有体验与 “点解析”(点坐标为参数)的异同比较.)
问题3P是直线y=x-1上的动点,过P引抛物线C:y=x2的两条切线,切点分别为A(x1,y1),B(x2,y2).(1)探索直线AB是否过定点;(2)求△PAB面积的最小值;(3)证明:∠PFA=∠PFB(其中F是抛物线焦点);从上述结论中至少选择一个解决.

第1次教学设计以知识为主线设置了三个问题,教学意图指向直线与抛物线的位置判断、相交问题、相切问题,问题之间思维切换相对孤立,缺乏解决问题的方法引导.教学方式以传统的单向传授为主,过于重视教师的主导地位,课堂模式不够开放,过重耽于对细碎课堂教学技巧的痴迷,缺乏对数学教学独特理解和个性张扬.究其因,还是未能跨越出“技”的境界.
用正确的方法去做一件事情是为“技”.遵循数学教育教学规律上好一堂课属于教学之“技”.看山只是山,处在数学教学的炼“技”境界,系回答“是什么”的阶段,乃微观研究.“技”是教师课堂教学技能(诸如课堂语言、板书、节奏等)外在表现和数学专业素养(诸如数学理解、教材处理、教学设计等)内在表现的初步综合,需要在课堂实践中不断磨炼.
随着教育观念的转变、教材体系的更新、教育对象的变化,“技”的作用将越来越暴露其局限性,往往让数学教学困于“只见树木不见森林”的窘境.这时,不仅需要不断内蕴的反思与学习,夯实数学专业的“底子”,拓展教学素养的“里子”,而且还需要反复外向的实践锤炼,积淀教学经验.
2 看山不是山——数学教学的达“术” 境界
看山不是山,是数学教学的中乘境界,简单理解就是“会”“融”“通”.这个阶段看事物不再是单纯孤立的,而是运用联系的观点看待问题、分析问题,看问题的角度也是多方位、多层面的.对教师而言,不仅要理解数学、理解教材、理解学生,而且要研究数学的教育教学规律,并在教学实践中不断创造适合不同教育对象的独特方法,自觉地把教学实践经验向理论的高度提升.在第1次教学反思的基础上,这次教学设计已站在学科的一般性思想方法的高度上,问题注重开放设计,实施探究式教学.
第2次教学设计简述
师:这节课,我们通过“直线与抛物线的位置关系”的复习,一起来感悟用代数的方法解决几何问题的思想魅力.
问题1直线l:y=ax+b和抛物线C:y=x2,请你具体给出a,b的一组值,使直线l和抛物线C相交.
预设:在学生思考与讨论后追问: 直线l和抛物线C相交,a,b需满足什么条件?
(相交时,联立直线与抛物线方程得Δ=a2+4b>0.)
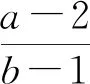
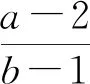
问题2已知a+b=0,直线l:y=ax+b和抛物线C:y=x2相交于两点A,B,________(请你添加条件),求直线l的方程.
预设:学生从线段的长度、点的位置、夹角、面积等角度提出多种方案.例如:
生1:b=1;
生2:|AB|=2;
生3:A,B的中点在y轴上;
生4:∠AOB=90°;
生5:S△AOB=1;

生7:直线l与椭圆4x2+y2=1相切;
……
授生以鱼,不如授生以渔.问题1可以通过“形”或“数”多种方式确定直线与抛物线相交位置,打开了学生的思维“脚镣”,有效地引导学生开展数学学习的思维活动.尤其是问题2的开放性设计,培养学生学会思考、学会提出问题、解决问题的数学习惯,构建了“形散神不散”的教学模式,是达“术”的表现.但是,在试课之后,感觉对学生来说问题2的解决方法还是比较单一,课堂还缺少“一叶知秋”“一课一世界”的教学意境.这就要求教师对数学、教学、教育有更深的理解,需要追求更加高远的教学立意.
知道事物的原理是为“术”.如果说上好一堂课属于“技”,那么懂得怎样上课属于“术”.看山不是山,处在数学教学的达“术”境界,是回答“为什么”的阶段,乃中观研究.此境界,不满足于“技”的细碎、凌乱,已趋于在教学意识、教学思想上的探索,且教学技艺在量上的积累有相当部分产生质的飞跃,开始用心去思考数学和教学,思考也多了一些理性和深度,但还缺少一种“一叶一菩提,一花一世界”的教学立意.或者说,已经从森林中走出,对森林的草木都有了相当精确的认知,也知道森林在山中,却还停留在对山的仰视,“只缘身在此山中”,故尚不能窥知山的全貌,还需要迈向更高境界.
3 看山还是山——数学教学的悟“道”境界
看山还是山,是数学教学的上乘境界,简单的理解就是“明”“透”“悟”.这个阶段,我看山是我要的山,我看水是我要的水,是一种洞察事物的本质,探寻事物规律的升华过程.教学立意追求大“道”至简,教学设计蕴含“一叶一菩提,一课一世界”的教学意境.在前两次磨课之后,教学思想也有了升华,进而提出本节课的立意:解析几何问题的“立”与“破”——对一道高考题的改创与探究.立,借助几何直观提出问题.破,选择代数语言理性解析.
第3次教学设计简述
师:给定一条直线和曲线,我们会研究哪些问题?又是如何研究的?这节课就以一道高考题为例,从直线与抛物线的位置关系中发现解析几何的“秘密”.
问题情境(2009年北京高考题改创)已知点P和曲线C:y=x2,若曲线C上存在一点A,使得线段PA的中点也在曲线C上,则称点P为“好点”,点A为“伴点”.
问题1判断点P(1,0)是否为“好点”,对应的“伴点”有几个?
(学生容易从几何直观得出肯定答案,但还需进一步严密论证.)
问题2请再给一些“好点”,并尝试描出“好点”所在的平面区域;
(借助几何直观提出问题,选择恰当的代数语言理性解析,体会解析几何问题中的“立”与“破”.)
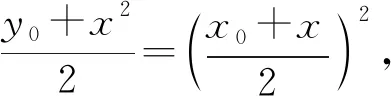
变式1请你具体给出a,b的一组值,使直线l:y=ax+b上所有点都是“好点”;
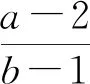
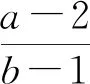
问题3已知一个“好点”对应两个“伴点”,若“好点”P的两个“伴点” 是A1,A2,以此几何图形为背景,(请你添加条件),设计一些题目,并说说解决它的方法和过程.
(开放思维空间,拓宽问题广度,加深理解解析几何问题的“立”与“破”,培养学生提出问题、解决问题的能力.)
预设:不同层次的学生都能在这个问题上有不同层次的答案,例如,
生1:若A1A2的中点为M,求证:PM⊥x轴;
生2:当P(1,0)时,求“伴点”A1,A2的坐标;
生3:当P满足什么条件时,PA1⊥PA2?
生4:当P在直线l:y=x-1上运动时,求△PA1A2面积的最小值;
……
问题1中,学生容易借助几何直观提出猜想,体现数学的哲学观点,数学是发现也是发明的,数学的发现往往依赖于几何的直观和思维的直觉.但是,类似问题1的直观猜想还需代数语言理性解析,自然转到问题2的“线解析”和“点解析”的方法及异同比较,让学生感悟解析几何的学科精髓.问题2的两个变式貌似研究“好点”问题,实质是直线与抛物线的位置关系,避免了看山只是山的狭隘,逐渐从看山不是山到看山还是山的转变.所有问题均蕴含倚“形”(几何直观)立问,靠“数”(代数推理)破解的思想,凸显学科本质;尤其是问题3的开放性教学,享受“问题自由”,更是体现本节课“立”与“破”的教学立意,彰显“本来无一物,何处惹尘埃”的潇洒和大气,是“技”熟、“术”达之后,心领神会数学本质和教学规律,是悟“道”的表现.
洞明事物的本质和规律是为“道”.通透数学本质和教学规律,“技”“术”精通之上的教育抽象而升化为数学教学之“道”.看山还是山,处在数学教学的悟“道”境界.“道”的境界,不仅懂得“是什么”和“为什么”,而且还要知道“怎么做”,最关键的还是要悟出“怎么来的”,乃宏观之旨归.此境界,是以探寻教学的规律为目标的归纳、概括,是确立说法的过程,不满足于精熟的教学技艺,更不停留在“进乎技矣”的“术”的层次上,有胆量走出“庐山”,以更广阔的视野看数学的教育教学,从“入乎其内”,到“超乎其外”,既能“观之”又能“写之”.或者说,对“道”的追求,目的就在于把“技”“术”的经验积累上升到理性认识的高度,通俗地说就是朝着教育名家的方向迈进.
具体来说,从教师教学角度看,“技”“术”“道”分别对应“上好一堂课”“懂得怎样上课”“成为教育行家”三个阶段.从数学课程标准的视角来看[1],“技”“术”“道”分别属于教育学生如何进行“分析问题,解决问题”“提出问题,解决问题”“发现问题,享受问题”的三个层次.当然,“技”“术”“道”并非截然分开的三个不相关的部分,三者之间较低的层次中可能包含了较高层次的成分,只是还处在不自觉状态.超越“技”和“术”,而趋于“道”境,将“道”的体悟作为远期旨归,无疑是教学境界的最高目标,自然要付出更多的努力.
4 结语
“看山只是山”是建构,“看山不是山”是解构,“看山又是山”是重构,这三重境界,是教学智慧和思想走向成熟的一个必然过程.静止看,三重境界是递升的;动态看,不是以“悟道”为目标,“技”“术”再精深,也是欠高的境界.如何做到“技”精、“术”深、“道”高,完全取决于自己的眼光、毅力和追求,需要在教学实践中不断积淀磨炼.人生如此,教学亦如此.

