无人车辆行驶路径的分层协调最优跟踪控制

包套图，曾 岑

（1.渤海船舶职业学院，辽宁 葫芦岛 125000；2.大连理工大学，辽宁 大连 116024）

1 引言

汽车保有量的提高严重增加了交通拥堵和交通事故的概率，自动驾驶技术的提出在一定程度上解决了由于饮酒、疲劳等人为因素导致的事故［1］。车辆运动控制是自动驾驶的关键与末端技术，是自动驾驶的主体行为［2］。因此，研究车辆运动控制技术对促进自动驾驶技术的成熟和落地具有重要意义。

车辆跟踪控制一般解耦为纵向控制和横向控制问题，纵向控制用于消除纵向的速度偏差，横向控制用于消除车辆质心与期望轨迹点的位置偏差［3］。横向控制是车辆跟踪控制的核心问题，分为无预瞄控制和预瞄控制两个大方面。无预瞄控制中Stanley方法［4］最为经典，它以前轴中心与参考轨迹最短距离为参考，计算前轮转角。但是由于轮胎侧偏的存在，使得横向控制与横向位移存在延迟，这种延迟在车速较高时会引起控制波动和驾驶轨迹振荡。预瞄控制分为单点预瞄和多点预瞄两种情况［5］，单点预瞄在路径前方选择一个预瞄点，绘制一条当前位置与预瞄点相切的轨迹并跟踪。文献［6］以加权方式将无预瞄和单点预瞄控制方法结合，实现了车辆在不同工况下的路径跟踪。多点预瞄是指在路径点上选择多个参考点，通过加权将各点横向偏差进行综合的方法，常用的多点预瞄方法包括线性二次规划和模型预测控制等。文献［7］以自动清扫车为研究对象，基于多点预瞄方法对车辆运动进行控制，经实验验证该方法能够满足清扫车辆控制精度需要。上述方法能够得到较为精确的路径跟踪控制结果，但是控制过程中没有关注能耗、终点控制精度等因素，因此有必要进行进一步研究。

针对智能车辆的路径跟踪控制问题，建立了车辆的动力学模型和单点预瞄控制系统模型，设计了分层协调最优控制的路径跟踪方法，其中上层控制器基于系统状态求出最优控制律，下层控制器实现对最优控制律的准确跟踪，最终实现了车辆在不同工况下对路径高精度、低能耗的跟踪控制。

2 车辆跟踪系统建模

2.1 汽车动力学建模

为了建立车辆的动力学模型，首先作以下4点假设：

（1）忽略车辆的俯仰和滚动运动；

（2）车辆前轮负责转向，后轮没有转向能力；

（3）忽略车辆行驶过程中的空气组合和坡道阻力；

（4）左右车轮均工作在线性区域，且特性相同。

在以上4点假设的前提下，车辆可以被简化为具有3个自由度的单轨模型，如图1所示。

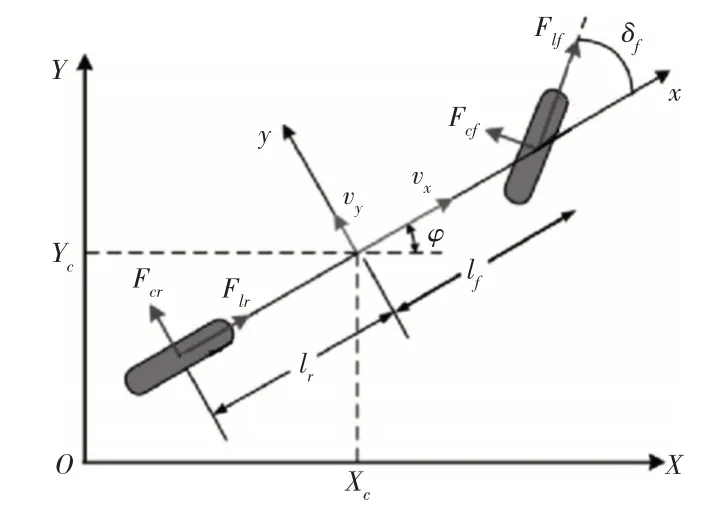
图1 车辆简化模型Fig.1 Simplified Vehicle Model

图中：OXY—道路坐标系；（Xc，Yc）—车辆质心在道路坐标系的坐标；oxyz—车辆坐标系；x轴—车辆纵向前进方向；z轴—天向；y轴—按右手准则确定的方向；vx—车辆纵向速度；vy—车辆横向速度；lf—车辆前轴距；lr—车辆后轴距；δf—前轮转角；φ—车辆横摆角。根据力平衡公式和力矩平衡公式，得到车辆动力学模型为：

式中：m—车辆质量；ax—车辆纵向加速度；Cαf、Cαr—前后轮侧偏刚度；Iz—车辆绕Z轴的转动惯量。

2.2 预瞄模型距离设定

与非预瞄控制比，预瞄控制具有鲁棒性好、控制精度高等优点［8］，因此这里使用单点预瞄控制方式。单点预瞄控制模型，如图2所示。

图2 预瞄跟踪控制模型Fig.2 Preview Tracking Control Model

图中：L—预瞄距离；ye—横向距离误差；εe—方向误差。

预瞄距离的设定对路径跟踪控制效果的影响具有一定规律性：当预瞄距离较大时，路径跟踪系统的稳定性较好；当预瞄距离较小时，路径跟踪精度较高。为了兼顾系统的稳定性和跟踪精确性，经过不断实验和调整，将预瞄距离设置为横向速度的分段函数，为：

2.3 预瞄模型及线性化

根据图2所示的单点预瞄跟踪控制示意图，得到单预瞄点的跟踪模型为：

式中：ωr—车辆横摆角速度；KL—对应于预瞄点的转换系数。

结合式（1）和式（3），选择路径跟踪控制系统的状态量为X={φ，vx，vy，ye，εe}，控制量u={ax，δf}，可以得到系统状态空间方程为：

由式（4）表达式可知，路径跟踪系统的状态空间方程为非线性形式。在(X0(t)，u0(t))位置进行泰勒展开，得：

式中：A—系统矩阵；B—控制矩阵，且有：

3 分层协调最优控制器设计

3.1 最优控制器结构

这里的控制目标关注控制精度和能量消耗两个方面，为了实现此控制目标，设计了分层协调最优控制器，包括上层控制器和下层控制器两个控制器，如图3所示。

图3 最优控制器结构Fig.3 Structure of Optimal Controller

图3 中虚线框内为分层协调最优控制器，上层控制器使用LQR最优控制方法，得到控制精度、能量消耗综合最优意义下的控制量uop={ }arop，δfop。下层控制使用参数智能整定PID控制器，以刹车气动压力Pb、油门节气门开度αth为控制量，实现车辆对最优控制量uop={arop，δfop}的精确跟踪。

3.2 LQR最优控制器设计

按照LQR最优控制器设计原理，目标函数应包括终端误差、过程累积误差、控制量约束等方面。但是考虑到路径跟踪控制过程可以视为无限时间的线性二次型系统，因此目标函数设计为［9］：

式中：J—目标函数；X—状态量；U—控制量；t0—时间起点；Q—状态量加权矩阵；R—控制量加权矩阵。

当权值矩阵Q、R为单位对角阵时，各状态量和控制量的重视程度一致。但是在车辆行驶过程中，当车速较小时，车辆操纵稳定性较好，此时应更加关注车辆对给定路径的跟踪精度；当车速较大时，车辆操纵稳定性变差，此时应降低对跟踪精度的关注，适当降低车速而提高车辆操作稳定性和行驶安全性。基于上述考虑，将权值矩阵Q、R设置为车速v的函数，为：

3.3 参数智能整定PID控制器

对于下层控制器，使用参数智能整定PID控制器进行设计。基于LQR得到的最优控制量arop，得到车辆的纵向控制逻辑，如图4所示。将车辆实际加速度计为ar，设计一个变量a͂r=ar-arop，当a͂r≤0即实际加速度小于最优加速度时，则使用发动机提供动力，进一步增大加速度；当a͂r＞0即实际加速度大于最优加速度时，则使用制动器提供阻力，从而减小加速度。

图4 纵向控制逻辑Fig.4 Vertical Control Logic

使用参数智能整定PID控制器，基于变量a͂r得到发动机节气门开度αth或刹车气动压力Pb。由于两个PID控制器的设计原理完全一致，因此以参数智能整定PID控制器1为例对控制器设计原理进行介绍。参数智能整定PID控制器原理，如图5所示。

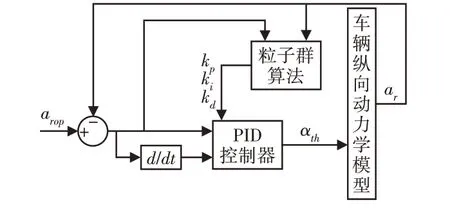
图5 参数智能整定PID控制器Fig.5 Parameters Intelligence Calibration PID Controller

基于PID控制的节气门开度αth计算方法为［10］：

式中：αth(t)—t时刻的节气门开度；kp—比例系数；ki—积分系数；kd—微分系数。

传统PID控制器使用固定的比例系数、积分系数、微分系数，但是控制对象状态和工况是实时变化的，固定的PID参数难以对被控对象具有实时适应性。为了解决这一问题，这里使用粒子群算法实时整定PID参数。粒子群算法原理较为简单，这里不再介绍，仅对粒子编码方式和优化目标函数进行明确。粒子使用十进制3维度编码方式，即粒子编码为(kp，ki，kd)。优化的目标函数设置为：

式中：f—目标函数；j—时刻；t—当前时刻。式（9）表示优化的目标为车辆实际加速度与最优加速度的累积误差最小。按照上述设置方法，可以得到具有实时适应性的PID控制器参数kp，ki，kd。

4 路径跟踪验证与分析

4.1 车辆参数设置

为了验证分层协调最优控制器的路径跟踪控制性能，在Carsim环境中建立车辆模型，并基于Matlab搭建控制器模型，车辆参数，如表1所示。

表1 车辆参数Tab.1 Vehicle Parameters

车辆常用行驶工况为变道-直线行驶、小曲率转弯、大曲率转弯等工况，因此这里通过这3个工况对控制器进行验证。

4.2 变道-直线跟踪

给定一个直线路径，如图6所示。图中实线为道路边界线，虚线为道路中心线，该道路为同向双车道路径。黑色矩形表示行驶车辆，车辆行驶过程中发现前方障碍物，规划并跟踪避障路径，避障路径按照文献［11］方法规划得到，图6中细实线为避障路径，实心点为避障路径结束点，避障结束后沿直线行驶。

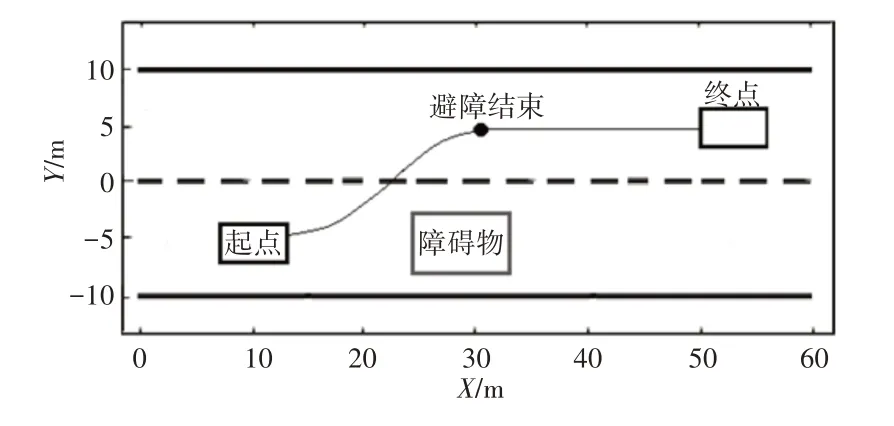
图6 变道-直线路径Fig.6 Lane Change-Straight Path

分别使用这里分层协调最优控制器（控制器1）、LQR最优控制+传统PID控制（控制器2）、文献［12］的优化控制方法（控制器3）进行路径跟踪，统计3种控制器的最大横向偏差，结果如下：控制器1跟踪的最大横向偏差为0.027m，控制器2跟踪的最大横向偏差为0.036m，控制器3跟踪的最大横向偏差为0.033m。

跟踪误差表明：控制器1、控制器2、控制器3在变道-直线行驶工况中，都能够对给定路径进行跟踪。从跟踪精度看，控制器1的跟踪精度高于控制器2 和控制器3，这是因为控制器1 中的LQR最优控制综合考虑了控制精度和控制耗能，反应在控制过程中，表现为控制精度更高、控制量幅值更小，因此控制器1的控制精度整体优于控制器2和控制器3。

4.3 小曲率转弯

给定一个U形轨迹，如图7所示。图中虚线为轨道的中心线，为本节跟踪的路径；虚线两侧的实线为道路边界线。

图7 U形路径Fig.7 U-Shaped Path

分别使用控制器1、控制器2、控制器3进行路径跟踪，其中控制器1和控制器2得到的最优控制律一致，3种控制器得到的控制量，如图8所示。

图8 不同控制方法的控制量Fig.8 Control Quantity of Different Control Method

图8（a）中，纵坐标数值为正时表示发动机节气门开度，数值为负时表示刹车气动压力。

由图8可以看出，这里分层协调最优控制器得到的控制量在幅值上整体小于控制器3，这是因为使用LQR最优控制方法计算控制律时，平衡了控制精度和控制量能耗，因此控制律在整体幅值上小于控制器3的优化控制方法。

统计控制器1、控制器2和控制器3对给定路径跟踪的最大横向偏差和最大方向偏差结果，如表2所示。

表2 最大偏差Tab.2 Maximum Error

由表2种数据可知，控制器1的最大横向误差和最大方向误差最小，表示控制器1的跟踪控制精度最高，控制器3的跟踪控制精度次之，控制器2的跟踪控制精度最差。这是因为，控制器1和控制器2相比，控制器2使用传统PID控制，控制器1使用的是参数智能整定PID控制，参数智能整定PID控制能够根据系统状态实时调节PID参数，使PID控制器对系统状态和工况具有实时适应性，因此控制器1比控制器2的精度高。

综合控制器1和控制器3，控制器1的控制精度好于控制器3，且控制律幅值也整体小于控制器3，这是因为控制器1 中的LQR最优控制综合考虑了控制精度和控制耗能，反应在控制过程中，表现为控制精度更高、控制量幅值更小，因此控制器1的控制精度和幅值整体优于控制器3。

4.4 大曲率转弯

为了验证分层协调最优控制器的鲁棒性，设计一个具有连续转弯、大曲率的复杂道路工况，如图9所示。图中实线为道路边界线，虚线为道路中心线，为这里需要跟踪的路径。图中矩形位置为路径起点，箭头方向为机器人前进方向。

图9 复杂道路工况Fig.9 Complex Road Conditions

分别使用控制器1和控制器3对复杂道路进行跟踪，其中控制器1能够实现对给定复杂路径的跟踪，而控制器3在第1个大曲率转弯时对路径跟踪失败，控制器1和控制器3的复杂路径跟踪结果，如图10所示。图10（a）中道路中心虚线为待跟踪路径，蓝色实线为控制器1的实际跟踪结果；图10（b）中粗实线为控制器3的跟踪结果。

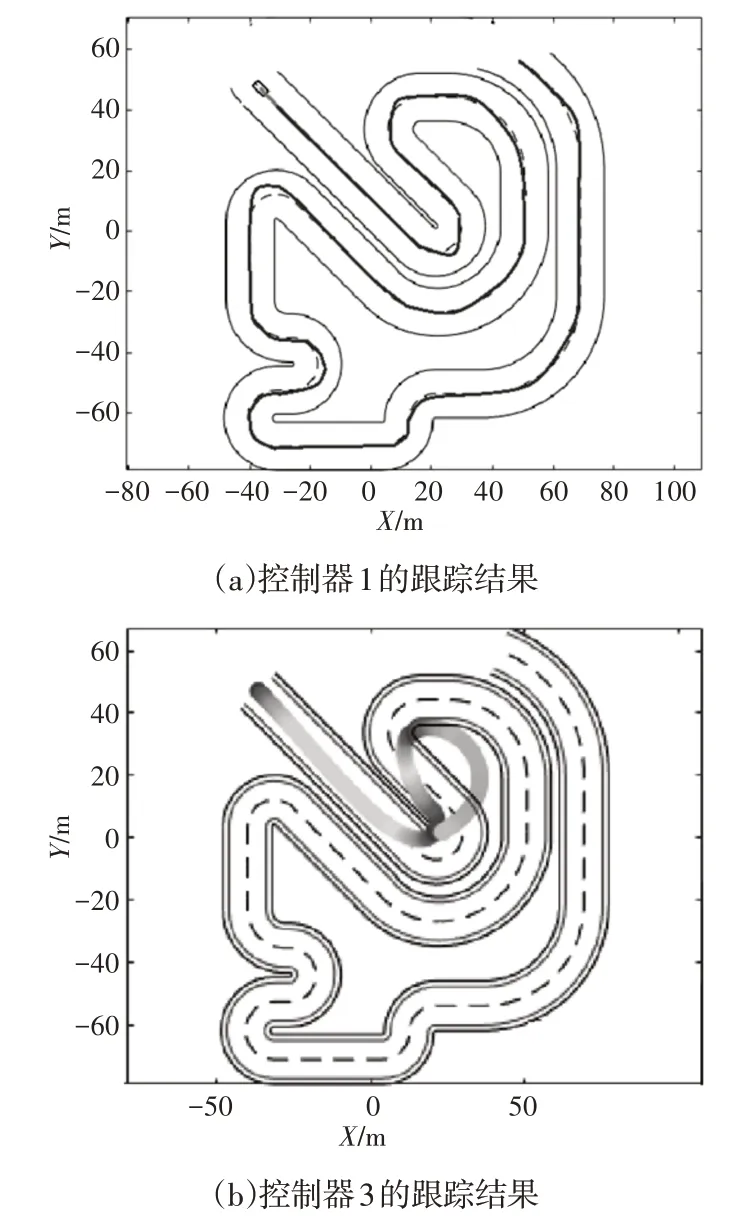
图10 两种控制器的跟踪结果Fig.10 Tracking Result of the Two Controllers

由图10可以明显看出，控制器1实现了对连续转弯、大曲率等复杂道路的精确跟踪，在道路转弯处的跟踪误差略大于直线位置。控制器3在第1个大曲率转弯位置，实际跟踪路径就超出了道路边界，说明无法实现对大曲率转弯路径的跟踪。经统计，控制器1对复杂路径跟踪的最大横向偏差为0.103m、最大方向偏差为1.987°，实验数据和实验结果表明，控制器1对复杂道路也具有较强的高精度跟踪能力，即分层协调最优控制器具有较强的跟踪能力和较好的鲁棒性。

5 结论

这里研究了无人车辆行驶路径跟踪控制问题，建立了车辆动力学模型和单点预瞄控制系统状态空间方程，设计了分层协调最优控制器用于路径跟踪。经实验验证得出以下结论：（1）在变道跟踪直线路径和U型路径转弯中，分层协调最优控制器、LQR最优控制+传统PID控制、文献［12］优化控制都能够实现路径跟踪；但是分层协调最优控制器的跟踪精度优于LQR最优控制+传统PID控制、文献［12］优化控制；（2）对于具有连续转弯、大曲率的复杂道路，分层协调最优控制器实现了精度较高的路径跟踪控制，文献［12］的优化控制无法跟踪上述复杂道路工况；（3）从变道跟踪、U形转弯和大曲率连续转弯等工况可以看出，分层协调最优控制器具有较强的跟踪能力和较好的鲁棒性。