融合应变响应的结构载荷/参数联合识别的EGDF法

万志敏，王 婷，曹 健，邵仁玉

（南通职业大学汽车与交通工程学院，江苏 南通 226007）

1 引言

结构上的外载荷［1-4］对于结构优化设计、故障诊断以及健康监测等起着非常重要的作用。由于外载荷很难通过仪器直接测量出来，因此发展了很多确定性的载荷反求方法，也称结构动力学第二类逆问题。然而在工程实际中，用于实现载荷反求时的结构模型参数往往也是未知的或者是不确定性的，这势必导致载荷反求结果是不可信的，而参数识别也称为结构动力学的第一类逆问题。因此，面向第一、二类逆问题融合解决方案具有重要的现实意义。近年来，结构动态载荷及参数联合识别的不确定性方法受到了众多学者的关注，也已成为当前结构动力学领域的一个热门分支方向。

文献［5］中在扩展卡尔曼滤波算法框架下提出了一种EKF-UI（Extended Kalman Filter-Unknown Inputs）算法，来连续识别系统的外载荷及不确定性参数。文献［6］基于EKF和最小二乘估计法重新推导出上述EKF-UI算法应用于弱非线性系统，并指出传统EKF-UI［5］的推导方法相对比较繁琐。文献［7］提出了两步法来连续识别载荷/状态/参数，第一步构造了载荷状态传递方程，并结合测量观测方程，采用标准KF法识别出位置载荷；第二步构造了由状态及参数组成的增广状态传递方程，并基于UKF（Unscented KF）法识别出增广状态向量。文献［8］在扩展卡尔曼滤波（EKF）的框架下，基于参数模型缩减技术提出了A-DEKF（An Augmented Discrete EKF）法来同时在线估计结构的状态/载荷/参数，其主要思想是将结构状态、未知外载荷及不确定性参数三者一并组成一个新的增广状态，再应用标准EKF法来估计该增广状态向量，得到载荷和参数识别值。然而，该方法的成功大大依赖于一个数量级合适的未知载荷方差估计值参与滤波运算，该值的大小对ADEKF算法的估计稳定性影响非常大。文献［9］针对线性系统，基于KF和加权最小二乘算法，提出了未知外载荷和状态的连续最小方差无偏估计滤波法，下文简称GDF法。最近也提出了扩展GDF（Extended GDF：EGDF）算法来联合估计结构外载荷以及不确定性结构参数，其核心思想是将未知参数联合结构状态形成新的增广状态向量，基于GDF法及EKF的非线性系统一阶线性化思想，推导出扩展GDF算法，能够适应于弱非线性系统下的载荷/增广状态连续最小方差无偏估计滤波［10］。不过，该EGDF法中仅采用部分加速度响应作为测量信号参与滤波识别计算，极易导致识别的位移及载荷结果与理论结果存在明显的虚假低频漂移现象。究其原因是加速度信号对于输入载荷的准静态分量不够灵敏，而仅采用加速度响应进行识别，会导致系统的低频振动信号丢失。文献［10-11］采用位移与加速度信号来作为测量响应很好解决了低频漂移的不稳定问题，因为加速度信号和位移信号中分别包含了高、低频振动特性。不过，由于位移传感器通常体积较大，安装位置有要求且易造成结构原始特性改变，并且价格相对于加速度传感器较贵，不太适用于众多工程应用中。

考虑到应变响应与位移响应的对应线性物理关系，也包含足够的低频振动特性。同时，应变计体积小，易于安装，且价格便宜。这里基于多传感器数据融合的策略，应用个别应变响应以及部分加速度响应作为测量信号来扩展原始EGDF算法，以便进行稳定的载荷及参数联合识别。另外，模态缩减法的应用可以提高计算效率，更加适用于工程实际应用。数值算例采用桁架为对象来验证了这里方法的有效性。

2 模态EGDF法

对于含黏性阻尼的n个自由度结构动态系统，其运动微分方程可以表达为下式：

式中：M、C、K—系统质量、阻尼及刚度矩阵，且C一般是n×n的正定或半正定的对称矩阵；p(t)、ṗ(t)、p̈(t)—有限元节点的位移、速度及加速度响应；u（t）—外载荷激励；Bu—外载荷向量的位置影响矩阵。

引入模态坐标变换：

式中：Φ、q(t)—模态振型矩阵和模态位移向量。

将方程代入运动微分方程可得：

其中，Mn=ΦTMΦ=I，Cn=ΦTCΦ=Γ，Kn=ΦTKΦ= Λ，并且存在：

式中：ωi、ζi—第i阶系统无阻尼自然频率和模态阻尼率。

那么，方程可以写成：

定义增广模态状态向量z(t) =(q，̇，α)T。

其中，α=[α1α2…αα]T表示结构的不确定性参数。这里的不确定性参数假定为结构自然频率及模态阻尼率。不过一般来说，结构质量可以看成是恒定不变量，则上述不确定性参数等价于结构的刚度值及模态阻尼率。模态状态运动微分方程变换为状态传递形式为：

系统观测方程可以表达成下式：

式中：H=[ -ΦsΛ -ΦsΓ]，D=ΦsΦTBu，Φs—用于系统识别的s个加速度测量信号所在位置对应的结构振型系数矩阵，矩阵D可以看出为可逆矩阵。

考虑过程噪声，系统的模态状态传递方程以及观测方程可以分别写成如下的非线性时间离散形式：

式中：下标k—第k个采样时刻；y—加速度测量响应；另外，wk—系统噪声，其均值和方差分别假定为0和Gk；vk—观测噪声，其均值和方差分别假定为0和Rk。

定义向量分别是真实值zk、uk在观测向量（y0，y1，y2，…，yk）下的后验估计值，状态方差矩阵假定为另外，假定模态状态的最小方差无偏估计初始值z0|-1及其方差是已知量。基于以上说明，可以推导出用于联合识别载荷/状态/参数的模态EGDF滤波算法，共由三步识别组成，分别是载荷识别步、测量更新步以及时间更新步［8］。这三次识别步如下：

（1）载荷识别步：

（2）测量更新步：

（3）时间更新步：

式中：∇z fk、∇u fk和∇zhk—灵敏度矩阵，其具体表达形式如下式：

其中，

3 应变及加速度响应融合下的EGDF法

加速度传感器因其体积小、易安装，且对结构系统特性影响很小，因而广泛应用于工程实际中来测量结构的振动响应。然而，仅采用加速度测量信号来识别结构系统的GDF算法具有本征的不稳定性，识别出的位移及载荷值会产生明显的虚假低频漂移现象。究其原因是因为加速度信号对于输入载荷的准静态分量不够灵敏［12］。研究表明在部分加速度响应信号的基础上融合个别位移响应信号作为测量信号来联合识别结构的未知外载荷/状态/参数能够极大地缓解虚假低频漂移问题，原因是加速度信号和位移信号中分别包含了高、低频振动特性［10］。然而，位移传感器一般来说体积较大，安装测量时容易造成结构系统的动态特性改变，影响实际测量结果，而且价格也相对较贵。考虑到应变计体积小巧，易于安装，价格便宜，测量响应还包含位移信息，这里将同时应用应变响应和加速度响应来识别未知载荷和结构参数。

应变和位移的数学关系可以表示成［14-15］：

式中：Hε—应变-位移传递矩阵。

将公式应用于EGDF算法中，则观测方程变换成：

式中：vεk—应变观测噪声向量，并假设均值为0，方差为Rεk。

那么，公式中的载荷矩阵Dk变换为：

式中：下标s、udof—测量应变以及未知载荷的数量。

公式变换为：

考虑到应变测量与加速度测量响应的数据融合，传统EGDF算法的公式、分别变换为：

综上所述，这里提出的改进算法仍然包括三步：载荷识别步、测量更新步、时间更新步，对应的公式为（30）、（12）～（15）、（31）、（17）～（20）。为了满足工程中实时识别的要求，可以仅选取结构的前r阶主导模态参与计算即可达到工程精度，而其余的n-r阶非主导模态可以不考虑。本算法流程，如表1所示。

表1 基于EGDF和应变响应的载荷/参数识别流程Tab.1 The Proposed Algorithm Based on the EGDF and Strain Responses

4 数值算例

为了验证这里应变与加速度测量数据融合下的模态EGDF方法的可行性，本节以平面桁架作为数值仿真对象。如图1 所示，平面桁架共包含杆单元31个，且每根杆的横截面尺寸一致，水平杆单元的长度是2m，斜45°杆单元的长度是。所有杆的共性结构参数如下：杆单元的横截面积是8.95×10-5m2，弹性模量是2 × 107Pa，密度是7.85 × 103kg/m3。本例中的每根杆单元采用集中质量单元，是由两个节点组成，每个节点皆含有横向/纵向2个自由度，且节点1和17是固定约束。另外，结构系统阻尼假设为比例型C=αM+βK，阻尼系数分别α=0.1523、β=4.6203×10-4。两个外载荷分别作用于节点4和节点9上，均为竖直方向力（如图1），载荷u1采用双正弦激励形式：

图1 平面桁架结构、桁架有限元模型和传感器布置示意图Fig.1 Plane Truss Structure，Truss Finite Element Model and Sensor Layout Diagram

而载荷u2采用随机激励形式。图1中的黑方格代表加速度传感器布置的位置。

本例中6个杆单元5、7、10、14、15和17的刚度值是不确定的需要与外载荷进行联合识别，假设其初始值分别为759.5N/m、633.0N/m、1342.5N/m、1163.5N/m、759.5N/m、633.0N/m。通常而言，模态缩减法在满足工程精度的同时，能够有效地减小整个计算量有利于整个计算量。本算例采用前7阶主导模态来进行结构的载荷/状态/参数识别。首先，选取7个加速度测量信号来参与识别计算，分别为节点3、4、5、7、9、10的竖直加速度响应信号以及节点9的水平加速度响应信号。5%的环境噪声加在了所有测量响应中。两个外载荷的识别结果，如图2、图3所示。可以看出载荷识别值都出现了明显的低频漂移现象，特别是载荷u1的相对误差已达到29.3%。此外，这里方法也识别出所有节点的状态值，即位移及速度响应。如图4展示的是节点8的竖直位移及速度的理论值与识别值对比图，图中可以明显看出速度识别值的结果很好，相对误差较小，但是位移识别值明显跟随载荷识别值，也同样出现了虚假的低频漂移现象。为了解决上述虚假低频漂移问题，应用这里的应变响应和加速度响应数据融合策略，测量个别单元的应变响应，与上述加速度测量信号一并来联合识别结构未知载荷、状态及不确定性参数，此时新增的两个测量信号分别是单元6、17的竖直应变响应。分别为外载荷、位移和速度的实际值与识别值对比图，如图5～图7所示。

图2 载荷u1的准确值和估计值Fig.2 The Actual and Identified Values of Force u1

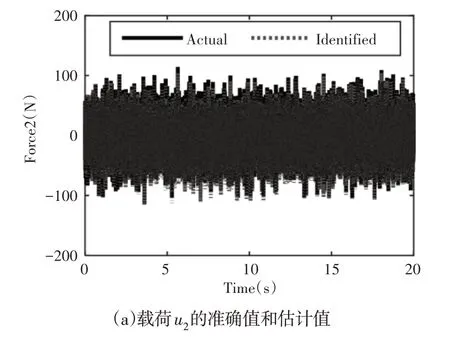
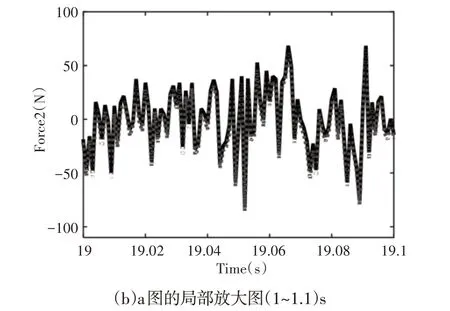
图3 载荷u2的准确值和估计值、a图的局部放大图（1～1.1）s示意图Fig.3 Exact Value and Estimated Value of Load u2 and Schematic Diagram of Local Enlarged View（1～1.1）s of Fig.a

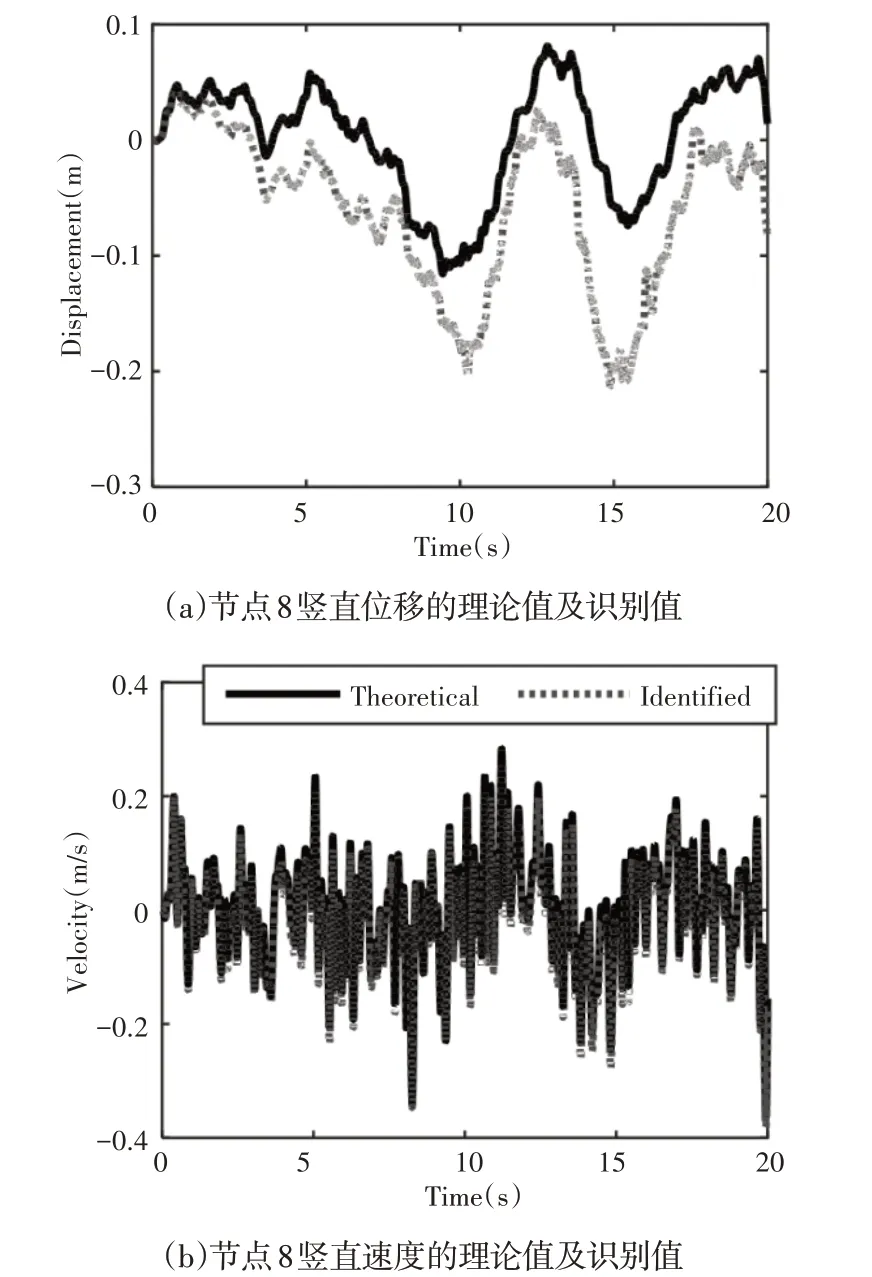
图4 节点8竖直位移、直速度的理论值及识别值Fig.4 Theoretical Values and Identification Values of Node 8 Vertical Displacement and Straight Velocity

图5 采用应变-加速度数据融合下的载荷u1的准确值和估计值Fig.5 The Actual and Identified Values of Force u1 by Data Fusion of Strain and Acceleration Responses

图6 采用应变-加速度数据融合下的载荷u2的准确值和估计值、a图的局部放大图（19～19.1）s示意图Fig.6 Exact Value and Estimated Value of Load u2 under Strain-Acceleration Data Fusion，and Schematic Diagram of Local Enlarged View（19～19.1）s of Fig.a

图7 采用应变-加速度数据融合的节点8竖直位移的理论值及识别值、节点8竖直速度的理论值及识别值示意图Fig.7 Schematic Diagram of Theoretical Value and Identification Value of Vertical Displacement of Node 8 and Theoretical Value and Identification Value of Vertical Velocity of Node 8 with Strain-Acceleration Data Fusion

识别结果的图线与实际值图线基本重合，可以看出这里的数据融合方法可以较大程度缓解载荷及位移识别的虚假低频漂移问题，其中载荷u1识别值的相对误差已降低到4.75%。另外，平面桁架的6 个不确定刚度的识别值，可以看出其识别值十分准确，误差极小，如表2 所示。

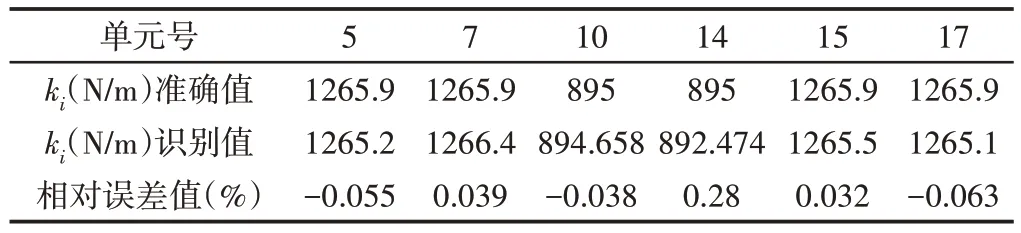
表2 桁架刚度识别值Tab.2 Comparisons of Identified Element Stiffness Parameters of the Truss

上述两种识别方法下的识别结果相对误差对比柱状图，如图8 所示。明显看出，这里的方法识别的载荷及位移相对误差大大降低。综上所述，这里的应变与加速度信号融合对于解决结构的载荷、状态以及参数识别问题具有很强的适用性，很好地解决了此前Kalman 类算法（最小二乘法）的低频飘移现象。

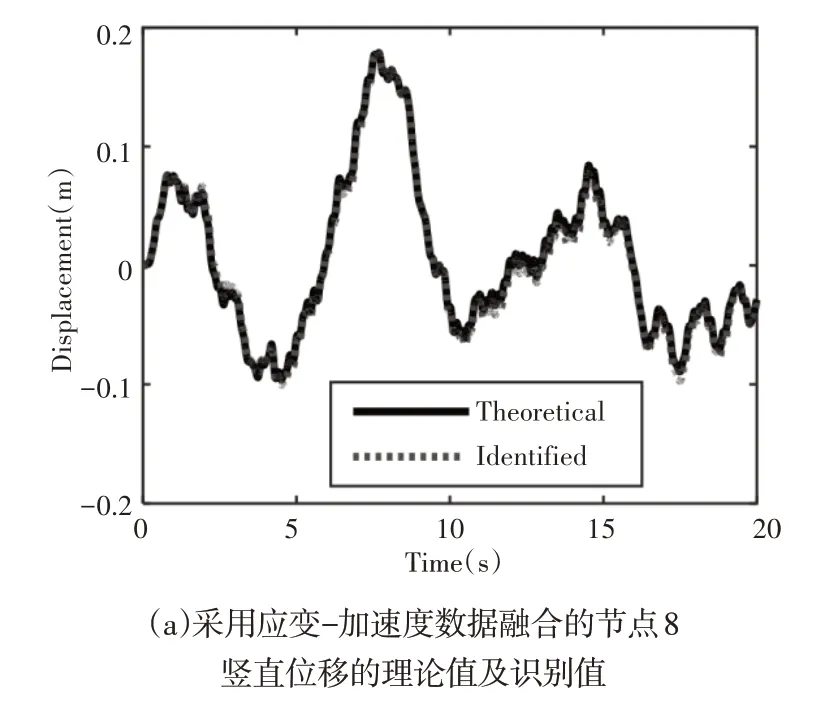
图8 两种方法的识别结果相对误差对比图Fig.8 The Comparison Figure of the REs Obtained From the Two Algorithms

5 结论

这里采用多种传感器信息融合的策略，基于应变测量与加速度测量信号的数据融合，改进了原始EGDF算法来进行线性结构状态、未知载荷及不确定性参数的三者联合识别，且在识别过程中仅需要工程中常用的加速度及应变传感器，同时极大地缓解了位移及载荷识别结果出现虚假低频漂移的不稳定现象。模态缩减法的应用使得本算法更能适应大规模的工程实际案例。数值算例验证了这里方法的有效性。