MCKD与最优小波基结合方法对管道泄漏信号降噪

李志星，王春鹏，鲍慧茹

（1.内蒙古科技大学机械工程学院，内蒙古 包头 014010；2.包头职业技术学院，内蒙古 包头 014030）

1 引言

近年来随着城市的聚集化和现代工业的进一步发展，对管道运输的要求和比重日益增大，但由于管道年久失修，工作环境恶劣导致的腐蚀，裂缝等，容易使管道出现泄露。这些问题的出现轻则将会导致巨大财产损失，严重者甚至会造成重大人员伤亡［1］。尤其是在人口、建筑密集，管道错综复杂的城市背景下，管道的泄漏可能升级为火灾、爆炸等灾难性事件。因腐蚀等原因导致的管道泄漏从而引发事故的例子很多，如台湾高雄一条天然气管道的腐蚀引发了一系列爆炸，造成32人死亡，321人受伤等等。所以对于管道泄漏源的及时发现及定位就显得尤为重要。

管道泄漏主要位于阀门处和传送管道管壁上，对于阀门处的泄露有不少学者已经做了深入研究［2］。针对管道泄漏也已经有了许多检测方法，如空气采样法，人工观察法，此类方法成本较高且效率缓慢。文献［3］使用示踪剂检测法，该方法将示踪剂混到输送管道中，通过观察示踪剂判断管道是否泄露，定位泄露源，但该方法时间周期长且成本较高。文献［4］使用光纤传感器检测管道泄漏，管道泄漏时的冲击会引起光纤发生变形，从而引发光纤的改变，使光纤发生散射或反射，信号产生突变，从而判断是否泄露。但光纤传感器是铺设在管道外侧，成本高且易受环境变化的影响。此外还有文献［5］基于光谱技术及自然目标散射的激光气体检测技术，此方法虽适用于长管线输送的泄露源定位，但成本较高。也有质量守恒法［6］，进口质量等于出口质量，若不等则证明有泄露，此方法虽操作简单，但对于微小泄露误差较大，精度不高。而声发射技术（AE）是近年来新兴的一种无损检测技术，声发射技术由其定位准确度高，敏感度好，响应时间较快，且费用较低的优点，应用比较广泛。声发射信号是指由于材料或构件在受力过程中产生变形或裂纹，以弹力波的形式释放应变能的现象。这些弹性波会携带着材料损伤部位的信息，通过收集并分析这些信息我们可以得到材料损伤的特征。油液或气体的泄漏与管道的剧烈摩擦会产生声发射信号。但由于管道多为中低压管道［7］，所以细小裂缝的泄露问题往往由于硬件检测难度大，不易识别与分析，且泄露信号在传输过程中受到噪音的影响，使信号的采集与处理难度增大，所以对信号加强与过滤就尤为重要。

声发射中对信号的处理方式有很多，文献［8］采用的最小熵解卷积（MED）就是基于峭度提出的一种旨在抵消传输路径噪音影响的方法。但同时，MED 也存在模态混叠与端点效应等问题。文献［9］在此基础上提出了最大相关峭度解卷积算法（MCKD），解决了MED方法只对单脉冲信号具有凸显作用的特点，可以实现对周期性信号脉冲进行提取的目的。文献［10］将MCKD应用在齿轮故障方面，用来提取淹没在噪声信号中的齿轮故障信号，来达到降噪的目的。文献［11］采用MCKD方法对齿轮故障信号进行凸显降噪后进一步采用EEMD方法对信号进行局部信号特征提取。MCKD方法中周期T和滤波器长度L的参数选择对MCKD方法降噪效果的影响十分关键。文献［12］基于网格搜索法选取最优参数，但其选取的最优参数存在一定偏差，且只针对一定范围信号，并且需要自己设计合理的采样频率。MCKD方法应用于齿轮故障诊断已经较成熟，对于管道泄漏方向，MCKD方法还没得到很好的应用。而MCKD处理的信号虽然对其传输路径的噪音及冲击信号的凸显有很好的效果，但对局部特征的展现效果不好，所以我们使用小波变换［13］进一步分析去噪，其中小波基的选择对小波变换效果至关重要。

综上，先利用局部信噪比的方法来选取MCKD 参数，并将MCKD方法应用到管道泄漏上对采集到的信号进行前期的过滤与加强，消除传输路径对信号的影响。然后选择小波基对加强之后的信号进行进一步降噪处理，对比几种小波基处理之后的信噪比，选出最优小波基。

2 MCKD的原理与参数选择

2.1 MCKD方法原理

MCKD 是从MED 方法不断改进来的，MCKD 能充分考虑冲击成分的连续性和周期性。其最早应用在齿轮轴承的故障检测上，目的是减少传输路径的对信号的影响，提高信号强度。MCKD是以相关峭度为标准，通过解卷积算法来凸显信号中被噪声掩盖的有用的冲击成分，从而更直观的展现出冲击部位的信号。

周期信号的相关峭度可以表示为：

式中：M—移位数；T—冲击信号的周期；n—信号的采样频率。

对于输入为xn输出为yn的信号。移位数M的增加会使周期性脉冲数量增加，从而提高信号检测能力。但过大的M将会导致检测精度的丢失。根据经验M的取值为：（1～7）。

MCKD以相关峭度最大为目标函数，即滤波器的选取需满足相关峭度最大，表达式为：

为了得到使CKM(T)取得最大值的最优小波滤波器求解方程，令：

求解上式得：

则MCKD的迭代求解过程如下：

（1）选择最优参数，确定滤波器长度L，移位数M，冲击信号周期T。

（2）计算原信号X(n)的XnXnT和XmT。

（3）求得降噪后输出信号y(n)。

（4）根据y(n)计算αm与β。

（5）更新滤波器系数f。

如果经过滤波前后的信号ΔCKm(T)＜ε，则停止迭代，反之，则跳回（3），ε是控制迭代次数的较小正数。

2.2 MCKD的参数选取

MKCD滤波方法受输入参数的影响较大，包括移位数M，滤波器长度L，冲击信号周期T等。要想达到最优的滤波效果就要选取合适的参数进行降噪。

参数M的选取：M一般可在（1～7）内取任意值，由于数据范围小，所以采用枚举法对M的取值进行选择，将M设定为1。

参数T的选取：参数T是影响MCKD方法的降噪效果的重要参数，输入不同的周期参数，则信号中的其他的周期信号将被过滤降噪。只有MCKD方法中的周期参数的选取与管道泄漏处的冲击信号的周期相等时，才能达到滤去干扰信号，增强冲击信号的最佳效果，MCKD方法才能对噪音信号进行最有效的过滤。但在实际工程中，冲击信号的脉冲间隔是未知的，这就要求我们根据信号的波形图计算推测出信号的脉冲间隔，并以此作为MCKD方法的周期参数。由于管道泄漏信号是非平稳性周期信号，其周期特性虽有表现，但变动较大，这就导致参数T的选择至关重要，T选取过大会使MCKD方法起不到滤波效果。选取T过程如下：（1）选取极值点：根据信号的波形在一定范围内选取极值点，为了消除噪音信号的影响，极值点的选取要依据在每一个信号段取得极值后，需要对端点域内的极值进行极差控制，取一个信号极值点后要与左右方向的几个信号端点进行比较，进行差值控制，使差值超过一个规定的范围，则认为是一个信号极值点，反之，不是极值点。（2）设定一个合理范围内的MCKD滤波器长度L，同时避免滤波器长度的不合理对周期参数选择的影响，选取参数L为150。（3）根据选出来的极值点之间的周期参数，用MCKD方法进行运行处理，选择最优的信号周期参数。

参数L的选取：滤波器长度过大会导致数据计算量大，从而故障分析诊断时间过长。滤波器长度过短则会导致MCKD方法不能起到很好的滤波降噪效果。文献［14］通过计算局部信噪比的方法评价MCKD方法的效果。SNR的大小可以很直观的展现出降噪效果的好坏，信噪比越大则信号降噪效果越好；反之，基于此采用对比信噪比大小的方式对参数L进行寻优处理，信噪比越大说明降噪效果越好，参数L越优。

3 小波变换的定义

小波变换是对信号进行时间频率的局部化分析，它通过缩放和平移运算以匹配输入信号，对信号逐步进行多尺度细化，最终达到在高频处时间分辨率高，低频处频率分辨率高，能符合我们对信号分析在高低频的分辨率要求，从而可进行对信号的局部化特征提取。因此小波变化是对非平稳信号的处理十分有效，小波变换能在时域和频域都具有良好的局部化分析优势，对噪声滤除的同时实现对有用信息的特征的保留。

设想x(t)是平方可积的函数，ψ(t)为母小波函数，则小波变换定义为：

4 实验分析

4.1 管道泄露信号的采集

不同管道材质与形状都会对实验收集到的信号造成影响。实验采用不锈钢材质管道，其长度为3000mm，外径160mm，壁厚8mm。管道的泄露源为一处开口5mm 的泄露源，管道放在玻璃支架上，以减少外在噪音或震动带来的影响，如图1所示。实验采用模拟输油管道在背景噪音和管道周期频率外部敲击噪音与管道小泄露同时存在的情况下进行信号的采集。此情况下采集到的声发射信号更适合实际情况下的管道泄漏信号。用传感器收集管道泄漏信号并进行分析。

图1 管道泄漏声发射信号采集装置Fig.1 Pipeline Leak Acoustic Emission Signal Acquisition Device

传感器收集到的信号时频域，如图2所示。

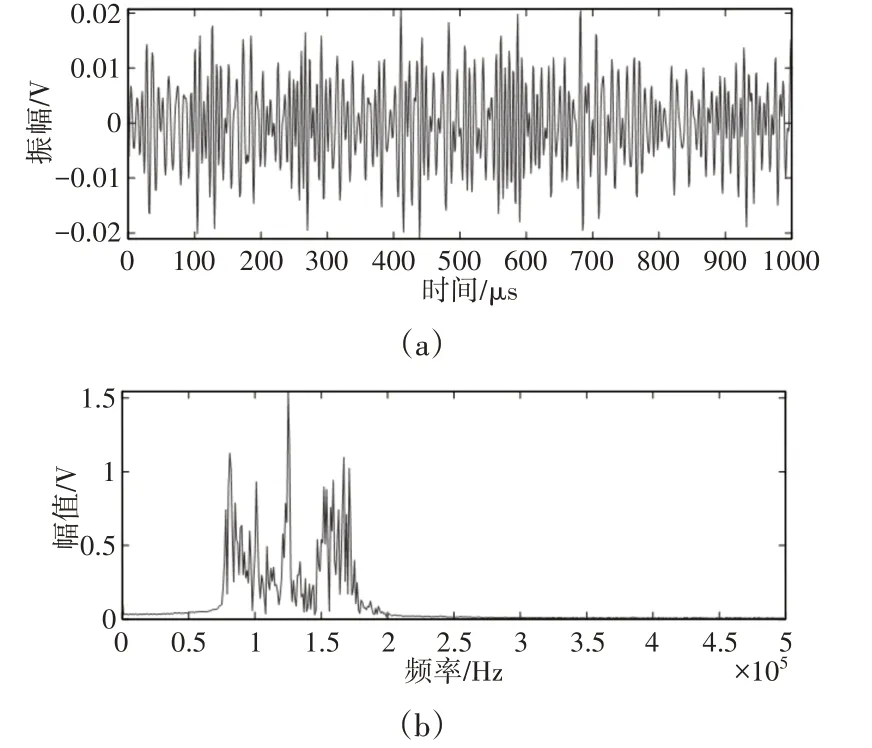
图2 原信号的时频域波形图Fig.2 Time-Frequency Domain Waveform of the Original Signal

对原信号进行MCKD处理，如图3所示。

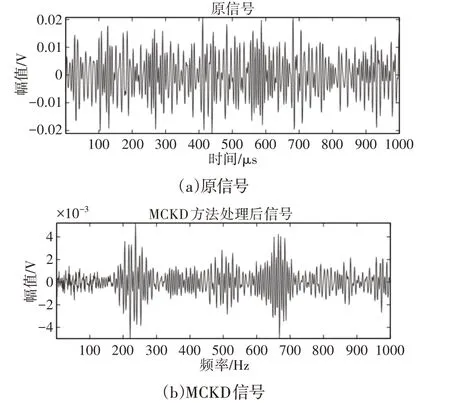
图3 原始信号与MCKD信号对比图Fig.3 Comparison of Raw and MCKD Signals

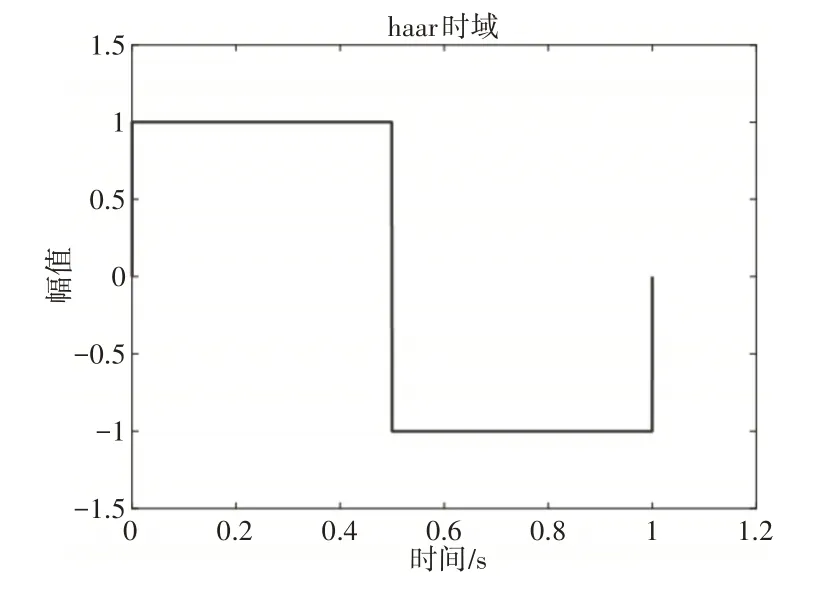
图4 haar小波基时域波形图Fig.4 Haar Wavelet Base Waveform in Time Domain

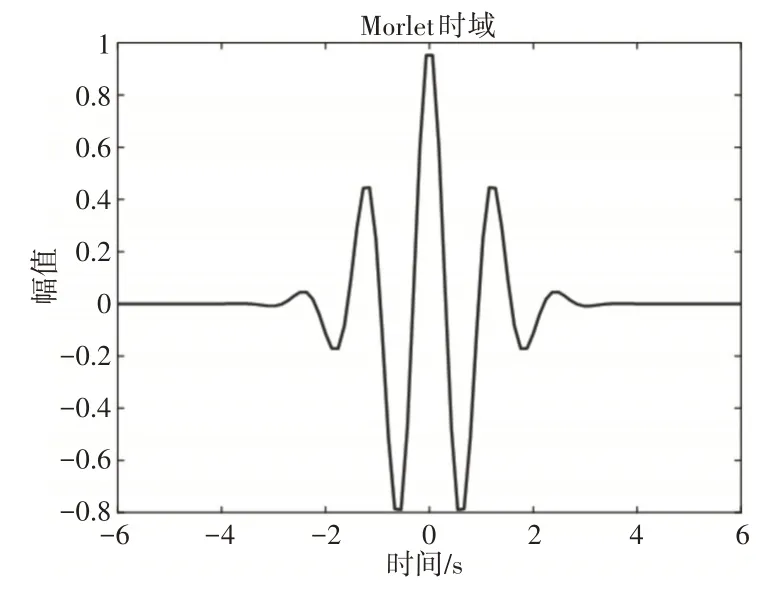
图5 Morlet小波基时域波形图Fig.5 Morlet Wavelet Base Waveform in Time Domain

图6 Mexihat小波基时域波形图Fig.6 Mexihat Wavelet Base Waveform in Time Domain

图7 db4小波基时域波形图Fig.7 db4 Wavelet Base Waveform in Time Domain

从原信号与处理后的信号波形图对比中看出MCKD方法能有效的对管道泄漏信号在传播路径中受到的无序噪音信号进行滤除，使冲击信号得到加强，但是MCKD方法不能对信号进行更细化的分析处理，从而不能对信号进行局部特征的提取，限制了对管道泄漏部位的准确定位。为此，我们使用小波变换的方法对处理之后的信号进一步降噪。

4.2 小波基的选择

小波变换的关键在于小波基的选择，小波基选择的依据并未统一，但选取小波基的原则上是与原始信号的相似度最大的为最优小波基。相似度不高的小波基会影响信号分析的局部相关性。为了找出最适合的小波基，根据文献［15］对比经MCKD方法处理过的信号与下列四种小波基的时域波形图，找出最优小波基。

对比MCKD处理后信号波形图与上述四种小波基时域波形图，可以看出处理之后的信号波形图与db系列小波基波形最接近，下面就不同的db小波基使用MATLAB软件来进行小波变换，分析SNR与MSE找出最优小波基。

由表1可以看出，随着db小波基的阶数的增大，信噪比也随之增大，降噪效果越好，于是增大小波基的阶数到db40，得其信噪比。信噪比越大说明处理效果越好，均方差越小说明处理效果越好。通过表1中db小波基对信号的降噪处理结果中可以看出，db40是相对来说效果更好的一种，无论从信噪比还是从均方根误差来看db40都更适合用于管道泄露信号降噪，更准确的对泄漏源进行定位。

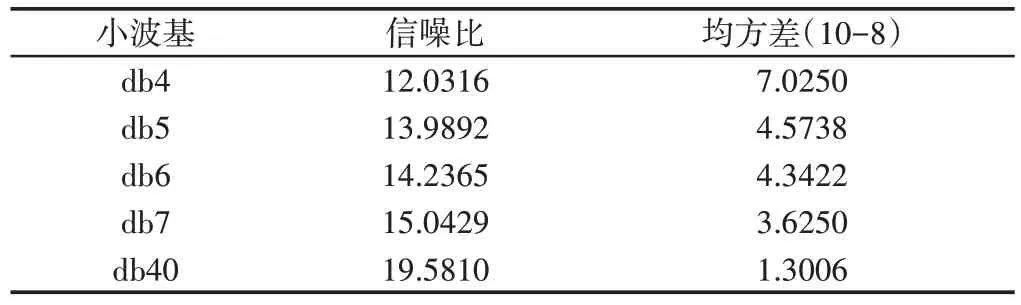
表1 五种不同小波基降噪结果分析Tab.1 Analysis of Five Different Wavelet Base Noise Reduction Results

5 结论

通过对管道声发射信号的收集与分析得出：（1）管道声发射信号收集受外界干扰较大，为了实现对声发射信号更好的分析，采用MCKD方法对其进行传播路径的降噪以及对信号冲击成分的凸显是一种很好的方法。（2）小波变换对信号的时域和频域的都能进行很好的局部化分析，在去除信号噪音的同时能很好地保留信号的特征信息。（3）MCKD方法处理之后的信号采用小波变化对信号进一步处理的方法，能很好的解决MCKD方法中对局部分析能力较弱的情况。（4）db40小波基相比其他小波基降噪效果更加明显，也更适合实际工程应用。