TC-SAW滤波器仿真与设计技术

陈晓阳,苏 波,叶 志,史向龙,范佰杰,张俊茜,于倩至

(北京无线电测量研究所,北京 100854)

0 引言

声表面波(SAW)滤波器具有小型化、高性能的优势,被广泛应用于雷达、导航、通信、电子对抗等领域,但由于普通的SAW滤波器在温度变化时频率漂移较大(温度系数约为(-90～-30)×10-6/℃),严重影响了其在全温下的有效带宽、有效阻带等电性能,进而影响了整个系统的技术指标。为解决此问题,高温稳定性SAW(TC-SAW)滤波器是满足系统全温工作要求的最佳手段。

TC-SAW是对普通SAW滤波器温度系数的一种改进技术。一种方法是采用生长正温度系数的SiO2补偿负温度系数的基底[1],以达到温度补偿的效果,通过温度补偿薄膜及控制电极形貌降低滤波器温度系数。该技术可将滤波器的温度系数由(-90～-30)×10-6/℃降低到(-20～0)×10-6/℃[2],故在对高温稳定性、小型化要求高的电子设备中有巨大的指标优势和应用价值。另一种方法是通过将铌酸锂或钽酸锂薄膜材料键合到具有正温度系数的石英材料或膨胀系数较小的蓝宝石、硅材料上,以降低材料的膨胀系数来实现温度系数的补偿。

TC-SAW衬底由最初的128°铌酸锂发展成为5°、15°YX切等多种切型[3],以满足不同带宽的滤波器设计。同时,钽酸锂也有多种切型被用作TC-SAW衬底材料[4]。结合切型与SiO2薄膜的厚度调控可以设计出不同机电耦合系数的器件。因此,TC-SAW技术在设计不同带宽滤波器方面具有更大的灵活性。SiO2薄膜的成膜技术不断进步,薄膜中的声损耗越来越小,TC-SAW器件的品质因数(Q)值已远超常规SAW,在2 GHz时,其Q值最大可达2 500(常规SAW的Q最大为1 000),一般称为HQ-TC-SAW[5]。

本文主要介绍了一种TC-SAW滤波器技术,上温补溅射SiO2的温度补偿SAW滤波器。

1 TC-SAW设计流程

TC-SAW滤波器由于涉及多层材料的组合,比单晶材料的声表面波器件复杂,整个研究方法也更复杂,设计方法更灵活,主要包括以下4个研究步骤:

1) 首先需要确定温度补偿结构的温补材料及压电材料的属性,并在性能和温度系数之间求取合适的层间参数。

2) 在合适的层间厚度基础上,利用无限周期层状FEM/BEM理论[6]提取耦合模式模型参数数据库,并置于设计仿真软件中,最终实现TC-SAW滤波器的COM设计优化。

3) 采用有限长二维层状FEM/BEM理论对器件进行精确验证。

4) 层状材料通常存在横向模式耦合。采用微结构对横向模式进行抑制,为此需要建立三维理论模型进行声学模态分析。图1为整个设计流程图。

图1 TC-SAW设计流程图

纵向耦合多模SAW滤波器的设计主要采用耦合模(COM)分析法。COM模型的基本思想:栅格内同时存在多个传播声波模式,通过栅格阵内指间反射相互耦合;同时,外加电压通过栅格的换能作用又激发出向多个方向传播的声波模式,这些声波模式间存在一定的线性关系,可用COM方程表征[6],并以此为设计依据。

2 层状结构FEM/BEM原理

相比于单层结构,层状结构的FEM/BEM理论更复杂。对于上温补层结构(见图2),需要在单层FEM/BEM理论的基础上将温度补偿层部分采用FEM进行计算,温度补偿层上面及衬底同样采用BEM理论进行精确计算,最终得到向上多层的二维层状FEM/BEM仿真模型。对于下温补层的键合片结构(见图3),将多层衬底结构作为整体,采用BEM理论计算层状结构的格林函数,电极部分同样采用FEM理论计算,二者结合最终得到向下多层的二维层状FEM/BEM仿真模型。

图2 TC-SAW上温补层结构

图3 TC-SAW下温补层结构

通过设置无限周期边界条件及有限结构周期边界条件,分别可以得到基于无限周期的层状FEM/BEM模型及有限长层状FEM/BEM模型。通过建立上述模型可以计算出整个结构的电端口导纳特性。在此基础上增加了计算复合材料的温度系数、高功率复合电极结构、描述工艺特性的电极角度、多温补层结构、表面钝化层及场分布等功能。

3 层状结构COM模型原理

COM模型的基本思想是设想换能器内同时存在右向和左向平面波,它们通过换能器内的指间反射相互耦合,且换能器的换能作用又同时激发右向和左向的平面波[7]。假设这些作用限于线性范围,各个作用可互相线性迭加,则这两平面波之间应满足一定的关系。设R代表右向平面波,S代表左向平面波,则一般性的耦合模式方程可写为

(1)

(2)

(3)

其中:

Δ=k-k0

(4)

(5)

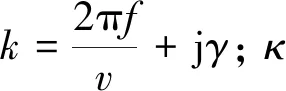
由式(1)可以看出,COM方程包含κ、α、C、v、γ5个基本参量。只要得到这些COM参数,就能准确地描述器件的性能。

对于128°-铌酸锂材料上的TC-SAW存在无衰减的瑞利波模式,COM参量退化为4个参量即可描述TC-SAW中的瑞利波。若采用随频率变化的色散COM参量[8],仿真精度可进一步提升。

4 FEM/BEM与COM模型的结果对比

通过无限周期层状FEM/BEM软件计算了相应的COM参量提取结构,提取不同温补层SiO2厚度、不同金属膜厚、不同金属化比下的三维COM参量库,形成了TC-SAW的仿真软件。与实验提取COM参量不同,该软件可仿真任意频率、任意SiO2厚度、任意金属膜厚、任意金属化比下的滤波器性能。在提取COM参量前,需要对多层FEM/BEM软件进行实验修正才能保证COM仿真结果与实验结果吻合良好,同时保证了优化设计的有效性。

利用层状FEM/BEM理论对COM仿真结果进行验证,结果对比如图4所示。由图可见,COM仿真结果与FEM/BEM结果在通带和近阻带抑制频率相吻合,当频率到达慢切变体声波截止频率位置时,性能略有差异;同时COM模型取1 000个频率点的仿真时间在1 s内。因此,无论仿真精度还是速度都完全能够满足优化设计的需要,这充分证明了目前COM模型的有效性。

图4 TC-SAW滤波器COM与层状FEM/BEM对比结果

5 TC-SAW材料选取及模态分析

5.1 128°-铌酸锂表面溅射SiO2的TC-SAW结构

128°-铌酸锂单晶材料上的瑞利波温度系数达到-90×10-6/℃,而机电耦合系数通常仅约4%,并且由于反射系数较低,基本无法设计出高性能、小体积且满足高、低温使用的低损耗滤波器。在128°-铌酸锂单晶材料上溅射具有正温度系数的SiO2材料,可以将温度系数补偿到(-40～0)×10-6/℃。图5为溅射SiO2的基本结构示意图。

图5 TC-SAW上温补层结构

5.2 模态分析

图6为TC-SAW上温补层结构在不同欧拉角下随SiO2、Cu电极厚度变化的关系[9]。由图可见,当SiO2的厚度(hSiO2)分别为0、0.2λ,0.3λ,0.4λ(其中λ为波长)时,SiO2/Cu/LN结构激发的是瑞利波模式。当hSiO2=0.3λ,Cu电极厚度(hCu)=0.05λ,欧拉角达到(0, 38°,0)时,此时即是通常的128°-铌酸锂,瑞利波的机电耦合系数达到最大,该条件下的机电耦合系数达到8%,理论上可实现4%左右相对带宽的低损耗TC-SAW滤波器。当hSiO2=0.3λ,hCu=0.05λ,欧拉角达到(0,90°,0)时,漏表面波(LSAW)被激发,此时的LSAW机电耦合系数达到16%,利用此切型及厚度,理论上可实现相对带宽约8%低损耗TC-SAW。

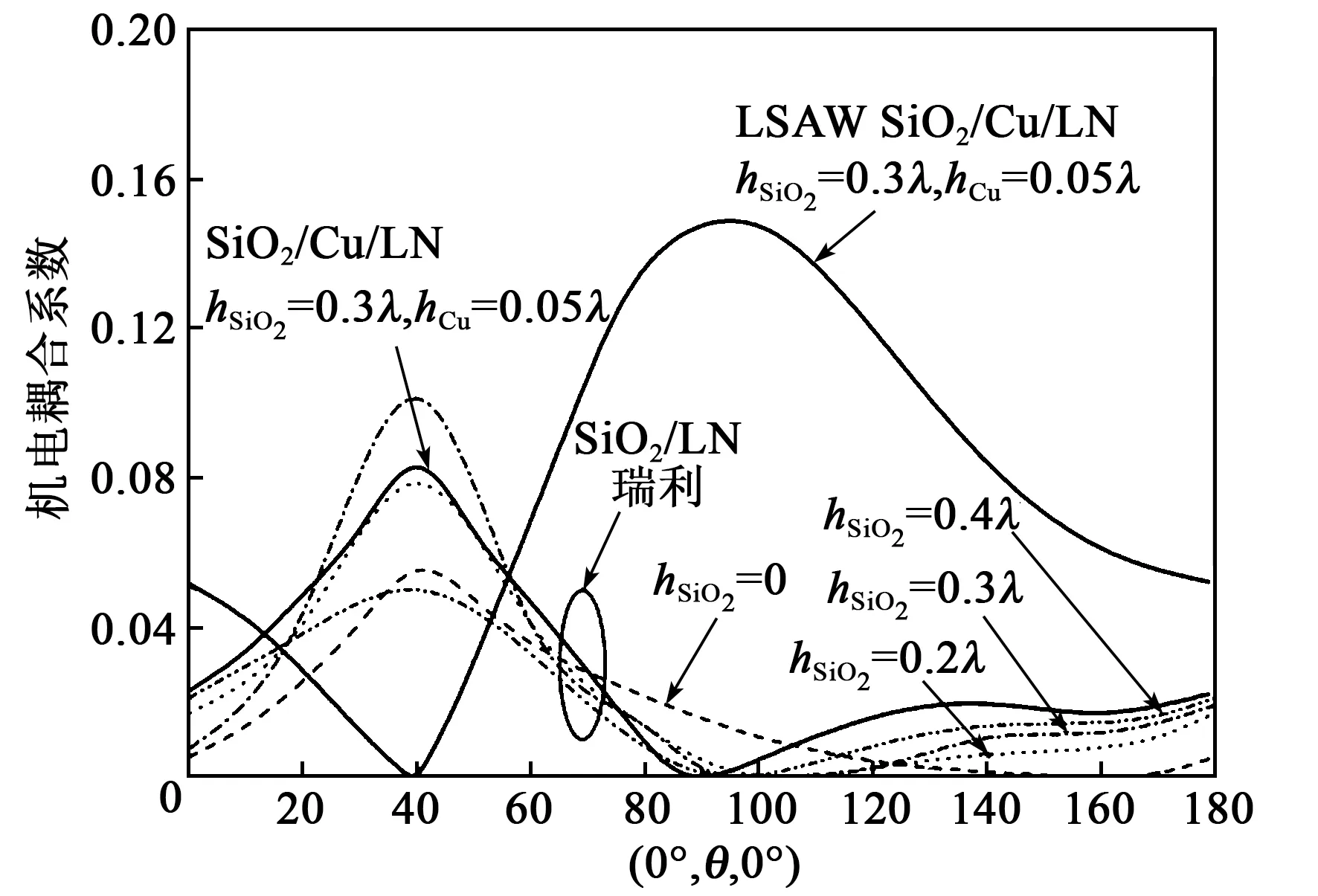
图6 TC-SAW上温补层结构随欧拉角的变化规律

对于要求相对带宽在4%内的TC-SAW滤波器,可以采用128°-铌酸锂上溅射SiO2结构实现要求的性能指标。利用FEM/BEM计算了SiO2/Cu/128LN结构在hSiO2=0.3λ、hCu=0.05λ;hSiO2=0.35λ、hCu=0.05λ时的温度系数,得出其温度系数为(-15～-10)×10-6/℃,该条件下可实现温度系数约为-10×10-6/℃的TC-SAW滤波器。为保证该条件下具有良好的性能,设计了性能良好的低损耗滤波器,分别计算该条件下的机电耦合系数、品质因数(Q)值的变化规律,如图7、8所示。图8中,Qr为谐振系数,Qa为反谐振系数。

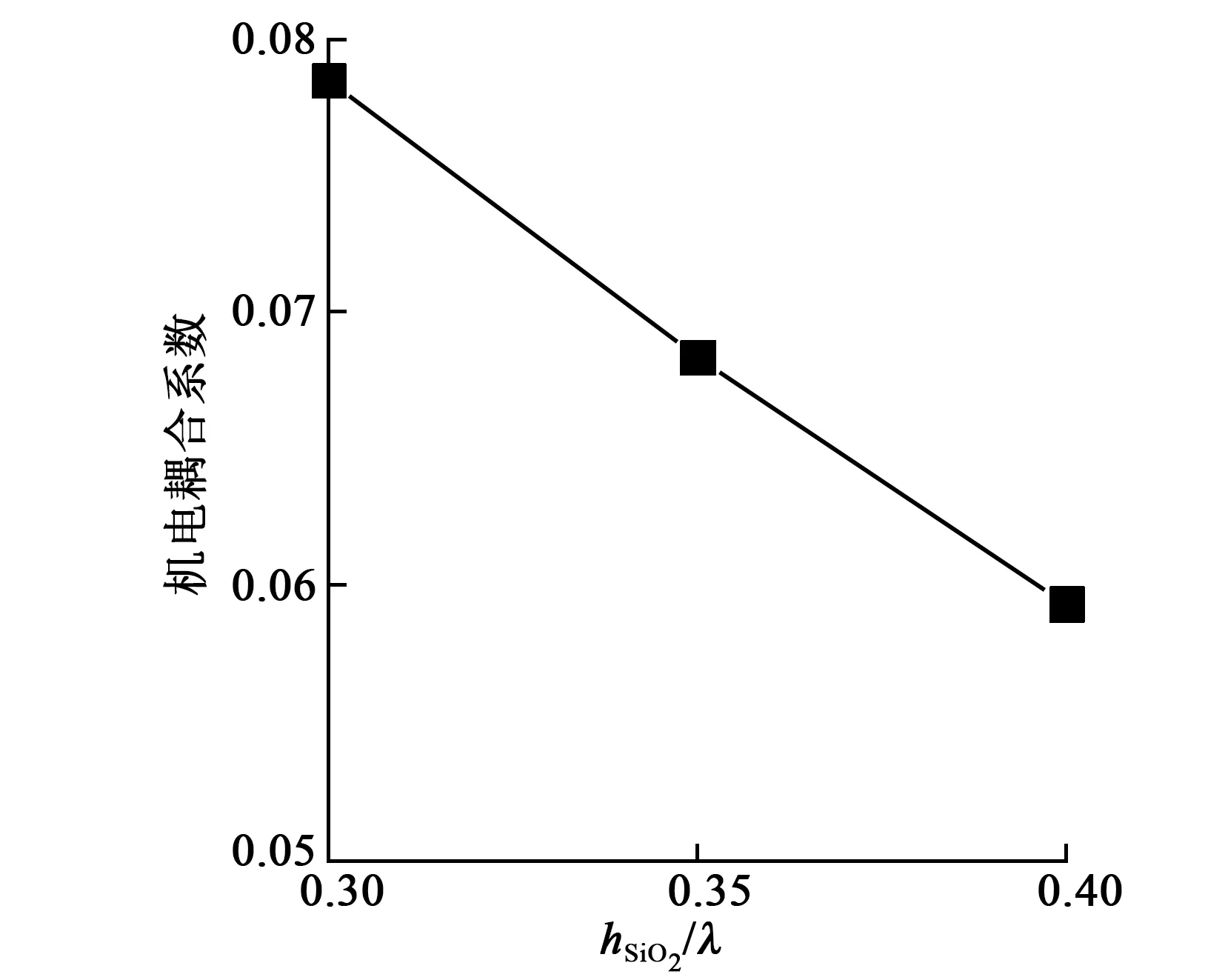
图7 TC-SAW随温补层厚度变化机电耦合系数规律

图8 TC-SAW随温补层厚度变化Q值规律

由图7、8可见,随着SiO2相对厚度的增加,机电耦合系数逐渐降低,同时Qr、Qa值也逐步降低。

5.3 横向模式抑制

多层材料复合结构因存在横向模式将造成谐振频率和反谐振频率之间的杂波干扰,降低了谐振器的Q值,进而造成滤波器通带波纹变大[10],如图9所示。

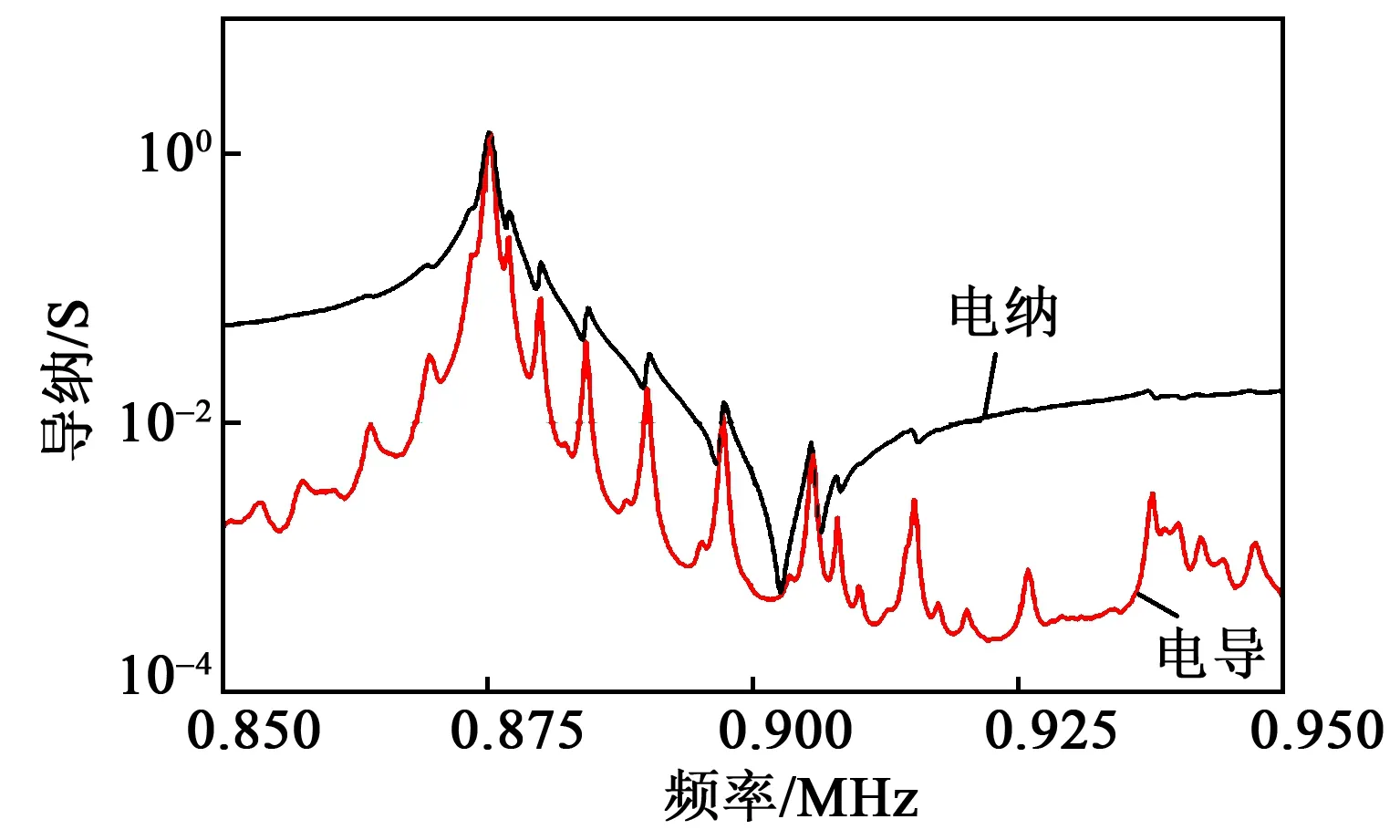
图9 TC-SAW谐振器横向模式

为了降低横向模式干扰,并进一步提高Q值,需要设计Piston的边界条件[11],将能量控制在有效的振动区域(见图10)。图中,A为振幅,Wg为波导孔径,Ws为边界宽度。

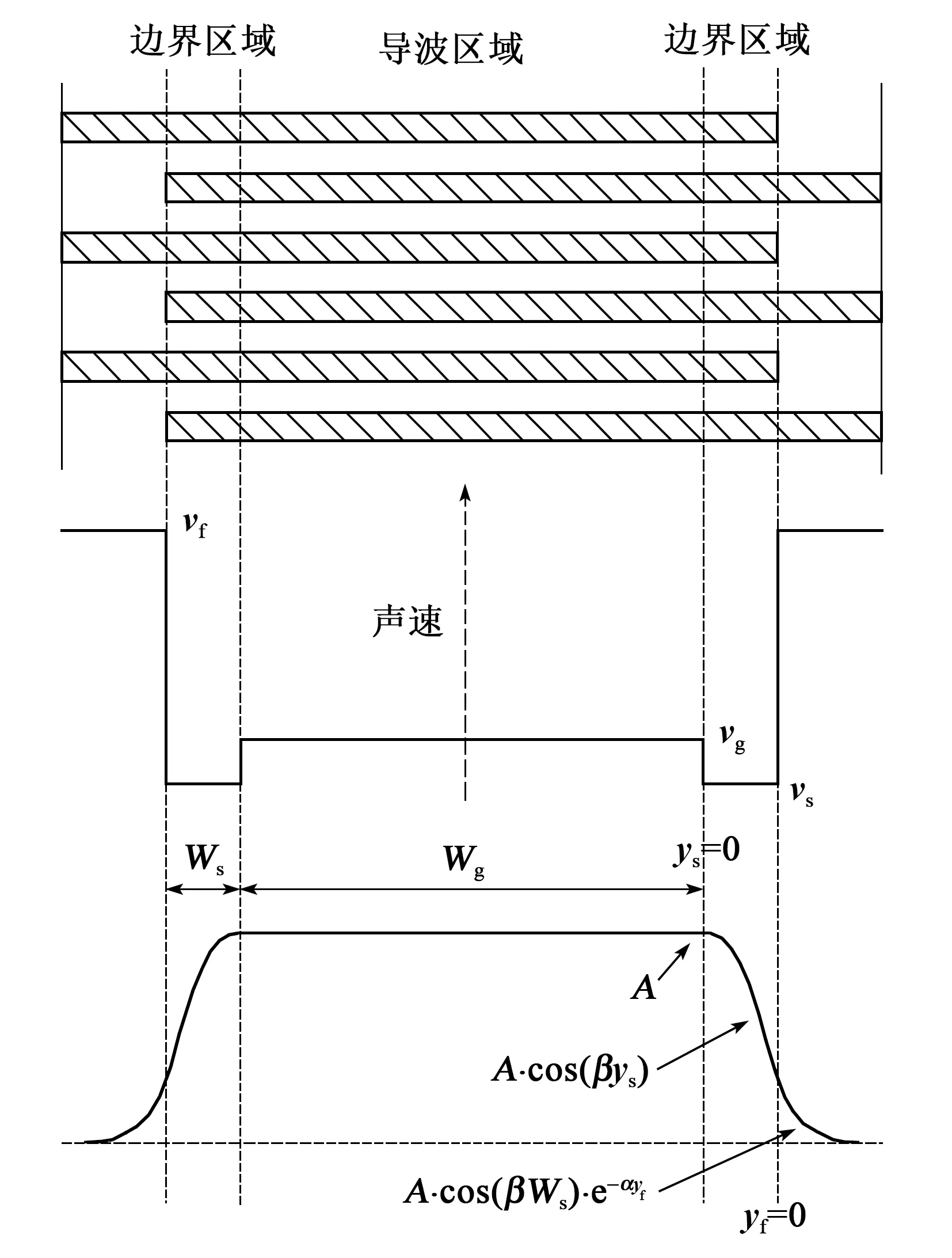
图10 TC-SAW谐振器横向模式场分布

图11、12分别为抑制横向模式后的谐振器导纳特性及Bode-Q。图中,f/f0为归一化频率。由图11、12可以看出,横向模式基本消除,且Q值提升了1倍。

图11 TC-SAW谐振器横向模式抑制后的导纳

图12 TC-SAW谐振器横向模式抑制后的Bode-Q

6 优化过程及验证结果

综合考虑温度系数和性能需求,在给定的SiO2厚度、金属电极厚度下,利用COM软件进行优化设计。采用非线性全局优化设计,其中指条的周期、数量、占空比、孔径作为待优化变量,通过不断更改待优化参量取值,从而逼近目标要求结果。

6.1 优化过程

优化开始前,首先根据目标值完善目标函数的要求,然后确定给出待优化参量的初始结果,绘制电磁版图,通过HFSS软件计算所有电磁效应S参数。通过COM仿真设计平台软件中全波仿真功能中的声电协同仿真接口代入电磁效应S参数,可以计算包含叉指声学响应、版图、基板、封装、测试版等总的电磁效应在内的声电协同全波仿真结果。使用优化设计功能可得到所能到达的最好仿真曲线。最后通过多层FEM/BEM精确声学验证及HFSS得到电磁仿真参数,最终得到准确的仿真结果。为保证窄带特性,采用基于M推演的阻抗元结构[12]。

当声学初始值已满足性能要求时,需要绘制电磁版图。通过HFSS软件建模,模拟芯片中电性能影响及压焊封装,并计算所有电磁效应S参数,HFSS建模如图13所示。

图13 TC-SAW滤波器HFSS建模图

6.2 优化设计结果及性能分析

优化中采用多参量离散变量模拟退火全局优化算法,给出优化变量的初始值及优化步进,从初始温度开始退火,经过3次退火即可得到一轮稳定的结果,整个过程的时间约为2 h。

针对窄带高矩形度TC-SAW滤波器的需求,优化了一款TC-SAW滤波器。图14、15分别为FEM/BEM仿真验证结果与实测结果的对比图。

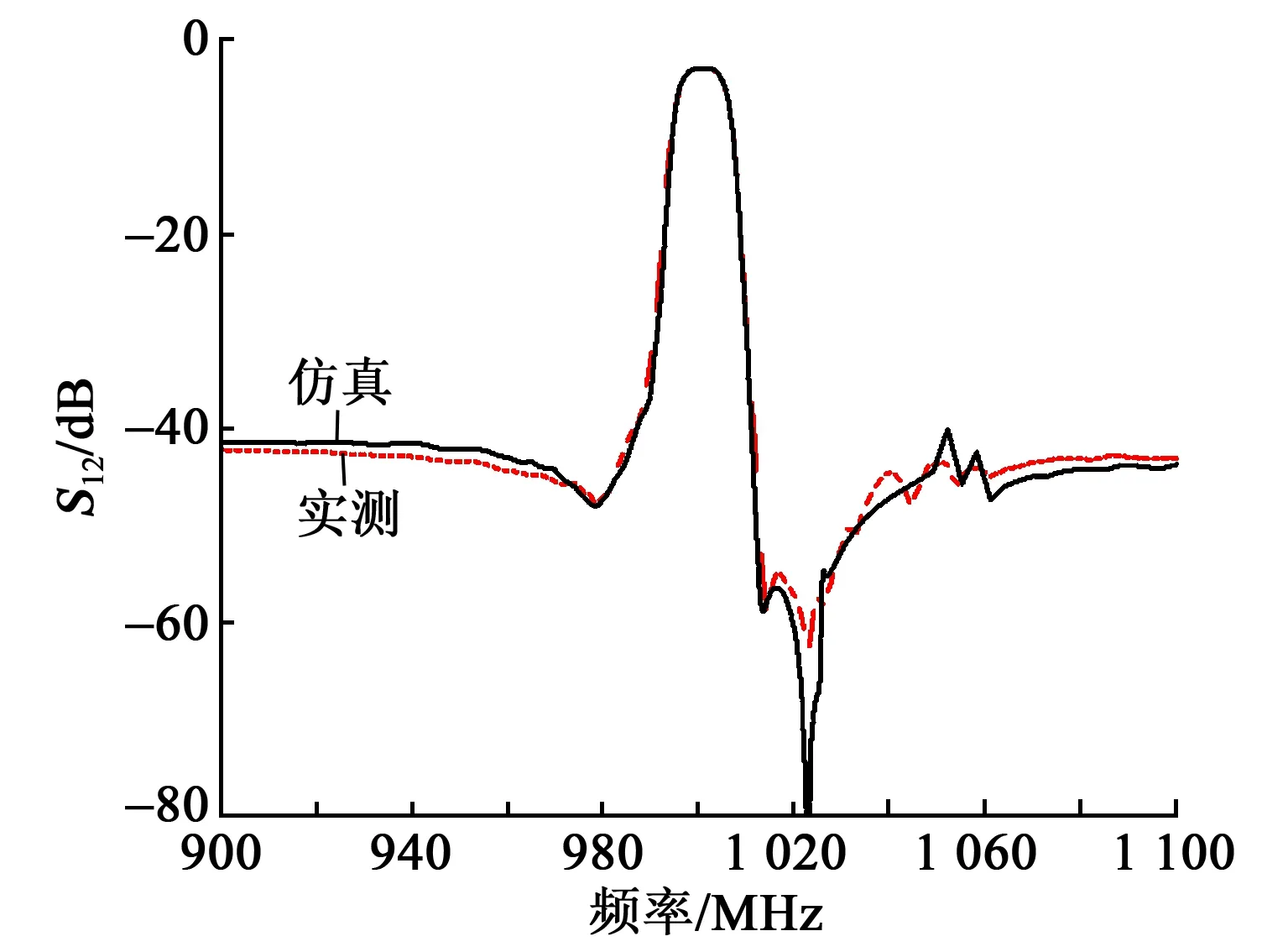
图14 窄带TC-SAW滤波器仿真实测对比图(近阻带)

图15 窄带TC-SAW滤波器仿真实测对比图(远带)

由图14、15可见,仿真结果在较宽的范围内与实测结果吻合良好。同时在1 250 MHz处有一个杂波,为快切变体波截止频率,FEM/BEM也可准确地仿真出来,这是COM模型做不到的。

图16为该TC-SAW滤波器在-55～+85 ℃的实测曲线。通过对不同温度下的实测曲线计算,得到通带内的温度系数约为-5×10-6/℃。

图16 窄带TC-SAW滤波器三温性能

7 结束语

本文给出了一种TC-SAW滤波器的详细设计方法,通过研究不同温补层厚度、电极厚度变化下,随欧拉角变化的下瑞利波、漏表面波的机电耦合系数变化,给出了最佳的欧拉角及结构设计参数。在此基础上,为了抑制横向模式,通过设置Piston边界条件,有效提升了谐振器Q值;提取三维COM参量库,并形成仿真及优化设计软件,最终设计出满足要求的TC-SAW滤波器。实验结果充分证明了仿真及设计方法的有效性。