压电力传感器中晶轴偏转产生的维间耦合研究

张 军,王郁赫,任宗金,李新阳,滕玄德

(大连理工大学 高性能精密制造全国重点实验室, 辽宁 大连 116024)

0 引言

压电传感器以其体积小,刚度高[1]及动态特性好等特点,广泛应用于机械加工、航空航天、力和加速度等物理量的测量与反馈。然而传感器在使用时都会出现一定的维间耦合或串扰[2]现象,限制了测量精度。针对此问题,人们主要从结构解耦[3]和算法解耦[4-5]两方面控制。邵俊等[6]分析建立了压电测力单元结构装配偏差引起的耦合输出模型。任宗金等[7]提出基于标定矩阵的传感器输出补偿方法,将维间耦合控制在2.1%内。以上方法均减少了传感器维间耦合或串扰,提高了测量精度,但对敏感材料本身引起的耦合研究较少。在晶体切割与装入传感器过程中,由于误差存在,材料晶轴偏转,从而引起干扰压电效应,产生传感器维间耦合现象。本文以压电石英力传感器为研究对象,推导建立含晶轴偏转的维间耦合公式进行仿真验证,并从控制传感器耦合角度出发,给出偏转容差范围。

1 维间耦合公式推导

1.1 传感器结构与维间耦合现象

图1为力测量坐标系及传感器结构,压电石英三向力传感器包含3组石英晶组,每组各包含2片石英晶片。两组Y0°晶组用于测量平行于晶片表面的力(Fx和Fy),一组X0°晶组用于测量垂直于晶片表面的力(Fz),实现三维力正交测量。使用时传感器组装成测力单元。组装时通过预紧螺栓、螺母实现自预紧,通过摩擦测量侧向力(Fx和Fy)。

图1 测量坐标系与传感器结构

单元固定在加载台上,如图2(a)所示。当Fz向加载到12 kN时,Fy向测量输出225.89 N,Fx向输出-72.44 N。理想情况下,不同方向测量应独立互不影响,Fz向加载下,Fx、Fy向无输出。

图2 传感器加载时维间耦合现象

维间耦合现象产生原因包括结构装配偏差、力源加载偏斜及敏感材料偏差等。下面将探究敏感材料石英的晶轴偏转对其产生的影响。

1.2 晶轴偏转下维间耦合公式推导

在石英力传感器中,一般应用X切族X0°切型的纵向压电效应和Y切族Y0°切型的剪切压电效应测力,如图3所示。不同切型晶片的布置方式由其晶体坐标系(x-y-z)表示,其敏感轴(电轴)x以红色标识。(因侧向力的测量原理相同,以Fx测量为例)。

图3 石英不同切型与测量布置方法

由图3(b)可看出,晶片上表面分别受力接地,下表面取电荷时,输出电荷与外力间关系:

X0°:Q=d11Fz

(1)

Y0°:Q=d26Fx

(2)

式中d11,d26为压电常数。假设因加工偏差等原因出现晶轴偏转,如图3(a)所示,晶体坐标系(x-y-z)绕大地静止坐标系(X-Y-Z)顺时针旋转,绕X轴旋转x,绕Y轴旋转y,绕Z轴旋转z,变换矩阵R为

(3)

由于电荷密度、应力和压电矩阵d三者的张量阶数不同,为求得新坐标系下压电常数矩阵d′,按照张量变换关系,需乘以张量变换矩阵N,即:

d′=RdNT

(4)

式(4)有大量的三角函数高次项,计算与分析较难。根据石英晶轴偏转角在工程上很小,采用泰勒近似方法,同时略去3次及以上高次项后,晶轴偏转下部分新压电系数:

d′11=(1-3z2)d11

(5)

d′15=(-2y+4xz)d11+xyd14

(6)

d′16=(-4xy+6z)d11+(y+xz)d14

(7)

d′22=-3zd11

(8)

d′24=(2y-4xz)d11+(-xy)d14

(9)

d′26=(-2+6z2)d11+(x-yz)d14

(10)

与原始压电系数矩阵相比,含晶轴偏转的压电系数矩阵中部分原本为0的系数不再为0,增加了新的力-电转换关系,形成本质耦合干扰,此时图3(b)中石英输出电荷与外力间关系:

X0°:Q′=d′11Fz+d′15Fy+d′16Fx

(11)

Y0°:Q′=-d′22Fz+d′24Fy+d′26Fx

(12)

式(5)～(12)建立了石英晶轴偏角与受力输出电荷的关系,也是含有晶轴偏转下石英力传感器耦合输出的基本原理。由于采用了近似,下面将其与有限元仿真得出的结果比对,验证其精度。

2 晶轴偏转仿真验证

2.1 仿真模型建立

采用COMSOL软件压电多物理场仿真,配合电路物理场采集电荷。模拟切片为内径∅8 mm、外径∅20 mm、厚1 mm的环片,材料设为石英IRE1949。在环片上表面施加力并接地,下表面收集电荷进行点约束。网格划分采用扫掠,如图4所示。由图可知,最差单元质量为0.96,模型网格较好。

图4 模型网格划分

为了灵敏度计算方便,设施加力值为1 000 N。按照图3(b)所示布置,对X0°晶片施加Fz向1 000 N,对Y0°晶片施加Fx向力为1 000 N,X0°、Y0°切型晶片电势如图5、6所示。接地端电势为0,下端电荷积累形成电势。

图5 X0°切型晶片电势

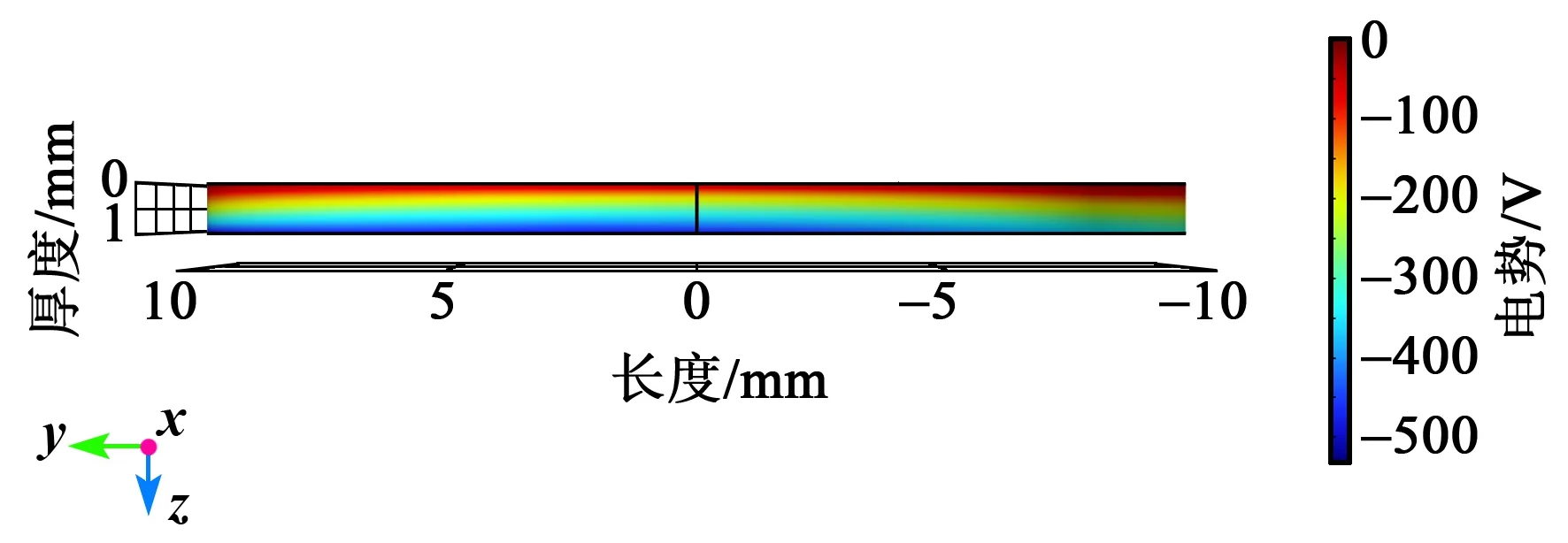
图6 Y0°切型晶片电势

将X0°晶片Fz向和Y0°晶片Fx向称为主方向,将晶片其他向称为干扰方向。按图3(b)中所示外力方向施力,QFx为受Fx力输出电荷,QFy为受Fy力输出电荷,QFz为受Fz力输出电荷,仿真结果如表1所示。由表可知,主方向灵敏度分别为-2.307 pC/N和4.614 pC/N,与压电常数d11和d26相符,其他方向耦合输出极小,精度较高。

表1 理想无晶轴偏转石英受力输出

2.2 公式验证

使用极化坐标系旋转模拟晶轴偏转,如下:

1) 通过软件将极化坐标系绕单轴旋转,偏角为-0.2～0.2 rad中均匀取10个点。

2) 不同轴、不同偏角下,对两种晶片沿图3(b)外力坐标系3方向各施加1 000 N,记录电荷。

3) 将偏角和力值代入式(5)～(12)比较计算电荷与仿真电荷。

首先分析两种晶片主方向输出随偏角变化,如图7所示。随着偏角变化,二种晶片主方向输出电荷发生变化,灵敏度有增有减。

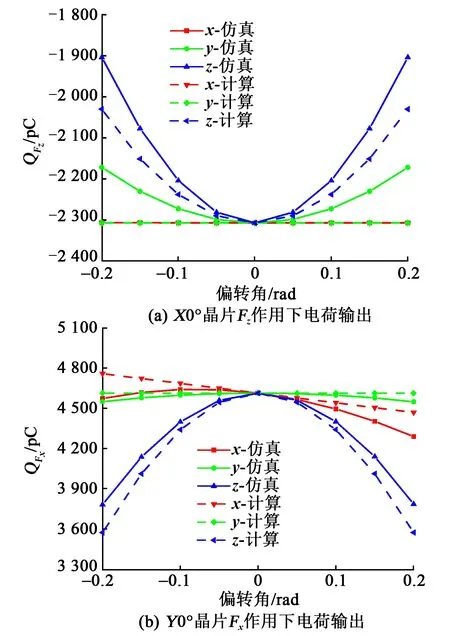
图7 两种晶片主方向电荷输出

图8、9分别为不同干扰方向输出随偏角的变化情况。由图可看出,随着偏角变化,两种晶片在干扰方向具有了灵敏度,且偏角越大,输出电荷越大,干扰灵敏度越大。

图8 X0°晶片干扰方向电荷输出

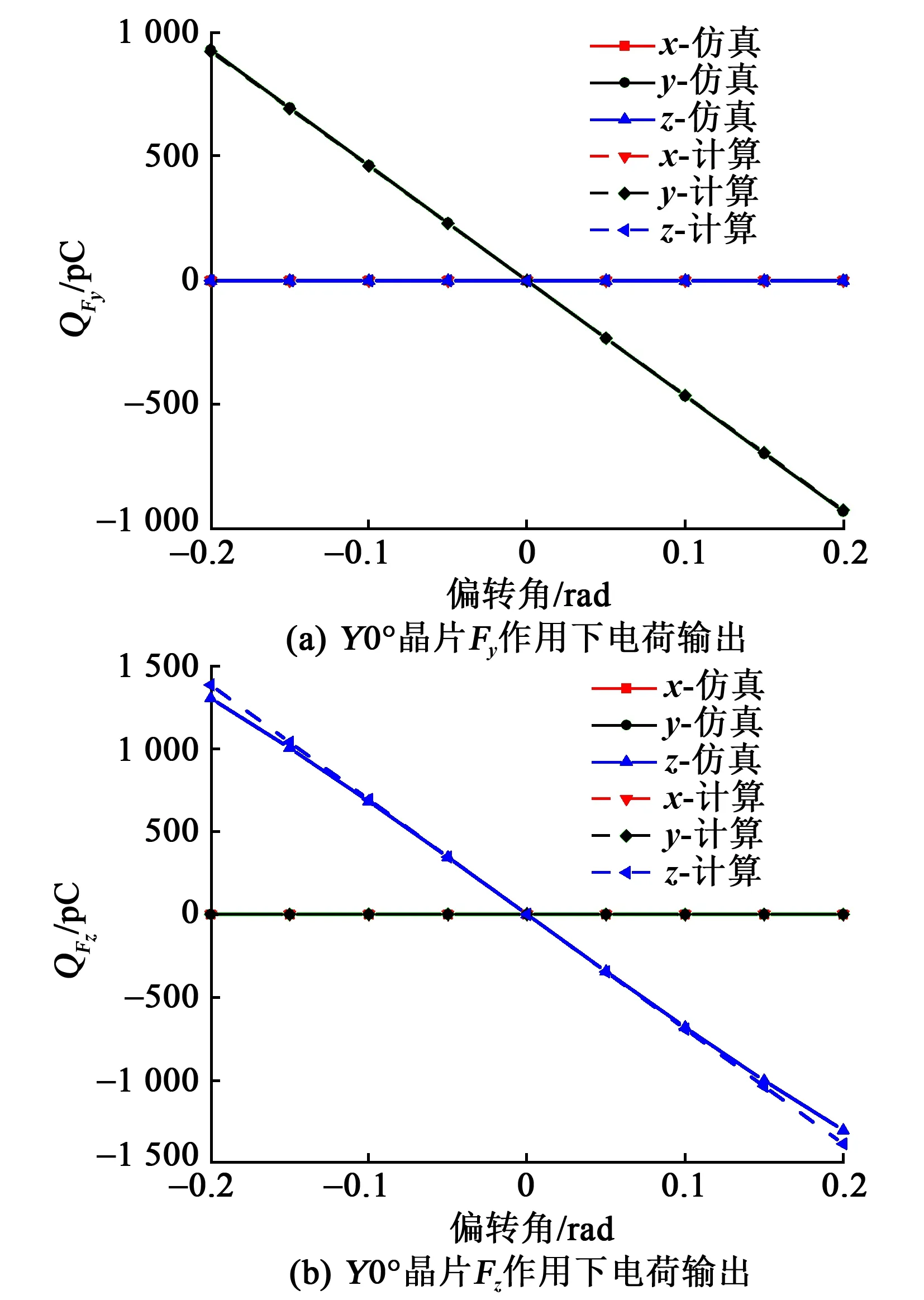
图9 Y0°晶片干扰方向电荷输出

比较结果可得,偏角在[-0.2,0.2] rad内,简化公式在单轴偏角下所得曲线与仿真接近,但仍有偏差较大的情况。偏角区间中取±0.10、±0.15、±0.20共6个点,计算式(5)～(12)与仿真结果的相对偏差,比较公式精度结果如表2所示。

表2 简化公式与仿真相对偏差

由表2可知,大部分偏角情况下偏差在2%～6%,但在某些情况下,偏差超过10%,为保证精度在5%内,将公式使用范围定为[-0.1,0.1] rad。

3 晶轴偏角容差范围计算

为了增大灵敏度和方便接地,实际使用两片相同切型的石英对装形成晶组,这会使晶轴偏转引发的维间耦合叠加或抵消。据式(5)～(12)可求出两种切型晶组的主向灵敏度与耦合灵敏度参数。

作为传感器的敏感材料,耦合灵敏度应该越小越好。目前还无针对敏感材料的耦合灵敏度标准,这里定为≤1%。对于测量Fz的X0°晶组,其对Fx、Fy的耦合灵敏度应小于Fz灵敏度的1%,即

|εFx|≤0.01|SFz|

(13)

|εFy|≤0.01|SFz|

(14)

对于测量Fx的Y0°晶组,其对Fz和Fy的耦合灵敏度应小于Fx灵敏度的1%,即:

|εFz|≤0.01|SFx|

(15)

|εFy|≤0.01|SFx|

(16)

将式(5)～(12)计算的晶组灵敏度代入式(13)～(16)可得两种切型的偏转容差不等式组。考虑代入后为三元二次不等式,含有绝对值,计算较复杂,因此,采用COMSOL内置优化算法计算。优化一般包括设计变量、约束条件和目标函数3部分。设计变量为三轴偏转角x、y、z。

约束条件包括变量取值范围和耦合灵敏度限制,根据第2节分析,为保证计算精度,偏角取值范围为[-0.1,0.1] rad。耦合灵敏度限制为式(13)～(16)。

设目标函数为

θ=|x|+|y|+|z|

(17)

式(17)代表晶轴三轴偏转容差。

在约束条件下,求解目标函数式(17)最大值,即最大偏转允许范围。选择多种算法(包括Nelder-Mead单纯形法、坐标搜索法、BOBYQA信赖域法)求解,计算轨迹如图10、11所示。计算结果如表3所示。

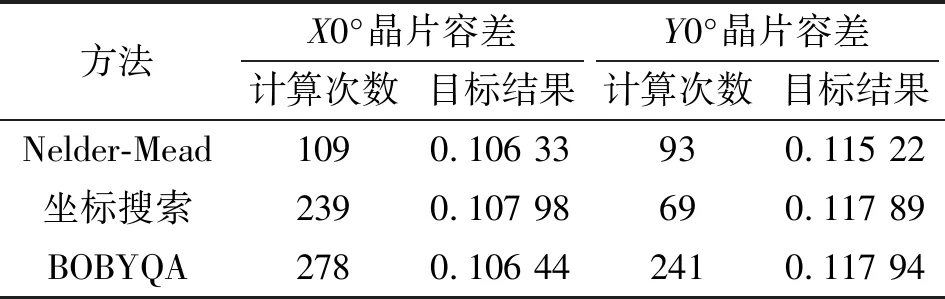
表3 容差求解结果

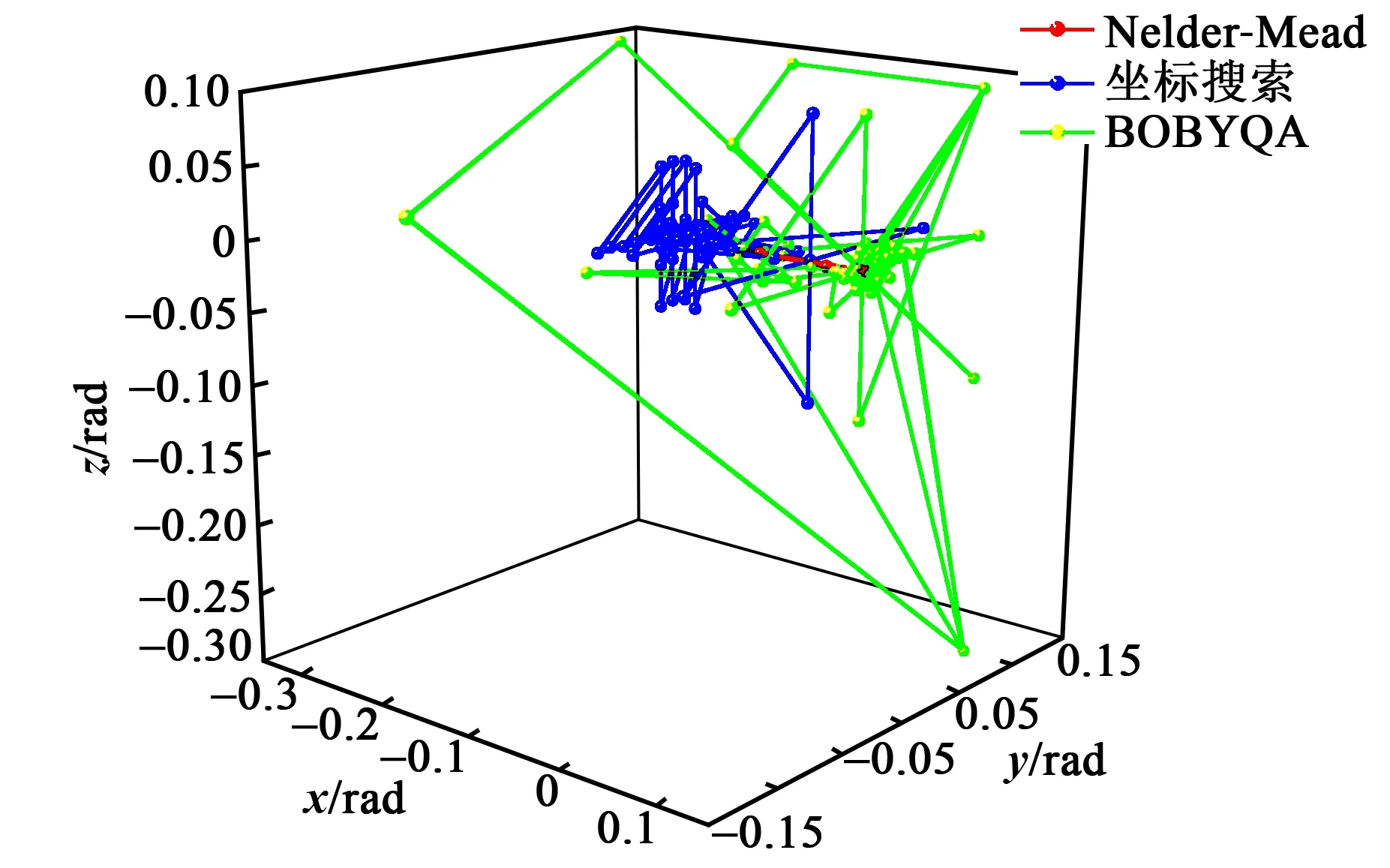
图10 X0°晶组优化计算轨迹

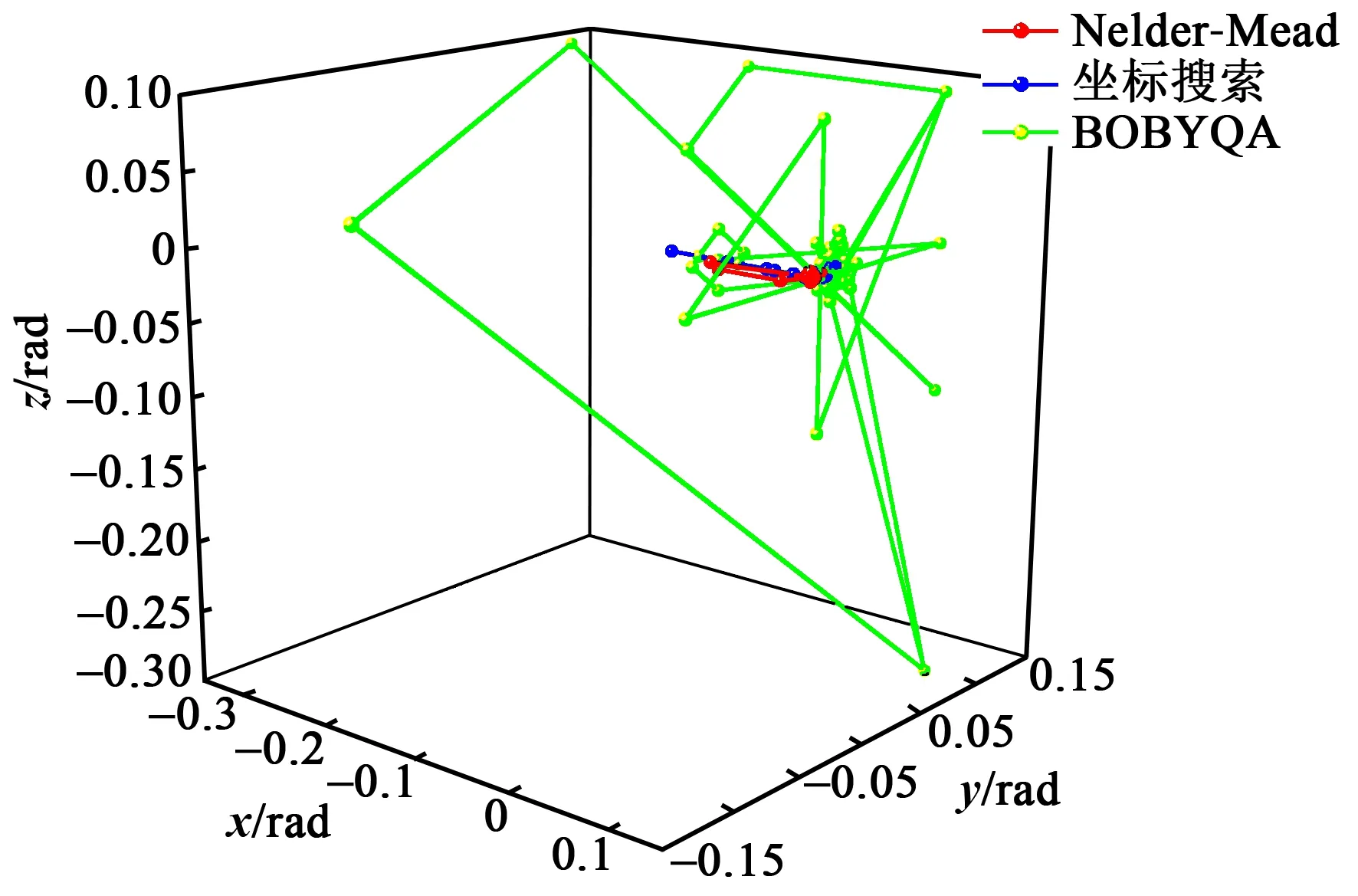
图11 Y0°晶组优化计算轨迹

即要使石英敏感材料引入的耦合灵敏度≤1%,其三轴偏转角x、y、z应满足:

θ=|x|+|y|+|z|≤0.106(rad)

(18)

4 结束语

本文以压电石英力传感器为研究对象,针对晶轴偏转建立了其与传感器维间耦合关系公式。补充了现有压电传感器精度研究体系。有限元仿真表明,该公式在偏角为[-0.1, 0.1]rad内精度较好。结果显示,晶轴偏转可影响主向灵敏度,同时引起较大的耦合灵敏度,应予以控制。从耦合灵敏度≤1%角度出发,基于优化算法,给出应满足的角度容差范围,偏转角绝对值的和应不超过0.106 rad。

晶轴偏转产生的现象需精密设备才能验证。本文的推导、简化、仿真与验证过程适用于其他压电材料传感器。在设计前期可从敏感材料方面分析其工艺要求,控制制造成本,进而削弱力传感器维间耦合或多轴加速度计串扰,提高测量精度。