基于蚁群优化特征选择的辐射源个体识别
顾楚梅,曹建军,魏志虎,徐雨芯
(1. 南京信息工程大学计算机与软件学院,江苏 南京210044;2. 国防科技大学第六十三研究所,江苏 南京210007)
1 引言
辐射源个体识别(Specific Emitter Identification,SEI)利用辐射源信号中提取的有关各种设备的本质差异特征来实现对不同辐射源个体的识别。在无线通信安全领域,通信网络非法攻击的现象日益严重,通过预处理、提取入侵的辐射源特征并进行分类识别,为保证通信网络安全提供了支持。在军事应用上,为防止敌方的通信设备对我方进行干扰,可利用辐射源个体识别技术来识别敌方设备并进行一定干预,具有重要的战略战术意义[1]。
为识别辐射源个体,需要对来源于辐射源设备的信号进行预处理、特征提取和分类识别[2]。而通常特征提取后得到的辐射源信号特征维数较大,且常含有不相关或冗余特征,这将会降低分类器的分类性能。利用特征选择(Feature Selection,FS)的降维功能可以很好地解决这一问题[3]。
特征选择是一种数据预处理方法,使用某种评价标准从原始搜索空间中选择特征子集。要求在特征子集尽可能小的情况下准确识别目标。
特征选择模型通常采用两类目标函数:某种集合距离函数和分类器的分类测试结果。集合距离函数计算复杂度较低但分类正确率也相对较低;分类器的分类测试结果针对性强,分类正确率较高但这种方法的计算复杂度也相对较高[4]。
特征选择的主要困难为搜索空间随特征数的增加呈现指数级增长,如何采取高效的搜索策略往往决定了特征选择问题能否有效求解。传统的特征子集搜索策略包括:顺序向前搜索、顺序向后搜索、顺序向前浮动搜索和顺序向后浮动搜索[5]。演化计算技术具有良好的全局搜索能力,与传统的搜索策略相比,其主要优势为不需要领域知识和对搜索空间做任何假设,除此以外,其基于种群机制的特点能够在一次运行中产生多种结果,更适合用来进行特征选择以确保能同时满足较小特征子集个数和较大分类正确率的目标。一些基于演化计算的特征选择算法有蚁群算法、粒子群算法和遗传算法等[6]。
蚁群优化(Ant Colony Optimization,ACO)算法是受自然界蚂蚁觅食行为启发而广泛应用的一种启发式算法,该算法的优点主要是信息正反馈、较强鲁棒性及并行分布式计算等[7]。最早被用于解决旅行商问题,随后其它组合优化问题如背包问题和特征选择问题也能运用蚁群算法得到解决[8]。文献[9]提出了一种利用ACO求解特征子集的方法,利用特征向量图来搜索特征子集。但该方法较易陷入局部最优解且稳定性不高。文献[10]提出一种基于改进蚁群求解特征子集的入侵检测方法,对进行预处理后的数据集根据信息熵理论初步提取特征,用改进蚁群算法进一步求解特征子集。但该算法的训练时间并未显著减少。文献[11]提出了一种融合蚁群算法和随机森林的特征选择方法,将随机森林的重要度评分作为蚁群算法的启发式信息,但该算法仅对ACO的启发式信息进行优化,创新性较低。文献[12]提出了一种基于二元全连通图的最小冗余最大相关蚁群算法,特征节点通过访问概率随机访问,子节点通过先验知识选择,该方法能有效降低特征选择的时间开销。文献[13]提出了一种基于图的蚂蚁系统(Graph-Based Ant System,GBAS),该算法基于构造图提出了等效路径的概念,将问题的无序信息和有向图的路径相结合,实现了将无序信息转化为有序信息,该方法提高了蚁群算法的性能。
综上,为解决辐射源信号维数较大问题,提出了一种基于蚁群优化特征选择的辐射源个体识别方法。给出以最大分类正确率和最小特征子集规模为目标的特征选择数学模型;特征选择的目标函数使用分类器的分类正确率;搜索算法使用蚁群优化算法。实验表明相比于传统的特征子集搜索策略,提出的方法能在降低特征数目的同时提高辐射源信号的分类正确率。
2 辐射源信号的蚁群优化特征选择
2.1 特征选择的数学模型
为实现对不同辐射源个体的识别,首先利用相关信号分析技术[14],对采集信号进行预处理并从中提取出一定数量的特征,这些提取出的特征可以构造一个特征集set={t|t=1, 2,…,T,T∈N},set集中特征对应的特征向量记为V。现有W类的Y个特征向量样本,记Vwyt,w=1, 2,…,W,y=1, 2,…,Y,t=1, 2,…,T,为第w类中第y个样本向量的第t个特征值。
特征选择的过程即根据上述特征向量样本从集合set中选择基数为q的一个特征子集subsetq,使该子集对应的特征向量样本满足某种目标函数。
根据所研究的问题即辐射源信号个体识别问题的本质是分类问题,特征选择和分类器的性能相关联。因此直接使用分类器的分类正确率作为特征选择的目标函数。实验部分中的数据集为从两个电台发出的辐射源信号数据,旨在通过辐射源个体识别技术识别两个电台进而分析电台的性质、属性和危险等级等,本质上是一个二分类问题,故可以采用支持向量机(Support Vector Machine,SVM)作为分类器。
对使用分类器的分类正确率作为目标函数的特征选择算法,特征选择问题可以描述为:从集合set中根据目标函数得到一个基数为q的特征子集subsetq,subsetq所含特征对应的特征向量样本分类正确率P最高。数学模型为
(1)
minq
(2)
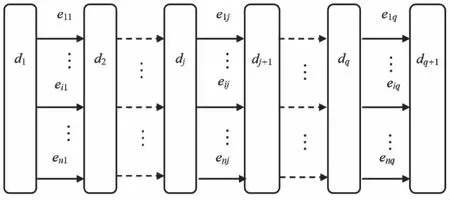
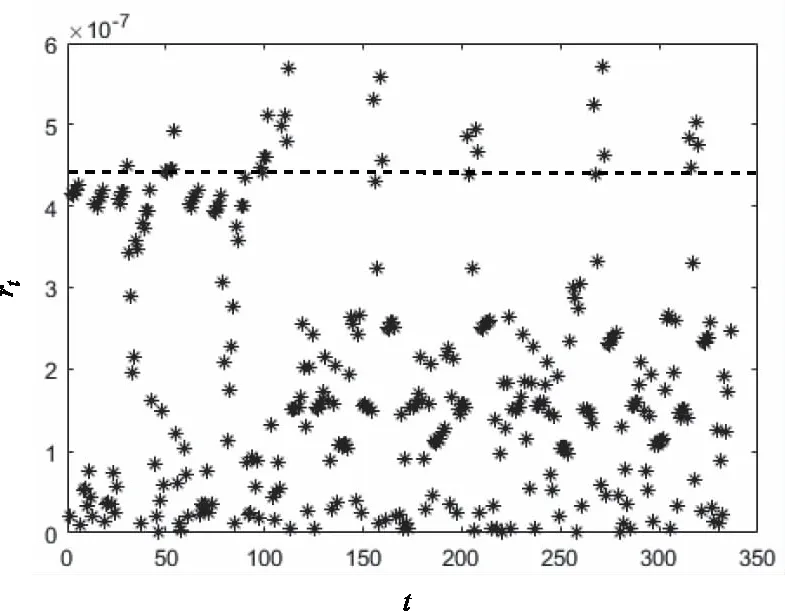
s.t.|subsetq|=q,1≤q (3) 2.2.1 蚁群优化 以最大分类正确率和最小特征子集规模作为优化目标,引用文献[13]中的GBAS算法求解。 引入GBAS,根据辐射源信号特征选择问题构造有向图,如图1所示。 图1 子集问题构造图的有向图 上图辐射源信号特征子集问题构造图的有向图中,有向图的边代表备选特征,路径映射为一个求得的辐射源信号特征子集。节点dk(k=1, 2,…,q+1),在d1处人为设定蚂蚁的数量为A,每只蚂蚁根据有向图边上的信息素量和启发式信息随机独立地选择从某一个节点di走到下一个节点dj,此问题中,即随机地选择下一个信号数据。其中n为特征总数(特征提取后得到的辐射源信号特征总数),q为蚂蚁在一次搜索过程中找到的解的个数,eij表示蚂蚁在步骤j时选择第i个特征。 引用路径选择概率公式来实现图1中蚂蚁的路径构建,如(4)式所示。 (4) 式(4)中τij(s)为s(s=1, 2,…)时刻边eij上的信息素量,初始化信息素量τij(0)=0;用禁忌表tabua(a=1, 2,…,A)记录第a只蚂蚁走过的边;α,β分别为信息素量和启发式因子的重要程度;ηi是启发式因子且为内部信息,表示选择第i个元素的期望程度,视情况而定具体表达式。 针对本文研究的信号数据的特点,启发式因子ηi的公式如下。 (5) 信息素量随迭代次数变化,一次迭代完成后,按照一定的规则对信息素进行更新,信息素更新公式如下 (6) 式中ρ为信息素挥发系数;tabus为s时刻选择的特征路径;φ’(tabus)为要进行信息素增强路径的目标函数值,为信息素增量公式;Q为常数(根据ρ值确定,调节信息素增量的大小)。 2.2.2 蚁群算法流程图 基于蚁群优化特征选择的辐射源个体识别算法可以概括为:首先依据路径转移概率公式构建某条路径;然后根据目标函数即分类器的分类正确率来判断当前解是否为最优解,进而更新信息素。算法终止条件为达到设定的最大运行次数。 其流程图如图2所示。 图2 蚁群算法特征选择流程图 3.1.1 数据准备 实验在1台i7-4770 3.40GHz 4核处理器、24GB内存的电脑上运行,开发环境为Matlab R2017a。实验数据来源于两个相同型号的辐射源电台,采集环境为基本无噪声的干净环境,两个电台发出的信号数据分别在10种不同的采集状态下获得。10种采集状态下信号具体参数如表1所示。 表1 信号参数 3.1.2 预处理 为统一数据样本的数量级、增加可比性及加快算法收敛速度,采用Z-score标准归一化对特征值进行标准化[15],公式如下。 (7) Z-score标准归一化将原始的数据转换到某个范围,且不会改变原始数据排列顺序。归一化后,不同数量级的特征在数值上进行了统一,提高了分类器的正确率;最优解的寻优过程更为平缓,容易正确地收敛到最优解。 对原始I/Q采样数据取模,可得到信号的频域表达,信号I/Q两路采样可以降低采样率且保留原始信号的信息。为保证信号数据的多样性,现将实验数据扩展,分别为:取模后的信号数据、I路信号数据和Q路信号数据。然后经过信号其它预处理过程及基于集成特征提取算法,依据信号时频域的特点,对信号进行两层提升小波包分解[14]。选取12个统计量(均值、平均幅值、方根幅值、标准差、有效值、峰-峰值、波形指标、脉冲指标、峰值指标、偏斜度、峭度和峪度指标)及各频带内能量。对于求幅值后的信号数据,按组(每组4096个数据)进行特征提取,得到重构原时域信号的12个统计特征参数(1-12)、小波包分解的第二层四个节点系数的各12个特征参数(13-60)、四个单支重构信号的各12个统计特征参数(61-108)和4个标准化相对能量(109-112)。对于I路信号数据,用相同的方法得到特征113-224,对于Q路信号,得到特征225-336。构建特征集set={t|t=1, 2,…, T, T=336}。每个电台分别在每种采集状态下选取200组数据(共得到2000组数据),得到两台电台的2×2000个特征向量,选取总特征向量的3/4用来训练,1/4用来测试。 上述实验数据在无噪声的干净环境下采集得到,为模拟信号的普遍实际状态,在实验前可先将信噪比分别调整为10dB和5dB,特征提取分别得到特征集set={t|t=1, 2,…, T, T=336},再按提出的算法进行特征选择并进行实验。 将文献[5]中基于类间类内距离比的向前搜索算法选择特征子集与文中基于蚁群优化算法选择特征子集的结果进行比较。 文献[5]方法:基于类间类内距离比的向前搜索特征选择算法分别计算每类第t个特征的类间平均距离和类内平均距离,并计算第t个特征的类间类内平均距离比rt,类间类内平均距离比rt反映了特征t分类的难易程度。按照rt对特征进行排序,选取前q个rt较大的特征作为分类器的输入。用训练样本计算set中每一特征的类间类内平均距离比,得到的结果如图3所示。 图3 特征类间类内距离比 根据图3,选取前20个rt较大的特征,图中为虚线上方特征,按照rt对特征进行排序取q=1,2,3,…,20构成特征子集。分类器使用SVM(采用rbf核函数,gamma=0.4,C=100),分类正确率与特征子集基数q的关系如图4所示。 图4 特征选择算法对比 本文方法:基于蚁群优化的特征选择算法参数初始化:τij(0)=1,α=1,β=1,ρ=0.2,Q=0.02,蚂蚁数A=45,最大迭代次数Nc=200。采用SVM分类器(采用rbf核函数,gamma=0.4,C=100)。分别取q=1,2,3,…,20,为降低蚁群优化算法蚂蚁初始位置的随机性对最终结果的影响,重复实验10次取平均分类正确率,平均分类正确率与最优特征子集基数q的关系如图4所示。 根据图4,基于类间类内距离比的向前搜索算法得到的最优q值为17,分类正确率为77.2%;基于蚁群优化的辐射源信号特征选择算法得到的最优q值为14,分类正确率为85%。 当q值相同时,明显可以观察出使用基于蚁群优化的辐射源信号特征选择算法选出的特征子集比基于类间类内距离比的向前搜索算法选择特征子集的分类正确率有较高提升,说明使用提出的算法选出的特征子集更能表示电台的本质特性从而区分这两个电台,进而分析电台的危险等级,在现代数字化信息战场取得优势;随着q值的增加,使用蚁群优化算法选出的特征子集分类正确率总体上呈现出先增后减的趋势,如图中表明当q=14时,特征选择的效果最好,这也满足了算法的目标,即从规模和分类效果综合衡量选取最好的特征子集。 实验3.2中数据在基本干净无噪声的环境下采集得到,为模拟信号的实际状态,现通过添加高斯白噪声改变信噪比条件(10dB, 5dB),再进行特征提取分别得到特征集set={t|t=1, 2,…, T, T=336},分别取基数q=1,2,3,…, 20,分别使用基于类间类内距离比的向前搜索算法和基于蚁群优化的辐射源信号特征选择算法得到最优特征子集,实验结果如表2所示。 表2 不同信噪比下最大分类正确率 根据表2,当输入经过高斯白噪声处理更低信噪比数据时,提出方法的分类正确率仍普遍高于文献[5]方法的分类正确率,进一步验证了基于蚁群优化特征选择的辐射源个体识别方法优于传统的特征子集搜索方法。随着信噪比的降低,辐射源信号的分类正确率呈下降趋势,当信噪比为5dB时,分类正确率为63.4%,效果较差。在处理实际信号数据时,当噪声严重影响分类结果时,需要对辐射源信号进行预处理如降噪等来提高分类识别的效果。 本文提出了基于蚁群优化特征选择的辐射源个体识别方法,建立了辐射源信号特征选择的数学模型,并用蚁群优化算法进行求解。 1)以分类器的分类正确率作为特征选择的目标函数,同时满足最大分类正确率和最小特征子集规模的要求,建立了特征选择数学模型; 2)使用蚁群优化算法,基于子集问题的构造图,采用路径转移概率公式进行路径搜索,利用基于等效路径增强的信息素更新策略公式,求解了辐射源信号特征选择模型; 3)结果表明,相比基于类间类内距离比的向前搜索算法,提出的基于蚁群优化特征选择的辐射源个体识别方法选出的特征子集分类正确率进一步提升,性能更优,为正确分类识别辐射源个体提供了新思路。2.2 求解模型的蚁群算法设计


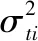


3 实验结果与分析
3.1 数据准备与预处理

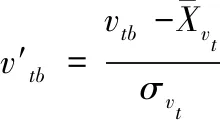

3.2 特征选择算法比较结果

3.3 不同信噪比下测试结果

4 结论

