模型数据混合驱动的水声器材防御决策方法
杨 静,黄金才,张驭龙,郭力强
(1. 国防科技大学,湖南 长沙 410073;2. 海军潜艇学院,山东 青岛 266071)
1 引言
战术决策是一个连续时间决策过程,一种通用的方式是采用基于时间步长推进仿真,将连续时间离散化。在最优决策推演、精确制导武器参数设定等战术领域[1,2]应用广泛。过程仿真的时间步长是影响仿真时间、精确程度的重要因素。在实际应用过程中,传统依赖于过程仿真的方式存在一些难以解决的困难。一是环境、态势数据的高维特性、以及水中作战环境瞬息万变,导致规划决策空间出现“维度灾难”。二是水中对抗态势演化迅速,基于仿真步长的推演过程难以简化,导致决策实时性和决策精度之间存在矛盾。
随着人工智能技术的发展,越来越多研究者将目光投向基于数据驱动的智能决策技术研究。通过数据驱动模型代替基于模型-时间步长方式的推演,可以有效缓解传统模型仿真效率难以提高问题。在一次决战过程中,对抗态势发生往往紧迫而短促,无论是攻击还是防御决策数据,快速采取有效攻防对策都是决胜的重要因素。特别是水中潜艇存在着保持隐蔽性的特殊需求,攻击、防御器材的使用不当可能导致行动无效甚至意外暴露,因此对防御决策提出了更高的可靠性要求,单纯从数据出发的学习模型其灵活性、实时性、抗风险能力等很难保证。
水中对抗、特别是水中防御问题决策属于一个严重的不均衡数据学习问题[1,2]。已经证明在近距离条件下的有效防御决策空间在整体决策空间中所占的比例非常小。如何从不均衡数据中学习一个无偏模型,一直是一个具有挑战性的任务。传统的不均衡学习基于随机假设条件设计重采样和重新设计权重的机制。但是经常会导致执行效率不稳定,适应性较差,而且一旦任务复杂、初始假设不成立,计算代价极高甚至结果发散等问题。
本文的贡献在于:一是以水中对抗环境下,潜艇使用水声器材防御来袭鱼雷的决策问题为例,提出一种全新的数据和模型混合驱动的仿真决策方法,以同时满足决策效率和抗风险能力等需求。二是提出了一个新的集成不均衡学习框架,可以在训练集上每次迭代的时候自适应的选择采样策略,从而得到不同的分类器,并得到集成模型。文中的学习框架不同于已有的基于元学习的不均衡学习策略,通过在元采样基础上独立训练一个元分类器的方法,将模型训练和元训练步骤解耦合。这使得文中的策略可以在大部分学习模型上兼容,并且,元采样器也可以很好的适应新的任务。
2 水声器材防御模型
本节将首先对决策模型及其仿真过程进行描述。
2.1 防御决策问题的描述
假设1:潜艇鱼雷报警态势用鱼雷到潜艇的距离D和鱼雷所处的潜艇舷角X表示。以潜艇为坐标原点,潜艇当前运动方向为0度航向(以正北方向表示);
假设2:预设当前来袭鱼雷正按照有利射击提前角的方向行进,如图1所示。

图1 潜艇防御鱼雷态势图
潜艇使用水声器材防御鱼雷的具体过程为:
i)潜艇接到鱼雷报警后,以速度Vsub,转向半径Rsub开始做转向Hb角度的规避,并同时发射一枚诱饵,以诱导来袭鱼雷并为我转向规避争取时间;
ii)发射诱饵的速度为vbait,其固有转向半径为rbait,诱饵出水后首先转向αb1角度,然后直航tb1时间,再转向αb2角度,然后再直航至航程终了。其中转向过程仍以其转向半径做匀速圆周运动,直航时为匀速直线运动。
iii)来袭鱼雷速度为vtor(vtor>vbait>vsub)做匀速直线航行搜索,其初始航向为当前态势下鱼雷与潜艇相遇三角形对应方向Htor,其计算方法如式(1),鱼雷在未发现目标时做直线运动,一旦目标进入其探测扇面,则转向追击目标。

(1)
在模拟一次仿真的过程中,每个实体都按照有限状态机模型运动(如图2)。决策的目的是在整个状态空间内,找到最优的潜艇使用鱼雷防御方案的四元组(Hb,αb1,tb1,αb2),其中Hb,αb1,tb1,αb2分别为潜艇转向角,诱饵的第一次转向角、第一段直航时间和第二次转向角。

图2 使用水声器材防御鱼雷过程有限状态机
2.2 仿真优化与复杂度分析
2.2.1 价值函数
决策四元组的状态空间内,每次仿真过程,潜艇与鱼雷探测扇面的最小距离可以作为价值函数,定义为

(2)
其中,C为鱼雷搜索扇面,函数Dis(x,y,C)为潜艇当前所在坐标(x,y)到鱼雷搜索扇面C的最小距离,求得一次仿真的最小距离算法如下所示。
算法1:OneSim(D,X,Δt,Hb,αb1,tb1,αb2,init[11])
初始化:潜艇状态机=1;潜艇参数;鱼雷状态机=1;
鱼雷参数;诱饵状态机=1;诱饵参数;
for Δt in total_Time:
潜艇到扇面D=f(Dis(x,y,C));
诱饵到扇面D_bait=f(Dis(x,y,C));
诱饵到识别扇面D_bait2=f(Dis(x,y,C));;
if D if Dmin<0 do return Dmin; if StateS==1 do 潜艇转向 else: 潜艇直航 ∥StateS=2; if StateB==1 do 诱饵准备 elseif StateB==2 do 诱饵转向 elseif StateB==3‖StateB==5 do诱饵直航 elseif StateB==4 do 诱饵转向 else do State B=6 if 诱饵达到最大航程do State B=6 if StateT==1 do鱼雷直航 else鱼雷尾追目标∥StateT=2 end for return Dmin 一次搜索过程的决策粒度取决于搜索的Δt,如果仿真步长过大,则可能会忽略重要的极小值点,造成决策失误。在一次仿真过程中,每个实体按照触发条件进行基于有限状态机的运动模拟,因此,一次仿真过程本身的复杂性决定了其无法从算法上进一步并行优化。 算法2:MTaskSim() 初始化:态势参数(11维) fori1 in range(1,N): for i2 in range(1,N): fori3 in range(1,N): for i4 in range(1,N): Dmin=OneSim(D,X,Δt, Hb[i1],αb1[i2],tb1[i3],αb2[i4],init[11]); if DminYou>Dmin DminYou=Dmin; end if end for end for end for end for 而整个仿真决策的过程中,通过对四元组在整个状态空间的组合搜索,找到所有最小值Dmin中的极大值: Dminyou=max(Dmini),i=1,…,n4 (3) 其中,n是决策四元组(Hb,αb1,tb1,αb2)的搜索粒度,四元组的搜索空间为 Hb⊆[-π,π],αb1⊆[-π,π], tb1⊆[0,Lbait/vbait],αb2⊆[-π,π] (4) 因此,最终决策组合的搜索空间为O(n4),然而考虑到一次仿真本身需要计算M个仿真步长,仿真的时长约为鱼雷整个航程段,以仿真鱼雷航行20分钟、选取步长1s为例(对于连续事件仿真,该仿真步长往往并不能满足决策精度的要求,真实环境下往往需要时间步长0.1s甚至更短),则需要计算超过 1000次复杂度为O(n4)的仿真计算,一次真实的对抗过程,往往3-5分钟就结束了,而基于模型在状态空间搜索的方式求解最优决策往往需要耗时超过5分钟,即使通过并行手段对搜索空间进行并行化可以实现103的优化(即本文简化参数条件下,实现5分钟/103=0.3秒一次仿真,这是加速的极限情况,达到103加速意味着需要多达1000核的计算资源),但由于本模型假设输入参数均为确定值,真实情况还需要考虑目标的方位、速度、航向的误差散布,即使不确定变量仅多出三个,对每种变量的散布选取100个样本用于统计结果,则计算量也将增加0.3s×1003≈83hour,因此,通过分析可以得出结论:一次战术仿真过程,随着输入态势参数的增加,仅考虑并行优化方法是无法满足决策实时性要求的。因此,本文提出一种新的基于模型与数据混合驱动的决策方法,其主要框架如图3所示。 图3 数据与模型混合驱动决策框架 图5 随机3组不均衡数据迭代训练中的AUCPRC准确率 如图3所示,右侧是传统仿真过程,左侧是基于仿真模型的集成学习网络。通过对该态势下的仿真数据分析发现,有效决策存四元组存在一个决策边界,在近距离遇敌防御条件下,整个决策空间中有效决策样本仅占极小的比例,只有当Dmin值大于0时,该决策策略才可以实现防御,因此本文通过对决策数据和Dmin取值正负的对应关系,训练了一个二分类的集成学习网络,考虑当近距离遇袭条件下,数据的不均衡IR极高(达到26以上)的情况,为了获得更高的决策效率和准确度,本文采用了如左图所示的基于元学习的集成学习模型(在第3部分详述),再将决策网络与仿真相结合,首先通过仿真确定样本空间,将仿真数据样本交给集成学习网络进行预测,再从预测出的决策边界内寻找最优解,同时,为了确保决策边界划分的准确性能够适应不同态势参数的状态,在预测模型的同时,将会同时对决策边界附近的样本进行仿真比对,如果模型预测结果与仿真结果不符,则将该数据加入权重数据库,增大边界样本学习模型的影响,从而实现决策模型的动态自适应。 考虑到问题的特殊性,采用水声器材防御通常是在近距离遇袭条件下,为了争取时间而采用的策略,当距离较近时,通过对数据分析(详见第4部分),以及对决策四元组与安全余量Dmin的相关性分析,可以看到决策状态样本离散但集中在特定空间,仅有少量特定样本会出现决策边界模糊的情况,因此,在防御仿真前,首先通过集成学习对不均衡数据做有效的判断,仅对Dmin取值大于0的情况进行仿真,可以极大提高仿真决策的效率,同时又能保证决策的可靠性。 在数据驱动模型中,关键在于解决对于Dmin取值是否大于0的判断,属于二元不平衡分类问题,数据集中只存在两个类别:少数类,即本文中的属于决策空间内的样本数量较少的类;多数类,即样本数量相对较多的类别。本文用D来表示全部训练样本的集合,其中,每一个样本用(X,y)表示,标签y∈{0, 1}。在二分类条件下,y取值为1代表该样本属于正类(少数类),为0则代表该样本属于负类(多数类)。即: 少数类集合:P={(x,y)|y=1},(x,y)∈D 多数类集合:N={(x,y)|y=0},(x,y)∈D 其中:P∩N=∅,P∪N=D 本文采用文献[1]的定义,对于(高度)不平衡的数据集,在|N|≫|P|情况下,采用不平衡比IR(Imbalance Ratio)为多数类样本数量与少数类样本数量的比值 IR=|N|/|P| (5) 对于不平衡数据,分类正确率很难有效表示分类器的效果,因此数据模型采用的评价指标为AUC-PRC。AUC(Area Under Curve,曲线下面积)采用ROC下面的面积,可以用于衡量分类器的优劣。另外,考虑到数据的极端不平衡特性,还结合准确召回率曲线PRC(Precision Recall Curve,准确召回率曲线),在负样本的数量远远大于正样本数量的情况下, PRC更能有效衡量检测器的好坏,因此,本文引用AUC-PRC作为评价指标。 考虑到过去对于不均衡数据的处理方法主要从两个方面:一是从数据层面,通过重采样[5]或者欠采样[6]方法,以提高学习过程中样本的不均衡比例;二是从模型的角度考虑,采用集成学习[4]的思想,通过多个弱分类器加权的方式代替单一分类器,以提高对于不均衡样本学习的鲁棒性。数据采样和多分类器都是为了能够从不平衡数据中(特别是少量样本中)学习一个无偏模型。然而,多个弱分类器采用随机策略对数据进行分类,因此容易陷入局部极值,且对分类器的数据设计要求较高。 因此,本文考虑采用元学习的策略,通过对分类器的权重进行先验性的调整,构建一个元学习框架,具体的思想是:直接通过仿真数据样本学习一个参数化的采样策略,代替过去集成模型的随机假设策略。框架包括三个部分,元采样、集成学习和元训练。 3.2.1 元采样方法 本文首先引入文献[4]中的“元状态”思想,希望可以找到一种对集成学习训练过程的信息有效的任务表示,从而提供有效的元采样信息。采用“梯度/硬度”分布的概念,引入了对训练样本和验证误差的直方图分布作为集成训练系统的元状态。 具体的做法是:把样本集的先验信息作为元采样的输入,给多数类的每个样本设计一个加权,将计算得到的权重作为每个样本前面的系数。对于每个数据样本集D,其权重u定义为:μ~gμ,σ(μ|D),其中gμ,σ为高斯方程用于衡量数据样本的分类误差,定义为 (6) 则对于样本集D,假设正样本比例(少数类为P,多数类为N,其D=P∪N中,对于每个(xi,yi)∈N,则其权重计算为 (7) 令N′=w·N,每次采样得到|N′|=|P|,并以子集D′=N′∪P作为每次元采样的数据集。 3.2.2 集成学习训练 基于一个采用元采样策略得到的数据样本,可以迭代的训练一个基分类器。假设采取k次迭代得到的分类器结果作为最终分类结果。则在第t次迭代过程中,将元采样得到的数据集D′划分为训练集DT和验证集Dv。对于分类器Γt(x),分类误差e可以定义为分类器Γt(x)与其真实标签之间的差,即|Γt(x)-y|,通过下方式(8)进行计算。 iD=|x,y|i-1b|≤|Γt(x)-y|≤ib||D|,(x,y)∈D (8) 其中i∈[1,b],然后,可以将训练集和测试集的误差分布向量进行拼接,就可以得到一个元状态 s=[Dt:Dv]∈R2b (9) 然后,按照元采样的思想,将分类误差e作为新的采样依据,令 (10) 作为更新权重,这个过程重复迭代k次,最后得到的结果作为最终分类结果。分析可知:误差分布直方图可以直观的表示出分类器对于数据的分类能力,本文考虑b=2的情况,其中分类准确率为1D,分类错误率2D。而当b>2时,就代表在分布的“无争议”样本(误差接近0)和“有争议”样本(误差接近于1)之间取了更为细致的粒度,因此,本模型未来也可以对多分类问题如何使用元信息提供借鉴。另外,由于同时考虑训练集和验证集,元状态可以通过当前集成模型的偏差提供一个元采样器,用于辅助决策。 3.2.3 元训练 元采样的目的是通过多次迭代选择训练数据的方式优化决策效率,它基于当前样本状态s(式(9))作为训练输入,通过高斯方程的输出参数u来决定每个样本的采样概率。元分类器的目的是通过当前的状态st、动作u得到新的状态st+1,并通过多次迭代在效率优化的条件下,通过减少差分优化训练过程。这一过程与强化学习类似: 采用基于强化学习的设定,基于马尔可夫决策过程(MDP)的四要素(SApr)可以定义为:状态空间S,动作空间A:[0,1]都是连续的。而状态转移概率p:S×S×A代表的是下一个状态st+1在当前状态st和当前动作A条件下的概率密度。在每次迭代中,分别训练k个分类器,并形成k个集成分类器F。给定一个性能度量函数P(F,D),奖赏r定义为r=P(Γt+1,D)-P(Γt,D)。则元分类器的优化目标变成了集成分类器的性能。 在不同初始态势条件下生成了以安全距离为判定依据生成了大量仿真数据样本。随着来袭鱼雷与我相对距离靠近,数据样本的不均衡比例大幅提高(在其它态势参数不变情况下,相对距离D从3海里缩短到2.7海里,相同时间步长的810000条数据中,不均衡数据比例从2.6提高到了29.4。这也从一个侧面说明,对于来袭高速武器防御,越早采取有效策略,防御的成功概率越大,但对于决策时间的要求也越高。考虑相对极端条件下的快速决策,本文的后续实验采用D=2.7条件下的,相对弦角X在区间[-π,π]内取30个区间值,每个值对应生成81万条数据,采用批量为10(batchsize),对30个区间采样的8.1万条数据进行组合,构成10个样本集,每个样本集大小为243万(30×8.1万)。总数据样本IR约为29.4,单独取出的10个数据样本集不均衡比例范围为为21.7-30.9之间,可以认为抽样数据基本满足总数据样本特征分布。 通过数据处理,将Dmin>0情况的flag为1,其余情况flag为0,得到数据总分布,和mini-batch分布分别如下图a、b所示。 通过对上述仿真模型进行分析,一次仿真的最小安全距离可以作为判定决策四元组Hb,αb1,tb1,αb2是否能够有效防御来袭鱼雷的依据,通过对状态空间内所有四元组组合的分析,发现可防御四元组仅占总体决策空间的极小一部分,然而,传统的基于仿真方法需要遍历所有状态空间以寻求最优,即使采用及早停止的相关策略,仍然无法避免在所有决策空间上的遍历(算法1的OneSim过程),极大影响决策性能,因此,考虑采用数据与模型混合驱动的方式,利用数据学习模型实现两个任务:一是针对当前态势,预测状态空间的范围;二是在对状态空间的最小安全距离Dmin给出合理的回归分析,实现高可靠度的预测。 在81万条数据中通过等间隔方式划分为10个子集,每个子集数据81000条。再从中随机选取3个样本集分别用于训练、验证和测试,重复这个过程7次得到的模型用于最终数据与模型混合驱动仿真模型,其中,数据训练的样本准确率采用AUCPRC准则进行评估,下图是随机选取3组不均衡数据比例为22.6,22.8,23.9的81000数据子集作为训练集、验证集、测试集时,迭代训练过程中的AUCPRC准确率。数据驱动模型在单个训练集上极容易过拟合,但是在验证集、测试集上都可以达到98%以上的预测准确率,考虑到预测的目的是缩小决策空间,对于一个仿真模型,对其决策空间预测准确率达到98%,并在该决策空间内进一步搜索决策最优解,可以认为是可行的。 尤其是当这种决策可以极大程度提高模型运算效率的情况下,下表给出了三种态势下,模型仿真与使用文中的元训练模型预测的时间和决策方案。 态势说明:态势1,距离D取3.2海里,样本不均衡比例IR=1.6;决策四元组(-3.1416,-1.1916,0.0502,-0.3245);态势2,距离D取2.7海里,样本不均衡比例IR=22.7;态势3,距离D取2.4海里,样本不均衡比例IR=59;决策方案是最小安全距离Dmin的最大值所对应的方案四元组,以及对应的Dmin取值。 混合模型的决策时间包括两部分:一是7轮样本训练的总耗时,二是决策模型仿真时长,以两部分加和作为总决策时长。 可以看出,虽然混合模型并未得到最优解对应的决策方案,但是仍在可行域内得到了相对较优的决策方案,且计算效率大大提升。从D为3.2海里到2.4海里,随着时间流逝,可行决策空间大幅下降,这也从另一方面表明水中防御态势情况紧急,快速决策对于紧急条件具有重大意义。采用混合决策模型,运行时间分别下降了63、16、8.8倍,越早决策,可行空间越大,因此从整体上看,模型与数据混合驱动方法可以很好的提高决策效率。 首先对元集成学习的方法和其它6种有代表性的不均衡集成学习方法进行了对比。包括2种欠采样策略(ORG、RUSBoost[9])和4种过采样不均衡集成学习方法(SMOTE[7]、 BorderSMOTE[8]、SMOTEENN、SMOTEomek)。采用的都是同一个数据样本(从30*10个样本中选出的不均衡比例最高的81万条数据),测试其分类效率和准确性。对于不同的基分类器,比如K近邻、高斯贝叶斯(GNB)、决策树(DT)、自适应梯度(AdaBoost)和梯度下降(GBM),通过不同的采样策略与这些分类器进行结合,记录了不同方法的决策精度和执行时间(执行时间都是10次运算取平均值),如下表1。利用AUCRPC分数来记录不同集成学习算法的效果,并对所有方法AUC和运行时间做了对比。结果表明,文中的元训练方法在几个不均衡比例很高的数据样本集上在精度较高条件下,计算时间也更短。 表2 不同集成学习方法分类效率和准确性对比 本文主要关注的是战术决策问题,传统的战略决策的仿真常用的方法是基于决策状态空间的搜索。然而这种搜索即使有提前终止策略,由于决策过程是连续的,离散化仿真的时间步长是很难进行优化的,特别当水中对抗条件下,实体的数据探测、感知往往就在分秒之间。 本文通过数据与模型混合驱动的方式,可以在决策初始通过集成学习方法,利用仿真样本学习缩小决策空间,从而提高最终模型搜索的精度。然而,水中防御是一个相对复杂的战术对抗过程,未来,一方面还将从模型上考虑敌我双方的博弈与对抗;另一方面,还需要通过扩大样本规模、探究当高维状态空间数据存在更多种变化时,模型的迁移、泛化能力。随着高维环境数据的变化,防御模型中的决策状态空间也会发生剧烈的变化。因此,未来这种数据模型混合驱动方式的模型可迁移性和适用场景问题是我们需要特别考虑的。2.2 复杂度分析


2.3 基于模型与数据混合驱动的决策方法
3 基于模型与数据混合驱动的决策方法
3.1 不均衡数据的模型定义与评价指标
3.2 元学习方法与集成模型
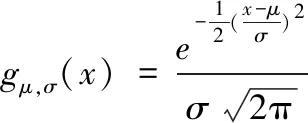

4 仿真研究
4.1 数据分析
4.2 基于元集成学习方法的训练
4.3 不均衡数据学习方法比较

5 结论与展望

