无人机系统地空信道建模与仿真
高 猛,屠 佳,纪雅峻,吴世凯
(1. 空军通信士官学校,辽宁 大连 116600;2. 国防科技大学国际关系学院,江苏 南京 210039)
1 引言
无人机(Unmanned Aerial Vehicles, UAVs)具有用途多样、灵活性强、装配便利和开支较低等优势,在军用、民用领域皆得到了广泛的关注和发展[1]。军用方面,无人机可应用于侦查、监视和火力打击等[2];民用方面,无人机在公众安全、运输管理以及有毒气体泄漏、深林火灾[3]、野生动物追踪等危险行动之中广泛使用。此外,无人机还可提供实时灾难预警、辅助救援行动,特别是在主干通信网络受损的情况下可作为中继节点以保证通信畅通[4]。其中,基于无人机辅助的高速移动环境下的无线通信更是未来移动通信发展的方向之一。无人机辅助无线通信可在山地、水面、城市和近郊地区等多种场景下建立短距离视距通信,实现主干通信补盲[5]、中继通信[6]、信息分发与收集[7],[8]等功能。
可以说,高效、实时、可靠的无线链路通信是无人机系统应用的基础保障。而在无人机广泛应用的背景下,为保证高速移动环境下无人机通信系统的QOS服务质量和其它应用需求,其面临着快时变信道建模与传输技术、高效移动管理策略、动态网络拓扑结构等诸多新的技术挑战亟待解决[9],[10]。其中,快时变信道建模与传输技术作为高速移动环境下无人机系统端到端通信的核心技术,既要保证频谱和能量效率,也要满足可靠和高速率信息传输需求。
正交频分复用(Orthogonal Frequency Division Multiplex, OFDM)技术以其高效地并行传输能力、天然的抗多径干扰性能和简单的信道均衡等优势,广泛应用于宽带数字无线通信业务之中。然而在高速移动场景下,无线信道呈现快时变特性,由多普勒频移所产生的载波频偏破坏了OFDM系统子载波间原有的正交性,从而引起严重的载波间干扰(Inter-Carrier Interference, ICI),导致系统性能大幅度下降[11],[12],[13]。研究表明,双散射信道下信号的时频网格结构将直接决定无线信道的多径时延和多普勒效应对系统性能的影响程度,OFDM等系统的矩形时频网格结构并不是最佳分布。而基于球填充理论的六边形多载波传输(Hexagonal Multi-Carrier Transmission, HMCT)系统可有效降低频谱泄露,在保证频谱效率和抗符号间干扰(Inter-Symbol Interference, ISI)性能的同时实现更优的抗ICI性能[14][16]。综上所述,高速移动环境下,HMCT系统可用于无人机宽带无线链路通信,提高其抗无线信道衰落损伤能力。
本文针对无人机通信系统的无线链路信道建模与调制等物理层关键技术进行研究,在分析无人机无线链路特性的基础上,归纳了无人机水面、山地与丘陵、城市与近郊等典型应用场景下的地空信道衰落特性,并构建了信道大尺度和小尺度衰落的数学模型,在此基础上,仿真分析OFDM和HMCT两种调制方式的无人机通信系统性能,从而期望为提升无人机系统通信链路性能提供理论依据和技术支撑。
2 UAVs无线通信链路特性
典型的无人机无线通信链路结构如图1所示[5]。由于无人机通信系统的特殊性,其端到端通信链路为非对称链路,上行链路仅为控制链路,信息速率较低,但其实时性、连续性和可靠性要求高,通常采用无线通信链路为主、卫星中继通信链路为辅的复合链路形式;而下行链路则包括控制链路和数据链路两部分。无人机通信数据链路为高传输速率的宽带无线链路,主要是用于支持地面终端的野外基站、移动终端、网关节点、无线网络传感器等各种应用。考虑无人机的高速移动特性导致无人机通信网无固定“回程”链路和中心控制节点,从而造成相邻用户干扰强。又由于无人机尺寸、载重和能量限制,即无人机端到端无线链路通信为功率约束下的强邻道干扰通信。

图1 无人机典型无线通信链路结构
从信道角度来说,无人机通信链路可分为空-空信道和地-空信道两类,其中空-空信道以直达路径分量为主导,多径分量影响相对较小,然而其收多普勒衰落影响严重。以最大移动速度为500km/h的无人机为例,无人机之间的高速相对移动性,将产生极大的多普勒扩展,若系统中心频率为5GHz(C波段),则最大多普勒频移为fD=2314Hz(信道相干时间≈216μs),远高于目前无线通信系统的设计标准。
无人机通信系统地-空信道由于其应用环境的复杂多变,特别是中低高度飞行的情况下,由于山体、水面、树林、建筑物等影响而产生的无线电波反射、散射和绕射,其信道特性更为复杂。总体来说,无人机通信系统地-空信道具有如下基本特征:1)多数情况下存在直达路径;2)障碍物或机体自身阴影衰落严重;3)多径衰落和多普勒衰落同时存在,且多径分量具有显著的稀疏特性,即信道传输能量集中在少数几条路径上;4)受地形地貌的影响较大,不同应用场景下信道多径衰落特性明显不同。
3 地空信道建模
无人机通信中无线信道衰减的影响不容忽视,因此地空信道建模对于系统参数设计及性能优化则尤为关键[17]。现阶段无人机实际可用规划频带范围为L波段17MHZ(960-977MHz)、C波段61MHZ(5.03-5.091GHz),其中,L波段频谱占用率较高,C波段更适合无人机大容量可靠通信[18]。下面将以C波段为例,按照水面、山地与丘陵、城市与近郊等不同应用场景构建无人机地空信道模型。
3.1 水面环境
水面应用场景下,较早的地空信道建模研究成果为文献[19],文中提出了基于几何结构的平坦衰落信道模型,其将直达路径和多径成分建模为复高斯正交分量。文献[20]针对配备高增益、窄波束基站天线的航空遥感系统,提出了2GHz频段的窄带信道模型;文献[21]以小型无人机为研究对象,在极低飞行高度情况下,提出了900MHz频段的时延扩展、多输入多输出(multiple-input-multiple-output, MIMO)信道参数。文献[22]将水面环境下无人机系统地空信道建模为两径信道模型与随机第三径分量的混合模型,并采用地球曲率两径(Curved-Earth Two-Ray, CE2R)模型建模地空信道的直达路径和反射路径的衰落模型。
如图2所示,无人机系统发射信号经地空信道传输时受到大尺度路径衰落、阴影衰落和小尺度衰落的共同影响[24],[25]。水面场景下,无人机系统接收信号功率可按下式计算

图2 窄带地空信道模型[23]
Pr=Pt+GHPA+GLNA+Gt+Gr-LC-PL(R)-LS
(1)
式中,Pt为发射功率,GHPA为C波段高频功率放大器增益,GLNA低噪声放大器增益,Gt、Gr分别为发射天线和接收天线增益,LC是有线(光纤)路径损耗,C波段为7.5dB。
3.1.1 路径损耗
PL(R)是与距离R相关的信道模型路径损耗,采用CE2R信道模型时,其路径损耗可表示为[22]
Rmin≤R≤Rmax
(2)
上式为对数距离模型,其中R表示链路范围(千米),Rmin为最小有效链路距离(千米),A0为最小链路距离对应路径损耗,n为路径损耗系数,运动方向系数ζ=-1表示“向”基站方向运动,ζ=1表示远离基站方向运动,Γ为运动方向微调系数(因多数情况下无人机机头处于“仰”的状态,Γ>0),X为零均值、标准方差为σx的高斯随机变量。
3.1.2 阴影衰落
阴影衰落LS在中短路程地空链路情况下,与地形阴影以及建筑物、树木阴影相比,机体阴影衰落的影响更大,这里将主要针对机体阴影衰落进行研究。机体阴影衰落特性与机型、飞行姿态密切相关,而与航线、飞行距离等无关,可将其建模为时间的函数LS(t),可表示为
LS(t)=Sf(t)
(3)
式中,S为平均阴影衰落深度随机变量,可表示为飞机横滚角Roll(单位度)的函数,如下所示
S(Roll)=AS,Roll+nS,Roll(Roll-Rollmin)+XS,Roll
(4)
式中,AS,Roll表示最小横滚角Rollmin对应的阴影衰落(dB),表示拟合函数斜距(dB/°),nS,Roll表示斜率,XS,Roll为零均值、标准方差σX,S,Roll的高斯随机变量。
f(t)为基于最小二乘准则的三阶多项拟合函数(三次样条插值),表示阴影衰落持续时间D的概率(百分比),可表示为
f(t)=ai(t-ti)3+bi(t-ti)2+ci(t-ti)+di
(5)
式中,多项式系数ai、bi、ci和di可由(ti,f(ti))∈(0,0),(0.5,1),(1,0)三个关键点决定。
经处理,式(3)可变换为链路距离R的函数,以保证式(1)中各分量的参数一致性,其变换关系为
R=υHtcos(∠HA)cosθ+υVtsinθ
(6)
式中,υV和υH为水平和垂直飞行速度,θ为俯仰角,∠HA表示机头方向和方位角间的偏差角。
当垂直速度或俯仰角大时,链路距离R和时间t之间是三维关系,如起降阶段,除此之外,俯仰角小,上式可近似表示为
R≅υtcos(∠HA)
(7)
式中,υ为合成后速度或水平速度,且近似认为速度和角度变化慢。
3.1.3 小尺度衰落
水面环境下,无人机系统宽带地空信道呈现稀疏特性,一般可建模为两径信道模型与随机第三条多径分量的混合模型。如图3所示,其信道冲激响应(channel impulse response, CIR)可表示为

图3 抽头延时线信道模型
hOW(τ,t)=h2-ray,F(τ,t)+z3(t)a3(t)e-jφ3(t)δ(τ-τ3(t))
(8)
式中,h2-ray,F(τ,t)表示CE2R信道模型,随机变量z3(t)表示有无第三条多径分量,z3∈{0,1},第三径分量出现概率可采用指数函数拟合,表示为p(R)=aebR,其中,a=0.03,b=-0.15,距离R的单位为千米;α3、φ3和τ3分别是第三条路径幅度、相位和时延。其中,第三径分量的最大时延扩展范围为0.1μs≤τ3≤1.1μs,且服从负指数分布,与出现概率分布相同;相位φ3在[0,2π)之间呈均匀分布;幅度α3可视为高斯变量,其均值、方差分别低于直达分量幅度μ3dB、σ3dB,海面时,μ3=22.6、σ3=5.2,湖面时,μ3=23.2、σ3=3.9。并且,CE2R信道模型h2-ray,F(τ,t)可表示为
h2-ray,F(τ,t)=δ(τ-τ0,k)+αs,n,ke-jπΔRk/λΓk,FDkrFδ(τ-τs,k
(9)
式中,k为时间序号,F表示频带宽度,ΔR=R2,k-R1,k,R1,k为直达路径距离,R2,k为反射路径距离,τ0,k=R1,k/c,τs,k=Rs,k/c,αs,n,k=R1,k/R2,k,Γk,F为表面反射系数,取决于频率、极化方式、入射余角和介电常数,rF表面起伏因子,Dk为散射因子。表面起伏因子r通常假设为Gaussian分布(相对高度),与波长、入射波余角有关,水面环境下也与风速有关。
水面环境下,地空信道绝大多数情况都存在直达路径,且Rician因子K与距离R(km)可表示为K(R)=K0+nK(R-Rmin)+Y。其中,K0为最小距离Rmin对应莱斯因子(C波段为2.2km),nK为斜率,Y是均值为0、方差为σY的高斯随机变量。一般情况下,斜率nK较小,因此上式可近似为K(R)≌K0+Y,海面K0=29.9dB,σY=1.7dB,湖面K0=11.7dB,σY=1.1dB。
此外,对于两径模型来说,其最大多径时延(maximum excess delay)τ2,max=2hG/c,c为光速,hG为基站天线高度,大多数情况下天线高度hG<30m,对应τ2,max≤200ns,仅当无人机在基站正上空时时延扩展达到最大值200ns,其它位置时延扩展较小。并且,信道的变化率取决于信道平稳距离(无人机飞行速度×信道平稳时间),对于视距信道来说,C波段信道平稳距离约为250λ(15m),大于非视距信道的20λ~40λ。
3.2 山地与丘陵环境
文献[26]和[27]分别分析了山地与丘陵环境下的无人机系统地空信道特征;文献[28]考虑链路范围、方位角、飞行速度、飞行高度、地面站高度、地面海拔、表面起伏因子等因素具体给出了山地与丘陵场景的无人机系统地空信道模型及详细参数设置。
山地与丘陵环境下,无人机系统地空信道水面环境的区别主要体现在“表面”特性的不同,即由于地面起伏、植物覆盖以及建筑物所导致的表面粗糙系数、反射系数等信道参数的差异。山地与丘陵环境下,地空信道路径损耗可采用式(2)所示的路径损耗模型建模,其信道冲激响应(CIR)可表示为
h(τ,t)=αLOS(t)δ(τ-τ1(t))+α2(t)e-jφ2(t)δ(τ-τ2(t))

(10)

上式中前两项为CE2R模型,与式(8)所示的水面场景相比,山地与丘陵场景应增加表面粗糙系数Cr,可表示为
Cr=4πsgsin(ψ)/λ
(11)
其中,ψ为入射波余角,λ表示波长,sg为地面起伏高度的标准方差,且sg的准确估计需要地面站和飞行路线的详细地理位置信息,且在Q点附近区域(如图4所示),一般情况下可假设sg>10m。当Cr>10时地面反射影响可忽略,Cr<0.1时地面较光滑,反射效果强。对应地,式(9)中的表面起伏因子rF可表示为

图4 地面反射点
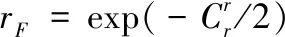
(12)
“偶现”路径分量的相对功率决定于散射体或反射体特征,且参数zk、τk和多径分量持续时间Dk可表示为时间或距离函数形式,其与基站附近环境有关,且随链路距离增大而呈指数形式变化,可采用线性模型拟合,如下所示
Log10(y)=C0+nyR+Z
(13)
式中,y表示第k径路径分量且其时延为τk、持续时间为Dk,C0为最小范围Rmin对应数值,ny为斜率,Z为零均值、标准方差σZ的高斯随机变量。
此外,由于多径分量持续时间较短,一般≤20ms或更短,因此对于这些路径分量来说,短期多普勒频移特征难以估计,且多径分量的功率较小也给多普勒特征估计带来更大困难。
3.3 城市与近郊环境

4 六边形多载波系统
现阶段,HMCT系统的研究可分为两大类[31]:一是基于正交原型脉冲成形的HMCT系统,即网格正交频分复用(Lattice OFDM, LOFDM)系统,其由高斯函数的正交化函数集构成原型脉冲成形函数[32][33];二是基于非正交原型脉冲成形的HMCT系统,即HMT(Hexagonal Multicarrier Transmission)系统,其利用非正交高斯脉冲成形函数实现高鲁棒性的抗信道时频散射的性能[34]。具体而言,对于HMCT关键技术的研究主要集中于以下五个方面:信号优化与设计[32]-[34],系统定时与载波同步[35][36],峰均比抑制[38],最佳接收与检测[39],[40],信道估计[41]-[43]。
与OFDM系统的矩形时频网格不同,HMCT系统采用时频交错的六边形网格结构,如图5所示,其中T和F为网格时间、频率间距。HMCT调制采用无CP保护的信号结构,其发送信号可表示为

图5 HMCT系统时频分布表示

(14)

经双散射信道传输后,HMCT系统接收信号为式中,w(t)表示加性高斯白噪声,h(τ,t)为时频散射信道H复冲激响应。
5 地空信道链路性能仿真
本节将以OFDM和HMCT调制为例,仿真分析水面、山地与丘陵、城市与近郊三种环境下的无人机地空无线信道的大尺度衰落路径损耗、机体阴影衰落及小尺度衰落等链路特性对系统性能的影响。

(15)

以中型无人机为对象,飞行速度为100m/s,飞行高度为800m,机载天线为增益5dB的方位全向天线,地面站天线为定向天线,方位波束扫描范围180°,俯仰波束宽度35°,距地面高度20m,天线增益6dB,发射机功率10W,发射机高放增益7dB,接收机低放增益30dB,接收机光纤损耗7.5dB。此外,设置接收机噪声平均电平值为-80dBm,并且考虑突发干扰以及强接收机噪声对系统性能的影响,设置16dB的噪声余量。
无人机系统地空信道的大尺度衰落路径损耗、机体阴影衰落和小尺度衰落模型依据第三章相关数学模型进行仿真建模,信道主要特性参数如表1所示。

表1 地空信道主要特性参数
图6、图7和图8在理想同步和理想信道均衡的条件下,仿真比较了水面、山地与丘陵、城市与郊区三种场景下的HMCT和OFDM调制的系统误符号率性能。由图可知,三种场景下的HMCT和OFDM调制都表现出较好的误符号率性能,且随着链路距离的减小,系统性能有着明显改善,究其原因是接收机噪声电平一定的情况下,接收信噪比的大小主要取决于路径损耗,从而体现出路径损耗在一定情况下对于系统误符号率性能的决定性影响。然而,当链路距离较小时(≤10千米),HMCT调制的误符号性能改善要明显优于OFDM调制,且链路距离越小HMCT调制的优势越大,其原因在于此时噪声对于系统性能的影响减弱,而ISI/ICI干扰对系统性能的影响更大。由第四章的分析可知,OFDM调制受ICI干扰影响较大,HMCT调制可在不额外增加系统开销的情况下,同时实现良好的抗ISI/ICI性能,本章的仿真分析也验证了这一点。同时,OFDM调制是利用循环前缀(Cyclic Prefix, CP)来克服由于信道多径衰落所导致的ISI干扰的影响,而仿真中为了保证两种调制方式的系统频带利用率相同,设置CP长度为固定值,不能保证在三种环境下都满足CP长度大于信道最大多径数,这也会进一步降低OFDM系统性能。
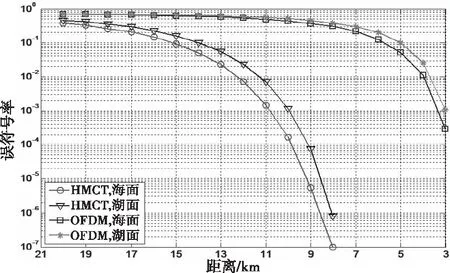
图6 水面环境下,HMCT和OFDM调制系统误符号率性能比较

图7 山地与丘陵环境下,HMCT和OFDM调制系统误符号率性能

图8 城市与近郊环境下,HMCT和OFDM调制系统误符号率性能
6 结束语
无人机系统需要不间断地传输上行控制指令数据,又需要满足遥测数据及音视频采集数据的高速率回传通信需求,然而其无线通信环境复杂多变,且受衰落影响严重。无人机通信链路可分为空-空信道和地-空信道两类,其中空-空信道以直达路径分量为主导,多径分量影响相对较小,然而其受多普勒衰落影响严重。而地-空信道特性更为复杂,路径损耗、机体阴影衰落、时频散射衰落等同时存在,且受地形地貌的影响较大,不同应用场景下信道多径衰落特性明显不同。OFDM和HMCT两种多载波调制技术皆可作为无人机数据链系统的物理层关键技术,从技术成熟度和实现复杂度方面来说OFDM技术更具优势,而HMCT调制具有更优的抗无线信道衰落损伤能力,但其需要准确地估计并匹配信道状态信息,相应地系统实现复杂度较高。

