微型堆SCO2布雷顿循环系统构型及参数优化

梁铁波,唐 鑫,钱奕然,赵全斌,陈伟雄,*,严俊杰

(1.中国核动力研究设计院,四川 成都 610213;2.西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049)

微型反应堆一般功率在15 MW以下,采用模块化设计,可以灵活机动部署、远离电网独立运行,能满足偏远地区、孤立海岛和沙漠地区等多种场景下的能源需求。超临界二氧化碳(SCO2)布雷顿循环由于其具有高循环效率、高容量/功率比、结构紧凑等优点而在核电领域有很好的前景,很适合作为微型反应堆的能量转换系统,国内外学者也对其开展了广泛研究。

2004年Dostal等[1-2]建立了再压缩SCO2循环模型及参数优化方法,与其他动力循环对比表明,SCO2循环系统具有高效、简单、紧凑、经济等优势,非常适合第四代反应堆。Dostal后续研究表明,与简单回热循环相比,单级压缩机级间冷却和透平再热可使循环效率分别提升3.75%和2%,并指出再压缩循环是最适合下一代核电系统的循环构型之一[3]。Ahn等[4]比较了12种SCO2循环构型,也得出了SCO2再压缩循环性能最好,最适合下一代核电系统的结论。Sarkar等[5]对带有一次再热的SCO2再压缩循环进行了优化,指出与无再热构型相比,再热可以使循环热效率提高3.5%。美国德克萨斯大学圣安东尼奥分校的Patel等[6]正在建设一个小型闭式SCO2循环实验系统,前期理论分析表明,对于采用往复活塞式压缩机和膨胀机的无回热简单循环系统,在膨胀机入口压力和温度分别为17.23 MPa和358.15 K时,系统可产生4.5 kW的电功率,系统热效率估计为12.75%。Xin等[7]为评价不同构型的SCO2循环的性能,提出了热循环分裂分析方法,将复杂的SCO2循环分为简单的主循环和简单的等效功率循环,并采用这种新分析方法对SCO2再压缩、中冷和再热3种循环进行了对比,并提出了一种新的部分中间冷却循环构型,最终循环效率可达到53.58%。黄潇立等[8]基于热力学第一定律,研究了系统采用再压缩循环和复叠式分流循环方案的热力学特性和参数限制条件,并讨论了两种循环各自的适用场景。段承杰等[9]对再压缩SCO2循环参数进行优化,结果表明再压缩循环适宜作为出口温度较低的反应堆能量转换系统。

关于耦合微型反应堆的SCO2布雷顿循环研究,美国MegaPower微型堆采用热管堆固态堆芯,能量转换系统采用SCO2循环,输出电功率在2.25～17.5 MW之间,能达到40%的发电效率[10];美国洛斯阿拉莫斯国家实验室(LANL)设计的微型热管堆也采用SCO2循环进行能量转换,包括运输容器在内时,其质量约35～45 t,尺寸为φ1.8 m×3.6 m,可以通过卡车或航空运输轻松部署[11];韩国研发的可移动式微型堆功率等级在10～20 MW,主要方案采用高温气冷反应堆耦合SCO2循环以及氦气循环,反应堆总质量约40 t,透平入口温度650 ℃,冷端采用空气冷却,研究对比了SCO2循环以及氦气循环系统循环结构和运行条件,并对系统各部件进行了初步选型设计,研究发现,SCO2循环性能一般高于氦气,氦循环的体积与叶轮机械效率高度相关,而SCO2循环的体积与叶轮机械效率相关度较小,采用级间冷却能提高效率且不会使换热器体积显著增加[12-13]。中国工程物理研究院提出了热管型反应堆耦合SCO2布雷顿循环核动力装置,并给出了3.5 MW海洋热管堆总体设计方案,采用SCO2简单回热和分流再压缩方案,循环热效率均达到30%以上[14]。Yun等[15]对用于氟化物-钠冷却的高温反应堆SCO2布雷顿循环进行了构型以及温度、压力等参数的设计优化,采用粒子群优化算法求解简单回热循环的最优热效率,并提出了4种改进构型,结果表明再热中冷循环的热效率最高可以达到51.64%。Du等[16]建立了核动力船舶SCO2再压缩循环的热力学模型,利用深度学习和数据挖掘技术对该循环进行优化,并考虑了系统热效率和总部件体积的协调优化,结果表明,基准优化下的最优热效率和总部件体积分别为39.92%和3.92 m3,该研究结果对高维度设计空间的SCO2再压缩循环在空间和能量受限场景下的优化设计具有指导意义。

现有对于SCO2布雷顿循环的研究大多基于特定场景和应用领域,且大多研究基于热力学优化,不能很好兼顾系统高效性和紧凑型,缺乏高效匹配微型堆的SCO2布雷顿循环系统构型及参数优化研究以及系统关键部件选型设计。因此,本文拟对SCO2布雷顿循环系统关键部件进行选型及热力设计,并通过建立设备模型及系统整体分析模型,进行不同构型参数优化,获得不同优化目标下最佳构型及最优参数配置,为获得匹配可移动微型堆的高效、安全、灵活的能量转换系统提供参考。

1 SCO2布雷顿循环系统建模及验证

1.1 研究对象

本研究选取简单回热循环(SRC)、再热回热循环(RRC)、再压缩循环(RC)、再压缩再热循环(RHRC)共4种构型的SCO2布雷顿循环系统(图1)作为研究对象。其他构型是在简单回热循环基础上进行构型改进,采用再热器来对工质再热,通过提高吸热平均温度来提高效率,而采用工质再压缩能解决换热器“夹点”问题,通过这些构型改进以实现SCO2布雷顿循环性能的提升。

a——SRC;b——RRC;c——RC;d——RHRC

1.2 系统各部件模型

表1 系统各部件热力学模型

1.3 系统分析模型

微型堆SCO2布雷顿循环系统不仅要求系统具有高效性,同时也要求系统体积和质量较小,有很好的紧凑性,从而能更好地实现在可移动场景下的应用。因此,本文采用发电效率、火用效率、功率密度和功率质量比作为系统性能评价指标,以此兼顾系统高效性与紧凑性。

系统发电效率表达式如下:

(1)

系统火用效率表达式如下:

(2)

常规热力学建模及分析优化是以效率作为优化评价指标,这能提高系统的高效性却不能很好地兼顾系统的紧凑性。因此,本研究提出采用功率密度(Dp)和功率质量比(Mp)也作为系统分析及优化设计的评价指标,以较好地兼顾系统的高效性和紧凑性。功率密度定义为系统单位体积的净输出功率(W/m3);功率质量比定义为系统单位质量的净输出功率(kW/t)。其计算公式如式(3)、(4)所示。在计算过程中主要考虑反应堆及各换热器的体积及质量,而压缩机和透平由于其尺寸较换热器小得多(小于1%),故在计算中忽略以作简化。

(3)

(4)

1.4 模型求解

本研究具体模型求解流程如图2所示。首先在Ebsilon软件中建立系统热力学模型,并在Matlab软件中编写好部件热力学设计子程序,利用Ebsilon软件的编程接口与Matlab进行连接;求解前在模型中预设循环边界参数,包括压缩机等熵效率ηc、透平等熵效率ηt和换热器压力损失Δp;在求解过程中先通过Ebsilon软件计算得到循环各点热力学参数,以此作为Matlab部件设计程序的边界值进行热力学设计;将部件热力学设计结果带入Ebsilon模型进行修正并进行迭代计算直至收敛;最后输出热力学参数和循环设计结果,包括发电效率ηe、火用效率ηex、功率密度Dp和功率质量比Mp。

图2 模型求解流程图

1.5 模型验证

热力学模型是建模分析的基础,为确保所搭建模型的准确性,需要对SCO2布雷顿循环模型进行验证。本研究与马岳庚[17]及Wang等[18]所研究的再热再压缩SCO2循环模型进行对比验证。模型验证的初始条件如表2所列,相同循环参数下,本文模型与文献所用模型计算的循环热效率如图3所示。计算可得,在设计参数下,不同透平入口温度条件下,循环热效率的本文模型计算值与文献值的最大相对误差为1.64%,从而证明了本文SCO2布雷顿循环模型计算的准确性。

表2 模型验证初始条件

图3 模型验证结果

2 系统关键部件选型设计

进行系统的优化设计研究不仅要进行构型及热力学参数优化,也要考虑系统部件及整体的选型设计,这对推动SCO2布雷顿循环系统实际应用具有重要意义。本研究主要针对系统反应堆、各换热器、透平和压缩机部件进行选型及热力学设计。

2.1 反应堆选型

通过文献调研发现,微小型反应堆大多采用气冷堆或热管堆,通过消除中间回路以提高系统紧凑程度,在1～10 MW功率等级多采用热管堆,其具有高可靠性和很好的热瞬态反馈性能[11]。本研究采用美国爱德华实验室(INL)[19]公布的5 MW热管堆设计方案,其结构如图4所示,它是由一个六边形不锈钢(SS-316)组成的整体结构,热管采用液态金属钾(K)热管,工作温度为675 ℃,其主要参数如表3所列。

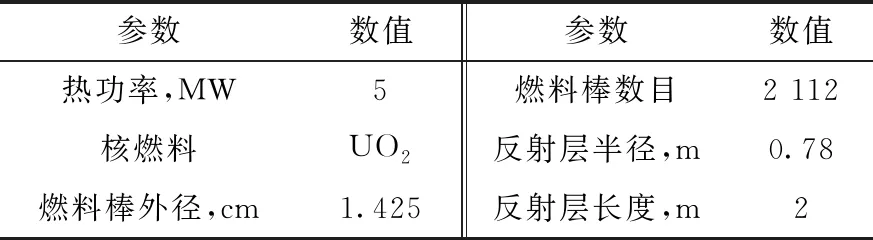
表3 热管堆主要参数[19]

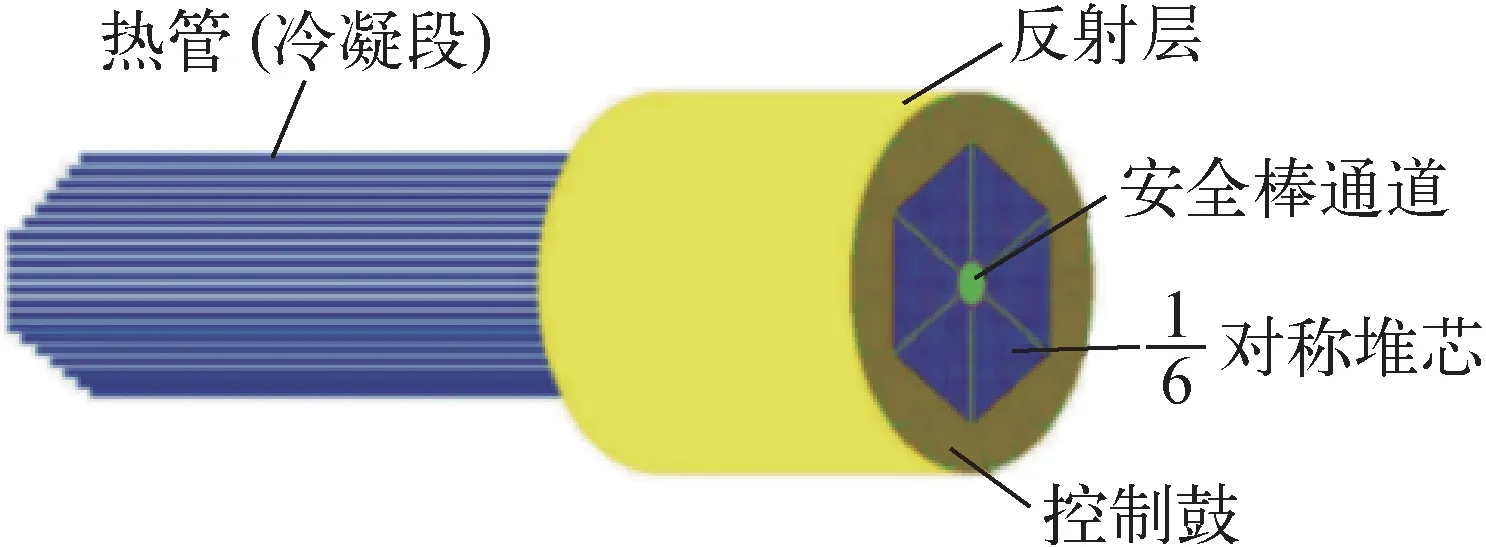
图4 热管堆结构示意图[19]

根据文献[19]中的热管堆结构及数据,本研究采用式(5)、(6)估算热管堆的体积(Vrea)和质量(Mrea):

(5)

Mrea=Mfuel+Mmatrix+Mreflector+MHP,evaporator

(6)

其中,下标fuel、matrix、reflector和HP,evaporator分别代表堆芯燃料、刚体、反射层和热管热端。

2.2 各换热器选型设计

换热器设计流程图如图5所示。当选定某个换热器类型时,通过给定两侧工质及进出口热力边界,采用换热器设计程序进行设计计算,得到换热器设计参数,并通过校核确保换热面积和压力损失满足要求。

图5 换热器设计流程图

主换热器及再热器位于热管的冷凝段,采用管壳式布置,即工质与热管横向冲刷以获得更好换热效果,同时增加了折流板来强化换热,其结构如图6所示。热管冷凝段体积(VHP)以及质量(MHP)计算公式如下:

图6 主换热器及再热器结构示意图

(7)

MHP=Mshell+Mbaffle+MHP,condenser

(8)

式中:DHP为壳体圆筒直径;LHP为换热管冷凝段长度;下标shell、baffle和HP,condenser分别表示翅片、折流板和热管冷端。

回热器利用透平出口乏气热量加热压缩机出口工质,运行压力及温度较高,因此本研究回热器采用有较高承压及耐高温能力的印刷电路板换热器(PCHE),如图7所示,回热器内部设计为半圆形直通道、单层冷热流道交替排布的结构,材质为304不锈钢。回热器的体积(VRG)以及质量(MRG)计算公式如下:

VRG=WHLRG

(9)

MRG=(VRG-NAcLRG)ρRG

(10)

式中:W为迎流面宽度;H为迎流面高度;LRG为流道长度;N为流道数;Ac为流道截面积。

微型堆可移动部署,系统可能常处于缺水状态运行,因此冷却器采用空冷设计更符合实际情况。本文空冷冷却器采用扁平翅片管式换热器,如图8所示,高压的热工质在管内流动以满足承压要求,冷空气在管外横向冲刷换热,并通过增加整体翅片来强化传热,采用扁管有利于减小冷空气侧阻力。冷却器的体积(VC)及质量(MC)计算公式如下:

VC=ABLC

(11)

MC=Mshell+Mfin+Mtube

(12)

式中:A为冷侧迎风面宽度;B为冷侧流动长度;LC为换热管长度;下标shell、fin和tube分别代表冷却器外壳、翅片和换热管。

系统中各换热器的主要结构设计参数及设计压降列于表4。

表4 各换热器设计参数

2.3 压缩机及透平选型设计

透平和压缩机的选型需要与系统功率等级相匹配,文献[20]给出了不同系统功率等级SCO2布雷顿循环的透平和压缩机选型范围,功率小于10 MW时,透平和压缩机建议采用单级径流式结构。因此,本文采用单级离心式压缩机和向心式透平设计,如图9所示。通过给定压缩机、透平边界参数,采用程序进行一维热力学设计,得到叶轮机械详细结构参数和性能参数等。

图9 叶轮机械结构示意图

3 不同构型系统参数优化

3.1 循环构型及参数优化模型

SCO2布雷顿循环关键参数对循环性能影响明显,主要包括压力、温度及分流比等参数,其会对效率、功率密度及功率质量比指标产生较大影响。参数优化的冷热端边界设计参数如表5所列。本研究以不同评价指标作为优化目标在Matlab中采用遗传算法工具箱进行不同构型系统的多参数优化,以获得不同优化目标下的最佳构型及最优参数配置。不同构型的主要优化变量选择及优化范围如表6所列。

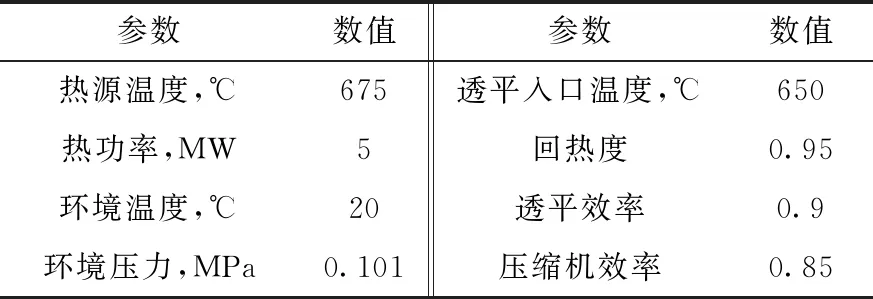
表5 循环边界设计参数

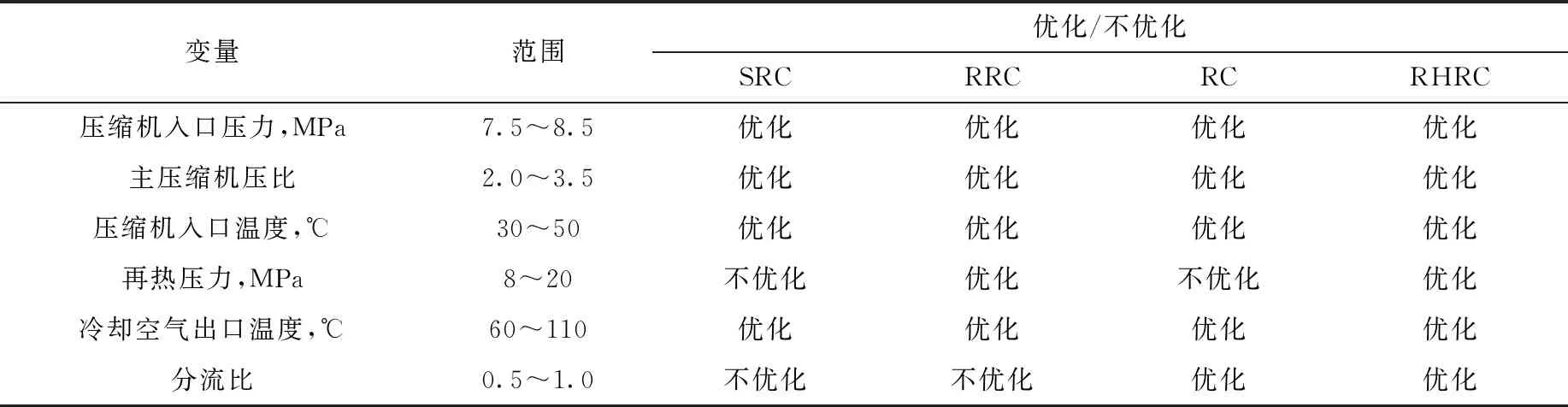
表6 优化变量及范围

3.2 以发电效率最大为目标优化

本研究首先以发电效率最大作为优化目标,对4个循环构型进行多参数优化,以期获得最高效的循环构型及参数。各构型参数优化后的最佳值及对应的系统性能评价指标如表7所列。

表7 以发电效率最大为目标的优化结果

不同构型在以发电效率最大作为优化目标优化后的评价指标如图10所示。由图10可见,以发电效率最大作为目标优化后,SCO2循环各构型发电效率均可达到40%以上,其中最优的是RHRC构型,其发电效率可达到47.5%,但该构型功率密度和功率质量比与其他构型相比没有优势,此时RC构型功率密度最大可达255.1 kW/m3,SRC构型功率质量比最大可达96.1 kW/t。

图10 以发电效率最大为目标优化后各构型的评价指标

以发电效率最大为目标优化后,各构型的体积及质量如图11所示。由图11可见:各构型中,RC构型的系统体积最小,为9.3 m3;SRC构型的系统质量最小,为21.66 t;反应堆体积及质量在系统中占比较大;对于SRC和RRC构型,冷却器体积及质量在换热器中占比最大,而对于采用了再压缩的RC和RHRC构型,冷却器体积在换热器中占比最大,回热器质量在换热器中占比最大,这是由于再压缩时需要同时使用高温和低温回热器。

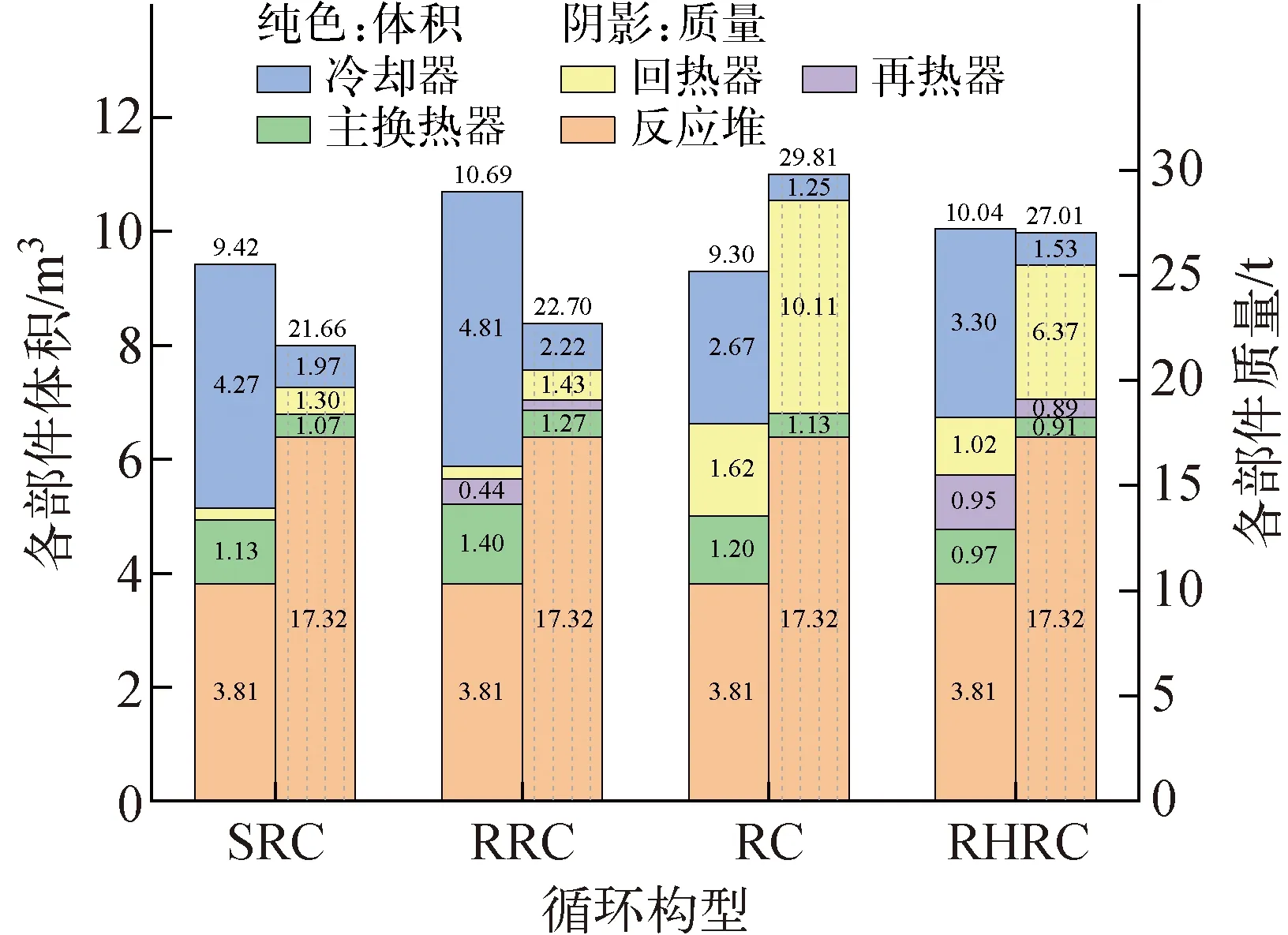
图11 以发电效率最大为目标优化后各构型的体积及质量

以发电效率最大为目标优化后,各构型的部件火用损如图12所示。由图12可见,SCO2循环构型中RHRC构型的火用损最小,RC与RHRC接近,而未采用再压缩的SRC和RRC构型总火用损较大,表明再压缩布置能减小SCO2循环火用损;对于各部件,SRC和RRC构型中回热器火用损占比最大,而采用了再压缩的RC和RHRC中,冷却器的火用损占比最大。

图12 以发电效率最大为目标优化后各构型部件的火用损

3.3 以功率密度最大为目标优化

为了更好兼顾系统高效性和紧凑性,不仅要考虑效率也要考虑系统体积,故本研究又以功率密度最大作为优化目标,对4个循环构型进行了多参数优化,各构型参数优化后的最佳值及对应的系统性能评价指标如表8所列。

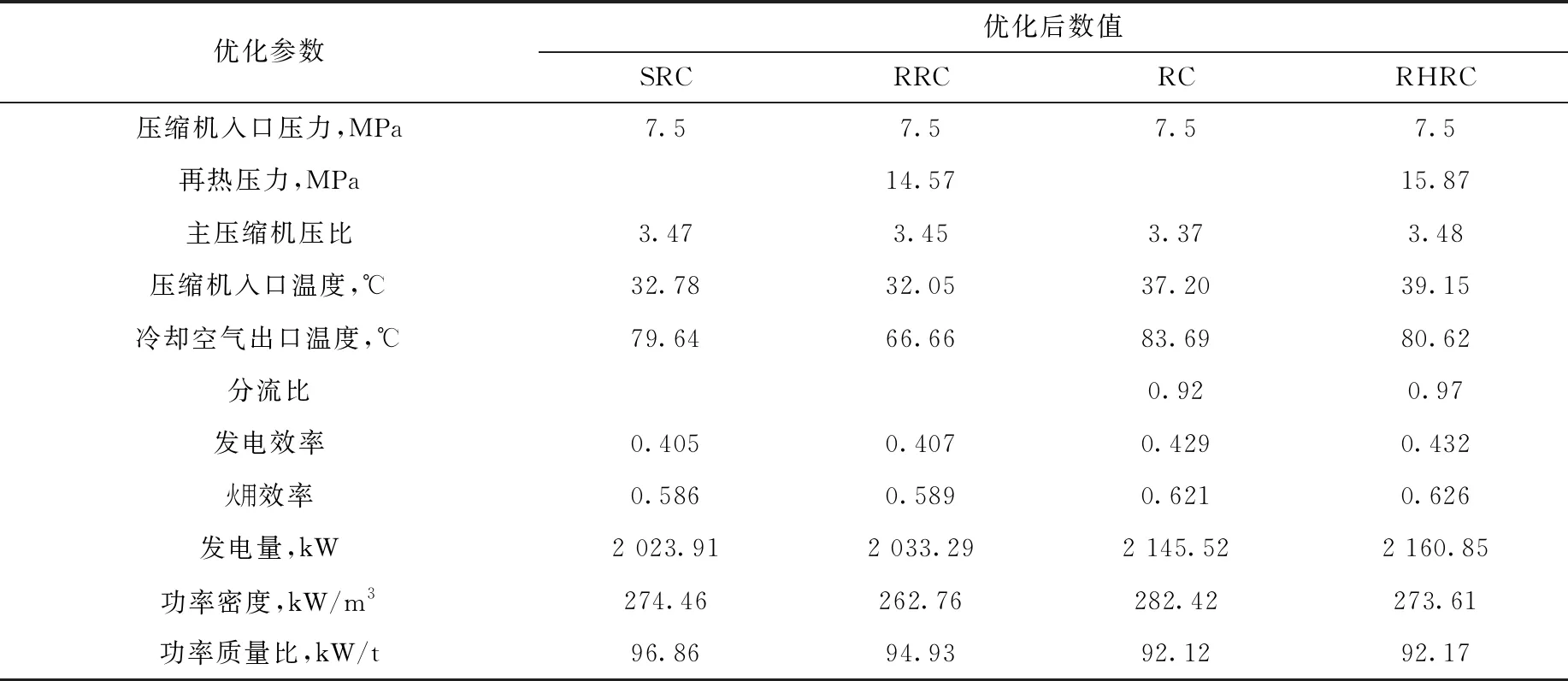
表8 以功率密度最大为目标的优化结果

以功率密度最大作为目标优化后,各构型的评价指标如图13所示。由图13可见:以功率密度最大作为优化目标下,最优的是RC构型,其功率密度最大可达282.42 kW/m3,而RHRC发电效率较高,可达43.2%,SRC功率质量比最大,可达96.86 kW/t;各构型的发电效率均小于以发电效率最大作为目标优化时的,这是由于以功率密度最大为目标优化时,牺牲了部分高效性来提高紧凑性。

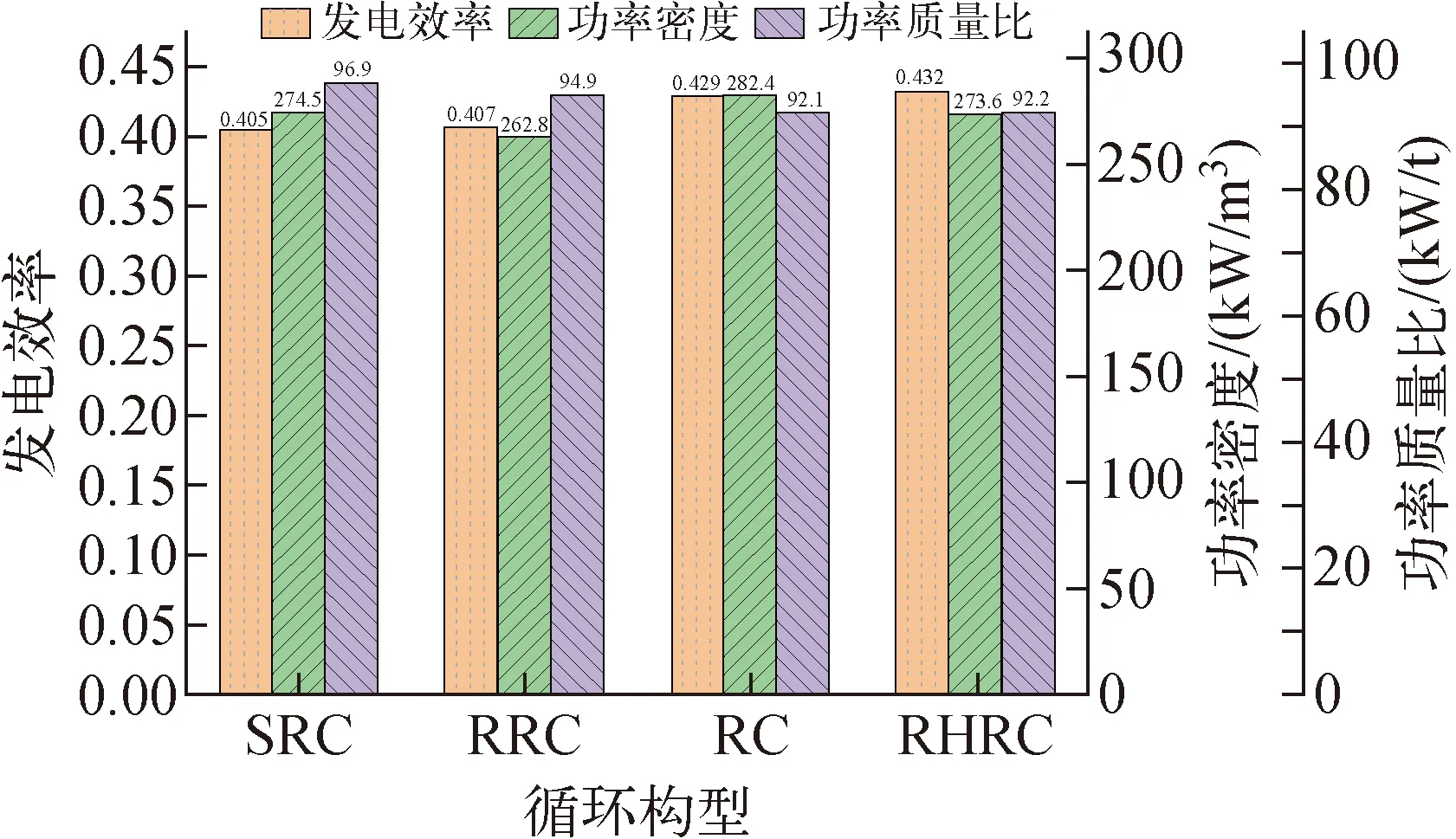
图13 以功率密度最大为目标优化后各构型的评价指标

以功率密度最大为目标优化后,各构型的体积及质量如图14所示。由图14可见:以功率密度最大为目标进行优化时,各构型的总体积差距较小,在1 m3以内,而质量差距在3 t以内;SRC构型的系统体积和质量最小,冷却器在换热器体积中占比最大,回热器在换热器质量中占比最大。

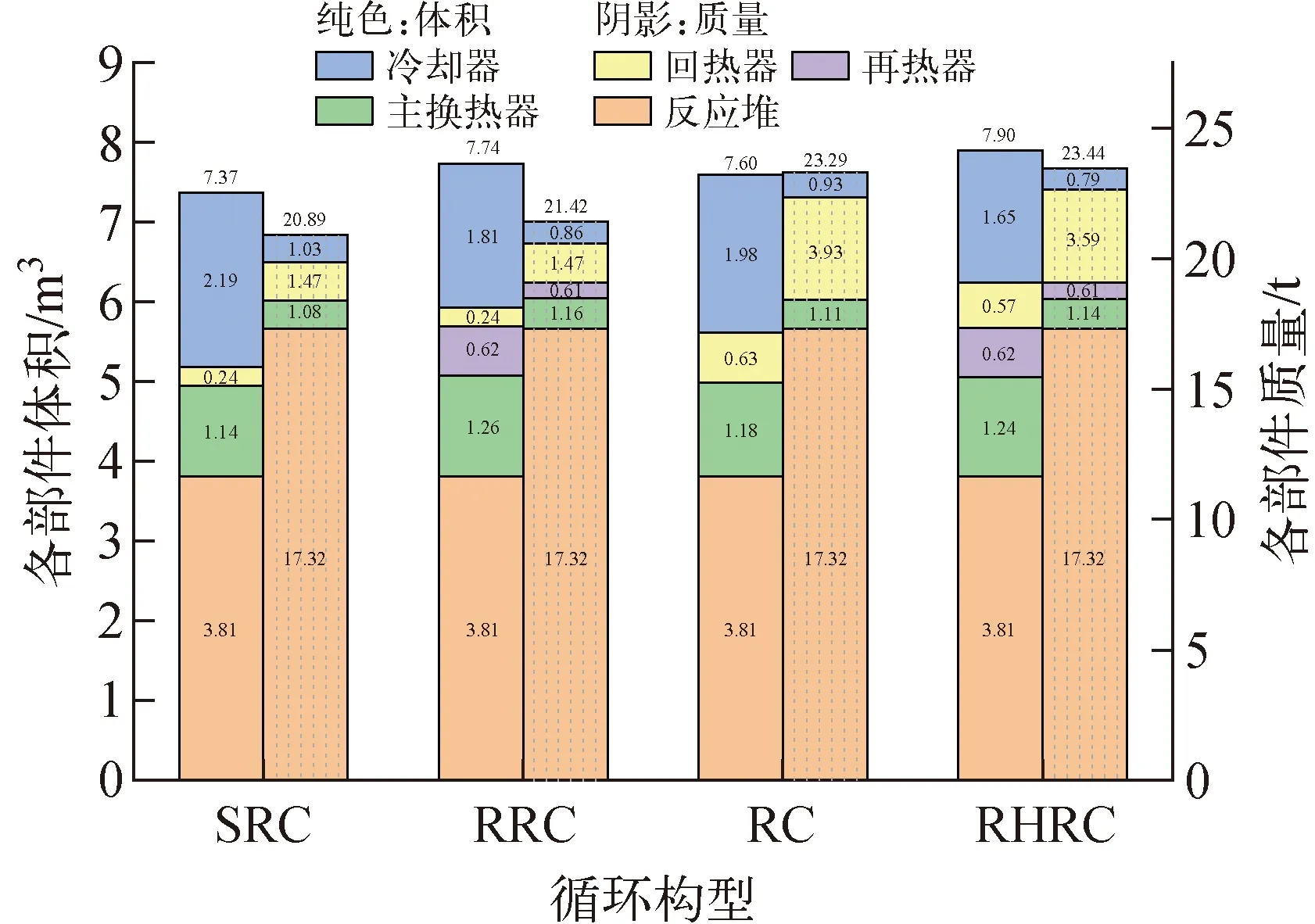
图14 以功率密度最大为目标优化后各各构型的体积及质量

以功率密度最大为目标优化后,各构型的部件火用损如图15所示。由图15可见,以功率密度最大为优化目标下,RHRC构型的火用损最小,在SRC和RRC构型中回热器火用损占比最大,而再采用了再压缩的RC和RHRC中,冷却器的火用损占比最大,表明再压缩会减小回热器火用损且增大冷却器火用损,而采用再热的构型回热器火用损更大。以功率密度最大为优化目标下,各构型的总火用损均大于以发电效率最大为优化目标下各构型的总火用损。

图15 以功率密度最大为目标优化后各部件的火用损

3.4 以功率质量比最大为目标优化

为了更好兼顾系统高效性和紧凑性,不仅要考虑效率也要考虑系统质量,故本研究又以功率质量比最大作为优化目标,对3个循环构型进行多参数优化,优化后各构型的参数及对应的系统性能评价指标如表9所列。

表9 以功率质量比最大为目标的优化结果

以功率质量比最大为目标优化后,各构型的评价指标如图16所示。由图16可见,以功率质量比最大为优化目标下,最优的是RC构型,其功率质量比最大可达到98.81 kW/t,而RHRC发电效率较高,可达45.2%,RC功率密度最大可达279.36 kW/m3。

图16 以功率质量比最大为目标优化后各构型的评价指标

以功率质量比最大为目标优化后,各构型的体积及质量如图17所示。对比图17与图14可知,以功率质量比最大为目标优化后,各构型的体积及质量规律与以功率密度最大为目标的优化结果类似,也是SRC构型的系统体积和质量最小,冷却器在换热器体积中占比较大。

图17 以功率质量比最大为目标优化后各构型的体积及质量

不同构型在功率质量比最大作为目标优化后的部件火用损对比如图18所示。结果表明,此优化目标下仍为RHRC构型的火用损最小,SRC构型火用损最大,各构型部件火用损中回热器火用损占比最大,其次是冷却器部件。

图18 以功率质量比最大为目标优化后各构型的部件火用损

3.5 参数优化结果

以发电效率为优化目标,RHRC构型的发电效率最高,可达到47.5%,但相应功率密度和功率质量比分别只有263.47 kW/m3和98.73 kW/t;分别以功率密度和功率质量比为优化目标,RC构型具有最高功率密度282.42 kW/m3和最高功率质量比98.81 kW/t。通过上述优化结果可以看出,以发电效率为目标优化得到的设计方案总体积和总质量较另外两个指标更高,不利于可移动动力系统的灵活部署;以功率密度和功率质量比为优化目标,通过牺牲循环热效率提高了系统紧凑性,因此相应设计方案在适配可移动微型堆方面更具优势。综合以上优化结果,选择RC构型以功率密度最大为目标优化后的结果作为系统的最佳设计方案,RC的最优设计构型及各状态点位置如图19所示(其中1～14为状态点),最优方案下对应各状态点的热力学参数列于表10。

表10 SCO2循环最佳设计方案下各状态点参数

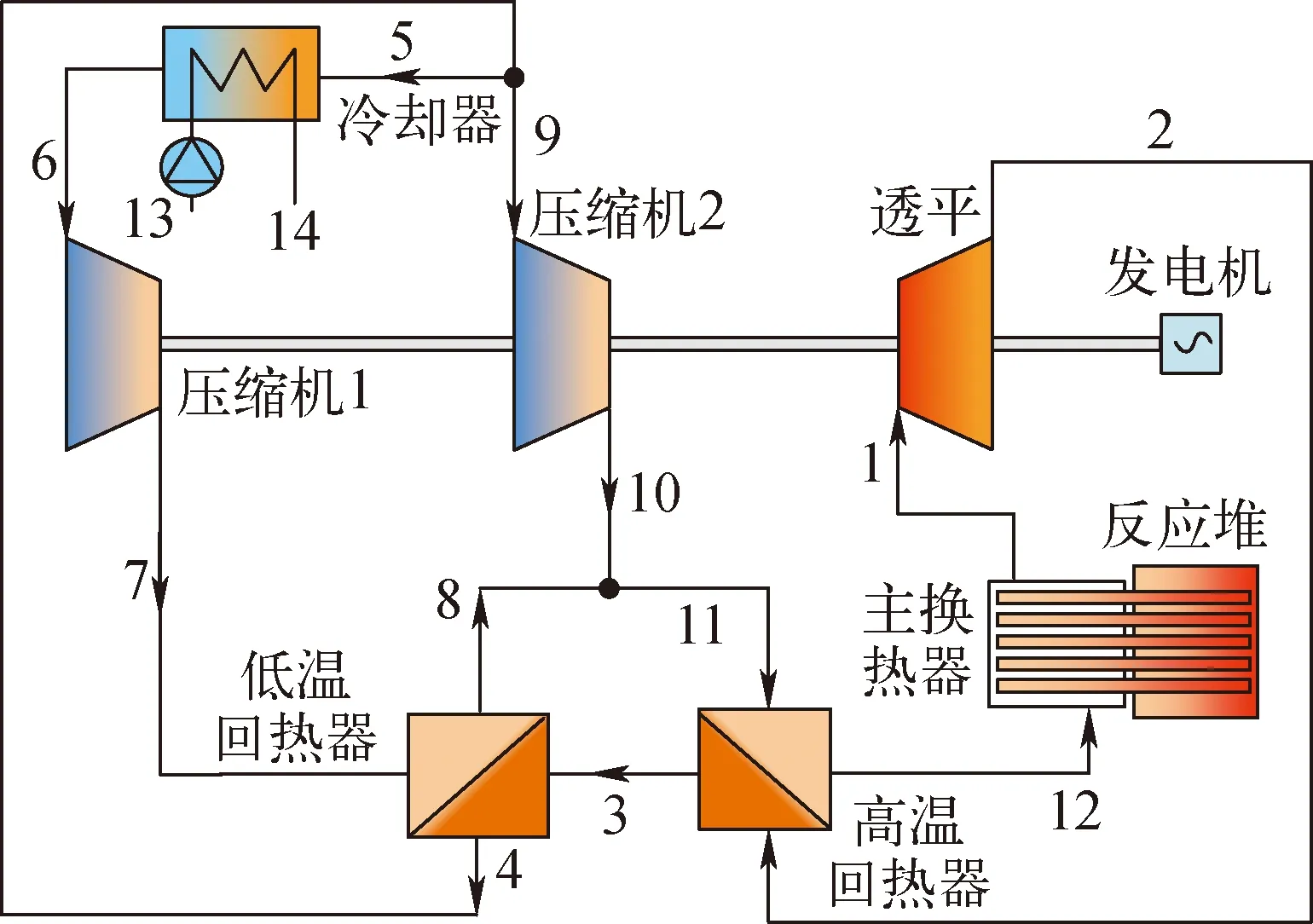
图19 SCO2循环RC构型的最优设计

4 结论

本文以不同构型的SCO2布雷顿循环系统为研究对象,对系统关键部件进行了选型及热力学设计,并开展了不同评价指标下系统不同构型参数优化,获得了不同优化目标下最佳构型及最优参数配置。获得如下主要结论。

1) 对于微型堆SCO2布雷顿循环,系统设计方案为热管反应堆、向心式透平、离心式压缩机、热管管壳式主换热器及再热器、印刷电路板式回热器、扁平翅片管式冷却器较为合理。

2) 以发电效率最大作为优化目标,循环最优构型为RHRC,发电效率最高达47.5%;以功率密度最大作为优化目标,循环最优构型为RC,其功率密度最高可达282.42 kW/m3;以功率质量比最大作为优化目标,循环最优构型也为RC,其功率质量比最高可达98.81 kW/t。

3) 通过不同构型对比发现,RHRC构型具有较高效率,但其系统体积和质量也会较大;RC构型效率接近RHRC构型,且具有较高的功率密度和功率质量比,能较好兼顾高效性和紧凑型,更适合作为可移动微型堆能量转换系统。