低温热阱环境下超临界二氧化碳动力循环概念设计研究

王典乐,黄彦平,殷凯凯,刘旻昀,,周 源,赖相鹏,李 勇

(1.四川大学,四川 成都 610065;2.中国核动力研究设计院,四川 成都 610213;3.清华大学,北京 100084)

超临界二氧化碳(S-CO2)动力循环最早公开发表于1950年Sulzer[1]提交的一篇专利上,并由Feher[2]、Angelino[3-5]、Dostal等[6]进一步研究发展。进入21世纪后,美国、韩国、中国和欧洲等国家和地区相继建立了试验装置,初步验证了S-CO2动力循环技术在工程上应用的可行性[7]。相比蒸汽朗肯循环,S-CO2布雷顿循环系统简单紧凑,设备较少,易于模块化;相比氦气、氮气等类理想气体布雷顿循环工质,S-CO2具有真实气体性质,通过合理布置设计,可有效降低压缩机压缩功耗[5],在中等温度下(550～650 ℃)即可达到较高效率,同时由于密度较大,可减小涡轮机械设备体积,使系统紧凑。由于以上特点,S-CO2动力循环在核能、太阳能、余热回收等领域具有广阔的应用前景[8]。

在常温热阱环境下(约25 ℃),S-CO2动力循环通常将压缩机入口(循环冷端)工质参数设置在临界点附近的超临界状态类液区,以利用此处密度大、易压缩的特点,减少压缩功耗,提高循环效率[9]。在低温热阱条件下,可以利用环境低温特性,对循环冷端进行优化,将循环冷端温度和压力设置在临界点以下,以实现更高的循环效率和更低的运行压力。Angelino[3-5]针对气体布雷顿循环的限制,提出了液相压缩燃气轮机循环,液相压缩燃气轮机循环冷端工质为液态,可有效减少压缩功耗,提高循环效率。经对比分析,CO2被认为是循环工质的较佳选择,并提出了CO2冷凝循环。Feher[2]提出了一种整个循环的工质压力都在临界压力以上的无冷凝的液相压缩S-CO2动力循环(Feher循环),相比Angelino[3-5]提出的冷凝循环,Feher循环冷端工质运行在临界压力以上、临界温度以下,无冷凝过程,但系统工作压力较高。Combs[10]研究了Feher循环在15 MW船用动力中的应用,并在Feher循环的基础上设计了再压缩循环,回热器温差更小,提高了循环效率。美国桑迪亚国家实验室Wright等[11]和Conboy等[12]在早期研究基础上对冷凝型S-CO2动力循环进行了设计研究。研究表明,对于液态金属冷却核反应堆,循环冷端温度由305 K降低到295 K,循环效率提高了2.7%;对于压水堆,经过多级再热后,循环效率达到了38.7%。桑迪亚国家实验室开展了初步验证试验,试验结果表明:由于在5～6 MPa压力下饱和状态的CO2液体和气体密度相差较小(密度比约3∶1),设计用于压缩S-CO2的压缩机也可用于压缩液体、气体和两相CO2;设计用于冷却S-CO2的冷却器,也可用于冷凝气态CO2。设备在运行于两相状态时,未发现有明显的不稳定现象,无需增加汽水分离器或进行额外的设备改造等。近年来,在桑迪亚国家实验室研究基础上,欧洲各国对基于CO2混合工质的跨临界循环进行了大量研究[13-15],以适配于聚光太阳能发电等高温热阱应用。中国核动力研究设计院Jiang等[16]对应用于低温热阱的跨临界CO2布雷顿循环和跨临界CO2朗肯循环进行了热力学分析,研究表明跨临界S-CO2循环具有明显的效率优势。

现有研究已基本验证S-CO2动力循环冷端优化构型的可行性,但相关命名和概念等混淆不清,缺乏较为系统和全面的研究分析。本文针对低温热阱(4～15 ℃)应用环境,对应用于核反应堆热源的S-CO2动力循环进行冷端优化,对已有研究进行归纳整理,并在此基础上提出了3种冷端优化构型概念设计,分析其热力学特性,探索低温热阱应用环境下的最优S-CO2动力循环。

1 S-CO2动力循环冷端优化

简单回热循环示意图如图1所示,其温熵图如图2a所示。低温低压下的工质首先进入压缩机进行绝热压缩,然后依次进入回热器、核反应堆等压升温,进入透平绝热膨胀做功,做功后的工质进入回热器和冷却器等压冷却,并最终进入压缩机绝热升压完成闭式循环。CO2临界点为7.38 MPa、31 ℃,常规S-CO2循环压缩机入口参数常设置于略大于临界点参数处的超临界状态类液区,循环整体都处于超临界状态[6]。

图1 简单回热循环

a——常规S-CO2动力循环;b——Feher循环;c——冷凝型S-CO2动力循环;d——气相压缩S-CO2动力循环

根据热力学第二定律,提高循环增温比将有利于提高循环效率。核反应堆热源出口温度一般是固定的,因此可以根据热阱的不同适当调整循环冷端温度以提高效率。在低温热阱应用环境中(4～15 ℃),可以考虑突破临界点,将循环最低温度设置在CO2临界温度以下,以追求更加优秀的循环性能[17-20]。基于上述考虑,根据冷端工质压缩状态的不同,对常规S-CO2动力循环有以下3种冷端优化方案。

1) Feher循环:将冷端工质参数设置在临界压力之上、临界温度之下,温熵图如图2b所示。循环冷端工质处于可压缩液体状态,可压缩液态工质首先进入压缩机升压;然后进入回热器和核反应堆升温;进入透平膨胀做功;进入回热器初步冷却,并进入冷却器继续冷却至临界温度以下;再进入压缩机升压完成闭式循环。在这种循环中,循环整体压力保持在临界压力之上,冷却器中工质温度降低至临界温度之下。

2) 冷端冷凝型液相压缩S-CO2动力循环:将冷端工质参数设置在临界压力之下、临界温度之下,温熵图如图2c所示。循环冷端工质为液态,液态工质首先进入压缩机升压进入超临界状态;然后依次进入回热器和核反应堆升温;进入透平做功后,工质从超临界状态进入过热气态;过热气态工质进入回热器冷却后成为气态,并进入冷却器发生冷凝相变成为液态;液态工质进入压缩机升压为超临界态完成闭式循环。相比于常规动力循环,此循环冷端工质状态为液态,工质在冷却器中发生了冷凝相变过程,因此可以将此循环称为冷端冷凝型液相压缩S-CO2动力循环,简称冷凝型S-CO2动力循环。

3) 气相压缩S-CO2动力循环:将冷端工质设置在临界压力之下、临界温度之上,温熵图如图2d所示。循环冷端工质处于气态,气态工质首先进入压缩机升压进入超临界状态;然后依次进入回热器和核反应堆升温;进入透平膨胀做功后成为过热气态;进入回热器和冷却器冷却为气态;最终进入压缩机升压进入超临界态完成闭式循环。在这种循环中,循环冷端压力降低至临界压力之下,循环冷端温度也降低至临界温度之下,但大于工质临界温度。

在以上3种冷端优化方式中,热源(核反应堆)处工质仍处于超临界状态,保持了核反应堆堆芯内工质无相变、固有安全的特点。透平入口处也为超临界状态,密度较大,保持了透平体积小、紧凑的特点;压缩机入口处工质为液态或密度较大的气态,保持了压缩功耗较低的特点。

对3种冷端优化方式进行初步分析,3种冷端优化方式均降低了循环最低温度,第1种优化方式(Feher循环)未降低循环压力,压缩机入口为密度较大的液态,压缩功耗较低;第2种优化方式(冷凝型S-CO2动力循环)降低了冷端循环压力,相比第1种优化方式,提高了系统压比,具有进一步提高效率、降低系统压力和系统成本的潜在优势,但需要评估冷凝器中CO2气液两相流动压降对循环效率的影响;第3种优化方式(气相压缩S-CO2动力循环)压缩机入口为密度相对较小的气态,压缩功耗相对较大。在相同的热源温度下,冷端优化后的S-CO2动力循环最低温度更低、最低压力更小,有利于进一步提高效率,降低设备重量,具有高效安全紧凑的特点。本文建立热力学模型,分别对以上3种S-CO2动力循环冷端优化方案进行分析比较。

2 热力学模型

2.1 循环模型

对简单回热循环和再压缩循环建立热力学分析模型,简单回热循环和再压缩循环构型示意图如图3所示。再压缩循环在简单回热循环的基础上增加了再压缩机和低温回热器,循环在低温回热器的热侧出口进行分流,一部分进入冷却器和主压缩机,另一部分直接进入再压缩机,两部分支流在高温回热器冷测进口汇合进入高温回热器。再压缩循环可以减小回热器夹点问题影响,提高循环效率,但系统相对较复杂。

a——简单回热循环;b——再压缩循环

热力学模型程序流程图如图4所示。程序首先输入设计电功率、压缩机进口压力和温度、压比、透平进口温度和回热器端部温差,并假设质量流量初始值,进行迭代计算发电效率,当相对误差小于δ(1%)后,计算并输出发电效率。

图4 热力学程序流程图

2.2 子模型

在压力计算模型中,本文对循环工质流动阻力进行了简化计算,参照文献[11],假设回热器、冷却器和热源总压降为最高压力的5%。通过压缩机入口压力和假设压降,计算循环各设备进出口压力。

压缩机和透平使用等熵模型。根据压缩机效率ηc,计算压缩机功耗Pc为:

(1)

式中:hosc为压缩机等熵出口比焓,kJ/kg;hic为压缩机入口比焓,kJ/kg;m为质量流量,kg/s。

压缩机实际出口比焓hoac为:

(2)

根据透平效率ηT,计算透平实际输出功PT为:

PT=(hiT-hosT)·m·ηT

(3)

式中:hiT为透平入口比焓,kJ/kg;hosT为透平等熵出口比焓,kJ/kg。

透平实际出口比焓hoaT为:

(4)

在换热器设计中,换热器端部温差为重要的输入参数,决定了换热器的基本性能。本文对回热器和冷却器等换热器模型进行了简化,忽略换热器内部复杂的流动换热,假设换热器端部进出口温差为一常数,并根据能量守恒计算换热器进出口温度。获取回热器出口温度参数后,根据质量流量和进出口比焓计算冷却器和热源功率,并计算电功率和循环发电效率。

其中循环发电效率η计算公式为:

(5)

式中:ηe为发电机效率,取常数值为97%;QH为反应堆热源功率。

2.3 模型验证

为验证热力学模型的准确性,使用与桑迪亚国家实验室相同的热力学输入参数[11]对计算结果进行了验证,计算输入参数如表1所列,计算结果如表2所列。桑迪亚国家实验室计算的发电效率为45.5%,本文程序计算结果为45.7%,相对误差约为0.5%。回热器、冷却器等系统设备功率计算结果基本一致,最大相对误差为1.02%,基本验证了热力学模型的准确性。

表1 桑迪亚国家实验室设计参数

表2 模型验证计算

3 热力学特性分析

MIT文献[6]中论证了S-CO2动力循环适配的反应堆出口温度为550～650 ℃;目前常见的压水堆核电站出口温度约为330 ℃,设计15 ℃的换热温差,则循环最高温度为315 ℃。本文分别对透平入口温度为550 ℃和315 ℃的S-CO2动力循环冷端优化构型进行了热力学特性分析。

循环热力学设计参数如下:设计循环电功率为100 MW,根据文献[11]推荐,假设再压缩机效率为87%,透平效率为90%,发电机效率为97%,循环最大压力(主压缩机出口压力)为20 MPa。设计循环回路总共有5%的压降损失,平均分布在回热器、热源和冷却器中,设计回热器端部温差为10 ℃。在较深的湖泊和海洋中,液态水的最低温度为4 ℃左右,设计13 ℃的换热温差,则压缩机入口最低温度为17 ℃左右。

3.1 550 ℃透平入口温度计算

3.1.1简单回热循环 设计透平入口温度为550 ℃,对压缩机入口温度范围为17～47 ℃、压缩机入口压力范围为5.5～8.0 MPa的简单回热循环进行计算,计算结果如图5所示。由图5可见,随着压缩机入口温度降低,发电效率呈先上升后下降的趋势。这是因为在入口温度较高时,循环增温比越大,越有利于增加循环效率,且随着压缩机入口温度的降低,压缩机入口密度增加,压缩机功耗减小;当入口温度较小时,再进一步降低入口温度会造成回热器两侧温差增大,回热能力不足,系统废热增加,引起循环效率的下降。

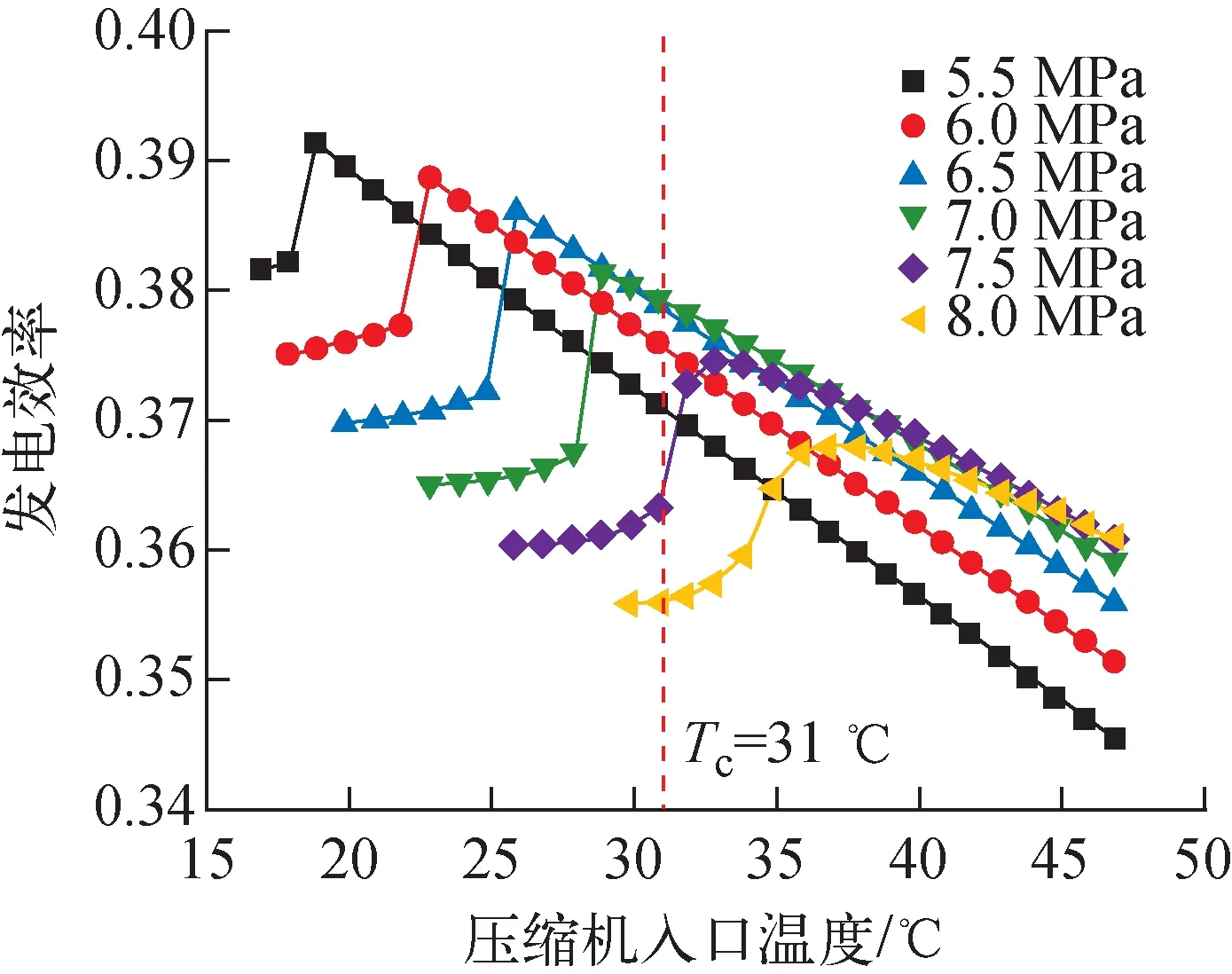
压缩机出口压力为20 MPa

在不同的压缩机入口压力下,存在一个使效率最高的最佳压缩机入口温度。根据入口压力的不同,最佳压缩机入口温度点如表3所列。其中入口压力为7.5 MPa和8.0 MPa时,最佳压缩机入口温度大于临界温度,压缩机入口工质处于超临界状态类液区,为常规S-CO2动力循环,温熵图如图2a所示;压缩机入口压力小于7.0 MPa时,最佳压缩机入口温度低于临界温度,稍大于饱和温度,压缩机入口工质状态处于气相区,为气相压缩S-CO2动力循环,温熵图如图2d所示。其中气相压缩S-CO2动力循环相比常规S-CO2动力循环效率提高了2%～3%。

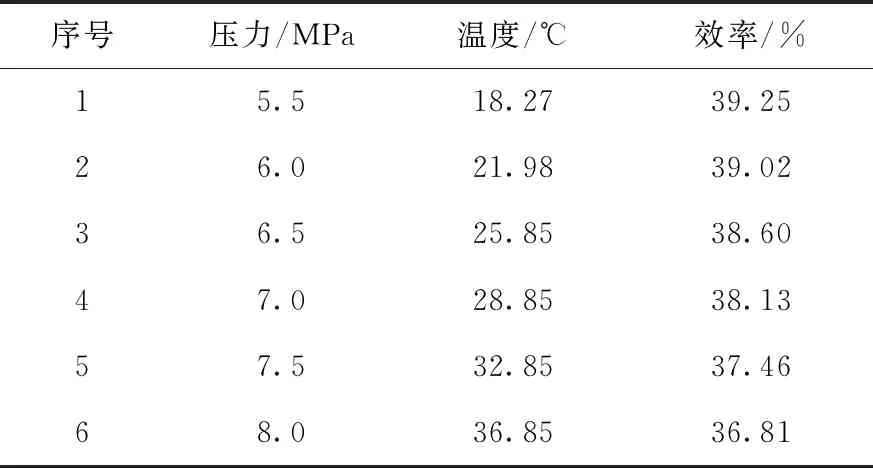
表3 最佳压缩机入口温度点

选取压缩机入口压力为6.0 MPa,入口温度分别为21.85、21.98和22.85 ℃ 3个典型工况进行分析,结果如图6所示,其中:QR为回热器功率,W;QC为冷却器功率,W。压缩机入口温度为21.85 ℃时压缩机入口工质状态为液态,压缩功耗较小,由于在冷却器中发生了气液相变,冷却器废热功率较大,进而引起了热源入口焓下降,热源功率上升,质量流量下降,透平功率下降,这些原因共同造成了循环整体效率降低;当压缩机入口温度为21.98 ℃和22.85 ℃时,压缩机入口工质状态为气态,压缩功较大,但冷却器和热源功率较小,透平输出功较大,效率相对较高。

压缩机入口压力为6.0 MPa

3.1.2再压缩循环 使用与3.1.1节中简单回热循环相同的设计参数,计算再压缩循环的发电效率,如图7所示。计算结果表明,随着主压缩机入口温度降低,循环效率先上升后缓慢下降,存在一个最佳主压缩机入口温度点。主压缩机入口压力大于临界压力时,最佳主压缩机入口温度点位于超临界类液区,为常规S-CO2动力循环,温熵图如图2a所示;主压缩机入口压力小于临界压力时,最佳主压缩机入口温度点处于液相区,循环为冷凝型S-CO2动力循环,温熵图如图2c所示。

压缩机出口压力为20 MPa

根据主压缩机入口压力的不同,再压缩循环的最高效率在44%～48%之间,高于简单回热循环。与简单回热循环不同的是,再压缩循环拥有高温回热器和低温回热器两个回热器,回热能力较强,当循环冷端(主压缩机入口)工质处于温度较低的液态时,由于再压缩循环的分流和两级回热,冷却器废热功率较小,同时液相工质的压缩功耗较小,提高了循环整体效率。相比常规S-CO2再压缩动力循环(44%),冷端冷凝型S-CO2再压缩动力循环效率(48%)提高了4%左右。

3.2 315 ℃透平入口温度计算

3.2.1简单回热循环 设计参数与3.1节一致,透平入口温度为315 ℃,对压缩机入口温度范围为17～47 ℃、压缩机入口压力范围为5.5～7.0 MPa的简单回热循环效率进行计算,计算结果如图8所示。计算结果表明,在相同的压缩机入口压力下,随着压缩机入口温度的降低,循环效率先逐渐上升,后近似保持不变。循环最佳压缩机入口温度点处于液相区,为冷凝型S-CO2动力循环,温熵图对应图2c。

压缩机出口压力为20 MPa

由于循环温差较小,简单回热循环回热器回热效率较高,循环冷端的冷凝过程并没有显著增加废热,同时压缩机压缩液相显著减小了压缩机功耗,从而提高了循环效率。当压缩机入口温度已经低于饱和温度后,压缩机功耗的降低不再显著,循环效率同时受回热器回热能力、循环增温比的影响,效率变化不明显。由于压水堆热源温度较低,循环最高效率为28%,低于蒸汽朗肯循环。

3.2.2再压缩循环 保持透平入口温度为315 ℃不变,其余参数与简单回热循环相同,对主压缩机入口温度范围为17～47 ℃、主压缩机入口压力范围为5.5～8.0 MPa的再压缩循环进行计算,结果如图9所示。在相同的主压缩机入口压力下,循环效率随主压缩机入口温度的降低先迅速升高,达到一个“拐点”后,效率随温度的降低继续缓慢升高。当主压缩机入口压力大于临界压力时,效率变化趋势的“拐点”位于超临界区的类液区;当主压缩机入口压力小于临界压力时,效率变化趋势的“拐点”位于液相区。

压缩机出口压力为20 MPa

在“拐点”前循环效率快速增加,这是由于随着温差的增大,循环增温比增加,同时主压缩机入口工质密度的增加、主压缩机功耗降低,循环效率增加。当到达“拐点”后,主压缩机入口工质密度变化不明显,主压缩机功耗变化不大,循环效率随循环增温比的增大而缓慢增加。同时由于压水堆出口温度较低,再压缩循环回热效率较高,因此在17～47 ℃的温度范围内,主压缩机入口温度越低,循环效率越高,循环温差的增大对回热器的回热能力没有明显影响。

相比简单回热循环,S-CO2再压缩循环能将发电效率最高提升到33%,与现有的压水堆核电站蒸汽朗肯循环相当。由于S-CO2动力循环具有紧凑性的特点,可以降低设备重量、体积和成本等,压水堆耦合S-CO2动力循环具有很好的应用前景,但由于S-CO2再压缩循环的主气系统工作在高温高压区域,其体积重量的优化还需要进行更加深入的设计分析工作。

4 结论

本文搭建了简单回热循环和再压缩循环设计分析程序,对低温热阱应用的S-CO2动力循环进行了冷端优化设计研究,提出了3种冷端优化构型概念设计,并对其热力学特性进行了初步对比分析。基于本文计算模型和简化方法得到的结论如下。

在100 MW规模发电机组下,根据热源温度和循环构型的不同,循环有不同的最佳冷端优化方式。对于透平入口温度为550 ℃的中高温反应堆热源,简单回热循环构型下气相压缩S-CO2动力循环效率最高,为39%,再压缩循环构型下冷凝型S-CO2动力循环效率最高,为48%;对于透平入口温度为315 ℃的中低温反应堆热源,无论是简单回热循环还是再压缩循环,冷凝型S-CO2动力循环效率均最高,其中简单回热循环构型最高效率为28%,再压缩循环构型最高效率为33%。在最高温度和压力相同的情况下,相比常规S-CO2动力循环,冷端优化后的S-CO2动力循环效率提高了2%～4%。冷端优化后的S-CO2动力循环在低温热阱环境应用下具有较好的应用前景。

本研究为低温热阱应用环境下的能量转换系统设计提供了参考。在计算中,本文对回热器和冷却器的压降进行了简化假设,对回热器进行了端部温差假设,在进一步的研究中,应补充完整的换热器模型,针对循环构型开展多目标优化工作。