小型氟盐冷却高温堆SCO2布雷顿循环冷端特性研究

许家源,赵全斌,*,孙剑锋,刘秀婷,张大林,卓文斌

(1.西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049;2.中国华能集团公司,北京 100031;3.中国核动力研究设计院,四川 成都 610213)

核电因其环保、高效、低碳、清洁的特点具有一定的发展潜力,在能源结构体系中扮演的角色也愈发重要。美国橡树岭国家实验室(ORNL)、桑迪亚国家实验室(SNL)及加州大学伯克利分校(UCB)基于已有的第4代堆型(熔盐堆、高温气冷堆、钠冷快堆)进行技术融合再创新,首次提出世界第1个氟盐冷却高温堆(FHR)概念[1-2]。氟盐冷却高温堆融合了熔盐堆、高温气冷堆和钠冷快堆等第4代先进核反应堆的优点,具有高温低压运行、无水冷却、固有安全、结构紧凑等特点。同时,建成体积小、轻量化、低成本的模块化小型氟盐冷却高温堆,可在干旱地区实现高效发电,输出700 ℃以上高温工艺热还可用于高温制氢、盐水淡化、矿藏开采等,特别契合我国西部新丝路沿线偏远地区多用途、多层次能源需求。

为满足小型氟盐冷却高温堆能量转换需求,需要开发与高温氟盐堆的高温、高紧凑性、无水冷却等特征相匹配的能量转换循环系统。结构紧凑、效率高、适用性广、环境友好的超临界二氧化碳(SCO2)布雷顿循环成为优先考虑的目标。

美国阿贡国家实验室的Moisseytsev等[3-4]开发了以第4代核反应堆(铅冷快堆、钠冷快堆等)为热源的SCO2布雷顿循环瞬态仿真平台(PDC),分析研究了变负荷过程(阶跃变化和斜坡变化)以及多种事故工况下(反应堆散热故障、反应堆紧急停堆、发电机故障、管道泄漏、过载)系统中关键参数的动态响应规律。西安交通大学的Wu等[5-6]基于超临界水冷堆的仿真模型SCTRAN,开发了SCTRAN/CO2仿真模型用于研究SCO2循环动态特性、控制策略及事故分析。Oh等[7]研究了SCO2直接冷却反应堆(MMR)简单回热系统的控制策略。

但是分析发现,SCO2布雷顿循环冷端运行在临界点附近,因此SCO2布雷顿循环系统对于冷端参数十分敏感,严重影响循环系统性能,探究动态过程中冷端参数特性成为了SCO2布雷顿循环系统安全稳定运行的关键。同时,当冷端参数跨过临界点时,液化工质会严重威胁压缩机乃至循环系统的安全。

目前针对SCO2循环冷端特性的研究还较少,为此本文针对小型氟盐冷却高温堆SCO2布雷顿循环系统,建立动态仿真模型,开展在冷端扰动下系统的动态特性研究,探究变负荷过程中冷端参数变化,为系统安全稳定快速变工况运行提供理论基础。

1 模型建立

本文以小型氟盐冷却高温堆SCO2布雷顿循环系统为研究对象,采用Matlab/Simulink软件作为仿真平台,内嵌Refprop[8]的接口来计算物性,建立动态仿真模型,系统整体模型如图1所示。该系统主要包含主压缩机、再压缩机、预冷器、储罐、透平、氟盐堆、熔盐-CO2换热器、高温换热器、低温换热器,其中主压缩机、再压缩机、预冷器中工质SCO2接近临界状态,属于冷端范围。SCO2工质在压缩机中进行等熵压缩,在低温换热器、高温换热器、熔盐-CO2换热器中进行等压加热,之后进入透平进行等熵膨胀,最后通过高温换热器、低温换热器、预冷器进行等压放热形成闭式循环。由于主压缩机入口温度、压力为系统最低温度和压力,为防止SCO2退出超临界状态,其入口温度必须大于30.98 ℃,入口压力必须大于7.38 MPa。在建模过程中,对各组件采用能量守恒、质量守恒进行建模,之后组合形成整个闭式循环系统。

图1 系统模型

1.1 氟盐冷却高温堆

本文采用点堆动力学模型来描述堆芯裂变功率变化[9],并考虑各种反馈效应引入的反应堆,点堆方程[10]表示如下:

(1)

(2)

Q=N(t)Qdesign

(3)

式中:N(t)为相对中子数量;ρ(t)为反应性,pcm;Λ为瞬发中子每代的时间,s;β为6组缓发中子总份额;λi为第i组缓发中子衰变常量,s-1;Ci(t)为第i组缓发中子先驱核相对数量;βi为第i组缓发中子份额;Q为换热量,MW;Qdesign为额定换热量,MW;t为时间。

在上述方程中,堆芯裂变功率的主要影响因素是总反应性ρ(t),包含由控制棒等引入的显式反应性以及其他氟盐温度导致的反馈反应性。任意时刻,总反应性方程如下:

(4)

1.2 换热器

印刷电路板式换热器(PCHE)相比于传统换热器具有效率高、紧凑性强等特点。在氟盐冷却高温堆SCO2布雷顿循环系统中,预冷器、高温换热器、低温换热器、热端换热器均采用直通道逆流布置的PCHE。

本文采用有限体积法来建立换热器的一维动态模型,如图2所示。首先将换热器沿流动方向划分为n个控制单元,之后使用能量守恒、质量守恒对每个控制单元内的冷流体、热流体和金属壁面进行建模。

图2 换热器有限体积模型

质量守恒方程为:

(5)

式中:A为流体通流面积,m2;ρ为流体密度,kg/m3;m为质量流量,kg/s;z为换热器通道长度。

热流体侧能量守恒方程为:

αhπDh(Twh-Tf1)

(6)

式中:Ah为热侧流体通流面积,m2;ρh为热侧流体密度,kg/m3;hh为热侧流体比焓,J/kg;ph为热侧流体压力,Pa;mh为热侧流体质量流量,kg/s;αh为热侧流体对流换热系数,W·m-2·K-1;Dh为热侧通道直径,m;Twh为热侧壁面温度,℃;Tf1为热侧流体温度,℃。

冷流体侧能量守恒方程为:

(7)

式中:Ac为冷侧流体通流面积,m2;ρc为冷侧流体密度,kg/m3;hc为冷侧流体比焓,J/kg;pc为冷侧流体压力,Pa;mc为冷侧流体质量流量,kg/s;αc为冷侧流体对流换热系数,W·m-2·K-1;Dc为冷侧通道直径,m;Twc为冷侧壁面温度,℃;Tf2为冷侧流体温度,℃。

金属壁能量守恒方程为:

αhπDh(Tf1-Twh)+αcπDc(Tf2-Twc)

(8)

式中:cpw为壁面比热容,J/(kg·K);ρw为金属壁密度,kg/m3;Aw为金属壁截面积,m2。

工作流体的物理性质对传热系数的计算有很大影响。对于工质水:

(9)

式中:Nu为努塞尔数;Re为雷诺数;Pr为普朗特数。

文献[11]将Gnielinski关联式[12]、Dittus-Boelter关联式和Jackson关联式同实验进行对比,发现Gnielinski关联式与实验结果更加吻合。另外由于换热器中SCO2工质在正常工作区间内雷诺数位于13 510～30 600之间,处于湍流状态,因此本文对于SCO2工质采用Gnielinski关联式:

(10)

式中,f为范宁摩擦系数。

1.3 压缩机

因为涡轮机械的容量较小且质量流量较大,因此相比于换热组件来说响应速度更快,其响应时间几乎可以忽略不计,通常将透平和压缩机的静态模型应用于动态模型中。

本文采用一维均线法设计压缩机几何参数并预测其性能[13],同时省略了多级压缩机中复杂的级间计算,主要研究单级离心式压缩机。离心式压缩机一维平均流线设计将其分为叶轮、扩压器、蜗壳3个部分,如图3所示,从压缩机入口到出口,沿着子午面设置了6个节点(1～6),节点1～6分别代表叶轮入口、叶轮出口、扩压器入口、扩压器出口、蜗壳入口以及蜗壳出口。

图3 离心式压缩机结构示意图

性能预测模型仅是在设计模型的基础上稍加修改即可。在已知边界条件下,可根据完善的损耗模型[14-16]预测压缩机的性能。应用质量连续性、能量守恒和损耗方程来求解压缩机每个节点的速度三角形和热力学参数。通过迭代法,获取压缩机的性能模型,图4为主压缩机性能曲线,主压缩机额定转速为44 398 rpm。

1.4 透平

本文采用单级径向透平进行建模,除结构参数外,模型输入参数为工质入口温度、入口压力、入口流量;输出参数为工质出口温度、出口压力、出口流量、透平功率。利用弗留盖尔公式计算脱离设计工况后的透平背压:

(11)

式中:pout为透平出口压力,MPa;pd,out为透平出口额定压力,MPa;min为透平入口质量流量,kg/s;md,in为透平入口额定质量流量,kg/s;Tin为透平入口温度,℃;Td,in为透平入口额定温度,℃;pin为透平入口压力,MPa;pd,in为透平入口额定压力,MPa。

透平效率、实际出口比焓和透平功率为:

(12)

hout=hin-ηtbΔhi

(13)

wt=ηtbminΔhi

(14)

式中:ηtb为透平效率;ηtb,design为透平额定效率;ρin为透平入口密度,kg/m3;ρd,in为透平入口额定密度,kg/m3;hout为透平实际出口比焓,J/kg;hin为透平入口比焓,J/kg;Δhi为透平理想比焓差,J/kg;wt为透平功率,W。

1.5 阀门

阀门在系统中主要用于控制,通过改变流动面积来控制流量和压力。对于阀门中存储的流量和能量可以忽略不计。阀门开度fopen定义为阀门开口面积与总面积之比:

(15)

式中:Aopen为阀门开口面积,m2;Atotal为阀门总面积,m2。

阀门两端压降Δpv[17-18]为:

(16)

式中,Kv为阀门损失系数。

由于阀门的响应需要一定的时间,阀门的动态特性可采用一阶惯性元件建模:

(17)

式中:τ为与执行机构相关的时间常数;A为当前阀门开度;Ad为设定阀门开度。

2 模型验证

透平模型被广泛使用,准确度较高,本文着重对压缩机和换热器进行仿真验证。

2.1 压缩机模型验证

SNL对SCO2布雷顿循环回路和压缩机进行了多次实验。为确保其验证的可靠性及准确性,采用由SNL发布的数据来完成验证工作[19]。SNL与本文压缩机设计工况列于表1。考虑到压缩机主要包含转子和扩压器两部分,因此以叶轮出口静压(p2)和扩压器出口总压(p04)为参考性能,与SNL的实验数据进行比较。验证结果列于表2,可以看出,叶轮出口静压最大相对误差仅为-4.20%,扩压器出口总压最大相对误差仅为3.24%,模型结果与实验结果几乎一致,因此本文模型可用于SCO2压缩机性能预测。

表1 SNL与本文压缩机设计工况

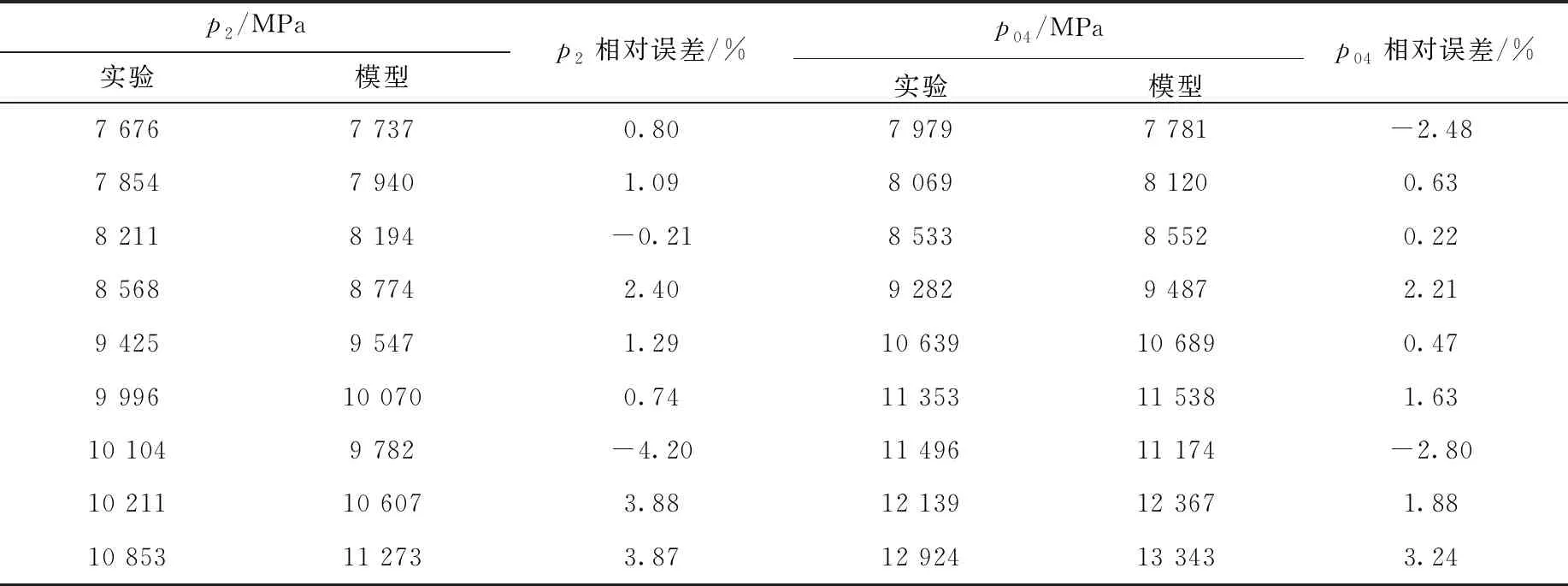
表2 压缩机性能预测程序结果验证

2.2 换热器模型验证

文献[20]用定制的PCHE进行了不同扰动的实验,将实验结果与本文高温换热器、低温换热器模型的计算结果进行对比。当热侧入口温度升高时,两侧出口温度的对比如图5a所示,当热侧入口温度和冷侧入口温度升高时,两侧出口温度的对比如图5b所示,结果表明计算结果的变化趋势基本与实验的一致,稳态相对误差在1%以内。

图5 温度扰动结果的对比

鉴于预冷器的出口温度为31～40 ℃,接近临界点,物性变化非常剧烈,这里采用本课题组搭建的SCO2PCHE的实验数据进行预冷器模型验证。边界输入为预冷器冷侧工质水和热侧工质SCO2的进口温度、压力和质量流量,对比了加热功率扰动下实验和计算的热侧工质SCO2出口温度,如图6所示,发现计算结果和实验结果相吻合,因此预冷器模型可用于后续的仿真研究。

图6 加热功率扰动下实验和仿真结果对比

3 结果与分析

由于本文所研究对象是一种闭式循环系统,系统内部具有很强的耦合特性,尤其是CO2在冷端物性变化剧烈,动态过程复杂多变。本文重点研究冷却水流量扰动下系统的动态响应特性,同时探究变负荷过程中冷端参数的变化。

3.1 冷端扰动下系统动态特性

在t=750 s时,给预冷器处冷却水流量施加了±10%、±30%、±50%共6种不同幅度和方向的阶跃扰动,主压缩机入口温度和流量的变化如图7所示。由图7可见:当冷却水流量阶跃升高时,主压缩机入口温度下降,压力上升;冷却水流量阶跃下降时结果相反,但当冷却水流量阶跃下降-50%时,由于冷却水流量下降造成主压缩机入口温度升高至39.5 ℃,之后工质流量受压力影响下降至39.066 kg/s,由于工质降低的影响更大,因此温度开始下降最后稳定在35.45 ℃。

图7 主压缩机入口状态的变化

透平入口温度的变化如图8a所示,当冷却水流量阶跃下降-50%时,透平入出口温度先大幅升高,在扰动后114 s时达到最高温度683.88 ℃,之后开始下降,在扰动后391 s时下降到最低温度636.23 ℃,最后在扰动发生1 450 s后保持稳定。引起透平温度升高主要有两方面原因:1) 进入氟盐-CO2换热器的CO2流量大幅下降(图7b);2) 冷却水流量降低后主压缩机出口温度升高,通过换热器传递到透平入口,进而引起透平出口温度升高。

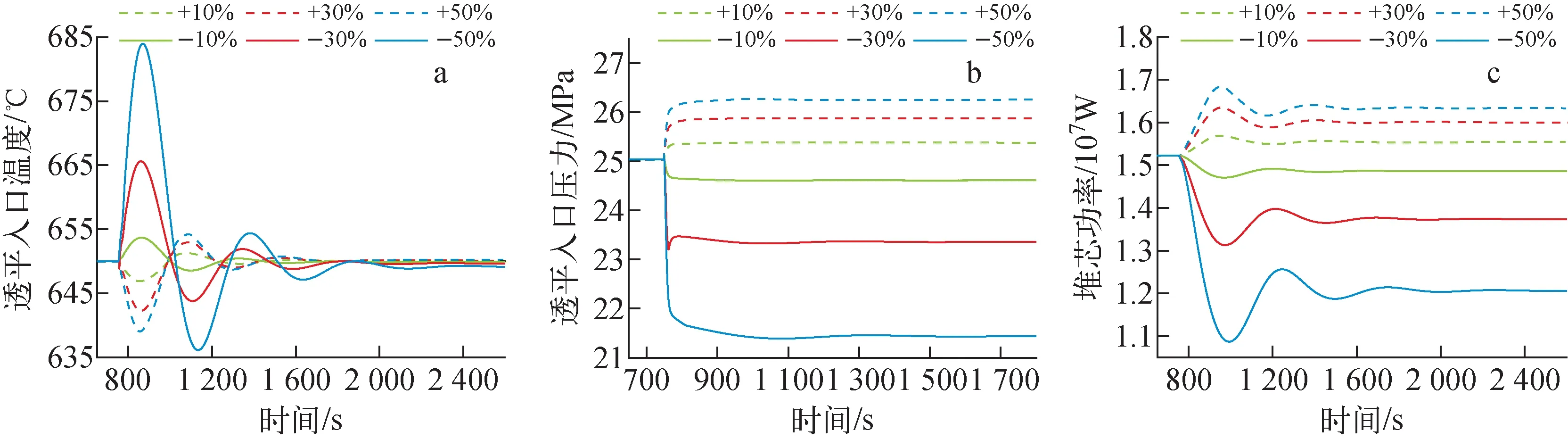
图8 透平入口状态及堆芯功率的变化

透平温度后下降的原因是堆芯功率(图8c)下降导致的,当冷却水流量下降时,堆芯功率受氟盐温度升高的负反馈影响持续下降,之后的波动则是由于换热器温度的滞后性导致,氟盐与堆芯相互影响进而影响整个系统,直至稳定。

综上,当冷却水参数发生变化后,严重影响循环的正常运行,因此保证预冷器出口温度的稳定是运行控制工作中的重点之一;其次,由于堆芯侧热惯性的作用以及堆芯与换热器之间相互影响,导致系统热端波动明显,进而影响冷端,造成冷端有较长时间的波动。

3.2 变负荷下主压缩机入口温度敏感性分析

固定预冷器冷却水入口温度及流量,在透平入口处增加节流阀,通过调节节流阀开度改变透平入口压力及系统质量流量,获得不同负荷下冷端主压缩机状态,结果列于表3。由表3可看出,随着系统负荷的降低,冷端主压缩机出入口压力、流量和温度均在下降,同时效率也在下降。特别值得注意的是在30%负荷以下,发现主压缩机入口处退出超临界状态。

表3 变负荷下主压缩机的状态

将主压缩机单独从系统中取出,固定不同负荷下主压缩机入口压力、流量和转速,探究不同负荷下主压缩机本身对入口温度的敏感性,如图9所示。

图9 变负荷下主压缩机的温度特性

图9a为主压缩机出口压力对入口温度的敏感性。可以看出在降负荷过程中,变负荷点(不同负荷下系统稳定后参数)逐渐从各自特性曲线的平缓区域移动到剧烈波动的区域,主压缩机出口压力对入口温度的敏感性越来越强。这也意味着对主压缩机的控制越来越难,对主压缩机入口温度的要求也越来越高,尤其是在30%负荷下,主压缩机入口温度扰动1 ℃,出口压力变化最高7 MPa。

图9b为主压缩机效率对入口温度的敏感性。在降负荷过程中,主压缩机效率对入口温度的敏感性越来越强。可以看出,在30%负荷下基本不存在效率平缓区域,整体来说变化都较为剧烈,此时在主压缩机入口温度扰动1 ℃的情况下,效率最高变化6.82%。

相比来说,主压缩机入口温度对出口温度的影响较小,在仿真过程中发现主压缩机入口温度扰动0.1 ℃,出口温度变化最高8 ℃,几乎可以忽略不计。

主压缩机出口的波动主要是受CO2物性的影响。图10为不同负荷下固定主压缩机入口处的CO2压力,其温度对密度的影响。这与图9a主压缩机入口温度对出口压力的影响一致。在温度扰动1 ℃的情况下,密度最高变化262 kg/m3。

图10 变负荷下CO2密度与温度变化的关系

3.3 变负荷下主压缩机入口压力敏感性分析

将主压缩机单独从系统中取出,固定不同负荷下主压缩机入口温度、流量和转速,探究不同负荷下主压缩机本身对入口压力的敏感性,如图11所示。

图11 变负荷下主压缩机的压力特性

图11a为主压缩机出口压力对入口压力的敏感性。与图9a类似,可以看出在降负荷过程中,变负荷点也是逐渐从各自特性曲线的平缓区域移动到剧烈波动的区域,各自特性曲线的剧烈波动区域也越来越大,波动也越来越剧烈,主压缩机出口压力对入口压力的敏感性越来越强。在30%负荷下,主压缩机入口压力扰动0.1 MPa,出口压力变化最高6.33 MPa。

图11b为主压缩机效率对入口压力的敏感性。在降负荷过程中,主压缩机效率对入口压力的敏感性越来越强。可以看出,在30%负荷下基本不存在效率平缓区域,整体来说变化都较为剧烈,此时在主压缩机入口压力扰动0.1 MPa的情况下,效率最高变化6.23%。

相比来说,主压缩机出口温度受入口压力的影响较小,仿真过程中发现主压缩机入口压力扰动0.1 MPa,出口温度变化最高12.25 ℃,几乎可以忽略不计。因此,SCO2在临界点处物性剧烈变化的影响主要体现在对系统压力的影响。

图12为不同负荷下固定主压缩机入口处的CO2温度,其压力对密度的影响。这与图11a主压缩机入口压力对出口压力的影响一致。在压力扰动0.1 MPa的情况下,密度最高变化228 kg/m3。

图12 变负荷下CO2密度与压力变化的关系

4 结论

本文基于Matlab/Simulink建立了小型氟盐冷却高温堆SCO2布雷顿循环系统,基于冷却水流量扰动探究了系统动态特性,同时研究了变负荷过程中冷端参数变化,所得结论如下。

1) 冷却水流量扰动直接影响主压缩机入口温度,进而严重影响整个系统稳定运行,因此需要施加一定的控制手段保证预冷器出口温度稳定。

2) 由于堆芯侧热惯性的作用以及堆芯与换热器之间相互影响,导致系统热端波动明显,进而影响冷端,造成冷端有较长时间的波动。

3) 在降负荷过程中,主压缩机对入口温度和入口压力的敏感性逐渐增强。低负荷状态下,主压缩机入口温度扰动1 ℃,出口压力变化最高7 MPa,效率变化最高6.82%;主压缩机入口压力扰动0.1 MPa,出口压力变化最高6.33 MPa,效率变化最高6.23%。