铆钉布置对搭接接头强度的影响及优化设计
韩昊兵,徐文涛,卿 华,任柯融,3
(1.郑州大学 力学与安全工程学院,郑州 450000;2.空军工程大学 航空机务士官学校,河南 信阳 464000;3.国防科技大学 理学院,长沙 410008)
为了满足飞机轻量化的需求,铝合金、钛合金、纤维增强复合材料被广泛用于飞机制造中。飞机结构通常通过铆接、胶接、胶铆连接等连接方式进行连接[1-2]。铆接因其连接强度高、操作简单、成本低、紧密性好而广泛应用于飞机制造中[3-4]。因此对铆接接头力学性能进行分析、评估是有必要的。
针对铆接接头强度影响因素的分析,国内外学者展开了大量研究。Hamel等[5-7]通过有限元模拟研究了工艺参数对接头强度的影响,发现铆接工具的几何形状和工艺参数会影响铆接强度。Zhang等人[8]研究了铝合金铆钉的力学性能,并发现了铆钉尺寸对铆接接头有显著影响。Cui等[9]研究了铆钉模具的倾斜角度对铆接质量的影响,发现特定的铆接模具可改善接头的力学性能,有助于铆接结构的工程应用。Skorupa等[10]在恒幅载荷条件下,通过改变生产因素对铆接搭接接头试样疲劳行为的影响进行了试验研究。结果表明,带补偿器铆钉的疲劳性能远优于圆头铆钉和通用铆钉。Aman等[11]通过有限元方法研究了铆钉直径、铆钉长度、挤压力对成型铆钉质量的影响,并发现减小沉头的深度可以使铆钉与孔之间的间隙消失,进而提高铆接的质量。Li等[12-13]研究了边缘距离对铆接接头强度的影响,发现边缘距离对铆接接头的动态疲劳强度和静态性能有显著影响,且随着边缘距离的增加,搭接试样的剪切和剥离强度随之增加。
对于铆接结构荷载分布的研究,人们建立了铆接接头的简化力学模型,认为在板件拉伸或压缩过程中,铆钉通过剪切变形来传递载荷,且每个铆钉都视作均匀荷载[14]。但是连接件的整体强度会因为个别板的“短板效应”而大打折扣,因此在采用铆钉连接时,要量化这种差异。McCarthy等[15-16]研究了配合间隙差异是如何影响螺栓连接构件受载时的应力状况,并测量了每个螺栓传递荷载的大小,是一些学者研究钉传荷载的基础。蒋持平等[17]通过求解静力平衡方程和位移协调方程得到了平面状态下不同位置钉传荷载的解析解。张天宇等[18]通过编写APDL子程序可以快速求解铆接构件的荷载-位移曲线。Gray等[19]通过试验研究了接头厚度、层压板锥度和缺失紧固件对单搭接多螺栓接头载荷分布的影响,并发现缺少紧固件会导致承载能力的重大损失。黄庆概等[20]提出可以通过控制压铆量来控制钉-孔干涉量,从而使得荷载分配更加均匀。
综上所述,学者们对于铆接接头强度影响因素的分析大多都是针对铆钉尺寸和板材厚度的研究,但在实际应用中,铆接接头布置方式对其力学性能的影响也较为显著,改变铆钉的布置方式可以有效提高铆接接头的力学性能,然而目前关于这方面的研究较少。除此之外,对于铆接结构荷载分布的分析主要集中在钉传荷载的均匀性上,且建立力学模型均为一维模型,不能够有效解释各影响因素对铆接搭接接头强度的影响。
本文首先通过试验和仿真研究了铆接构件的破坏机理,然后通过试验讨论了铆钉数量、铆钉行数、铆钉布置、铆钉行距、铆钉边距、铆钉间距对搭接强度的影响。并建立二维力学模型定性说明了各影响因素对搭接强度影响的机理。最后基于响应面算法对铆钉布置进行了优化,得到了设计变量水平的最优组合。研究成果对飞机铆接结构强度的提高具有重要价值。
1 试验与数值模拟
1.1 试验研究
1.1.1 影响因素
当铆接构件承受拉力时,板承受拉力,铆钉承受剪力,板铆钉处承受剪力和挤压力。为了防止板被单独拉坏、挤压坏或剪坏,就要使板的破坏拉力、破坏挤压力、破坏剪力相等。板的破坏拉力P1、破坏挤压力P2、破坏剪力P3表达式如下
P1=(t-d)δ·σb
(1)
P2=d·δ·σ1
(2)
(3)
式中:t、c、δ、d分别为铆距、边距、板厚与铆钉直径;σb、τb、σ1分别为板的抗拉强度极限、抗剪强度极限与抗挤压强度极限;
当铆孔处的破坏挤压力P2等于板边缘的破坏剪力P3时,即:
(4)
对于m行铆钉的铆接件来说,当板的破坏拉力P1等于板的破坏挤压力时,即:
(t-d)δ·σb=m·d·δ·σ1
t=d(1+1.8m)
(5)
可见,铆接构件的搭接强度与铆距和边距密切相关。不仅如此,其搭接强度还和铆钉数量、铆钉行数、铆钉布置、铆钉行距有关,所以需要进行试验对其进行研究。
1.1.2 试验参数及设计
测试板材为2 mm厚的2024-T4铝合金,铆钉为直径4 mm[21]的LY10铝合金圆头铆钉,两板相互有一定的重叠长度,并以铆钉连接,即单搭-剪切。板材试样和铆钉几何尺寸如图1所示,其中c为铆钉边距,a为铆钉行距,t为铆钉间距,W为板材宽度,L为搭接长度。
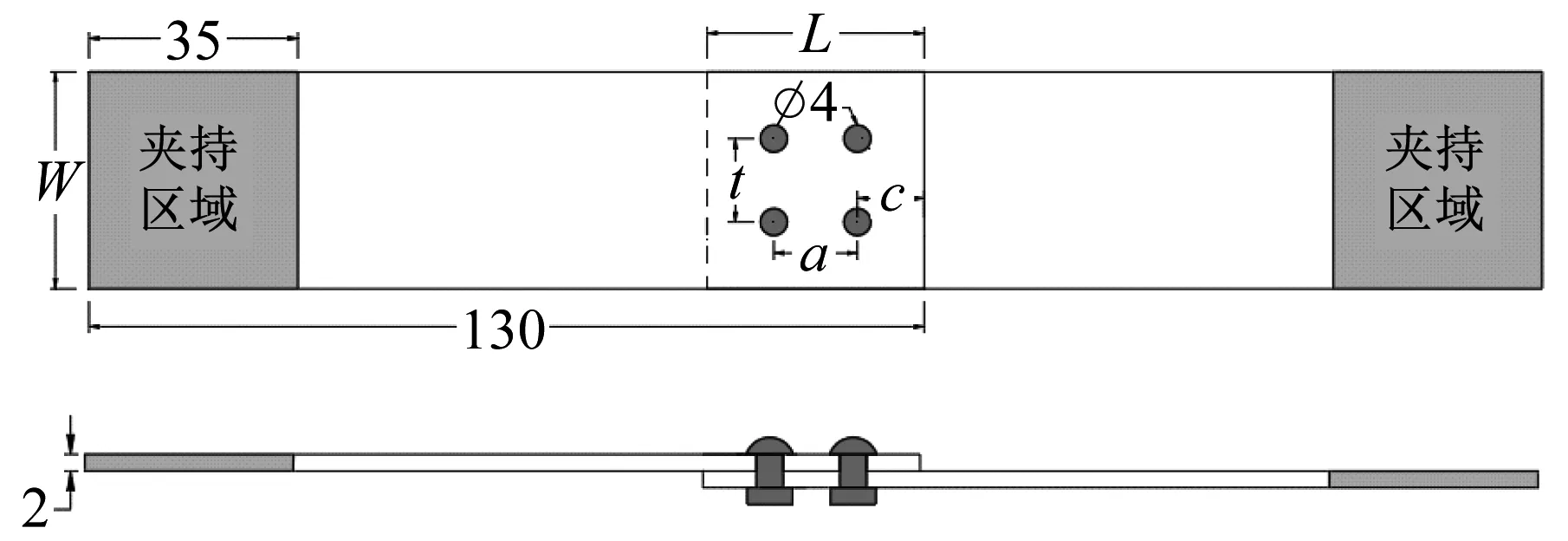
(a) 搭接试样
铆钉布置的标准标签格式如图2所示。例如,试样5-3-122-8-12-10,其中“5”为5个铆钉,“3”为三行铆钉,“122”为从左到右三行铆钉的个数分别为1个、2个、2个,“8”为边距,“12”为铆距,“10”为行距。

图2 铆钉标签格式Fig.2 Label format of rivets
为了分析铆钉数量、铆钉行数、铆钉布置、铆钉行距、铆钉边距、铆钉间距对搭接强度的影响,进行了41组铆接搭接试验,每组3个试样。试验方案如表1所示。

表1 试验方案设计Tab.1 Experimental scheme design
Sun等[22]研究了接头的动态强度随拉伸试验加载速度的增加而增加,并发现当加载速度在0.5~2 mm/min和10~30 mm/min时,其对峰值荷载的影响较为显著,当加载速度在2~10 mm/min时,其对峰值荷载的影响较小。所以该试验使用CMT4304电子万能试验机以3 mm/min的速度进行单向拉伸试验。为消除搭接试样的偏心影响,采用偏心夹头进行试验。
1.2 仿真分析
1.2.1 材料模型
仿真过程应考虑铆钉和板材的应变硬化效应。在拉伸试验中,铆钉和板材都会产生塑性应变,因此使用各向同性弹塑性材料模型。幂硬化本构模型[24]可用于表征其材料特性。
幂硬化本构模型可以表示为
(6)
式中:σy为屈服应力;C和p为Cowper-Symonds常数,对于铝合金C=6 500 s-1,p=4;k、n分别为强度系数和硬化指数;εyp为屈服弹性应变;εp为有效塑性应变。
为了开展高保真的有限元仿真分析,材料参数的准确性是至关重要的。本文对图3所示的犬骨试样进行了准静态拉伸试验与仿真,将试验得到的力-位移曲线和仿真得到的力-位移曲线进行比对,通过自适应模拟退火算法[25]反复调整材料参数、迭代,最终反向标定得到了材料参数。2024-T4铝合金和LY10铝合金的模型参数如表2所示,其中εmax表示失效应变。

表2 幂硬化模型参数Tab.2 Power hardening model parameters
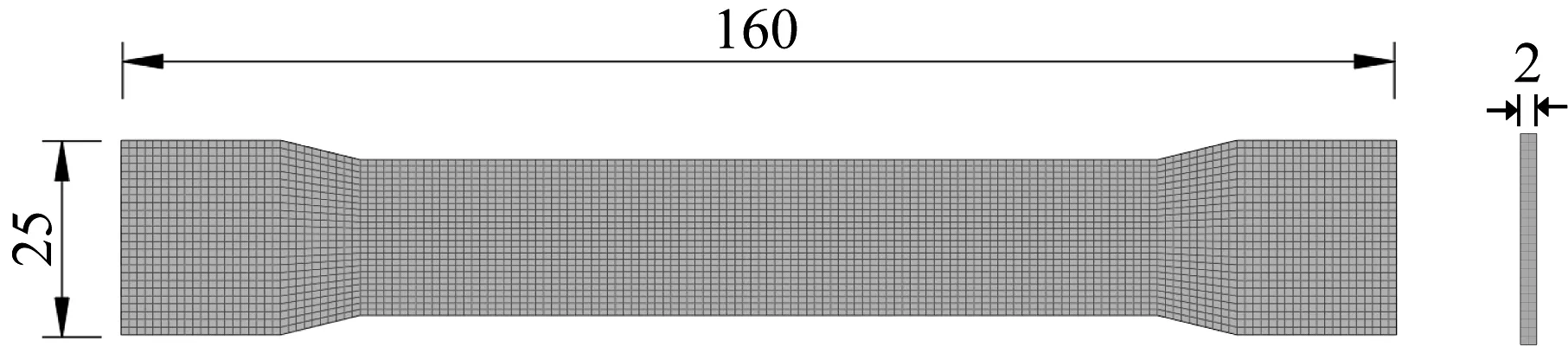
图3 板材有限元模型(mm)Fig.3 Finite element model of plate(mm)
1.2.2 参数设置
在非线性有限元仿真软件LS-DYNA中建立拉伸试验模型。铆钉与板材均采用六面体单元,铆钉和板材搭接处网格大小为0.5 mm,其余部分网格大小为1 mm。模型共42 591个节点,38 752个单元。材料模型[26]使用MAT_POWER_LAW_PLASTICITY;上板与下板,上板与铆钉,下板与铆钉均采用AUTOMATIC_SURFACE_TO_SURFACE的接触方式,摩擦因数取0.18;对基板一侧35 mm使用BOUNDARY_SPC_SET约束其所有自由度,另一侧35 mm约束其Y、Z方向自由度,并使用BOUNDARY_PRESCRIBED_MOTION_SET施加X方向3 mm/min的速度载荷;采用最大主应变随机失效模型,模拟其拉伸断裂过程,使用MAT_ADD_EROSION定义铆钉和板材的失效模式;为模拟其准静态拉伸过程,仿真中使用CONTROL_IMPLICIT_GENERAL隐式求解器进行求解;通过DATEBASE_BINARY_D3PLOT输出动画文件,通过DATEMASE_CROSS_SECION_SET输出力位移曲线,通过CONTROL_TERMINATION设置终止时间为10 s;最后提交作业进行求解。
因为拉伸过程属于大变形,所以使用CONTROL_CONTACT改变默认的接触算法,通过增大SLSFAC来调整滑动接触刚度。在分析中应该使用非线性迭代求解方法,因此使用CONTROL_IMPLICIT_SOLUTION将NSOLVR调整为12,以保证求解收敛。
1.2.3 仿真模型验证
为了验证仿真模型的有效性,建立1颗铆钉搭接试样的有限元模型,如图4所示。将仿真结果与试验结果进行对比,结果如图5所示。仿真曲线与试验曲线拟合良好,相对误差在3%以内,表明所建立模型具有较高的可信度。

图4 铆接搭接接头有限元模型Fig.4 Finite element model of rivet lap joint

图5 试验-仿真力位移曲线对比Fig.5 Comparison of test and simulation curves
2 结果与分析
2.1 单搭-剪切失效行为分析
2.1.1 试验结果分析
试验结果表明,连接件会发生2种基本类型的失效模式:(Ⅰ)铆钉剪切破坏(Ⅱ)板材断裂,且断裂的位置发生在铆钉数量较多的一侧。图6显示了观察到的不同失效模式。
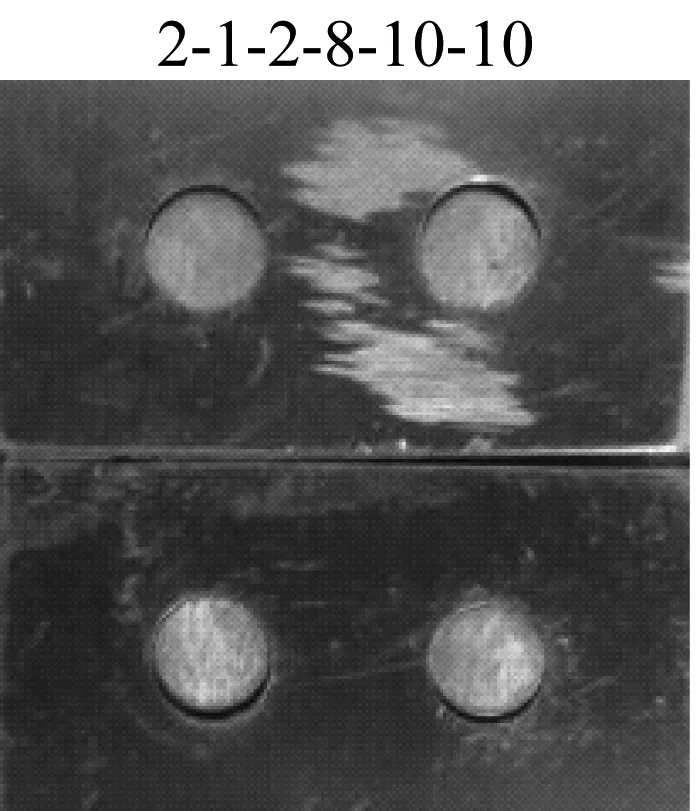
(a) 铆钉剪切破坏
图7为三种铆钉布置形式的力位移曲线对比。由此可知,加载初期,试样处于弹性变形阶段,荷载与位移呈线性关系,此时接头具有较高的刚度,剪力主要由搭接区域的摩擦力和自锁结构传递。随着荷载的增加,试样进入塑性变形阶段,荷载随着位移的增长呈非线性缓慢递增,此时接头刚度下降,板末端发生翘曲变形,搭接区域间隙逐渐增大,摩擦阻力降低,荷载增大到最大值。最终由于达到了板材(铆钉)的强度极限,板材(铆钉)发生剪切破坏,荷载急剧下降。
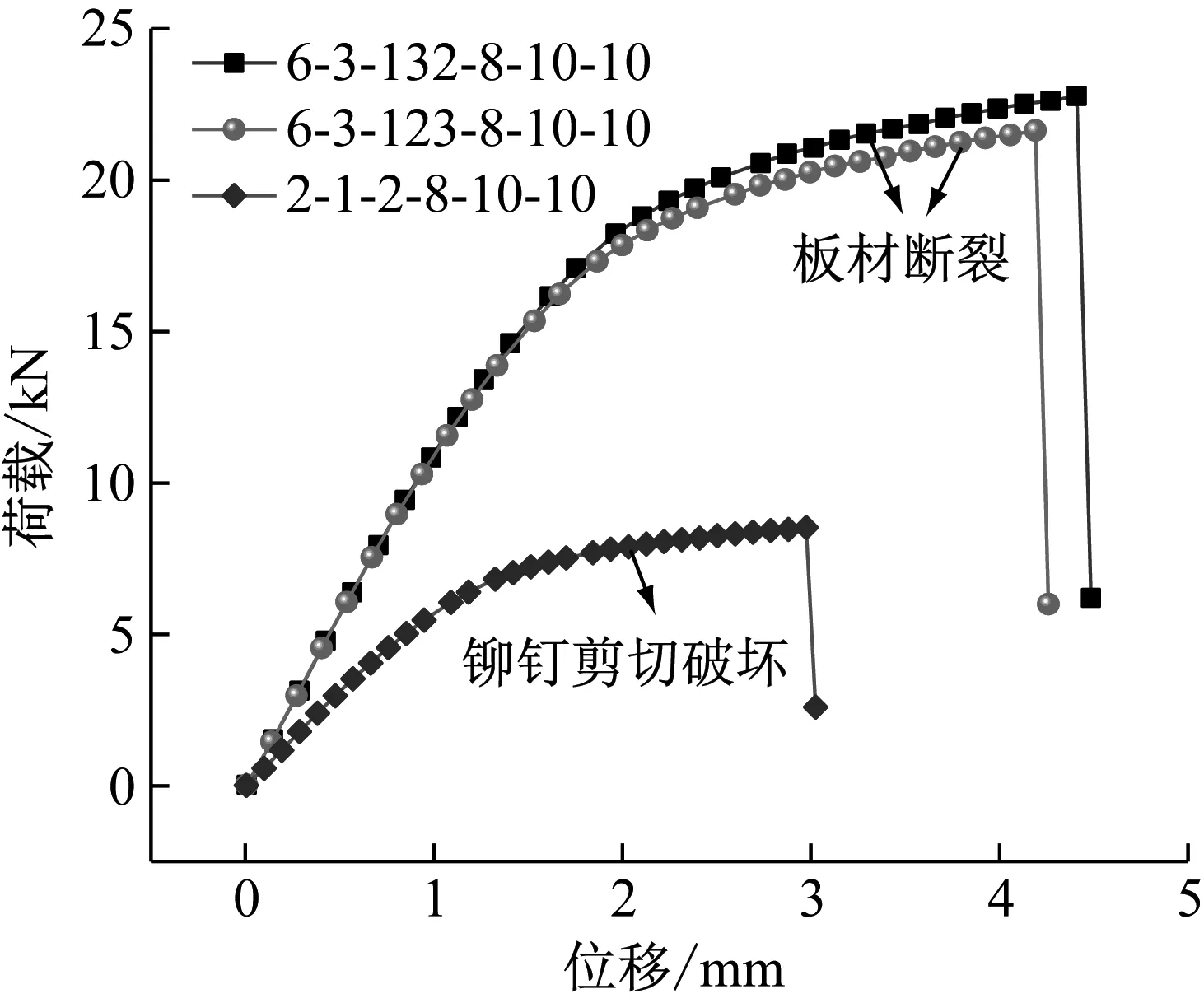
图7 不同铆钉排列形式力位移曲线对比Fig.7 Comparison of force displacement curves of different rivet arrangements
在拉伸过程中,上板铆钉孔壁由于受到铆钉挤压而产生塑性变形,板末端发生翘曲变形,此时剪力主要由自锁结构、上板铆钉孔壁、下板铆接点底部传递。当某一传递环节所承受的强度低于与其竞争的其他环节的强度时,该剪力传递的连接关系将成为试样的薄弱部分,也将首先发生破坏,即“强度竞争”。当上板铆钉孔壁与下板铆接点底部强度大于自锁结构,即板材剩余强度大于铆钉总强度时,发生Ⅰ型失效。相反,当板材剩余强度小于铆钉总强度时,搭接区被铆钉管腿撕裂,发生Ⅱ型失效。而断裂位置发生在铆钉数量较多的一侧主要是因为每个铆钉都会降低板材的有效截面积,当铆钉数量较多时,板材的有效截面积减小,在拉伸过程中,将会产生更大的应力,所以其最先发生断裂。同理,铆钉布置形式为“132”的拉伸强度大于“123”的主要原因为:前者外侧铆钉行的有效截面积大于后者铆钉行的有效截面积。
2.1.2 仿真结果分析
对编号为6-3-132-8-10-10的单搭接接头进行应力分析,定义了行1~行3的位置与各个铆钉的编号,其有限元模型如图8所示。行1至行3周围单元的位移-应力曲线如图9所示,与试验结果相比,仿真破坏位置与试验一致。各个铆钉的钉传荷载如图10所示。可以看出,行1应力大于其他行铆钉处的应力,而行2的应力大于行3的应力。每个铆钉周围都会应力集中,外侧铆钉数量较多一侧的应力集中最为严重。这主要是因为:1、2号铆钉的钉传荷载大于其他铆钉的钉传荷载,进而导致行1的应力严重系数大于其他行的应力严重系数,所以行1的应力集中程度最高,最先发生断裂。通过云图可以看出,随着荷载的增加,行1的应力首先增大,并发生屈服,随后应力集中区域发生扩展,在两颗铆钉周围形成“M”型应力集中区域,其中,两颗铆钉之间应力最大。当主应变达到失效应变时,两颗铆钉之间首先发生断裂,并向外延伸直至整体断裂。

图8 1-3-2有限元模型Fig.8 1-3-2 finite element model

图10 各铆钉钉传荷载Fig.10 The rivet load of each rivet
2.2 铆钉布置规律研究
2.2.1 线荷载集度
由于不同铆距与边距,会导致板材宽度发生变化,而最大承载力等于板材剩余强度极限与横截面面积的乘积,所以不同铆距与边距会导致最大承载力的变化。为了消除板材宽度对最大承载力的影响,本文提出使用线荷载集度来衡量铆距和边距对搭接强度的影响。
搭接强度恢复率为
(7)
式中:η为强度恢复率;F为搭接试样的最大承载力;F1为等宽度完好板的最大承载力;σb为板材的强度极限;S、a、δ分别为板材的横截面积、宽度和厚度。
由于板材的强度极限和厚度保持不变,所以在研究铆距和边距对搭接强度的影响时,使用线荷载集度F/a来衡量其搭接强度。
2.2.2 应力分析
对8-4-2222-8-16-10的试样进行有限元分析。为读取铆钉之间的应力数据,定义2条路径,如图11所示。线1与荷载方向垂直且为板材断裂处,沿y轴方向;线2与荷载方向平行,沿x轴方向。读取不同峰值荷载下板材的应力云图,如图12所示。可以看出,应力集中区域首先发生在外侧两铆钉处,随后应力集中区域向两侧延伸,直至断裂,过程中线1为最危险区域。最终由于线1的应力集中,导致搭接试样发生断裂。
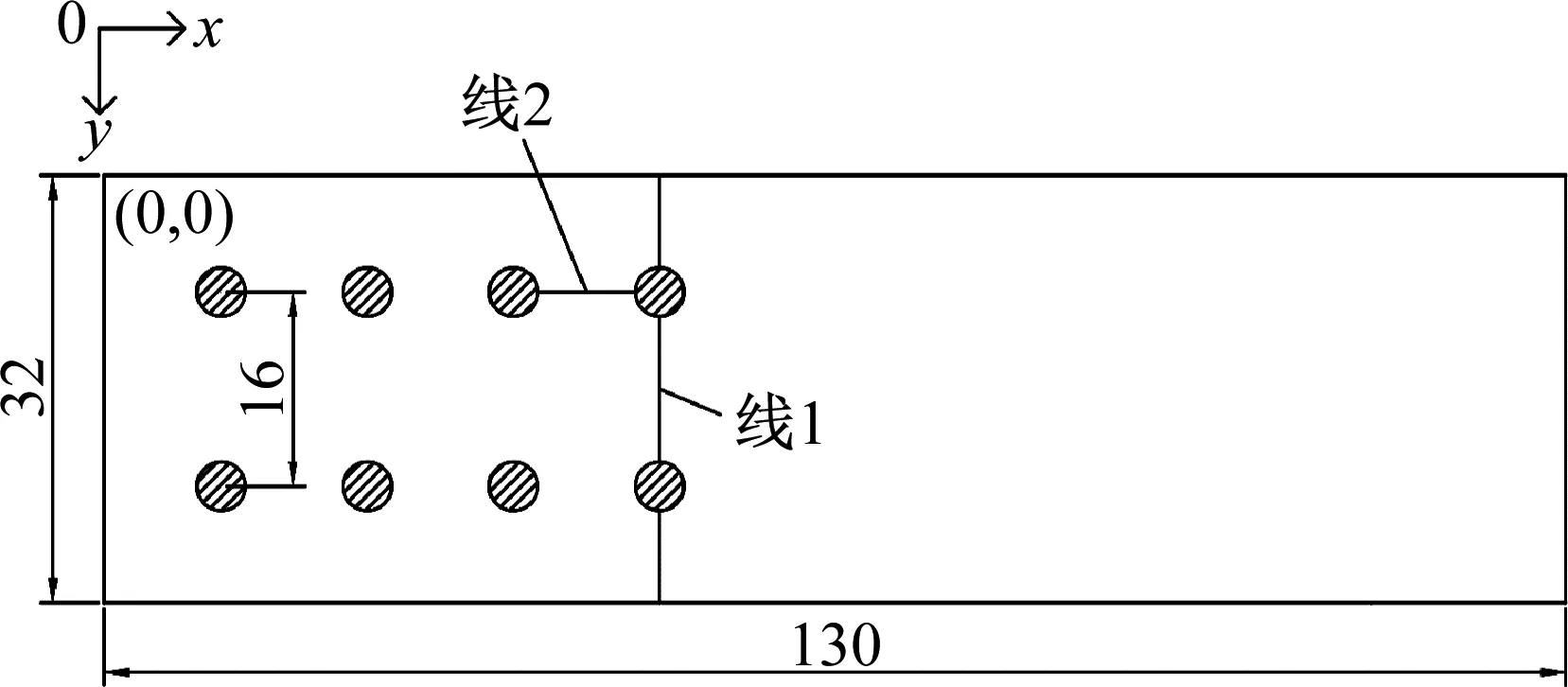
图11 路径定义(mm)Fig.11 The path definition(mm)

35%峰值荷载
由图13可以看出,线1整体为应力集中区,应力均大于430 MPa,铆钉周围2 mm应力大于500 MPa,线1为搭接试样的最危险区域,而线1主要是铆距与边距的方向,即铆距和边距引起了线1的应力集中。由图14可以看出,线2的应力远小于线1的应力,且距离外侧铆钉越远应力越小,而线2为行距方向,即行距不是影响其应力集中的主要因素。
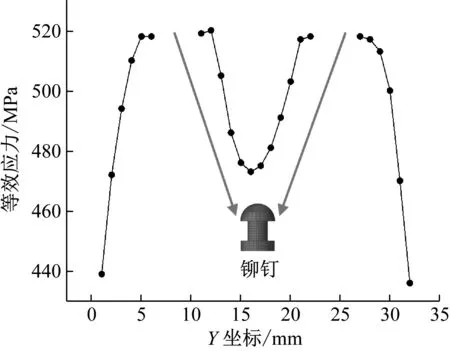
图13 沿线1的应力分布Fig.13 Stress distribution along line 1

图14 沿线2的应力分布Fig.14 Stress distribution along line 2
2.2.3 铆钉数量
对板材尺寸为130 mm×36 mm×2 mm,铆钉数量1-9个的试样进行试验。结果表明:当铆钉数量小于等于4个时,铆钉发生剪切破坏,当铆钉数量大于4个时,板材发生断裂。铆钉数量对峰值荷载的影响如图15所示。对于铆钉数量小于8个的试样,铆钉数量对峰值荷载的影响非常显著,且随着铆钉数量的增加而增加。对于铆钉数量为8~9个的试样,铆钉数量对峰值荷载的影响是有限的。当铆钉总强度小于板材剩余强度时,铆钉发生剪切破坏,且峰值荷载与铆钉数量呈线性关系,即铆钉总强度等于铆钉数量与单个铆钉强度的乘积;当铆钉总强度大于板材剩余强度时,板材发生断裂,此时再增加铆钉的个数,不能够明显增加搭接强度。对比9颗铆钉与7颗铆钉的试样可以得出:当铆钉总强度大于板材剩余强度时,铆钉数量的增加,甚至可能会导致静强度的下降。所以当铆钉总强度大于板材剩余强度时,铆钉数量并不是影响搭接强度的关键,它主要决定了搭接结构的破坏形式。

图15 铆钉数量-峰值荷载曲线Fig.15 Number of rivets-peak load curve
2.2.4 铆钉行数
对边距8 mm,铆距10 mm,行距10 mm,板材尺寸130 mm×36 mm×2 mm,铆钉行数1~4行的试样进行试验,铆钉行数对峰值荷载的影响如图16所示。结果表明:当布置1行铆钉时,铆钉发生剪切破坏,当布置1行以上时,板材发生断裂;当铆钉总强度大于板材剩余强度时,增加铆钉行数不能明显增加搭接强度;3行铆钉的搭接强度最高,但相较于2行铆钉峰值荷载仅提升0.68 kN,而4行铆钉相较于3行铆钉,搭接强度没有提升;从搭接长度的角度分析,增加搭接长度不能明显增加搭接强度。所以当铆钉总强度大于板材剩余强度时,铆钉行数不是影响搭接强度的关键。提高搭接强度,需要改变铆钉的布置形式。

图16 铆钉行数-峰值荷载曲线Fig.16 Rivet row numbers-peak load curve
2.2.5 铆钉布置
对边距8 mm,铆距10 mm,行距10 mm,板材尺寸130 mm×36 mm×2 mm,不同铆钉布置方式的试样进行试验。结果表明:所有试样均发生板材断裂,铆钉布置对峰值荷载的影响如图17所示。对比1-3-2、2-1-3、1-2-3可知,当铆钉数量相同且铆接构件的行数在两行以上时,中间行铆钉数多的构件静强度更高。这主要是因为,硬点效应使得外侧铆钉处的应力远高于其他位置铆钉处的应力,当外侧铆钉多,中间铆钉少时,外侧铆钉的应力集中出现叠加,应力集中程度较高,使得构件的静强度降低;对比1-3-2和3-3-3可知,两者搭接面积相同,铆钉数量却与峰值荷载成反比,所以,铆钉数量的增加不一定会增加搭接强度且多行铆钉应该布置成“中间多两边少”的布置形式;对比3-3-3和3-2-3可知,交错布置和平行布置静强度无明显差别。

图17 铆钉布置-峰值荷载曲线Fig.17 Rivet arrangement-peak load curve
2.2.6 铆钉行距
样本标签6-3-222-8-12-a为对不同行距进行的试验,其中a=2d、2.5d、3d、3.5d、4d、4.5d、5d,板材尺寸为130 mm×28 mm×2 mm,行距和搭接长度对峰值荷载的影响如图18所示。结果表明,行距和搭接长度对峰值荷载的影响有限;由图14也可以看出,沿线2方向应力集中程度不高,不是搭接试样的危险区域,所以铆钉行距对搭接强度的影响有限。
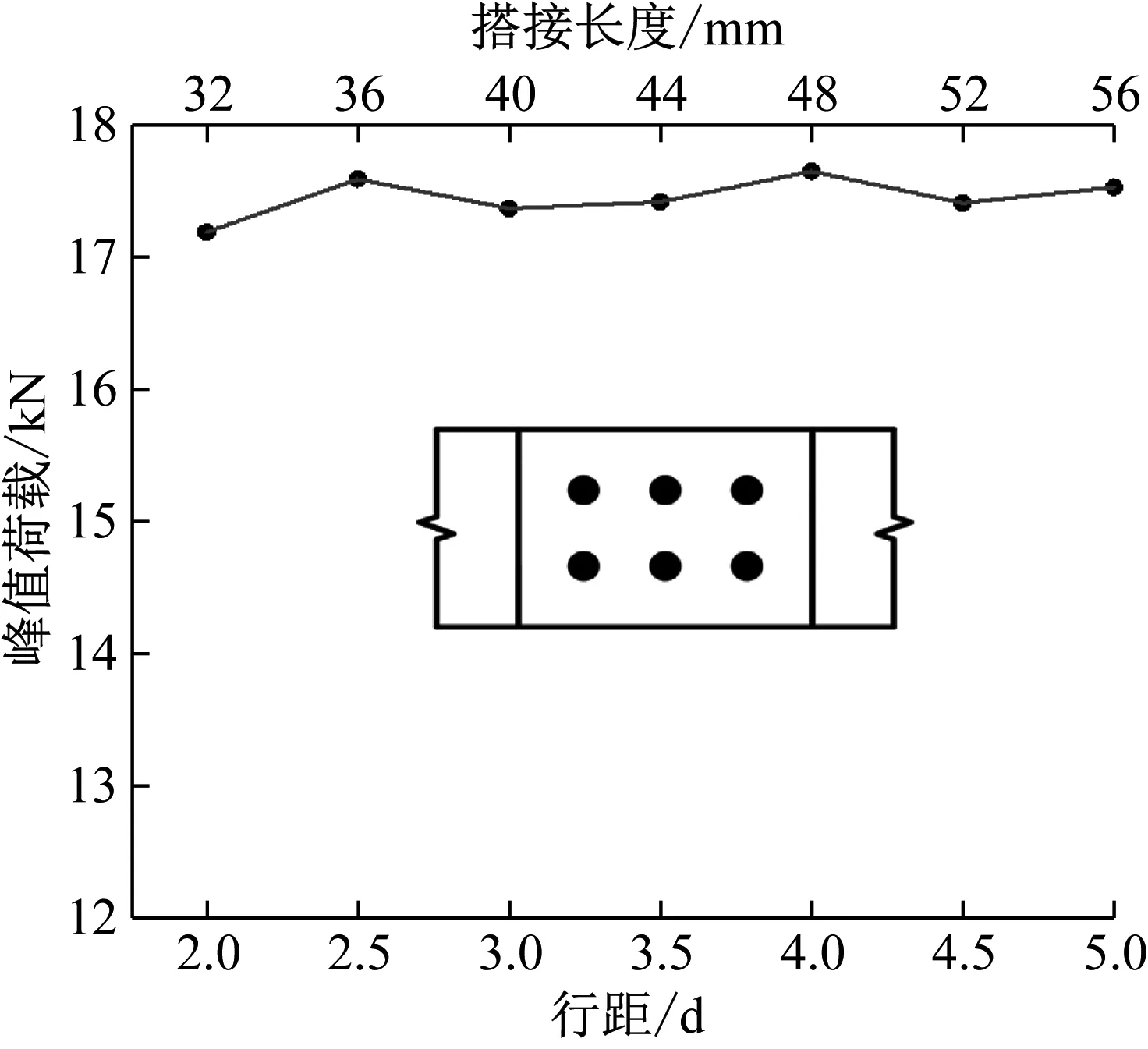
图18 铆钉行距-峰值荷载-搭接长度曲线Fig.18 Rivet row spacing-peak load-lap length curve
2.2.7 铆钉间距
为了消除板材宽度对搭接强度的影响,使用线荷载集度F/a衡量试样的搭接强度。样本标签8-4-2222-8-t-10为对不同铆距进行的试验,其中t=2d、2.5d、3d、3.5d、4d、4.5d、5d、5.5d、6d。板材尺寸为130 mm×Wmm×2 mm,其中W=24、26、28、30、32、34、36、38、40。铆距对线荷载集度和最大应力的影响如图19所示。结果表明:线荷载集度随着铆距的增加而增加,但是,当铆距大于5d时,线荷载集度随着铆距的增加无明显变化;最大应力随着铆钉间距的增大而减小,当t>5d时,减小程度有所降低;由图13可以看出,线1方向铆钉之间应力集中程度最高,为试样的最危险区域,增大铆钉间距是通过减小铆钉之间的应力集中程度来提高搭接强度的。

图19 铆钉间距-线荷载集度-最大应力曲线Fig.19 Rivet spacing-line load density-maximum stress curve
2.2.8 铆钉边距
为了消除板材宽度对搭接强度的影响,使用线荷载集度F/a衡量试样的搭接强度。样本标签8-4-2222-c-12-10为对不同边距进行的试验,其中c=d、1.5d、2d、2.5d、3d、3.5d,板材尺寸为130 mm×W1mm×2 mm,其中W1=20、24、28、32、36、40。边距对线荷载集度和最大应力的影响如图20所示。结果表明:线荷载集度随着边距的增加而增加,但是,当边距大于3 d时,线荷载集度随着边距的增加无明显变化;最大应力随着铆钉边距的增大而减小,当c>3d时,减小程度有所降低;由图13可以看出,铆钉与板边缘之间的应力集中程度很高,为试样的危险区域,增大铆钉边距是通过减小铆钉与板边缘之间的应力集中程度来提高搭接强度的。

图20 铆钉边距-线荷载集度-最大应力关系曲线Fig.20 Rivet end distance-line load density-maximum stress curve
3 讨论
3.1 铆接搭接力学模型
和单钉铆接结构的对称性不同,多钉铆接结构由于每个钉孔所受的荷载不同,所以并不具有对称性。具体每个钉孔所受荷载的大小,与材料属性、铆钉个数、搭接形式等密切相关。根据不同位置处铆钉的受力情况,可以将钉-孔分成三类;首钉:离外荷载最近,受到钉传荷载、旁路荷载和干涉作用力;末钉:离外荷载最远,仅受到钉传荷载和干涉作用力;中钉:位于首钉与末钉之间,同时受到钉传荷载、旁路荷载和干涉作用力,且距离首钉越远,旁路荷载越小。
钉传荷载施加在钉-孔结构上之后,由于孔周干涉挤压变形,钉传荷载会首先释放干涉应变,之后钉孔产生挤压。对于旁路荷载,可以将其看作带孔板的拉伸。钉孔的受力可看作以上三种受力的叠加,如图21所示。其中:Fr为钉传荷载,Fa为旁路荷载,Fint干涉作用力。

图21 铆接孔周应力状态示意图Fig.21 Schematic diagram of stress state around riveted hole
因此,铆接结构应力可表示为
σ=σr+σa+σint
(8)
式中:σr为钉传荷载应力;σa为旁路荷载应力;σint为孔周残余应力。
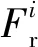
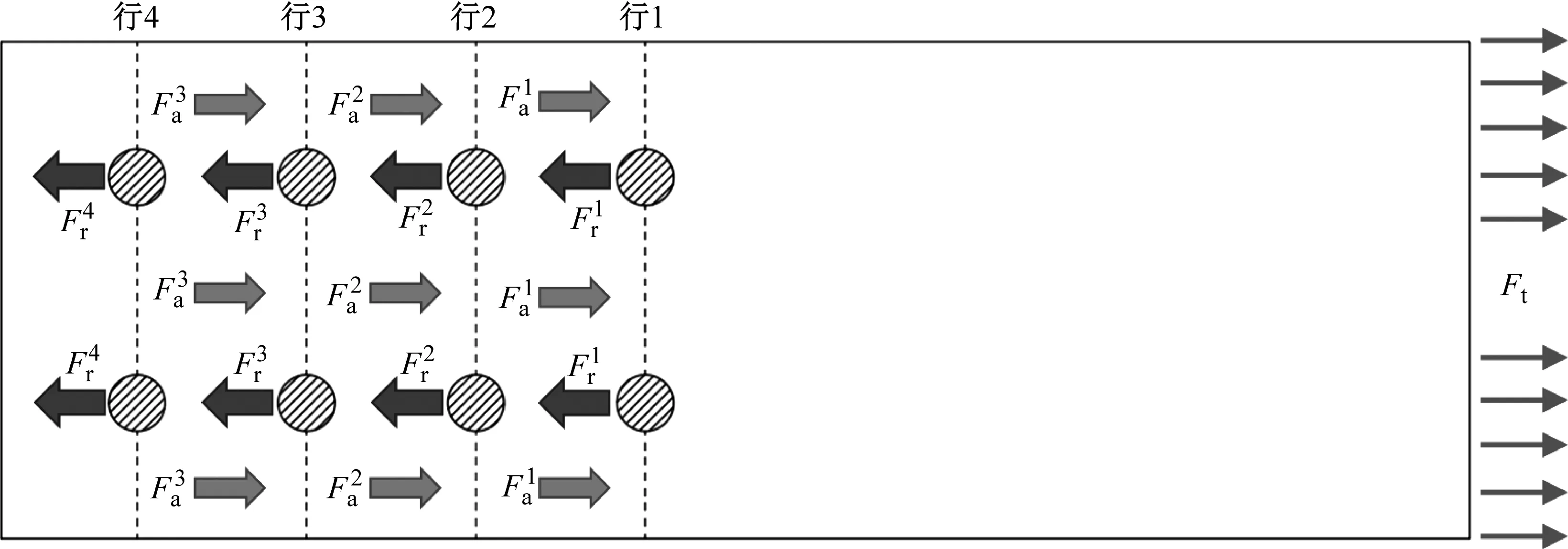
图22 多钉铆接受力示意图Fig.22 Multiple riveting receiving diagram
对于钉传荷载有
(9)
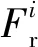
根据旁路荷载的定义,旁路荷载可表示为
(10)
可以看出旁路荷载的计算是以钉传荷载为基础,因此钉传荷载的计算是分析铆接构件荷载分布的关键。
式(9)和式(10)表明,所有钉传荷载的代数和等于板件拉伸荷载Ft,绕过前一个钉孔向后传递的旁路荷载等于其后所有铆钉的外荷载之和,因此最后一个孔周不向后传递荷载。不同位置旁路荷载存在很大差异,这将导致铆接搭接接头不同位置的应力分布具有差异。由于旁路荷载的存在,搭接接头两端铆接孔周围的应力明显大于中间位置。
为了能够定性分析出铆距与边距对搭接强度的影响,可以引入应力严重系数对结果进行解释。
其表达式为
(11)
式中:L为应力严重系数;σ1为旁路荷载引起的孔边局部最大应力;σ2为钉传荷载引起的孔边局部最大应力;α为孔的表面状态系数;θ为紧固件和连接板间的填充系数;σ为危险截面对应的名义应力;Fa为旁路荷载;ΔF为紧固件传递荷载;Kta为旁路应力引起的应力集中系数;Ktb为挤压应力引起的应力集中系数;W为板宽;t为板厚;d为铆钉孔直径。
由于板材与铆钉的强度总是随着应力严重系数的增大而降低,所以应力严重程度对复杂连接件强度的影响系数可写为
β(L)=1-LA
(12)
式中,A为铝合金的材料参数。
考虑应力严重系数的影响,复杂连接件峰值拉伸荷载可写为
F∞=(1-LA)F0
(13)
式中,F0为完好板的峰值拉伸荷载。
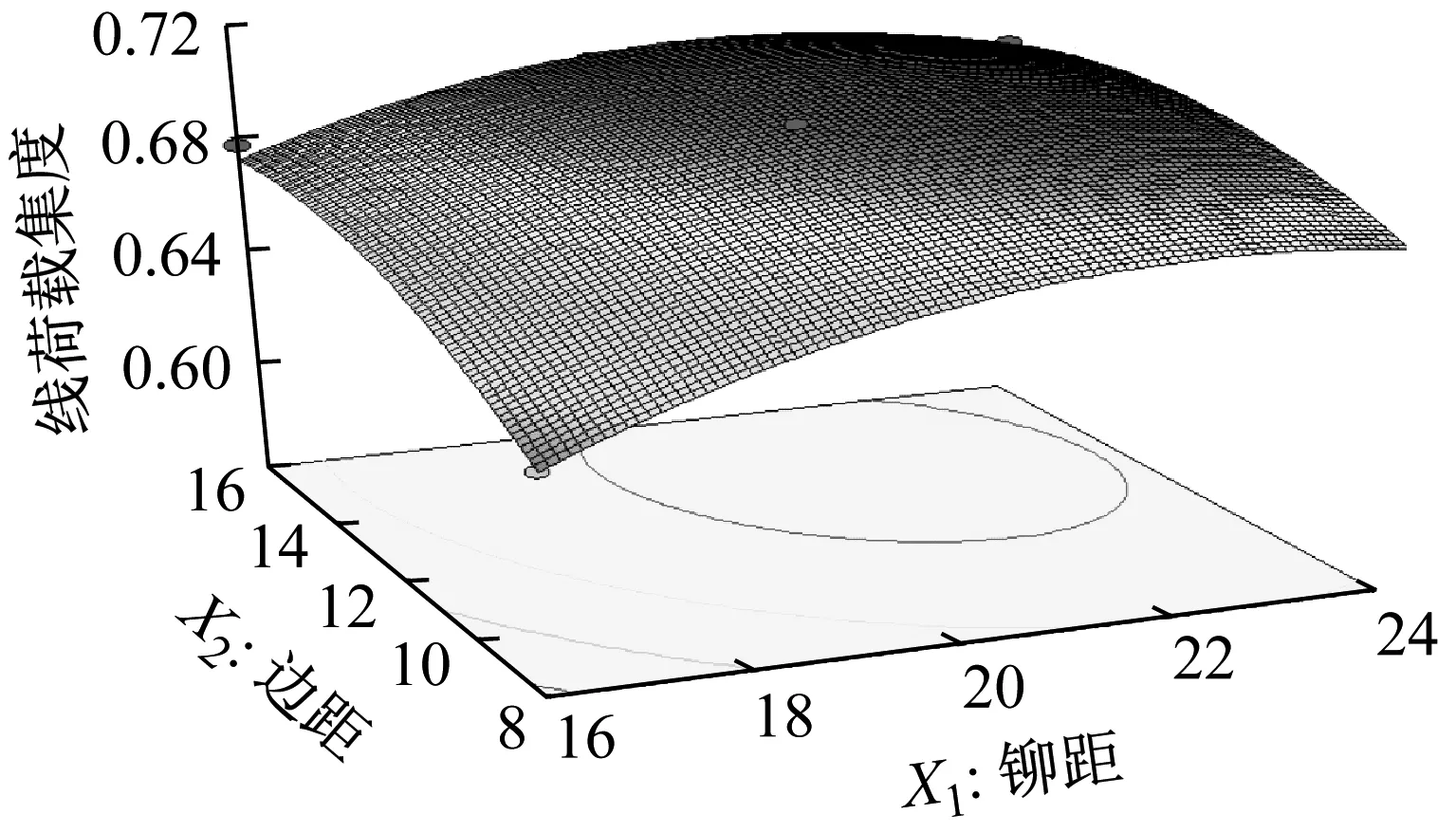
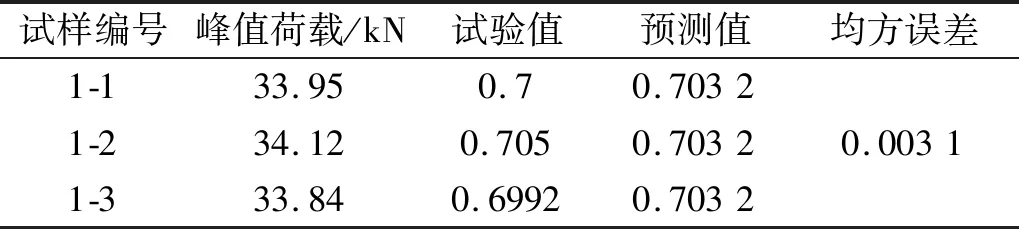
式(13)表明,搭接构件的峰值荷载主要由应力严重系数L决定,L越小,搭接构件的强度越高。图23为8-5-22222-12-24-12搭接构件的拉伸荷载、钉传荷载、旁路荷载的荷载值,可以看出搭接结构中钉传荷载远大于旁路荷载,即ΔF>Fa,且Ktb>Kta[27],d 图23 8-5-22222-12-24-12荷载类型荷载值Fig.23 8-5-22222-12-24-12 load value of load type 提取行1不同铆距与边距时铆钉的钉传荷载占总钉传荷载的比值,如图24所示。可以看出,增大铆距与边距就是减小了钉传荷载的大小,进而减小了应力严重系数,使得构件的应力集中程度更低,搭接强度更高。 (a) 不同铆距钉传荷载占比 3.2.1 响应面法理论 响应面法是基于泰勒展开的理论,泰勒展开一般是基于一个变量,而响应面法是扩展到多个变量进行分析,如下式所示 (14) 式中:Y为响应目标,即为线荷载集度;Xi和Xj分别为模型输入变量;k为输入变量的数量,本文中k=3;βi、βii、βij分别为线性效应系数、二次效应系数和Xi与Xj交互作用的系数;ε为误差项。 3.2.2 BBD试验分析 Box-Behnken Design(BBD)试验是一种基于响应面理论的试验方法,被广泛应用于各种试验当中。为进一步探讨边距、铆距、行距对搭接强度的影响,本文以边距、铆距、行距3个因素为自变量进行编码,编码水平表见表3,BBD设计方案与响应值见表4。为了明确各因素对响应值的影响,使用最小二乘法对表中数据进行回归拟合,得到以线荷载集度为响应值的二次回归方程 表3 BBD设计变量与水平Tab.3 BBD design variables and levels 表4 BBD设计方案及响应值Tab.4 BBD design scheme and response value Y=0.7+0.015X1+0.013X2-0.002 86X3- 0.005 775X1X2+0.009 225X1X3- 0.019X1-0.013X2-0.002 225X3 为检验回归模型的有效性,需要对响应模型进行方差分析。多元相关系数R2可以对响应模型的效果进行评价。R2的取值范围为[0,1],且其越接近1表明拟合效果越好[28],R2可表示为 (16) 式中:Sr为回归平方和;St为总平方和;Se为残差平方和。 同时还需要统计特征值F值,即回归均方与残差均方的比值,其计算公式为 (17) 式中:Mr为回归均方;Me为残差均方;ν为响应模型中变量的个数;n为试验组数。由式(17)可知,残差均方越小,特征值F越大,模型的可靠性越高。当F大于某个特征值F0时,则认为模型有效。通常使用P值表示F 表5是回归方程的方差分析,整体模型显著(P<0.05),对拟合回归方程进行误差统计分析,计算多元相关系数R2=0.963 2,表明此回归方程拟合效果较好。 表5 方差分析Tab.5 Results of variance analysis 根据回归分析结果,得到响应面如图25所示。由响应面图可知,当边距c=13.58=3.4d,铆距t=21.32=5.3d,行距a=13.8=3.4d,响应值达到最大,此时线荷载集度的最大预测值为0.703 2。 (a) Y=f(X1,X2) 3.2.3 试验验证 为了验证预测值的准确性,以边距c=3.4d=13.6,铆距t=5.3d=21.2,行距a=3.4d=13.6,铆钉布置形式为“2-2-2-2-2”的试样进行3组试验,试验的预测值与实测值如表6所示。通过计算,预测值与实测值的均方误差为0.003 1,表明该模型的预测效果较好。对于边距、铆距、行距对线荷载集度的影响具有指导意义。 表6 试验值与预测值对比Tab.6 Comparison of experimental and predicted values 本文首先以最大承载力为指标研究了铆钉数量、铆钉行数、铆钉布置、铆钉行距对搭接强度的影响,针对变化铆距、边距会导致板材宽度发生变化的问题,提出以线荷载集度为指标研究铆距与边距对搭接强度的影响,最后采用响应面法以线荷载集度为响应目标,对铆钉边距、铆钉间距、铆钉行距进行了优化,优化后铆接接头的综合性能显著提高,主要结论如下: (1) 铆接搭接的主要失效形式为铆钉剪切破坏和板材断裂。失效形式遵循“强度竞争”原则。当铆钉总强度小于板材剩余强度时,铆钉发生剪切破坏,此时最大承载力与铆钉数量呈线性关系;当铆钉总强度大于板材剩余强度时,板材发生断裂,且断裂位置发生在铆钉数较多一侧,此时增加铆钉数量与铆钉行数对搭接强度的影响有限。 (2) 当铆钉行数在2行以上时,应遵循中间铆钉数多,两侧铆钉数少的原则;交错布置与平行布置的搭接强度无明显差别。 (3) 对于一定边距和行距的布置方式,铆距是影响搭接接头力学性能的主要因素。搭接强度随着铆距的增加而增加,当铆距t<5d时,搭接强度随着铆距的增大而增大;当t>5d时,搭接强度变化不大;对于一定铆距和行距的布置方式,边距也是影响搭接接头力学性能的主要因素,搭接强度随着边距的增加而增加,当边距c<3d时,搭接强度随着边距的增大而增大;当c>3d时,搭接强度无明显变化;对于一定铆距和边距的布置方式,行距对搭接强度的影响是有限的,从搭接长度的角度分析,搭接长度对搭接强度的影响同样有限。 (4) 通过建立铆接搭接力学模型得出:所有钉传荷载的代数和等于板件拉伸荷载;由于旁路荷载的存在,搭接接头两端铆接孔周围的应力明显大于中间位置;铆距和边距是通过改变钉传荷载的大小改变应力严重系数,从而导致搭接构件的应力集中程度有所不同,进而使得搭接强度有所差异。 (5) 采用响应面法确定最优的铆钉布置方案为:边距3.4d、铆距5.3d、行距3.4d。验证试验的最大承载力为33.97 kN,线荷载集度为0.701 9,与预测值基本相符。

3.2 响应面分析


4 结 论

