混合润滑结合面法向接触刚度模型研究
兰国生,冀成龙,李 祥,李声祺,李 勇,杨 琦
(太原科技大学 机械工程学院,太原 030024)
在整机设备中,由于各部件相互配合导致存在大量的粗糙表面,并且粗糙表面之间相互接触组成结合面,结合面的接触刚度特性在机械设备整机的接触刚度中占据重要地位,有研究[1]表明,机床结合面的刚度约占机床总刚度的60%~80%,结合面引起的变形量约占机床总的静变形量的85%~90%。因此,研究结合面的接触刚度特性对整机性能的分析和预测具有重要的意义。
现今,许多学者对结合面的接触刚度做了大量的研究。杨红平等[2]用分形几何理论表征结合面微凸体参数,建立微凸体由弹性变形向弹塑性变形最终向完全塑性变形转化的各阶段的接触刚度模型;田红亮等[3]基于各向异性分形几何理论,根据法向载荷的连续性和光滑性原理建立固定结合面的法向接触力学模型;李小彭等[4]对MB分形模型进行修正,分析微凸体在弹性、弹塑性和塑性各阶段的变形状态,建立结合面法向接触刚度分形预估模型;张伟等[5]建立综合考虑微凸体基体变形和相互作用的结合面法向接触刚度模型;谭文兵等[6-7]将结合面微凸体等效为椭圆形和锥形,建立了依据各向异性分形理论的结合面法向接触刚度模型;
以上研究中大多基于无润滑介质的结合面接触,而在实际工作中结合面大多处于润滑状态下工作。因此,Gonzalez-Valadez等[8]采用超声反射回波测试方法,并基于界面的超声反射系数与接触刚度之间的关系,试验获得了混合润滑界面的接触刚度。Sun等[9]通过超声弹簧模型和薄膜共振模型推导出了液体刚度表达式,建立了混合润滑结合面法向刚度二维分形模型;肖会芳等[10]基于GW统计模型、油膜共振模型和弹簧模型,推导出固体接触刚度和液体润滑介质接触刚度,提出一种混合润滑状态下粗糙界面法向接触刚度的计算模型;李玲等[11]针对润滑条件下结合面的接触特性受油膜厚度影响的问题,建立混合润滑状态下结合面的法向接触刚度模型。
在以往的研究工作中,研究者大多基于统计学方法建立结合面法向接触刚度模型,而统计学方法不能精确地对粗糙表面进行描述。因此本文基于具有自相似性和尺寸独立性的Weierstrass-Mandelbrot函数和分形理论对粗糙表面形貌进行三维表征,将粗糙表面微凸体等效为锥体建立固体接触的法向接触刚度模型;然后根据固体-液体接触界面油膜共振模型得到液体接触刚度模型,并仿真分析结合面相关参数对结合面法向接触刚度的影响趋势,最后与试验数据进行对比,验证了该模型的准确性。
1 粗糙表面微观形貌三维表征
GW模型是粗糙表面微观形貌的传统表征方法,此模型是基于统计学对粗糙表面微观形貌特征进行定量化的描述,主要的统计学描述参数为高度标准差e,轮廓算术平均值Ra、轮廓高度均方根值σ以及微凸体顶端的平均曲率半径R等,这些参数具有精确度取决于仪器的分辨率的统一特性;基于此特性,使得描述结果不具有客观唯一确定性,即各个参数不具有尺度独立性。而Berry、Majumdar和Ausloos等研究发现Weierstrass-Mandelbrot函数具有自相似性和尺寸独立性,满足粗糙表面微观形貌的分布特征。因此本文采用带有随机变量的双变量W-M函数,该函数的表达式为:
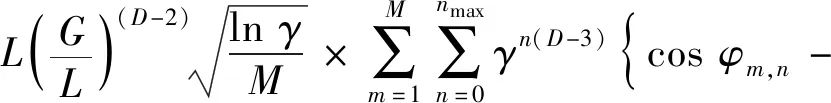
(1)
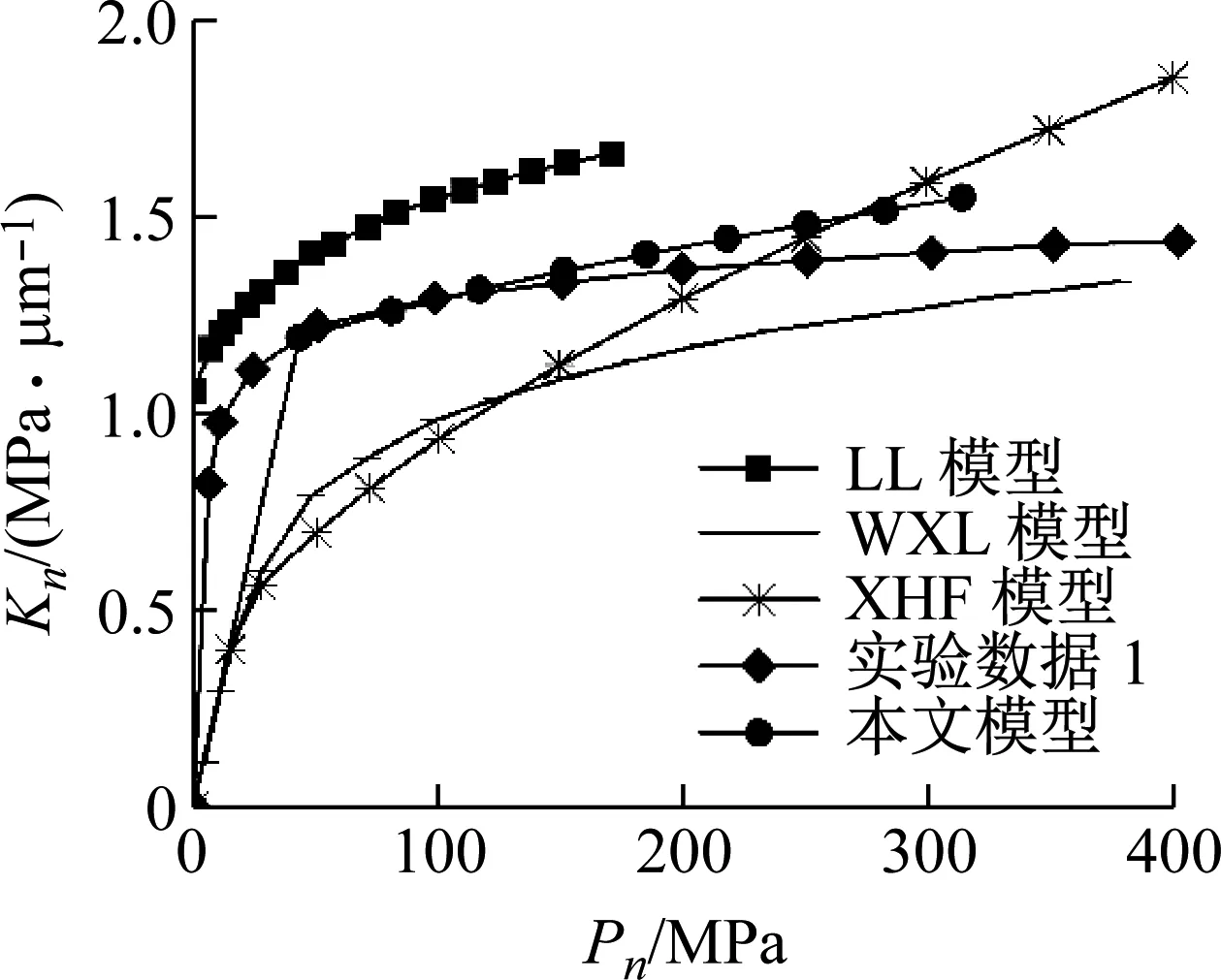
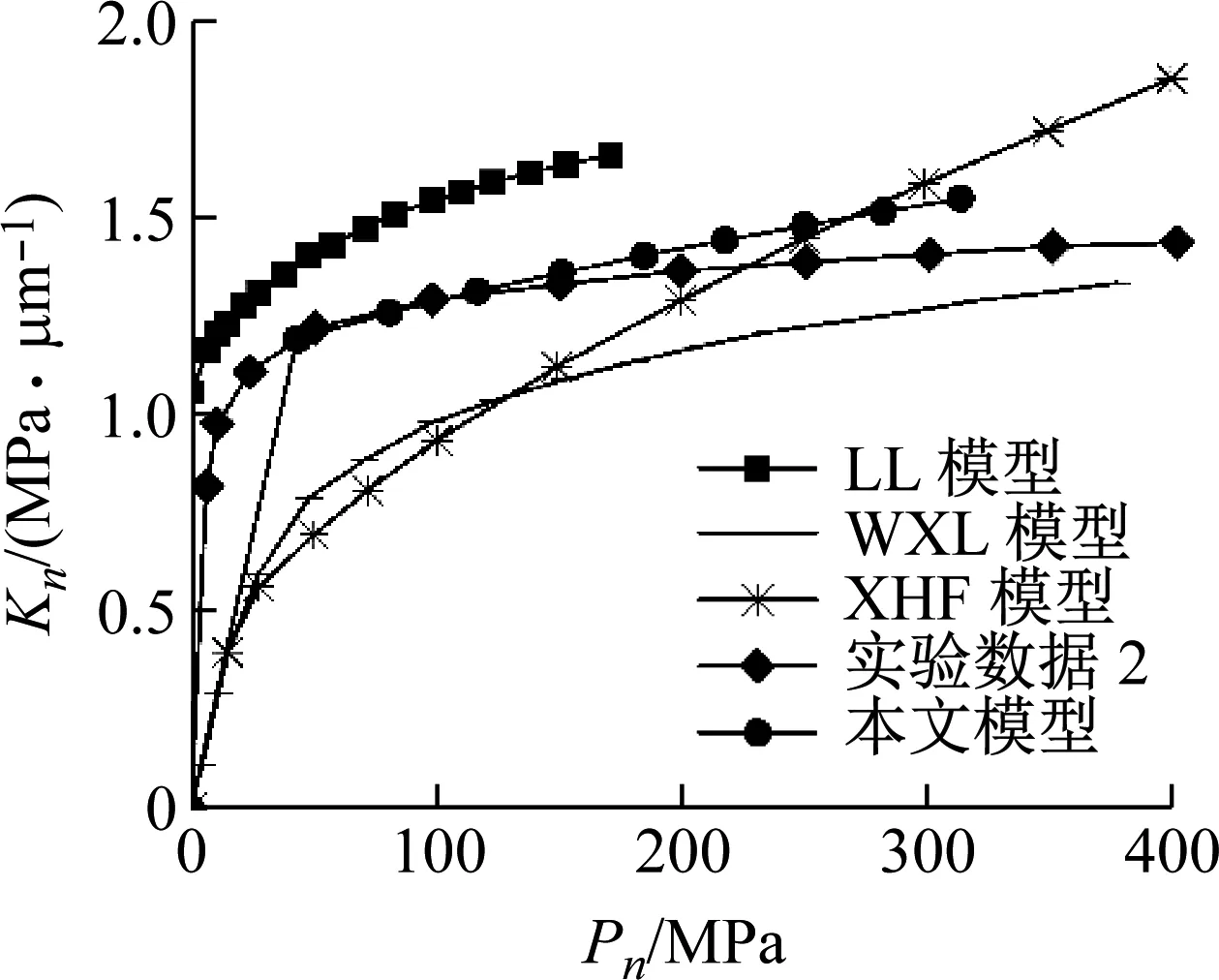
式中:z(x,y)为指粗糙表面微观形貌随机轮廓高度;L为取样长度;D为分形维数,且取值范围为2 粗糙表面的三维表面与二维轮廓如图1所示。其中仿真参数为:L=0.61 μm,M=10,γ=1.5,D=2.4、2.8,G=1.36×10-8。 (a) G=1.36×10-8,D=2.4 从图1可看出,粗糙表面的三维表面和二维轮廓都与分形维数有着重要的关系。当粗糙表面的分形粗糙度恒定时,分形维数越大,粗糙表面间的波峰与波谷的差值越小,表面粗糙度愈小,粗糙表面愈加光滑,即分形维数D表述了粗糙表面的表面粗糙度。 在实际接触过程中,结合面间总会存在润滑油,润滑油在结合面间形成一层油膜,因此结合面间既存在微凸体与微凸体接触又存在油膜与微凸体接触,将结合面接触等效后,就会形成微凸体-刚性平面接触和油膜-刚性平面接触,此时,结合面的法向载荷由等效微凸体和润滑油膜共同承担。混合润滑结合面的接触示意图如图2所示。 图2 混合润滑状态下结合面接触等效模型Fig.2 Normal contact equivalent model of joint surface under mixed lubrication 将两粗糙表面接触等效为刚性平面和粗糙表面接触,润滑油充满粗糙表面与刚性表面的间隙,形成固体-固体接触表面和固体-液体接触表面,由混合润滑结合面的法向载荷分配[12]得,结合面外部法向载荷由润滑油膜压力和微凸体接触力共同承担,结合面接触刚度K等效为固体接触刚度KS与液体油膜接触刚度KL的并联连接模型,则结合面的接触总刚度K为微凸体接触刚度和液体润滑油膜接触刚度之和,即: K=KS+KL (2) 式中:KS为固体接触刚度;KL为液体接触刚度;等效后粗糙表面的均面与刚性平面之间的距离为h。从图2可看出,当h增大时,微凸体接触面积减小,液体接触面积增大,液体接触刚度在结合面的接触总刚度中占比增加;当h减小时,微凸体接触面积增大,液体接触面积减小,固体接触刚度在结合面的接触总刚度中占比增加。 两粗糙表面相互接触时,一般等效为刚性平面与粗糙表面的接触,粗糙表面上的微凸体变形部分一般等效为球形,球形等效时以余弦波为曲率半径,但微凸体的真实体积小于等效球体的体积[13],因此圆锥微凸体更接近实际接触[14]。为了减小等效微凸体的体积,本文采用与等效球形类似的方法,以余弦波的顶点和余弦波与刚性平面接触的两点为端点建立等腰三角形,并作为正视图,将微凸体变形部分等效为圆锥模型,如图3所示。 图3 微凸体等效模型Fig.3 Micro-convex equivalent model 由图3可知,δ为微凸体的变形量;β为圆锥微凸体的半顶角;r为等效微凸体的截面半径;则微凸体的实际接触面积为:a=πr2。 由文献[15],单个微凸体的波峰与波谷的高度差即为单个微凸体的变形量δ,则变形量δ为 (3) 从图3中可看出,半顶角β的余切值为 (4) 由文献[16],单个圆锥微凸体在弹性阶段所受应力为 σc=0.2Ecot(β) (5) 则单个圆锥微凸体在弹性变形阶段所受法向载荷与接触面积的关系为 Pe=σca=0.2Ecot(β)a (6) 其中,E为两接触粗糙表面的综合弹性模量,且E为: (7) 式中:E1和E2分别为两接触粗糙表面的弹性模量;v和v2分别为两接触粗糙表面的泊松比。 单个圆锥微凸体在弹性变形阶段所受法向载荷与分形维数D和分形粗糙度G结合得 (8) 由式(4)可得,在弹性变形阶段,单个圆锥微凸体所受的平均载荷为 (9) 因刚度是材料或结构抵抗受力时弹性变形的能力,因此可得单个圆锥微凸体的法向接触刚度为 (10) 结合式(3)、式(7)和式(9)化简得 (11) 在塑性变形阶段,单个圆锥微凸体所受法向载荷为 Pp=Ha (12) 式中,H为较软材料的硬度 由式(12)可得,在塑性变形阶段,单个圆锥微凸体所受的平均载荷为 (13) 假设圆锥微凸体由弹性变形进入到塑性变形时连续,则圆锥微凸体在临界变形处所受的平均载荷也连续,即: Pea=Ppa (14) 则单个圆锥微凸体由弹性变形转变为塑性变形时的临界接触面积为 (15) 式中:σy为较软材料的屈服强度,k=H/σy;φ为塑性指数,φ=σy/E。 粗糙表面接触面积分布函数表达式[17]为 (16) 式中,al为结合面间所有微凸体中的最大接触面积。 则结合面间的实际接触面积为 (17) 粗糙表面的法向总载荷为 (18) 把式(6)、式(12)、式(16)代入到式(18)得 (19) 结合面的法向总刚度为 (20) 把式(10)和式(15)代入式(19)得 (21) 将式(19)和式(21)进行无量纲化得 (22) (23) 混合润滑状态下存在粗糙表面-润滑介质-粗糙表面的接触模型,润滑介质在两个粗糙表面之间形成一层油膜,将两粗糙表面等效为刚性平面,两刚性平面之间为润滑油膜,油膜厚度h为两等效刚性平面之间的距离,等效液体刚度接触模型见图2。 由于刚性平面与润滑油膜的声阻抗有着明显的差异,当入射超声波通过刚性平面与油膜时,超声波发生反射与透射,因此可以测量刚性平面与润滑油膜的声阻抗以及反射系数;而反射系数与润滑油膜的厚度和刚度之间有着确定的关系,以此来计算润滑油膜的刚度。 根据固体-液体接触界面油膜共振模型可得,固体-液体接触界面的超声波反射系数为[18] (24) 式中:λ0为超声波在润滑油膜中的波长;Z1为刚性平面的声阻抗,Z1=ρ1c1,ρ1为刚性平面的密度,c1为超声波在刚性平面中的波速;Z2为润滑油膜的声阻抗,Z2=ρ2c2,ρ2为刚性平面的密度,c2为超声波在刚性平面中的波速。本文中计算具体取值应用文献[19]的数据,如表1所示。 表1 固体和不同润滑介质的声学特性Tab.1 Sound parameters of solid and different lubricants 根据润滑油膜的等效弹簧模型,当润滑油膜厚度h与超声波在润滑油膜中的波长λ0相比相差较大时,可把润滑油膜看作是一个反射超声波的整体,则固体-液体接触界面的超声波反射系数[20]可表示为 (25) 式中:k1为单位面积上润滑油膜的接触刚度;f为超声波的频率。 联立式(24)和式(25),单位面积上润滑油膜的接触刚度为 (26) 因超声波在润滑油膜中的波长λ0远大于润滑油膜的厚度,因此可假设 (27) (28) 将单位面积上润滑油膜的接触刚度拓展到整个接触面,即考虑名义接触面积,则润滑油膜接触刚度为 (29) 对式(29)无量纲化得 (30) 联立式(23)和式(30)可得,混合润滑下粗糙表面的法向接触总刚度为 (31) 式(31)表明,混合润滑下粗糙表面的法向接触刚度与分形维数、接触表面的粗糙度、微凸体高度标准差、润滑油膜厚度和润滑介质等因素有关。 (a) (a) D=2.1 综合分析为: (1) 当粗糙表面的实际接触面积为恒定值,分形维数渐增但不大于2.6时,结合面间相互接触的微凸体数量增多,圆锥微凸体接触面积增大,处于弹性变形状态的圆锥微凸体总数占比减小,同时处于塑性变形状态的总数占比增大,固体接触刚度增大;同时,实际接触面积为恒定值,因微凸体接触面积增大而使液体接触面积减小,则液体法向接触刚度略微减小,此时前者起主导作用,因此法向接触总刚度呈现上升趋势; (2) 实际接触面积为恒定值,当分形维数渐增且大于2.6时,结合面中微凸体的高度差减小,两等效表面间的距离减小,结合面间润滑油膜接触面积增大,相互接触的圆锥微凸体数量减少,致使圆锥微凸体接触面积减小,则结合面中固体法向接触刚度下降明显;同时,润滑油膜接触面积增大,油膜厚度减小,微凸体高度标准差也减小,因此液体接触刚度增大,此时结合面间的法向接触刚度主要由润滑油膜承担,因固体法向接触刚度减小幅度明显,因此法向接触总刚度呈现下降趋势。 (3) 实际接触面积为恒定值,当分形粗糙度渐增,结合面宏观表面越粗糙,微观下结合面中的微凸体高度差增大,相互接触的圆锥微凸体数量减少,圆锥微凸体接触面积减小,处于弹性变形状态的圆锥微凸体总数占比减少,处于塑性变形状态的总数占比增大,因微凸体接触面积减小幅度较大,此条件占主导地位,因此固体接触刚度降低;因微凸体接触面积减小,则润滑油膜接触面积增大,微凸体高度差增大,两等效平面间的距离增大,润滑油膜厚度增大,润滑油膜所承担载荷减小,致使液体接触刚度减小,因此,随着分形粗糙度的渐增,结合面法向接触总刚度逐渐降低,且分形维数越大,下降趋势越明显。 (a) D=2.2 文献[8]中设计了一组试验用来测算混合润滑结合面间的力学特性,试验简图如图7所示,该试验是利用超声波测量仪和电子探针来探测加入润滑液之后结合面间的接触刚度特性。其工作原理是:超声波脉冲接收器(UPR)用于产生电压脉冲,以驱动压电换能器,传感器(此情况下为10 MHz纵波)连接到UPR,该电压会产生一个宽频带的短时超声波脉冲,该脉冲从接口反射回来,并由同一传感器接收,需要记录的电压随后被UPR捕获,并作为波形存储在数字示波器上。 图7 文献[8]试验原理图Fig.7 Experimental schematic diagram of reference [8] 文献[8]中采用的接触表面的粗糙度如表2所示,依据表2中的参数分别记为试验数据1和试验数据2;文献[10]中的模型是基于统计学计算方法建立的模型,记为XHF模型;然后与本文模型和试验数据进行对比验证,验证结果如图8和图9所示。 表2 接触表面的分形粗糙度值Tab.2 Fractal roughness of contact surface 图8 不同模型与试验数据1对比Fig.8 Comparison of different models with experimental data 1 图9 不同模型与试验数据2对比Fig.9 Comparison of different models with experimental data 2 从图8和图9中可看出,不同润滑介质下,本文模型预测刚度与试验测量数据基本一致,验证了本文模型的正确性;与XHF模型、WXL模型和LL模型相比,本文模型进一步提高准确度。混合润滑结合面的接触刚度与接触表面的平滑程度、油膜厚度以及润滑剂有关。结合面的平滑程度是由粗糙表面的加工方法决定的,加工方法也间接决定了油膜厚度,因此选择合适的加工方法有助于改善混合润滑结合面的接触特性。本文模型的预测值偏离试验值的主要原因在于:微凸体接触时的变形阶段分为弹性变形、弹塑性变形和塑性变形三种变形阶段,而本文只考虑了弹性变形阶段和塑性变形阶段;本文模型还忽略了微凸体在接触时产生的摩擦和微凸体的相互作用。 (1) 本文将结合面微凸体等效为圆锥微凸体,并基于分形理论、改进的W-M函数和油膜共振模型,建立了混合润滑状态下结合面法向接触刚度三维分形模型。 (2) 结合面无量纲法向接触总刚度随着分形维数的增大呈现出先增大后减小的趋势,且在分形维数为2.6附近时取得最大值;随着无量纲法向载荷的增大和无量纲分形粗糙度的减小而增大。 (3) 混合润滑状态下结合面无量纲法向接触总刚度高于无润滑介质结合面无量纲法向接触刚度,且液体接触刚度受润滑介质影响较大。 (4) 将本文模型和其他模型与试验数据进行对比,本文模型的预测值与试验数据拟合度较好,验证了本文模型的准确性,可用于混合润滑状态下结合面的接触特性的分析与预测。
2 混合润滑结合面的法向接触刚度等效模型

3 圆锥微凸体接触等效模型
3.1 粗糙表面的三维分形模型

3.2 结合面接触模型
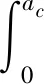
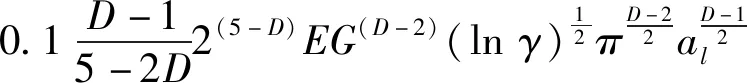




4 液体接触刚度模型


5 混合润滑下粗糙表面接触法向总刚度

6 仿真计算与结果分析
6.1 分形参数和法向接触总刚度的关系
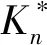


6.2 不同润滑介质和法向总刚度的关系
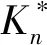

7 试验验证


8 结 论

