一种应用于射流破岩的孔隙形状近似法

马小晶,周新超,肖新朋,程 璨

(新疆大学 电气工程学院,乌鲁木齐 830017)

随着常规油气资源的减少以及能源需求的增长,石油天然气的开发逐渐从常规油气资源转移到了非常规油气资源[1]。由于我国蕴藏着较丰富的砂岩致密油(发展致密油的开采技术是十分必要的,且致密油的存储规律和存储形态与岩体内部的孔隙结构及孔隙间的相互连通性有着密切的关系[2],因此,需要对含有孔隙结构的岩体在常规作业中产生的影响展开深入研究[3]。

高压水射流能够大面积且有导向的碎裂储层岩体,方便致密油等油气资源的解吸与渗流,已被广泛应用于钻井开采领域[4]。众多学者采用不同的数值模拟方法研究了各类射流破岩问题[5],但针对射流冲击含孔隙岩体的破损过程以及孔隙结构对破岩效果的研究相对较少。为了深入探究含孔隙岩体的破损机制,需要构建能够真实反映岩体中复杂孔隙结构和分布的模型,为进一步提高岩体破损问题的模拟精度提供途径。

目前,国内外学者已对孔隙结构的模型构建技术及相关问题展开了大量研究。隋微波等[6]将真实的孔隙抽象简化为椭球和球体,研究了三维抽象孔隙模型中孔隙结构特征对孔隙体积压缩系数的影响;蔡少斌等[7]为探究油气资源在岩石多孔介质内部的迁移过程,建立了孔隙空间模型,并对多相流体的运动进行了模拟研究;李俊键等[8]提取了孔隙网络结构模型,分析了微观孔喉结构的非均质性对剩余油分布形态的影响。为了构建更加接近真实岩体结构的数值模型,李博等[9]采用数字岩心技术(digital core technology,DCT)生成了含裂隙的岩体三维微观结构模型,计算了不同孔隙度下基质的介电性质。数字岩心技术能够生成非常接近真实岩体的微观孔隙结构,但需要具体的岩心样本且生成步骤较复杂,并存在计算困难等问题[10]。

本文基于光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法,提出一种孔隙形状近似(pore shape approximation,PSA)法,建立了含孔隙结构岩体的数值模型,通过模拟孔隙岩体的单轴压缩试验,验证了该孔隙结构生成方法的有效性;在此基础上,引入描述射流和岩体力学特性的NULL型和H-J-C型本构关系,构建出射流冲击岩体的动力学模型,并将模拟结果与试验结果进行对比分析;之后模拟研究了射流冲击含孔隙结构岩体的动态过程,并将孔隙形状近似法与数字岩心技术生成岩体模型的破损过程进行了对比分析;最后着重研究了含不同的孔隙形状、孔隙尺寸及各种形状孔隙占比的岩体在射流冲蚀下的破损规律。

1 SPH方法的基本理论

SPH方法作为一种纯拉格朗日的无网格粒子法,是将计算域离散为一系列可运动的粒子,粒子的物理属性可以通过求解非稳态N-S控制方程得到,适用于模拟冲击作用下的大变形和破损现象。粒子的场函数可通过周围粒子的函数进行加权近似求解,即[11]

(1)

式中:f(x)为坐标向量x的函数;Ω为x的支持域;x-x′为粒子间距离;h为光滑长度;W是核函数,即:

(2)

式中,d为空间维数。用粒子近似法将连续形式积分方程写为离散形式的方程,即:

(3)

式中:ρi和mi分别为粒子i的密度和质量。

2 岩体内孔隙模型的构建方法

2.1 孔隙形状近似法

孔隙的形状、尺寸以及连通性等会直接影响开采效率,但岩体内部的孔隙结构十分复杂,数值建模时常会尽可能的简化孔隙结构。Silin等[12]将岩体中的孔隙和孔隙连通喉道分别近似为球体和棍状,建立了微观孔隙结构的数值模型;Sadowsky等[13-14]将孔隙形状视为圆柱体和狭长裂缝等,建模时均抽象为椭球体。

为了构建更加贴近真实的岩体内部孔隙结构的模型,本文扫描了4块砂岩样本,采用的CT型号为 phoenix v|tome| x m,扫描精度的分辨率为30 μm,岩石样本的直径为30 mm,高度50 mm。每块样本得到175张图片,通过处理和分析上述图片研究了砂岩内部的孔隙形状。图1给出了砂岩样本和孔隙近似形状的示意图,砂岩内部的孔隙形状及分布都较为复杂,不可能只存在某单一形状的孔隙,鉴于此,本文提出一种基于SPH方法的孔隙形状近似法,在前人将孔隙简化为球体和椭球体的基础上,结合扫描图增加了其他三种近似形状,即:薄片体、正三棱柱和正三棱锥,并将孔隙喉道近似为棍状。

(a) 砂岩样本

2.2 离散孔隙的构建原理

由于研究采用了适用于模拟大变形和破损现象的SPH方法,因此本文将射流、岩体及其内部的孔隙结构均离散为一系列的粒子,图2给出了不同形状的孔隙的模型示意图,图中θ代表孔隙尺寸的指标。

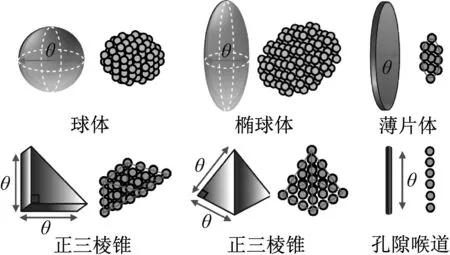
图2 不同形状的孔隙模型示意图Fig.2 Model of pores with different shapes

研究中采用了蒙特卡洛法随机生成孔隙[15],孔隙均匀分布在岩体内部,并且允许孔隙之间存在部分重叠,同时在孔隙之间还构造了多条起连通作用的孔隙喉道,使构建的孔隙结构更加接近天然岩体的形成过程。图3给出了几种形状的孔隙及孔隙喉道在岩体内部的分布方向。

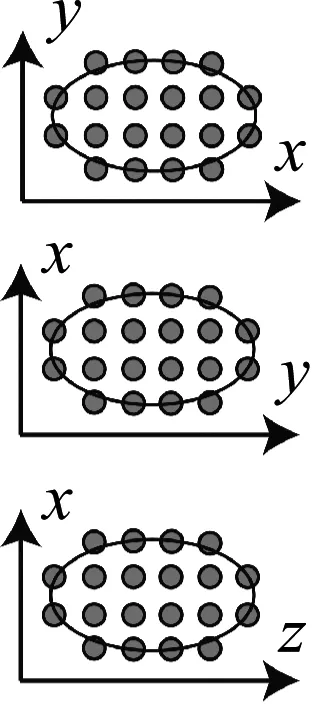
(a) 薄片体和椭球体

LS-DYNA软件中生成岩体模型的步骤为:

步骤1沿X轴排布一列粒子,改变Z轴位移,继续沿X轴排布粒子,如此反复,最终构成一个粒子面;

步骤2改变Y轴位移,按步骤1沿Y轴生成一面粒子,重复上述过程,最终生成一个由SPH粒子构成的三维岩体,存储在K文件中。

本研究通过K文件获得岩体模型中粒子的坐标位置,提取部分岩体粒子并替换为孔隙粒子,即可生成不同形状的孔隙,构建出含孔隙结构的岩体模型。以正方体孔隙为例,生成过程如图4所示,步骤为:

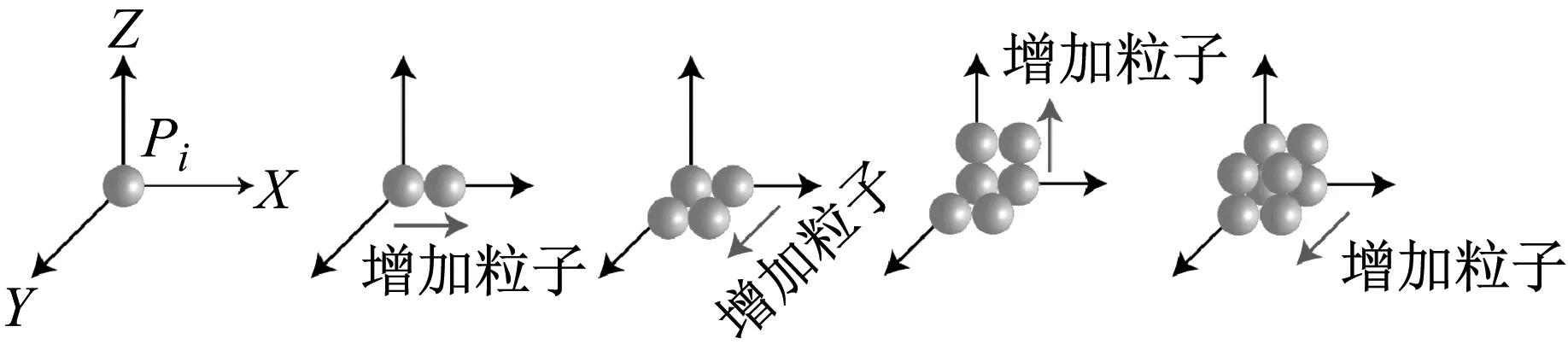
图4 生成正方体孔隙的示意图Fig.4 Schematic diagram of generating cube pores

步骤1使用随机函数抽取岩体粒子的坐标位置,确定出生成孔隙的基准粒子Pi的坐标信息;

步骤2按照粒子的间隔距离,在基准粒子的位置上分别沿X轴、Y轴和Z轴三个方向增加2个粒子,确定出构成正方体结构的8个粒子坐标,之后将这8个粒子的属性替换为孔隙粒子,从而形成正方体孔隙;

步骤3采用随机函数抽取粒子位置,重复上述步骤1和2不断生成孔隙,直到孔隙个数达到要求。

2.3 孔隙形状近似法的验证

为了验证本文提出的孔隙形状近似法的有效性,采用SPH方法和文献[16]的砂岩的单轴压缩试验数据对该试验进行了模拟,模型尺寸3 mm×3 mm×3 mm的正方体,孔隙特性等参数参见文献[16],岩体上表面施加位移荷载,底面建立刚体网格并施加固定约束。图5为孔隙岩体Von-Mises应力分布云图,由图5可知,由于岩体内部有孔隙结构,岩石内部的Von-Mises应力分布并不均匀,并且在孔隙附近存在应力集中现象,这与文献[16]中采用网格法得到的模拟结论一致。

文献模型[16](t=0.2 ms)

图6为经过数值计算得到的孔隙岩体的应力应变曲线,与文献[16]中的参考模型拟合曲线相比,本文在前期的上升趋势保持一致,并且差距较小。根据该曲线可得出本文孔隙岩体模型的整体弹性模量为31.987 GPa。表1给出了孔隙岩体的整体弹性模量,由表1可知,文献[16]采用数字岩心方法和本文提出的孔隙形状近似法构建的孔隙岩体模型的弹性模量均小于无孔隙砂岩的弹性模量,这说明岩体内部的孔隙结构在一定程度上会影响其力学特性,与文献[17]的研究结论吻合。因此,为了分析更加接近实际的射流破岩动态过程,本文在岩体中引入孔隙结构。与文献[16]中数字岩心方法构建的孔隙岩体模型相比,本研究的整体弹性模量更加接近实际值,这表明基于孔隙形状近似法建立的孔隙岩体模型更符合实际,应用于数值模拟可获得更加精确的研究结果。

表1 孔隙岩体的整体弹性模量Tab.1 Overall elastic modulus of porous rock

图6 孔隙岩体的应力应变曲线Fig.6 Stress-strain curve of porous rock

3 孔隙形状近似法在射流破岩的应用

3.1 岩体和射流的本构关系

本文构建了基于SPH方法的水射流破岩模型,水射流采用NULL本构关系进行描述,并赋予Gruneisen状态方程[18],即:

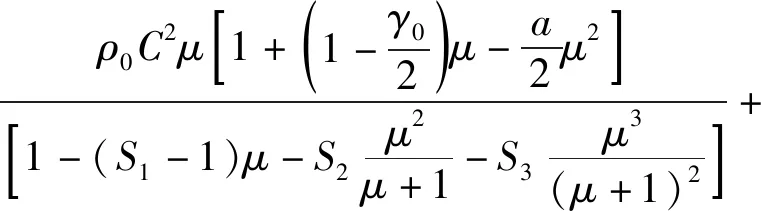
(γ0+aμ)Ea

(4)

式中:C为冲击波速度与质点速度变化曲线截距;S1、S2、S3为冲击波与质点速度变化曲线的斜率系数;γ0为Gruneisen常数;a为一阶体积修正量。具体参数如表2所示[19]。

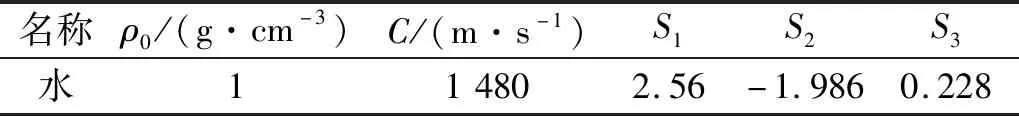
表2 水射流的参数Tab.2 Parameters of water jet

研究选用了存储致密油的砂岩,材料参数如表3所示[20],满足H-J-C本构关系,屈服面方程为[21]

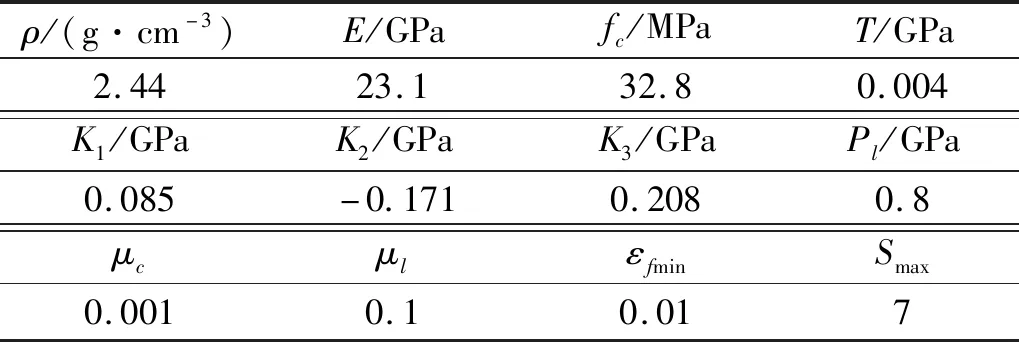
表3 砂岩的参数Tab.3 Parameters of sandstone

σ*=[A(1-D)+Bp*N](1-Clnε*)

(5)

式中:σ*为岩体冲击载荷下等效应力与静态屈服强度之比;P*为岩体实际压力与静态屈服强度之比;ε*为冲击载荷下岩体应变率与静态应变率之比;A、B、N和C为材料的强度参数,D为损伤因子。

3.2 射流冲击含孔隙岩体的SPH模型

针对研究的射流冲击含孔隙岩体问题,本文采用LS-DYNA软件进行分析。模型简化为水射流、含孔隙结构的岩体和孔隙物质三种物质,暂不考虑气相环境的影响。研究采用了1/2对称模型,对称面施加SPH_SYMMETRY_PLANE约束,并对岩石周围与底面施加SPH_NON_REFLECTING约束模拟岩体的无限大边界,同时约束岩石的竖向移动。对称后的岩体为10 mm×5 mm×5 mm的长方体,射流直径为1 mm,长度为5 mm。模型共由691 460个粒子构成,其中5 460个为射流粒子,孔隙及孔隙喉道内部填充水,其本构关系和材料参数与水相同。图7为射流冲击孔隙岩体的模型示意图。

图7 射流冲击孔隙岩体的模型示意图Fig.7 Model of jet impacting porous rock

3.3 模型的验证与分析

(1) 射流破岩问题

为了验证本文建立的射流冲击岩体模型的有效性,对Xue等[22]研究的水射流冲击无孔隙煤岩问题进行了模拟,各项参数均与文献设置保持一致,岩体部分的模型是半径25 mm,高度50 mm的圆柱体,射流直径为1 mm,长度为50 mm。

图8和图9分别给出了t=0.06 ms时煤岩的破损坑形状与破损坑深度随冲击时间的变化曲线。从图8可以看出,本模型的破损坑深度、形状与文献[22]的模拟结果基本相同,符合试验结果的冲孔形态。由图9可知,随着冲击时间的增加,煤岩的破损坑深度不断增大,与文献[22]的模拟结果基本一致,验证了本文建立的射流破岩模型的有效性。

本文模拟结果(t=0.06 ms)

图9 煤岩破损坑深度随时间的变化曲线Fig.9 Variation curve of coal rock damage pit depth with time

(2) 孔隙形状近似法与数字岩心技术的对比

在上节所构建的水射流冲击无孔隙岩体模型的基础上,采用孔隙形状近似法建立了含孔隙岩体的数值模型,模拟研究水射流冲击破岩的动态过程,并与数字岩心技术的模拟结果进行了对比分析。

图10为模型的构建流程,DCT是对砂岩的CT扫描图片进行处理,通过Avizo等软件提取孔隙结构,而PSA模型则只需根据扫描得到的孔隙度和孔隙尺寸等核心特性参数即可生成孔隙结构。DCT所构建的岩体模型数据来源于Berea砂岩,孔隙度为14.9%,本文采用PSA构建出孔隙度和孔隙平均尺寸与其相同的岩体模型,两种模型都采用了1/2对称模型,岩体尺寸为10 mm×5 mm×5 mm的长方体,射流直径为1 mm,长度为5 mm。

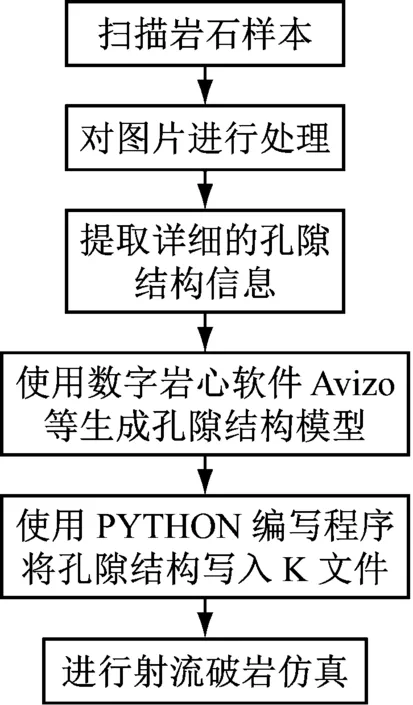
(a) DCT

图11为上述两种方法所构建的孔隙岩体模型在水射流冲击作用下的破损演化过程,图中蓝色、绿色和红色分别为水、孔隙和岩体。由图11可以看出,在射流的持续冲击作用下,两种岩体模型的破损坑均逐渐增大,破损形状的变化过程基本一致。

(a) DCT

本文选取了破损坑横截面的破损宽度指标w和破损坑纵截面的破损深度指标h以及破损面积指标s来反映岩体的破损情况,其中S是初始岩体纵截面的面积,s为该截面破损坑的面积,如图12所示。

图12 岩体破损指标的示意图Fig.12 Diagram of rock damage index

图13给出了数字岩心模型和孔隙形状近似法模型的破损指标随冲击时间的变化规律。

(a) 破损宽度

由图13可知,上述两种模型的破损宽度除在t=0.012 ms和t=0.02 ms时存在较小差异外,其他冲击时间的变化趋势基本相同;两种模型的破损面积的变化曲线则几乎完全重合。由此可知,采用DCT和PSA所建的岩体模型可得到较为一致的破损规律,这说明本文所提的孔隙形状近似法应用于射流破岩问题是可行的。

表4给出了孔隙形状近似法和数字岩心技术所建模型的计算总时间。两者的模型参数完全一致,冲击总时长为0.021 ms,分别选取3种不同孔隙平均尺寸进行对比,数值计算处理器为英特尔i5-10400F。由表4可知,在相同的孔隙平均尺寸下,采用数字岩心技术生成的孔隙岩体模型的模拟耗时大于孔隙形状近似法,尤其是孔隙平均尺寸较大时,数字岩心技术构建的模型还会出现计算崩溃的现象。显然,本文提出的孔隙形状近似法构建的模型计算效率高且稳定性好。

表4 不同模型计算时间Tab.4 Calculation time of different models

4 孔隙对岩体破损影响的研究

将孔隙形状近似法应用于射流破岩的模拟研究中,分析含不同的孔隙尺寸、孔隙形状以及各形状孔隙占比的岩体在射流冲蚀下的破损规律。岩体模型的参数均取尺寸为10 mm×5 mm×5 mm,孔隙度为21%(19%为孔隙,2%为孔隙喉道),射流速度为500 m/s,冲击总时间为0.21 ms,取破损面积为岩体破损指标。

4.1 孔隙的尺寸和形状

为了分析孔隙尺寸和形状对射流作用下岩体破损规律的影响,本文对内部仅含单一形状孔隙和孔隙喉道的岩体的射流破损过程进行了模拟研究。通过研究4块砂岩样本的实际孔隙结构,确定了岩体模型中各个形状孔隙尺寸指标θ(参见本文2.2节的图2)的范围,球体和椭球体孔隙的θ取值分别为0.214 mm、0.285 mm,0.357 mm、0.428 mm、0.5 mm、0.571 mm、0.642 mm和0.714 mm,薄片体、正三棱柱和正三棱锥的θ取值分别为0.142 mm、0.285 mm,0.357 mm、0.428 mm、0.5 mm、0.571 mm和0.642 mm,其中椭球体和薄片体的纵横比定义为长轴/短轴,纵横比的取值范围1.3～2.2。

不同的孔隙形状和尺寸会直接影响岩体的破损程度,图14给出了t=0.021 ms时含不同孔隙形状和尺寸岩体的破损情况。由图14可知,由于孔隙在岩体内部随机分布,岩体会呈现出不同破损形状,孔隙分布较多的岩体区域在射流作用下更容易破损。从图14还可知,当0.142 mm<θ<0.375 mm时,在相同的孔隙尺寸下,孔隙形状对岩体破损程度的影响较为接近;当θ>0.375 mm时,孔隙形状为薄片体、正三棱柱的岩体破损程度大于球体、椭球体的岩体。

图15给出t=0.021 ms时不同尺寸孔隙的破损指标对比。由图15(a)可知,当θ<0.571 mm时,薄片体孔隙的破损宽度最大,且在θ=0.375 mm时达到最大值。从图15(b)可知,当θ=0.428 mm时,含椭球体、薄片体和正三棱柱孔隙岩体的破损深度较大,其中薄片体孔隙岩体的破损深度最大;当θ=0.5 mm和0.571 mm时,含薄片体、正三棱柱和正三棱锥的孔隙岩体破损深度较大。由图15(c)可知,当0.142 mm<θ<0.375 mm时,在相同孔隙尺寸下,孔隙形状对岩体破损面积的影响较为接近;当θ>0.375 mm时,含薄片体、正三棱柱的孔隙岩体的破损面积大于球体、椭球体的岩体;当θ=0.571 mm时,正三棱锥的孔隙岩体破损面积最大。

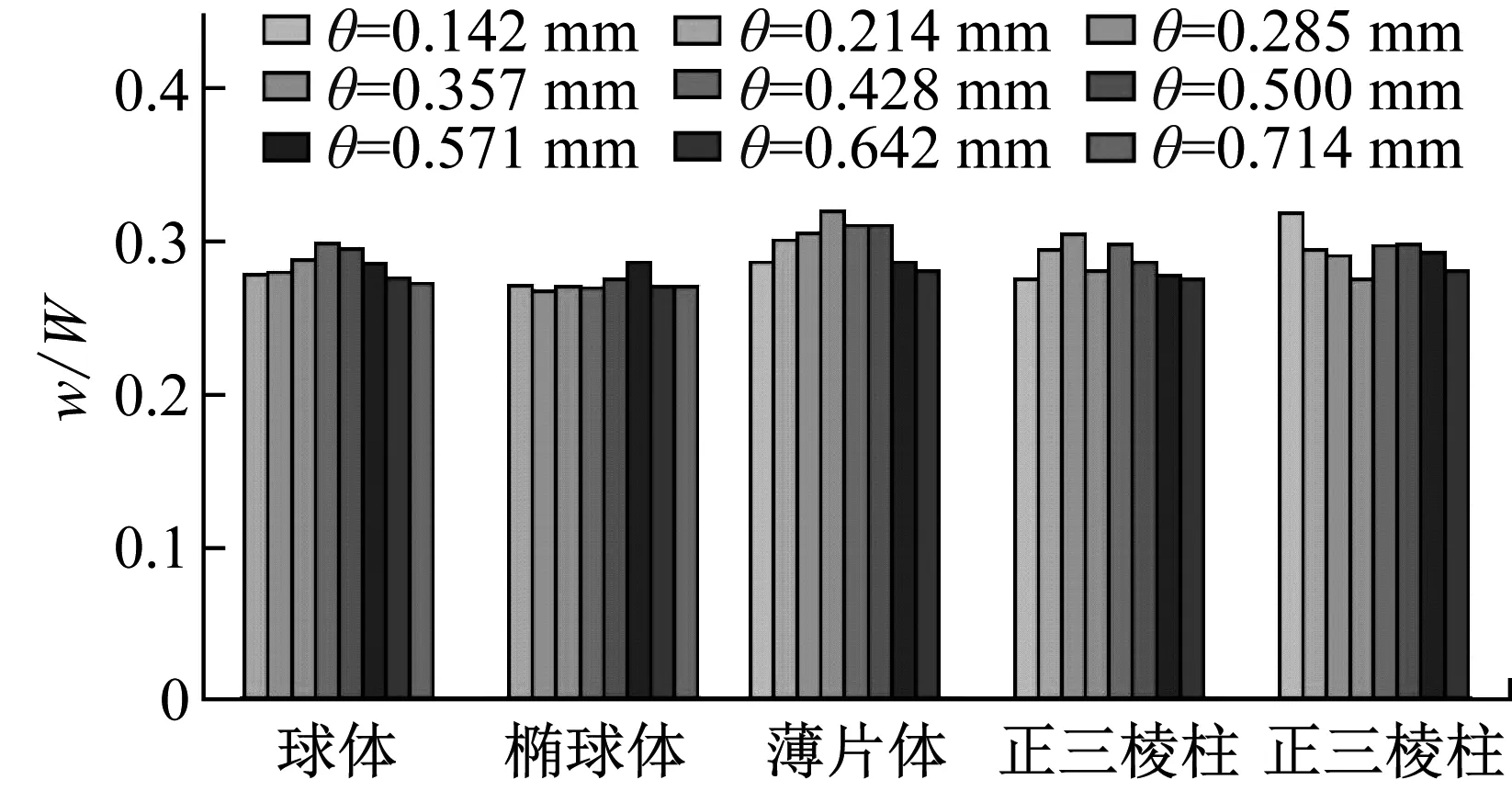
(a) 破损宽度

综上,薄片体孔隙在特定的尺寸下,破损宽度、破损深度和破损面积远大于其他形状的孔隙;当孔隙尺寸较大时,孔隙形状为薄片体、正三棱柱和正三棱锥的岩体在射流冲击作用下更容易破损,不同形状的孔隙都存在使岩体破损面积达到最大的孔隙尺寸。

4.2 不同形状的孔隙在岩体中的占比

本文分析了不同形状孔隙占比对射流破岩效果的影响,构建了6种孔隙岩体模型,孔隙平均尺寸保持一致。岩体模型A、B、C和D是基于4块砂岩样本的孔隙特性进行构建,岩体模型E和F则根据文献[6]中Berea砂岩和Bentheimer砂岩进行构建,孔隙形状占比如表5所示。

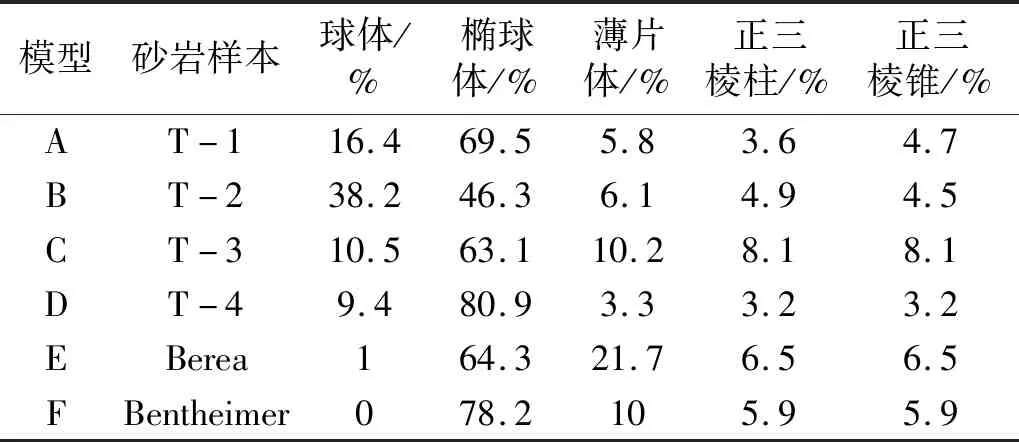
表5 模型中的孔隙形状占比Tab.5 Proportion of pore shape in the model

图16为t=0.021 ms时不同岩体模型在射流冲击作用下的破损效果。由图16可知,不同岩体模型的破损坑形状有明显的差异。图17给出了不同模型岩体的破损面积随冲击时间的变化曲线。由图可知,模型C和E以及F的破损面积大于其他模型,其中模型E的破损面积最大,结合表5可以发现,岩体模型C、E和F中薄片体、正三棱柱和正三棱锥孔隙占比相对较高,说明这类形状孔隙的存在会使岩体更容易发生破损。

图16 不同岩体模型的破损效果(t=0.021 ms)Fig.16 Damage effect of different models (t=0.021 ms)

图17 不同模型下破损面积随冲击时间的变化曲线Fig.17 Variation curve of damage area with impact time under different models

5 结 论

(1) 针对岩体内部的孔隙结构,提出一种用于SPH方法的孔隙形状近似法,构建了孔隙岩体的数值模型,通过模拟岩体的单轴压缩试验,验证了含孔隙结构岩体模型的有效性。

(2) 将孔隙近似法应用于基于SPH方法的射流破岩模拟研究中,并与数字岩心技术的模拟结果进行了对比分析,结果表明数字岩心技术和孔隙形状近似法构造的孔隙岩体模型具有相同的破损规律,并且孔隙形状近似法具有较好的稳定性和效率。

(3) 模拟研究了孔隙形状、孔隙尺寸和不同形状孔隙的占比对射流破岩的影响,研究结果表明,不同形状的孔隙均存在一个使岩体破损最严重的孔隙尺寸;孔隙为薄片体、正三棱柱和正三棱锥,且孔隙的占比较高时,岩体则更容易被射流破损。针对目前在射流破岩领域中对含孔隙岩体的研究较少的情况,提出了一种应用于射流破岩领域的孔隙形状近似法。