外包型钢加固箍筋锈蚀混凝土柱恢复力模型研究
李 强,董嘉辉,常迪文,金宇琨
(1.西安科技大学 建筑与土木工程学院,西安 710000;2.西安科技大学 建筑结构检测与加固研究所,西安 710000)
钢筋混凝土结构已经成为当今世界上工程用量最大,建筑用途最广的结构。随着混凝土结构在工作环境中服役时间的增长,结构所面临的钢筋锈蚀等耐久性问题日益严重[1]。由于箍筋位于混凝土外侧,锈蚀首当其冲。为保证锈蚀结构的安全使用,必须对其进行抗震加固,提高锈蚀结构的抗震性能[2-3]。随着地震发生,建筑结构损伤不断加剧,恢复力模型作为描述结构在反复荷载作用下本构关系的依据就显得尤为重要,开展相关研究也变的必不可少[4-6]。
目前,国内外学者已经在主筋锈蚀混凝土柱和加固混凝土柱的恢复力模型方面开展了初步的研究。张猛等[7]在建立恢复力模型时考虑了主筋锈蚀率和轴压比等因素的影响。梁岩等[8-9]综合考虑了钢筋锈蚀后引起的钢筋和混凝土力学性能的变化、截面损伤、锈蚀钢筋混凝土黏结滑移能力降低等因素建立了恢复力模型。牛荻涛等[10-12]以退化三线型(D-TRI)模型为基础,给出了适合主筋锈蚀构件的恢复力模型中关键点的计算方法,同时给出了模型参数与钢筋锈蚀量的计算关系,但是没有考虑箍筋锈蚀率对特征参数的影响。李耀等[13]以加固层数和轴压比为变量,研究了纤维编织网加固混凝土柱的恢复力模型,并提出了相应的特征参数计算公式。刘瑛[14]研究了外包钢加固混凝土短柱在高轴压比状态下的抗震性能,得出了配箍率对构件耗能的影响很大,配箍率越高的构件滞回曲线越饱满,耗能性能也相应更好,但未能就配箍率给出相应的特征参数计算公式。
综上,目前专家学者的研究对象主要侧重于未锈蚀混凝土柱、主筋锈蚀柱和其他材料(如碳纤维布、钢丝网等)加固柱等,针对箍筋锈蚀后钢筋混凝土柱的加固研究的相对较少,且在研究中未能针对箍筋锈蚀后的抗震加固进行深入分析。因此,本文基于外包型钢加固箍筋锈蚀混凝土柱的低周往复荷载试验,选用退化三线型骨架曲线模型,采用线性回归分析法得到骨架曲线特征参数计算公式,建立了加固框架柱的恢复力模型,为此类加固结构的抗震性能分析和可靠性评估提供参考依据。
1 试验概况
1.1 试验设计
试验共设计有7根锈蚀后加固的钢筋混凝土柱和2根未锈蚀未加固的对比柱,共9根模拟框架柱子,尺寸及配筋均一致(单位:mm),具体尺寸及配筋如下图1(a)所示。试件制作时预留有6个标准试块用于测量试件混凝土抗压强度实际值。混凝土设计强度等级为C30,标准条件养护28 d后经测量得轴心抗压强度实际值为36.6 MPa。柱内钢筋的抗拉强度试验值如表1所示。
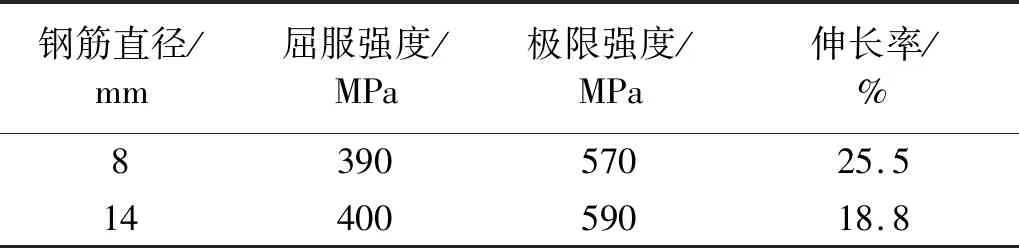
表1 钢筋的抗拉强度试验值Tab.1 Test value of tensile strength of steel bar
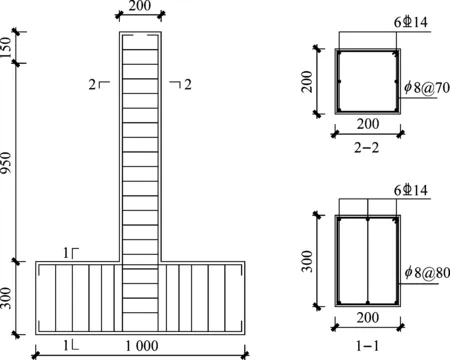
(a) 试验柱配筋详图
1.2 试件锈蚀和加固
试件制作完成后开始通电加速锈蚀,通电锈蚀时间参照文献[15]计算,完成加速锈蚀后从池中取出,之后对锈蚀构件进行外包钢加固,加固方法参考GB 50367—2013《混凝土结构加固技术规范》[16]。加固所用型钢宽度50 mm并在柱与基础根部设置缀板,黏结剂选择环氧树脂黏结和水泥基灌浆料黏结。具体制作参数、锈蚀率及加固方式如表2所示,加固柱详图如图1(b)所示。
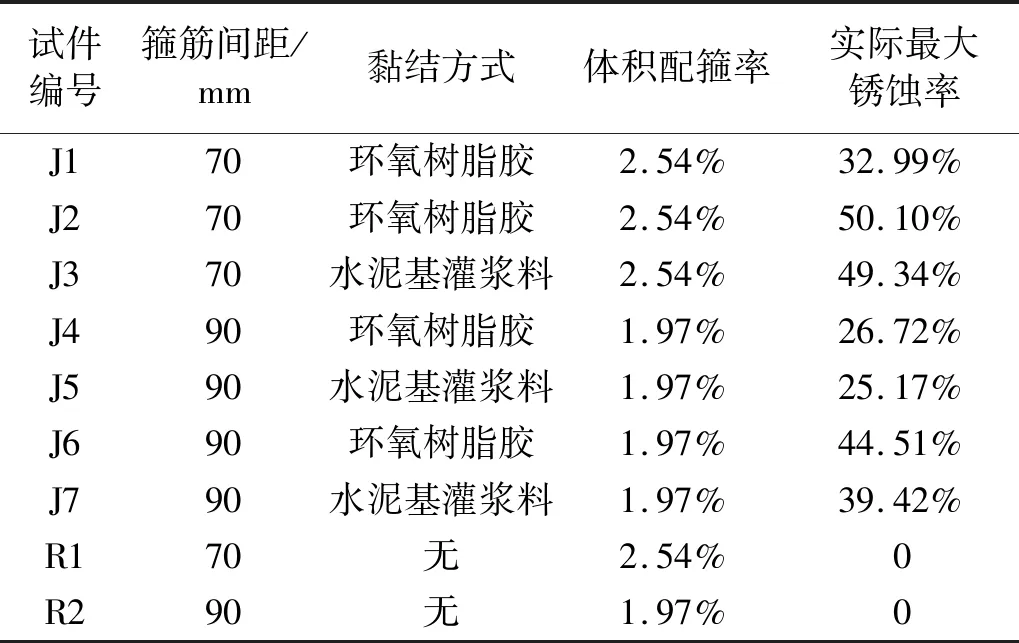
表2 试件加固方式汇总Tab.2 Summary of reinforcement methods of specimens
1.3 试验加载方案及测点布置
试验加载过程参考JGJ/T 101—2015《建筑抗震试验方法规程》,采用位移控制加载,轴压比为0.3,先对试件加载轴力,达200 kN后保持不变,再用水平作动器在距底部基础顶950 mm处施加往复荷载,其加载机制如图2所示。加载时选用水平位移控制,在10 mm位移下以2 mm为一级,每级加载一个循环;在10 mm位移以上,以10 mm为一级,每级位移加载循环三次,观察MTS试验数据,待荷载降到峰值的85%后停止加载,试验结束。

图2 试验加载装置及加载程序图Fig.2 Test loading device and loading program diagram
1.4 试验结果及分析
1.4.1 试件破坏过程
以J1试件为例,其余试件破坏形态及过程如表3所示。限于篇幅此处不赘述。J1试件,加载至水平位移6 mm时,水平荷载大小为70.00 kN,在正面角钢与第一道型钢、第二三道型钢之间产生横向裂缝;加载至水平位移8 mm时,水平荷载大小为77.80 kN;加载至水平位移10 mm时,底部角钢环氧树脂胶开裂,之前出现的裂缝变宽并且横向延伸,侧面第二三、三四道型钢之间出现斜裂缝;加载至水平位移20 mm时,角部锚固角钢焊缝开裂,侧面出现新的斜裂缝,正面产生新的横向裂缝,旧裂缝有不同程度的延伸和加宽;加载至水平位移30 mm时,四角锚固角钢出现不同程度断裂;位移30 mm循环中采集到最大荷载99.26 kN。加载至水平位移40 mm时,侧面第一二道型钢之间产生交叉裂缝,正面锚固角钢上部混凝土保护层部分压酥脱落;加载至水平位移60 mm时,锚固角钢外鼓失效,四面角钢上部混凝土保护层压碎脱落,正面第一道型钢外鼓,分析原因为混凝土压碎挤压导致型钢外鼓。此时不宜继续加载,试验停止。

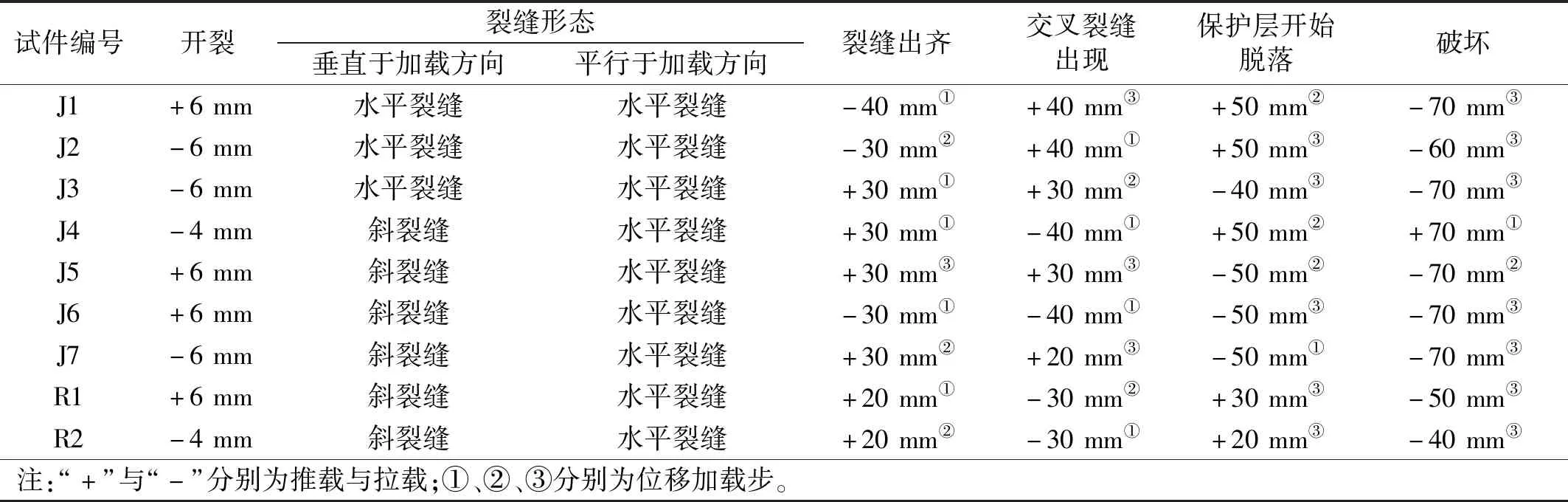
表3 各试件低周往复荷载试验的主要破坏过程Tab.3 Main failure process of each specimen under low cycle reciprocating load test
1.基座;2.反力墙;3.反力架;4.试件;5.力传感器;6.千斤顶;7.滚珠;8.钢板;9.加载垫板;10.小丝杠;11.支撑钢梁;12.支架;13.挡板。
1.4.2 试件破坏及损伤分析
完好试件破坏形态表现为弯曲破坏,经加固后的锈蚀试件破坏形式均为脆性剪切破坏。完好试件主裂缝为横向裂缝,未出现剪切破坏标志性的交叉裂缝和斜裂缝,加载后期未出现混凝土保护层大量脱落,只有柱四角混凝土压酥脱落。加固试件加载过程中以横向裂缝为主,后期破坏阶段,底部锚固角钢焊缝断裂,锚固角钢与第一道型钢之间混凝土保护层被压碎脱落,第一道角钢由于混凝土压碎而被挤压外鼓,最终破坏形态为脆性剪切破坏。达到极限荷载后,环氧树脂有脱落迹象而水泥基灌浆料无此现象。各试件最终破坏情况如表4所示。
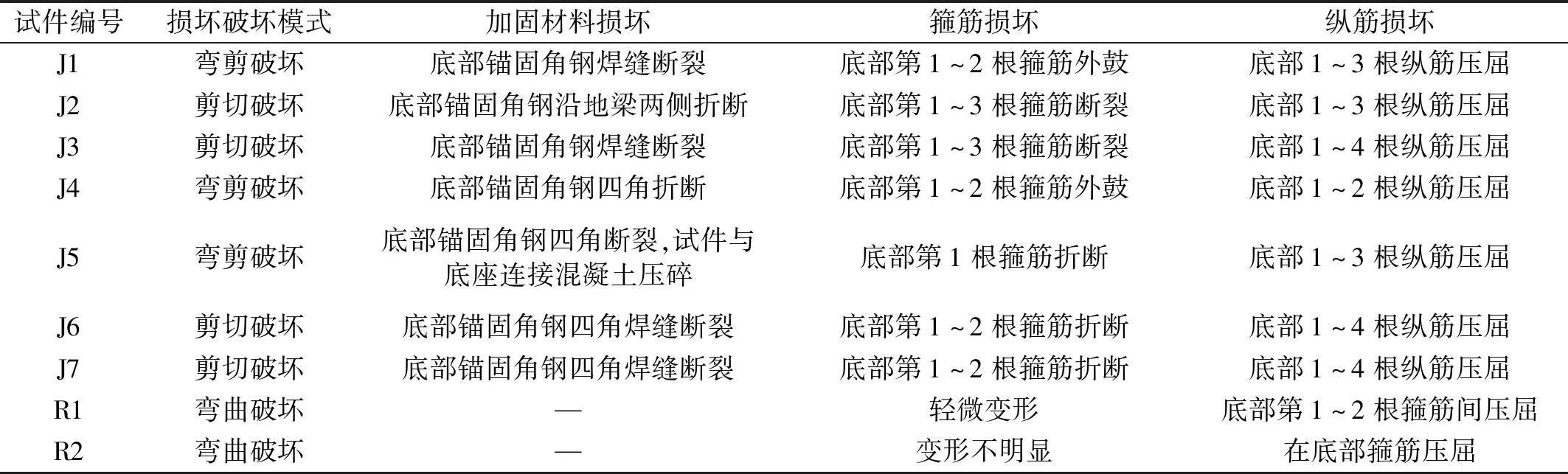
表4 各试件最终破坏模式及关键部位破坏情况Tab.4 Final failure mode of each specimen and failure situation of key parts
通过分析试验结果可以得出以下结论:加固试件出现破坏特征点滞后于完好试件,加载过程中延性特征明显;在锈蚀率、箍筋间距相同的情况下,各加固试件的破坏过程基本一致;环氧树脂胶黏结的外包钢加固试件交叉裂缝出现的加载步晚于水泥基灌浆料黏结的试件,相差一个加载步。此外,外包型钢加固柱均是由于底部1~2根箍筋被折断,核心区混凝土压碎破坏,因角钢外鼓或折断导致抗剪强度降低,最终发生剪切破坏。各试件主要试验数据如表5所示。
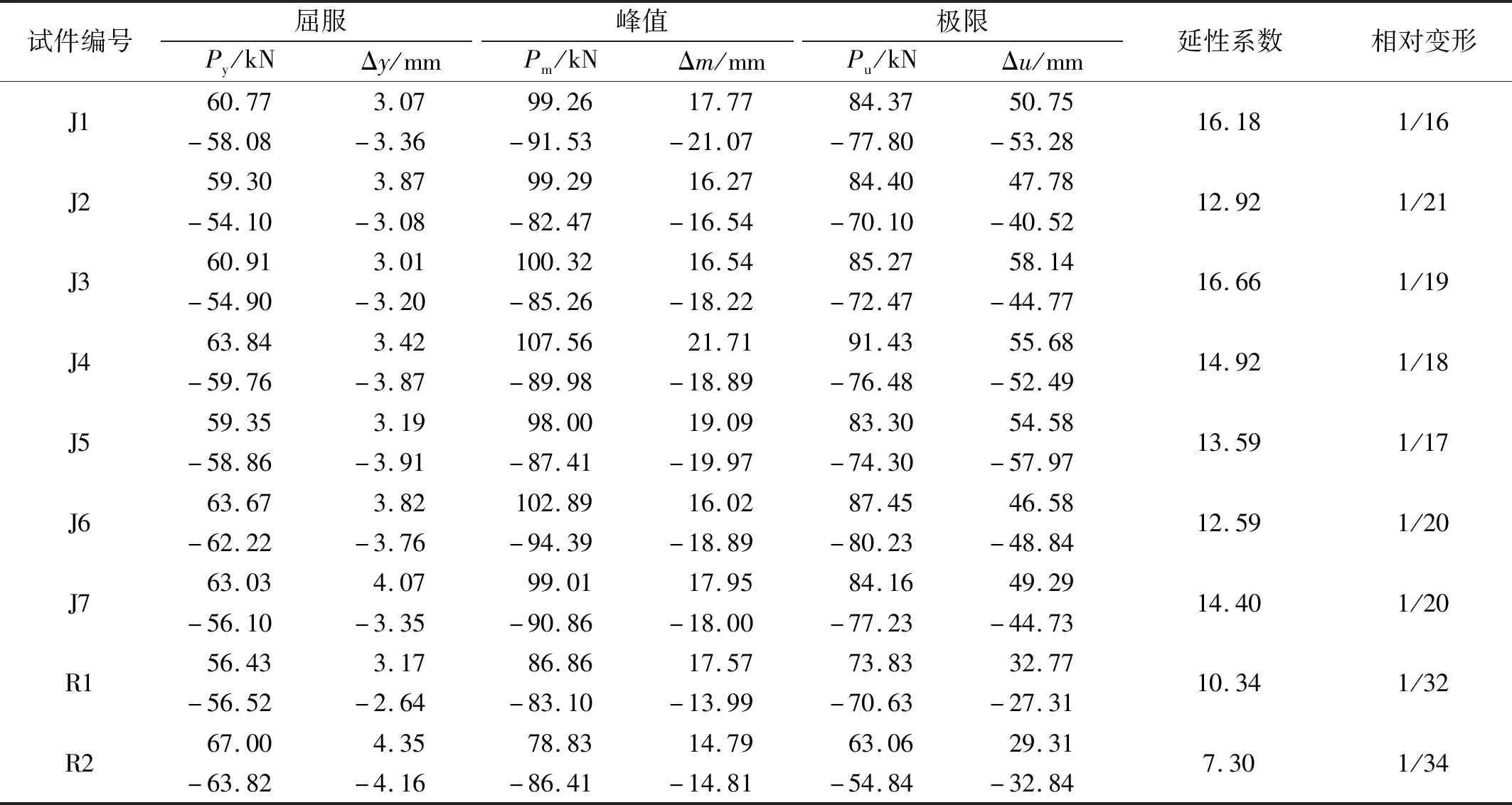
表5 特征点参数和延性系数Tab.5 Feature point parameters and ductility coefficient
2 恢复力模型的确定
随着地震作用或往复加载时间的延长,钢筋混凝土构件的损伤不断累加,导致其承载能力下降,由此造成构件破坏乃至建筑物坍塌。应用于钢筋混凝土结构或构件全过程动力响应分析的恢复力模型正为这种变化提供了理论依据,使用精准的恢复力模型是保证分析和计算得到正确结论的基础。
2.1 骨架曲线的确定
恢复力模型的确定主要包括两方面的内容,即骨架曲线表达形式及其参数的确定和滞回规则的确定。常见的骨架曲线模型中,退化三线型较其他模型(如退化双线型、四线型)考虑了施加往复荷载过程中构件刚度的不断衰退,与实际钢筋混凝土结构表现出的恢复力特征更加贴近。对比不同试件的试验结果,锈蚀构件的骨架曲线在形状上与完好构件基本一致。因此,本文选用退化三线型的骨架曲线模型,如图3所示。具体参数计算见下文。

图3 退化三线型骨架曲线Fig.3 Degenerate trilinear skeleton curve
本文以退化三线型恢复力模型为基础,假定加固锈蚀钢筋混凝土构件与完好构件的骨架曲线模型在形式上是相同的,各段初始加卸载刚度K1、K2、K3参照式(1)~式(3)计算[17]。
(1)
(2)
(3)
2.2 滞回规则的确定
对7个试件的滞回曲线数据进行统计分析,发现加卸载路径大致通过一个“定点”,该定点在0.65Py附近小幅度波动,因此将该定点认为是0.65Py。
综合滞回规律以及文上骨架曲线,得出外包型钢加固锈蚀箍筋柱的P-Δ恢复力模型[18],如图4所示。

图4 建议的恢复力模型Fig.4 Proposed resilience model
该模型中分为弹性段加卸载、强化段加卸载和破坏段加卸载,滞回规则如下:
弹性段对应图4中AD段,组合柱的恢复力在达到A、D前始终处于弹性段范围内,加卸载均沿着AD进行,对应的加卸载刚度始终为K1,不考虑刚度退化情况。
强化段对应图4中AB段和DE段,加固柱的恢复力在正向或负向超过A但未达到B时,从1点开始卸载,沿着直线1-3到达3,再沿着3-4到达4点,接着沿着4-5到达5,随后继续沿着5-7、7-8和8-1完成循环,其中1点和5点互为反向对称点。观察本文中各个滞回曲线,发现各级曲线都会在屈服之前形成一个交汇点,该点对应的恢复力大致为0.65PB,即点4对应的恢复力为0.65PB。另外,根据滞回曲线规律,选定点3对应的恢复力为0.45PB,而1-3和5-7的刚度退化斜率皆为0.8K1。
破坏段对应图4中BC段和EF段,对应加固柱的恢复力从PB降低至PC。破坏段的卸载从9点开始,沿着9-10到达10点,接着沿着10-11达到11点,然后沿着11-4延伸至12点,最后沿着12-14和14-8-9到达9点完成一整圈循环。其中,9点和12点互为反向对称点,11点的恢复力同样为0.45PB,9-10段卸载刚度同样为0.8K1。
3 骨架曲线的计算
对比不同黏结材料粘贴外包钢加固的构件试验数据可知,水泥基灌浆料黏结的试件与环氧树脂胶黏结的试件都在位移4 mm循环时,试件达到屈服荷载,无论锈蚀程度大小,屈服荷载大小几乎没有差别;环氧树脂胶黏结试件比水泥基灌浆料黏结试件峰值荷载约高6%;在达到极限荷载时,加固材料间的黏结材料脱离工作,试件仅由加固材料本身提供约束。因此在后文拟合试验数据给出恢复力模型时,不将黏结材料作为其中变量给出计算公式,仅就箍筋锈蚀率作为变量。
3.1 屈服荷载Py、屈服位移Δy
3.1.1 屈服荷载Py
钢筋混凝土压弯构件的屈服件屈服指的是最大弯矩截面处受拉钢筋屈服或者截面受压区混凝土应变成为极限值。对于剪切型结构层间柱,屈服剪力Py与截面屈服弯矩My有如下关系
(4)

(5)
式中:My为柱截面屈服弯矩,kN·m;H为钢筋混凝土压弯构件的计算高度,mm;As为受拉侧直径14 mm的钢筋截面面积之和,mm2;fy为直径14 mm的钢筋按试验方法标准测得的屈服强度值,N/mm2;fc为混凝土实测轴心抗压强度,N/mm2;h0为截面有效高度,mm;a为受压钢筋中心到受压侧外边缘的距离,mm;n0为试件实际轴压比,n0=0.3;b为截面的宽度,mm;h为截面的高度,mm;η为试件柱身既有混凝土受压区高度系数,且η可按式(6)计算

(6)

式(4)中ξ为修正系数,分析试验结果可以看出,大部分加固试件的屈服荷载在60 kN左右,而理论计算得到的屈服荷载为98 kN,分析认为在试验过程中,判定试件屈服的条件是柱根部有纵筋应变片达到屈服应变,但此时纵筋未必都能屈服,而在理论计算中钢筋均采用实测屈服强度,所以造成理论值偏高。另外,其他因素(如安装套箍回拉环时的松紧程度等)也是可能导致理论与试验屈服荷载差异的一部分原因,因此引入修正系数ξ来减小误差对特征参数计算的影响,ξ为完好构件屈服荷载试验值与理论值的比值,ξ=1/1.63。
3.1.2 屈服位移Δy
根据试验数据可知,加固柱屈服位移与锈蚀率之间呈正相关性。以锈蚀率s和Δy/Δy0分别为x轴和y轴。其中Δy/Δy0为试件J4-J7的屈服位移试验值与计算得到的完好构件屈服位移的比值。如图5所示。

图5 Δy/Δy0与锈蚀率s之间的关系Fig.5 The relationship betweenΔy/Δy0and corrosion rate
根据图5中Δy/Δy0与锈蚀率之间的关系,加固柱的屈服位移Δy按式(7)计算
(7)
3.2 峰值荷载Pm、峰值位移Δm
3.2.1 峰值荷载Pm
由表5试验结果经过origin进行数据拟合分析可以得到峰值荷载与锈蚀率相关关系,如图6所示。其中,Pm/Pm0为加固柱J4-J7的峰值荷载试验值与通过理论计算得到的未加固柱的峰值荷载的比值。
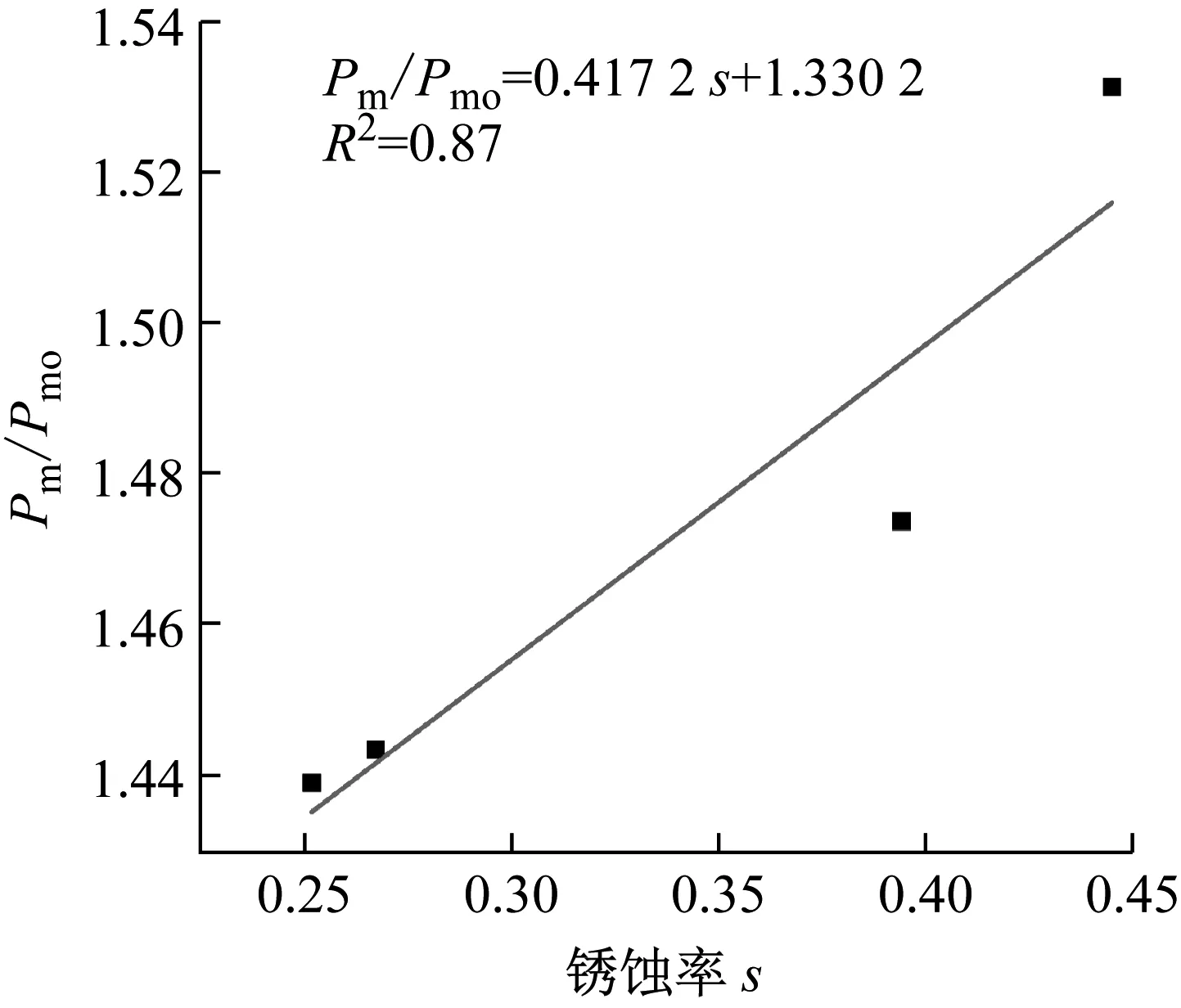
图6 Pm/Pm0与锈蚀率s之间的关系Fig.6 The relationship of Pm/Pm0 and corrosion rate
故根据图6中Pm/Pm0与锈蚀率s之间的关系,加固柱的峰值荷载可以按下式(8)计算
Pm=(0.417 2s+1.330 2)(1.24-0.075ρtαf-0.5n0)Pm0
(8)
式中:Pm为加固柱的理论峰值荷载,kN;ρt为受拉钢筋的配筋率。
3.2.2 峰值位移Δm
参考文献[19],未锈蚀柱的峰值位移可以按式(9)计算
Δm=μmΔy
(9)
其中参数μm为对应于柱极限位移时的延性系数,由下式计算可得:
(10)
式中:λw为柱构件的配箍特征值,λw=αfvρw,αfv为箍筋屈服强度实测值与混凝土轴心抗压强度实测值的比值,ρw为体积配箍率;αw为配箍特征值修正系数,普通矩形圆箍取αw为1.0。
为得到峰值荷载与锈蚀率和体积配箍率之间的关系,分别以锈蚀率s和体积配箍率ρw为自变量,以Δm/Δy0为应变量,通过SPSS软件进行多因素线性回归分析。根据SPSS各试件的峰值位移Δm可按式(11)计算。
Δm=(5.396 0ρw-2.138 0s+3.473 0)Δy0
(11)
3.3 破坏荷载Pu、破坏位移Δu
3.3.1 破坏荷载Pu
参考JGJ/T 101—2015《建筑抗震试验方法规程》,当试件的水平承载力小于加载过程中的最大荷载的85%时,试验停止加载,此时的荷载即为试件的破坏荷载,故加固柱的破坏荷载可按式(12)计算
Pu=0.85Pm
(12)
3.3.2 破坏位移Δu
为了得到各试件的破坏位移与锈蚀率之间的关系,分别以锈蚀率s和各试件的Δu/Δy为x轴和y轴建立坐标系,如图7所示。其中,Δu/Δy为各试件的破坏位移实测值与其屈服位移理论值的比值。由试验结果可知,加固试件延性与锈蚀率呈负相关性。

图7 Δu/Δy与锈蚀率的关系Fig.7 The relationship of Δu/Δy and corrosion rate
根据各试件的Δu/Δy与锈蚀率之间的关系,各试件的Δu可按式(13)计算
Δu=(-6.324 6s+9.963 4)Δy
(13)
3.4 计算骨架曲线与试验骨架曲线的比较
外包型钢加固混凝土柱试件骨架曲线特征参数计算值,如表6~8所示。
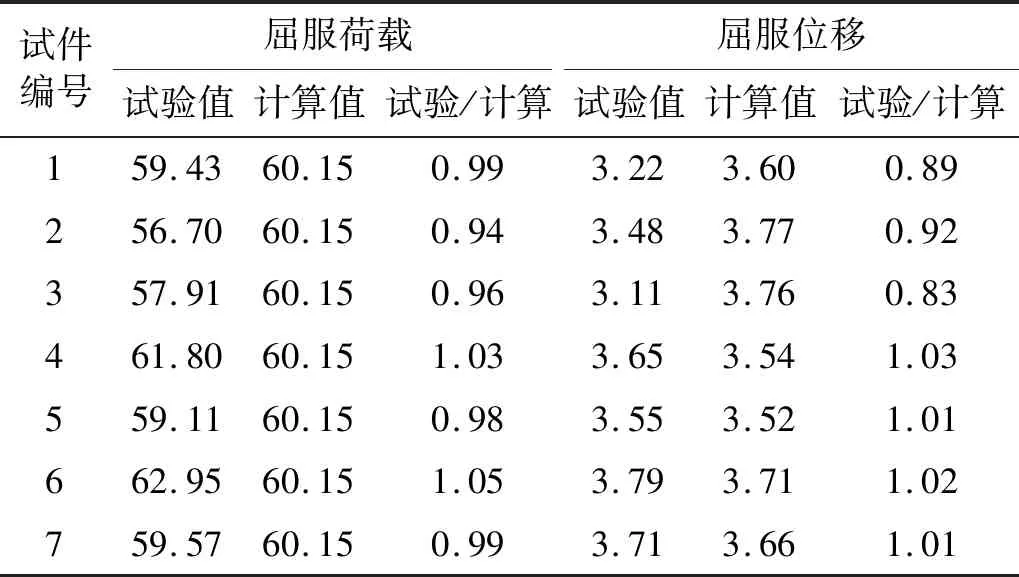
表6 屈服荷载和屈服位移试验值与计算值对比Tab.6 Comparison of yield load and displacement between measurements and calculations

表8 破坏荷载和破坏位移试验值与计算值对比Tab.8 Comparison of failure load and displacement between measurements and calculations
各加固试件试验与计算得出的骨架曲线图以及完好柱骨架曲线图,如图8所示。
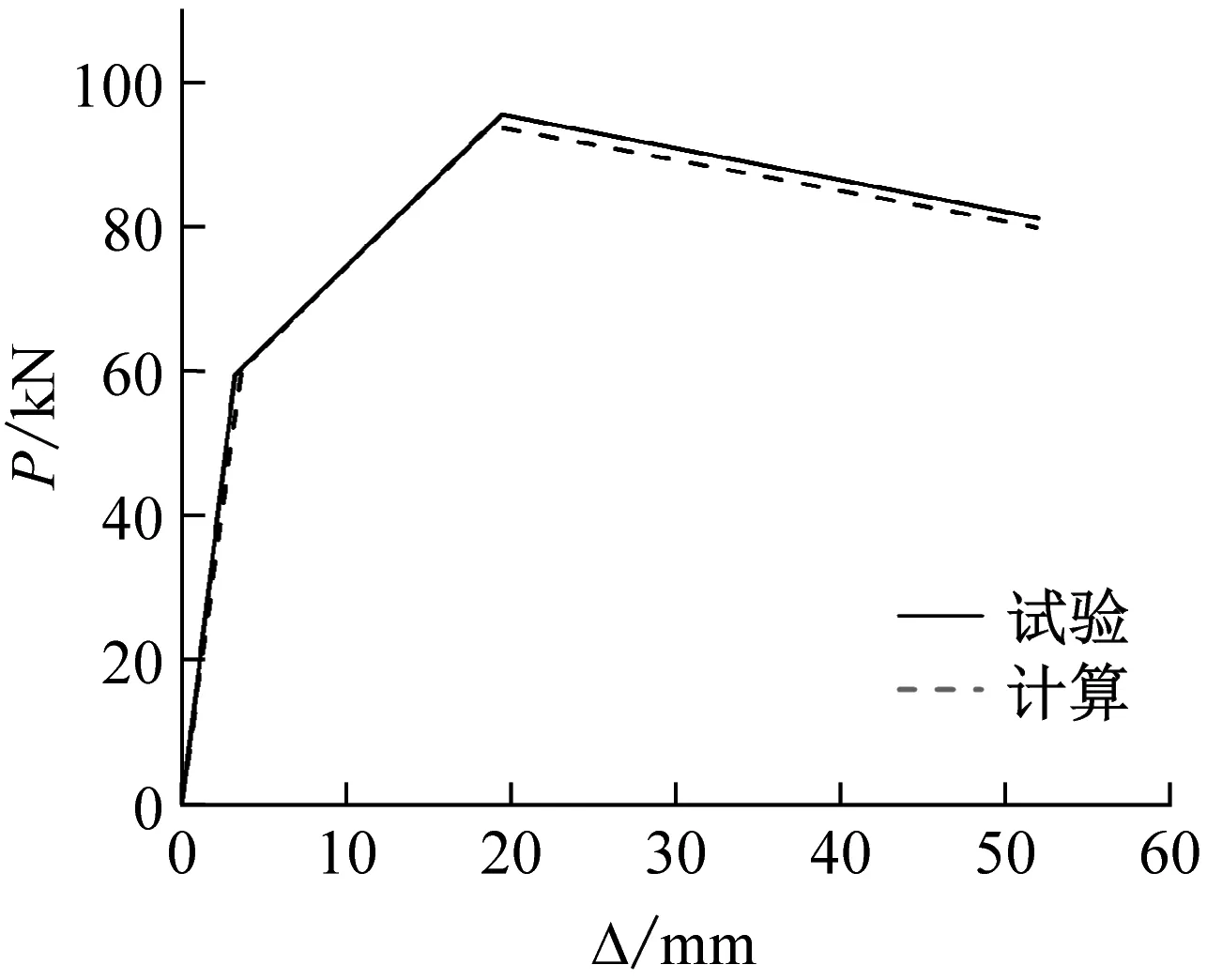
(a) 试件J1
对比计算值与试验值得到的骨架曲线,可以看出:计算结果总体上与试验结果吻合较好,但仍有部分数据与计算值有偏差,这是由于试验存在一定误差,以及计算过程中忽略了部分次要因素导致的。另外,对于恢复力模型中特征参数的计算至今没有统一的定值计算方法,因此这些因素都可能引起误差,但同样这些因素也可以作为后续进一步研究考虑的内容。
4 滞回曲线的计算
为验证文章拟合公式得出的骨架曲线的准确性,分别绘制各试件计算滞回曲线与试验所得滞回曲线的对比图以及完好试件的滞回曲线图,列于图9。由对比图9可以看出,各试件计算得出滞回曲线与试验所得吻合较好,能够反映加固柱的滞回规律,为以后此类柱的恢复力模型计算提供依据。
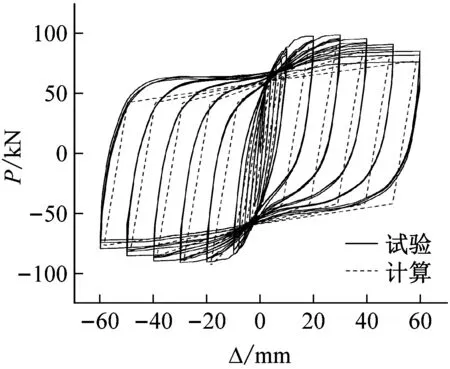
(a) 试件J1
5 结 论
在目前已有的试验的基础上对本次试验柱的恢复力模型进行分析可得出的主要结论如下:
(1) 对于锈蚀率在30%左右的试件,用环氧树脂胶黏结外包钢加固比水泥基灌浆料黏结效果略好,体现在水泥基灌浆料黏结的试件,交叉斜裂缝出现时间较环氧树脂胶黏结加固试件早一个荷载步,环氧树脂胶黏结加固材料与试件协同工作能力较好,但对于锈蚀率大于45%的试件,两种黏结方式对抗震性能几乎没有影响。
(2) 对试验数据进行拟合分析,引入对特征参数影响较大的箍筋锈蚀率s和体积配箍率ρω,在完好柱理论公式的基础上进行修正,得到了外包型钢加固柱的恢复力模型特征参数计算公式。结果表明计算值与试验值最大误差在15%以内,特征参数具体可按下列公式计算:
Δm=(5.396 0ρw-2.138 0s+3.473 0)Δy0
Pu=0.85Pm
Δu=(-6.324 6s+9.963 4)Δy
(3) 综合骨架曲线、滞回规则,建立了适用于外包型钢加固锈蚀钢筋混凝土柱的恢复力模型,对比理论计算和试验得到的骨架曲线与滞回曲线,二者吻合较好,能很好地反映外包型钢加固柱的滞回特性,为此类柱恢复力模型的计算提供参考。

