基于响应面法的新型再生骨料透水混凝土性能预测研究
谷俊峰 杜晓 魏献法 陈守开 张政男





关键词:新型再生骨料透水混凝土;抗压强度;透水系数;响应面法;预测
再生骨料透水混凝土(RecycledAggregatePerviousConcrete,RAPC)是废混凝土资源化利用的产物,是指天然骨料被再生骨料取代制备出的透水混凝土[1-3]。它与再生资源的循环利用有机结合,且透水透气性比普通透水混凝土更好。在当前绿色可持续发展、海绵城市建设的时代主题下,RAPC的发展与应用前景非常广阔,但在同配比条件下,会出现强度与渗透性成负相关关系的现象[4-5]。因此,本文提出了一种新型再生骨料透水混凝土(InnovativeRecycledAggregatePerviousConcrete,I-RAPC),即将普通RAPC内部原本均匀分布的孔隙集中成上下连通的管道,并在管道中嵌入管材,区别于传统的再生骨料透水混凝土,它具有高强度、高透水的特点。牛志刚等[6]通过建立孔隙率与暴雨等级的定量关系确定出透水混凝土的最佳孔隙率范围,又基于孔隙率与强度之间的关系,明确混凝土强度等级,设计制备了新型再生透水混凝土。研究表明新型再生透水混凝土满足道路混凝土对抗压、抗弯拉强度的要求,且具有优异的抗暴雨内涝性。
本文探究不同管孔数量、直径、材料对I-RAPC强度性能与渗透性能的影响规律。对于多因素交互影响的研究可采用响应面分析法(ResponseSurfaceMeth⁃odology,RSM),它将试验设计和数学建模有效结合,通过对具有代表性的局部各试验点进行试验并得到数据,回归拟合代表性数据点数据得到全局范围内因素与结果间的函数关系式,并且通过优化可取得各因素对响应结果的最优水平值[7-9]。吴永根等[10]采用响应面分析法研究了水胶比、胶凝材料用量、砂率等自变量及其交互作用对混凝土7d抗折强度的影响,发现胶凝材料用量和砂率的交互作用最显著;石振武等[11]基于RSM研究了钢纤维长径比、钢纤维体积掺入率和水胶比对混凝土耐磨性的影响,通过建立试验模型并进行最优化预测,认为理论分析结果与实际情况相一致。徐仁崇等[12]通过RSM对透水混凝土配合比进行了方案设计和试验结果分析,发现在成型方式相同的情况下,水泥用量、骨料级配和粒径是影响其透水性和抗压强度的主要因素,并得到了透水混凝土的优化配合比。因此,本文采用RSM设计试验并建立正面、侧面抗压强度及透水系数的响应模型,分析了管孔特征(管孔数量、直径、材料)及交互作用对I-RAPC关键性能(强度和透水性能)的影响,并对优化结果进行试验验证,为I-RAPC的创新发展及拓宽应用提供科学有效的理论支撑。
1试验材料与方法
1.1材料及配合比
本试验采用的再生粗骨料粒径为4.75~9.50mm,骨料表观密度、堆积密度分别为2595、1245kg/m3;细骨料采用细度模数为2.9的天然河砂;水泥为天瑞集团水泥有限公司生产的P·O42.5普通硅酸盐水泥;水为自来水;管材分为竹管、亚克力管和混凝土管。参照《水工混凝土配合比设计规程》(DL/T5330—2015)设计IRAPC配合比(见表1),设计强度为C30。
1.2试验方法
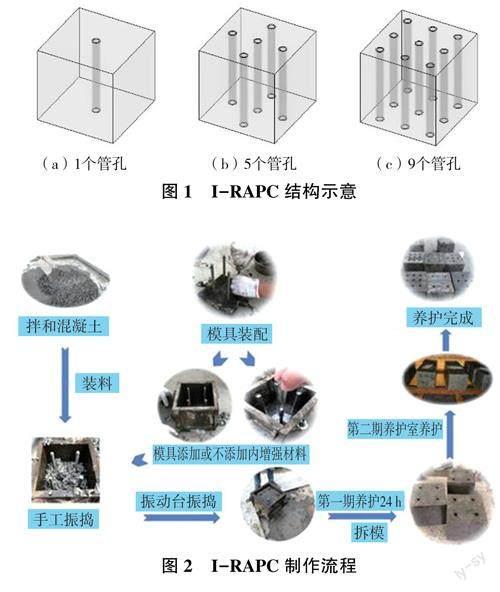
新型再生骨料透水混凝土是在传统透水混凝土的基础上进行改进,最后成型结构见图1。本试验设置的管孔数目为1、5、9个。I-RAPC改变了传统透水混凝土中孔隙的分布形式,将原本均匀分布的孔隙集中成上下连通的细长管道,兼具较高强度和透水性能,且简化了透水混凝土的孔隙结构,不易造成堵塞。本试验I-RAPC制作流程如图2所示。
本试验测试指标包括I-RAPC强度性能和渗透性能,试件均为150mm×150mm×150mm标准立方体。
1.2.1强度性能
由于管孔会导致不同受压面的抗压强度存在差异,因此试验中测试了正面、侧面两种抗压强度,其中正面、侧面抗压强度分别是指垂直管孔、平行管孔受压面所测强度。以试块的正面、侧面为受压面,在DY-3008DX电液伺服微机控制压力试验机上完成。参照《普通透水混凝土力学性能试验方法标准》(GB/T50081—2002),将荷载加载速度设置为0.5MPa/s,试验结束后根据式(1)计算I-RAPC抗压强度:
1.2.2透水性能
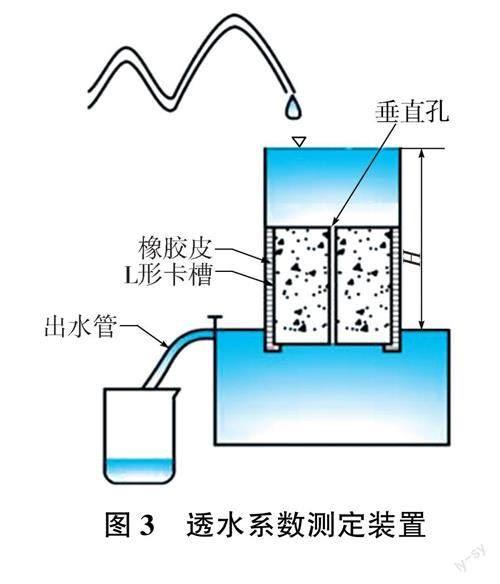
透水系数是表征I-RAPC透水性能优劣的直观指标,本试验基于达西定律定水头法,采用自制的透水装置(见图3)测定,并根据式(2)计算I-RAPC的透水系数:
1.3响应面设计及试验结果
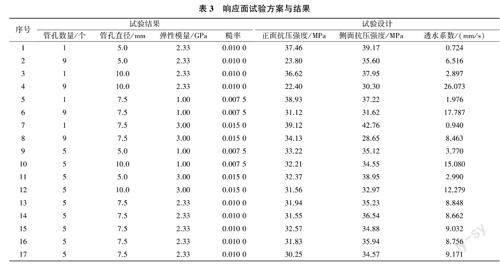
采用Design-Expert10.0.3軟件使用Box-BehnkenDesign(BBD)功能对其进行响应面设计分析,具体影响因素与水平取值见表2。响应面分析法试验设计方案与试验结果见表3。
2RSM响应模型
2.1响应面模型构建与分析
根据Weierstress多项式最佳逼近定理,大多函数都可以用多项式去逼近,多项式近似模型可处理相当广泛的非线性问题,因此在实际应用中,无论自变量和因变量关系如何,都可以采用多项式近似模型进行分析[13-15]。本文分别对正面、侧面抗压强度和透水系数进行多元回归分析,得到多元回归方程:
对以上回归方程进行方差分析及显著性检验,结果见表4。上述模型P值均小于0.05,即均通过显著性检验,可用于后续优化设计;失拟项为模型与试验拟合程度,即二者差异程度。模型失拟项的P值均大于0.05,表明模型失拟项差异不显著,即试验数据与模型不相关程度不显著,模型可信。F值代表模型对响应面的影响程度,在正面、侧面抗压强度响应模型中,F(x)<F(d)<F(E),因此管孔数量为最敏感因素,对强度的影响最大,其次是管孔直径,最后是管材的弹性模量;在透水系数响应模型中,F(d)<F(x)<F(n),因此管孔直径成为最敏感因素,其次为管孔数量和糙率,糙率的敏感程度最低。
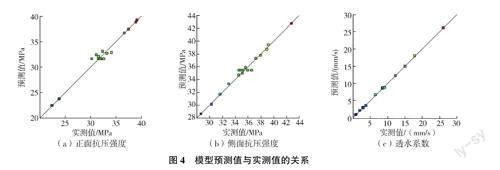
I-RAPC正面、侧面抗压强度及透水系数回归方程误差统计分析结果见表5。模型决定系数R2分别为0.9757、0.9840、0.9993,当R2>0.9时表明模型的预测值与实测值的吻合度较高[16];模型校正决定系数(AdjR2)分别为0.9514、0.9634、0.9983,即模型回归方程可分别模拟95.14%、96.34%、99.83%的响应值变化,且AdjR2与模型预测决定系数(PredR2)差值绝对值分别为0.0613、0.0229、0.0408,其差值小于0.2时可认为除给定因素外没有其他影响因素,说明回归模型能充分说明工艺问题[17]。另外,精密度(AdeqPreci⁃sion)分别为23.496、28.206、113.460,变异系数(C.V.)分别为3.03%、1.84%、3.27%,精密度均远大于4,变异系数均小于10%,表明模型的精确度和可信度高[18]。
2.2响应曲面及等高线图
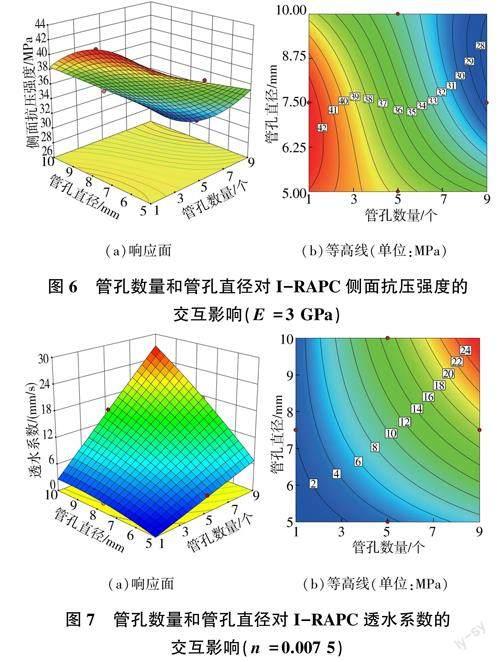
利用响应面分析法建立的三维立体响应曲面和等高线图可直观反映出试验因素间的交互作用,即在某个因素为某一定值时,另外两个因素间的交互作用对响应值的影响。等高线的形状可反映出交互效应的强弱,椭圆形表示两因素间的交互作用显著,而圆形则与之相反。由于4个影响因素中,对I-RAPC强度和透水系数影响最大的是管孔数量与管孔直径,因此本部分仅讨论管孔数量与管孔直径对I-RAPC强度和透水系数的交互影响,其响应曲面及等高线图见图5~图7。
图5为管孔数量和管孔直径对I-RAPC正面抗压强度的交互影响(E=3GPa)的结果,I-RAPC的正面抗压强度随管孔数量增加呈降低趋势,常规透水混凝土的强度性能也是随孔隙率的增大而降低[19-20];同时,混凝土管孔作为3种管孔材料中弹性模量最大的管道,其对应的抗压强度比另外两种管孔(竹管孔、亚
克力管孔)的抗压强度高。图6为管孔数量和直径对I-RAPC侧面抗压强度的交互影响(E=3GPa),管孔数量和直径越小,侧面抗压强度越高,管孔数量、直径的交互作用更为显著。图7为管孔数量和直径对IRAPC透水系数的交互影响(n=0.0075),管孔数量和直径对透水系数的影响重大,这两个因素的交互作用显著,且这两个因素的值越大,透水系数越大。此外,通过观察等高线在坐标轴上分布的密集程度,可以发现管孔数量和管孔直径对I-RAPC正面、侧面抗压强度以及透水系数有显著影响,且等高线曲率越大二者间的交互作用越显著。
2.3模型优选及验证
利用软件优化选项功能便可求解响应目标的最优值。因此,以响应值最大为最终目的,设定抗压强度输出范围为0~45MPa,透水系数输出范围为0~30mm/s,则正面、侧面抗压强度输出结果的条件为管孔数量为1个、管孔直径为5mm、管孔材料弹性模量为3GPa,透水系数输出结果的条件为管孔数量为9个、管孔直径为10mm、管孔材料糙率为0.0075。得出的优选结果见表6、表7和表8,優化的模型合适性均较好。模型优化结果中,正面、侧面抗压强度优化结果分别为40.853、41.911MPa,实测正面、侧面抗压强度分别为41.460、43.880MPa,与模型优化结果的绝对误差分别为0.607、1.969MPa,相对误差分别为1.46%、4.49%;透水系数优化结果为27.233mm/s,实测透水系数为27.144mm/s,与模型最优化结果的绝对误差为0.089mm/s、相对误差仅为0.33%,精度较高。试验结果与模型优化预测结果相近,表明基于响应面分析法进行试验设计、分析与目标预测具有现实意义。
3结论
1)基于RSM建立了以I-RAPC正面、侧面抗压强度和透水系数为响应值,管孔数量、直径及材料为响应因子的优化模型,通过多元回归近似方程拟合及方差分析和误差统计分析发现,正面抗压强度、侧面抗压强度、透水系数模型R2分别为0.9757、0.9840、0.9993,模型的预测值与实测值的吻合度较高;模型AdjR2分别为0.9514、0.9634、0.9983,模型回归方程可分别模拟95.14%、96.34%、99.83%的响应值变化。
2)对于正面、侧面抗压强度,管孔数量对强度的影响最大,其次是管孔直径,最后是管材的弹性模量;对于透水系数,管孔直径对透水系数影响最大,其次为管孔数量和糙率,糙率对透水系数影响很小,但表现出糙率越大透水系数越小的规律。
3)通过模型优选求解响应值的最优值,得到与之对应的试验条件,并进行试验验证,正面、侧面抗压强度最优值分别为40.853、41.911MPa,实测正面、侧面抗压强度分别为41.460、43.880MPa;透水系数最优值为27.233mm/s,实测透水系数为27.144mm/s。试验结果与模型优化预测结果相近,表明基于响应面分析法进行试验设计、分析与目标预测具有现实意义。

