爬壁机器人脚爪的设计与分析

余淑荣,龚宇强,张来喜,吴明亮

(兰州理工大学机电工程学院,甘肃 兰州 730050)

在自然界和人类生存环境中,大多数墙壁均是粗糙多尘的。随着科学技术的不断进步与发展,仿生钩爪式抓附结构的爬壁机器人应运而生,并成为国内外研究的热点。多年来,国内外学者对钩爪式抓附结构爬壁机器人的研究取得了突破性进展。

2005年美国斯坦福大学的Asbeck和Kim等[1-3]根据昆虫和蜘蛛的爬行机制研制出首台钩爪式爬壁机器人SpinybotⅡ,该机器人能够可靠地在灰泥或粗糙的混凝土壁面上攀爬。Dickson等[4-5]为解决爬壁机器人结构鲁棒性不足的问题,研究出了一款微型两足机器人BOB(bipedal oscillating robot),此机器人控制方案简单,机身轻,通过对脚掌上类似于RISE机器人的柔性钩爪结构进行改进,实现了其在粗糙竖直壁面上的攀爬[6]。哈尔滨工程大学的陈东良等[7]设计了一种六足钩爪式爬壁机器人,此机器人足部可根据壁面粗糙程度自行调整起伏,具有自适应性。西安理工大学的刘彦伟等[8]根据毛虫腹足趾钩阵列对抓原理,设计了一款仿生爪刺对抓式履带爬壁机器人,此机器人能够在粗糙壁面上竖向、横向和倒挂爬行。同时,为了使爬壁机器人具有一定的越障能力,刘彦伟等[9]还研究出一种仿生爪刺式双足爬壁机器人,通过测试,验证了机器人设计的有效性。

本文提出一种密集阵爪刺式的脚爪抓附结构,此脚爪具有柔性基底,可增加抓附在粗糙表面的爪刺数量,提高足部载重,使脚爪可以稳定抓附在壁面上,拓展了爬壁机器人在复杂墙壁环境中的应用范围,具有重要的工程价值。

1 影响抓附性能的相关参数分析

通过分析可知,影响阵列爪刺式脚爪抓附壁面性能的因素包括爪刺的排列密度、爪刺伸出基底的长度和爪刺尖端直径等参数。

1.1 爪刺的排列密度

为了方便制造和安装密集阵爪刺式脚爪,本文将爪刺均匀地排列在脚爪上。当爪刺排列密度较大,即相邻爪刺之间距离较小时,在脚爪抓附壁面的过程中,密集阵中各爪刺将互相影响,具体情况如图1(a)、(b)和(c)所示。

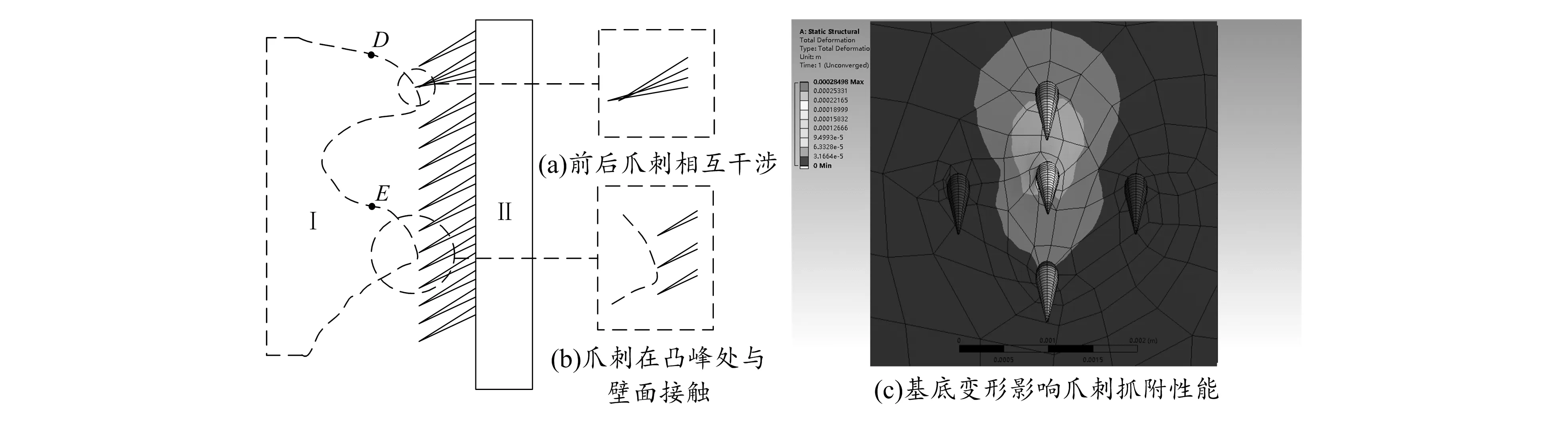
图1 密集阵中各爪刺互相影响示意图

图1中的Ⅰ代表粗糙壁面上凹凸不平的凸起,Ⅱ代表密集阵爪刺式脚爪。从图1(a)中可以看出,随着脚爪向下滑动,若脚爪上的爪刺之间距离过近,后面发生转动的爪刺很可能触碰到前面没有抓到壁面的爪刺,从而产生干涉,使原本已经抓附在壁面上的爪刺发生脱离壁面的现象。

在分析图1(b)之前,本文先介绍轮廓单元的概念,即轮廓单元是指一个轮廓峰与一个轮廓谷的组合,如图1中点D～点E的虚线部分。

从图1(b)中可以看出,当爪刺之间距离过近时,在一个轮廓单元内,最先接触壁面的那根爪刺一定在轮廓单元的凸峰附近与壁面接触。当爪刺与壁面接触之后,壁面便会对其产生一个垂直于壁面向外的力来阻止脚爪进一步向墙面移动,这样就使其他爪刺无法进一步与壁面接触。这导致脚爪上的爪刺在壁面上的抓附都很浅,使脚爪的重心提高而无法稳定地抓附在壁面上。

从图1(c)中可以看到,如果爬壁机器人脚爪上的某一根爪刺先抓附到壁面上,并发生变形时,该爪刺的基底部分将产生变形,当爪刺之间距离过近时,相邻爪刺将因进入该爪刺的基底变形部分而受到影响,从而降低相邻爪刺的抓附性能。

假设当爪刺与壁面之间的夹角为γ0时,基底所发生的弹性形变量将超出其所能承受的最大形变量,则此时γ0为爪刺稳定抓附壁面时与壁面形成的最大夹角,对应的S1为爪刺之间最小距离,如图2所示。当阵列爪刺之间的距离大于S1时,爬壁机器人脚爪上后排爪刺在抓附壁面的过程中将不会对前排爪刺产生影响。

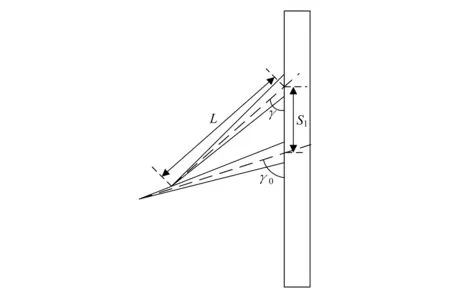
图2 爪刺之间相互影响第一种情况示意图

根据图2可得:

(1)

式中:L为爪刺伸出基底的长度;γ为爪刺安装在基底上时与壁面间的夹角。

同时,将壁面轮廓单元的最大宽度设为S2,当爪刺之间间距大于轮廓单元的最大宽度S2时,可避免发生图1(b)中的情况。由于测量轮廓单元的最大宽度在实际操作中有一定困难,美国斯坦福大学的Asbeck等[3]提出粗糙壁面上各凸起之间的间距分布近似概率论中的指数分布,即:

P{X≤x}=F(x)=1-e-λx,x≥0

(2)

式中:P{X≤x}为粗糙壁面各凸起距离小于x的概率;X为随机变量;x为粗糙壁面各凸起之间的距离,而粗糙壁面各凸起之间的平均距离为1/λ,方差为1/λ2,其中λ>0为指数分布参数;F(x)为随机变量X的分布函数。在取样长度lr内,RSm为轮廓单元的平均宽度,故RSm=1/λ。当测量出取样长度lr内轮廓单元的平均宽度RSm后,通过公式(2)求得在P{X≤x}≥0.98时的x值就可以近似地看成是轮廓单元最大宽度S2。

最后,通过ANSYS有限元仿真软件对脚爪基底的变形量进行仿真分析,仿真结果如图3所示。

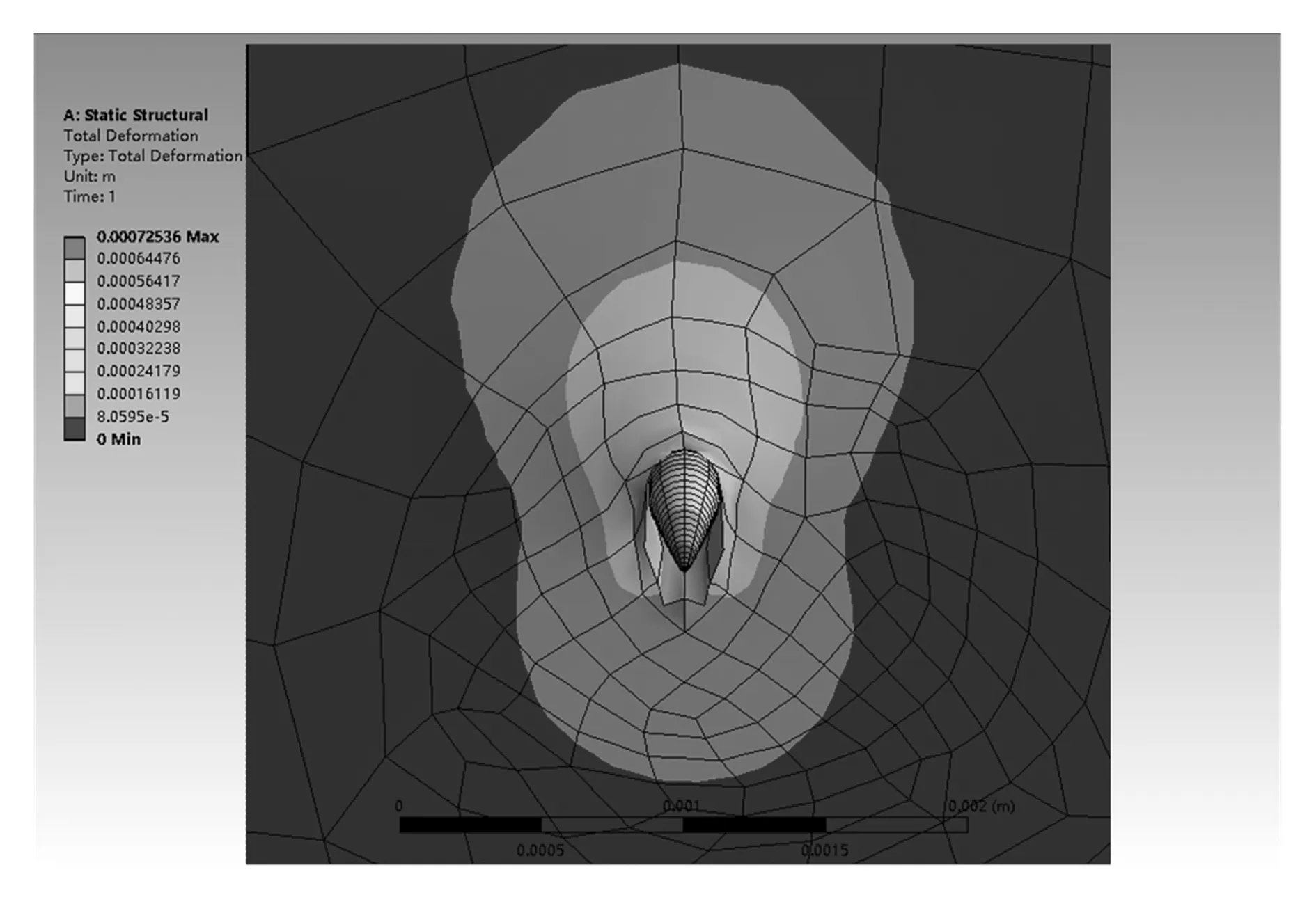
图3 基底变形量仿真结果

从图3中可以看出,基底在受到爪刺的作用后,会以爪刺为中心,分别在爪刺的前后两侧产生两个扇形的变形区域。假设在爪刺尖端施加一个保证基底不发生失效的最大力Fmax时,两扇形区域边界距爪刺中心的最远距离为S3,则爪刺之间间距大于S3就能保证不发生该情况。

综合以上分析可知,当脚爪上的阵列爪刺之间间距S大于S1、S2和S3中的最大值,就能保证无论在上述哪种情况下,阵列爪刺均能相互独立地抓附在壁面上。本文实验均在24目砂纸所制作的模拟壁面上进行,经过计算与仿真分析得出:当阵列爪刺之间的间距等于4.7 mm时,刚好能保证阵列爪刺在抓附模拟壁面的过程中互不影响。

1.2 爪刺伸出基底的长度

脚爪上爪刺伸出基底的长度L直接决定爪刺能否抓附在壁面上。绘制爪刺抓附到壁面轮廓谷的示意图(图4),并以此分析L的合理值。

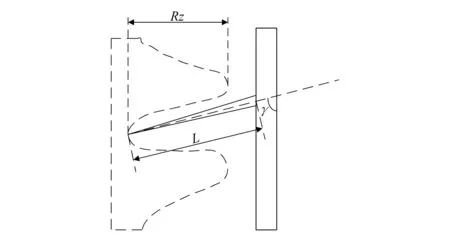
图4 爪刺抓附到壁面轮廓谷示意图

从图4中可以看出,要想使爪刺可以接触壁面轮廓谷的谷底,则L在垂直于墙面方向的投影应大于等于轮廓的最大高度Rz,即:

Lsinγ≥Rz

(3)

由方程(3)可得:

(4)

由方程(4)可知,当L=Rz/sinγ时,爪刺就可以接触到壁面的轮廓谷谷底。在保证爪刺能接触到轮廓谷谷底的情况下,L越短越有利于爬壁机器人稳定地抓附壁面,故L的值取为Rz/sinγ。

美国斯坦福大学的Asbeck等[3]也指出粗糙壁面上各凸起的高度分布同样可近似成概率论中的指数分布,其分布函数与式(2)相同。通过等效替代,求得在概率大于0.98时的轮廓宽度就可以近似地看成是轮廓单元最大宽度Rz。

本文以24目砂纸的轮廓偏距绝对值的算术平均值Ra(约为250 μm)计算Rz,将λ=1/Ra代入式(2)中求得壁面凸起的高度小于1 mm的概率为0.981 68,因此本文取Rz的值为1 mm,故爪刺伸出基底长度的最佳值应为Rz/sinγ=1.15 mm。

1.3 爪刺的尖端直径

通过实验与观察,脚爪上爪刺的尖端直径与壁面凸起高度之间的关系如图5(a)、(b)所示。若爪刺尖端直径远大于壁面凸起的高度,则脚爪无法抓附在壁面上,所以本文假设爪刺尖端直径大小与壁面凸起的高度相当,且壁面足够粗糙。

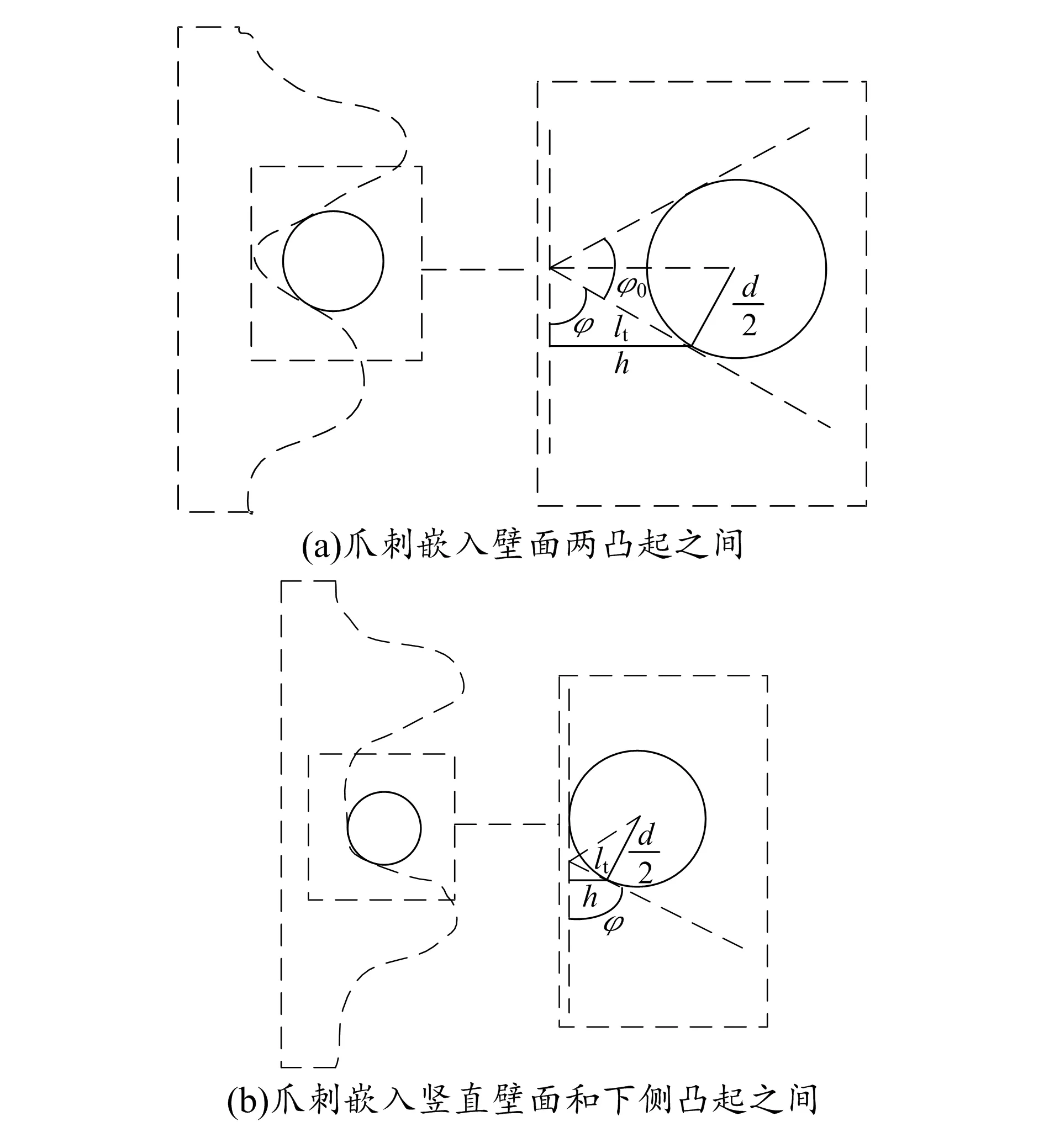
图5 爪刺尖端直径与壁面凸起高度之间的关系图

图5(a)中壁面两凸起之间相距较近,爪刺尖端夹在两凸起之间,并能够嵌入两凸起之间最深处。将爪刺尖端与壁面两凸起接触点处的切线延长至相交,两条延长线的夹角为φ0,爪刺与下凸起接触点处的切线倾角为φ。由于爪刺与壁面的接触处接近两凸起之间的最深处,故本文假设两凸起之间的最深处到爪刺尖端与两凸起接触处点的倾角不变。从图5(a)中可以看出,接触点与凹谷最深处的高度差等于接触点与两切线交点的高度差h,接触点到两切线交点的距离为lt,爪刺尖端直径为d,此时有:

(5)

(6)

整理等式(5)和(6)得到:

(7)

因为壁面轮廓凸起的高度呈指数分布,所以将x=h代入指数分布函数式(2)得到:

(8)

此时壁面轮廓凸起的高度大于h的概率为:

(9)

把λ=1/Ra代入概率分布函数式(9)得:

(10)

在图5(b)中,壁面两凸起之间相距较远,爪刺只与竖直墙面和下侧凸起相接触。此时式(5)不变,式(6)变为:

(11)

整理方程(5)和(11)得:

(12)

同样,将x=h代入指数分布函数式(2)得到:

(13)

此时壁面轮廓凸起的高度大于h的概率为:

(14)

把λ=1/Ra代入概率分布函数式(14)得:

(15)

分析公式(10)与(15)发现,壁面凸起轮廓高度大于h的概率分别与Ra、d、φ和φ0有关。X>h的概率随着Ra与φ0的增大而增大,随着d与φ的增大而减小,其中Ra越大则表示壁面凸起的平均高度越高,即壁面凸起轮廓的高度大于爬壁机器人爪刺可抓附凸起的最小高度h的概率也就越大。由于爬壁机器人可抓附的壁面凸起数量较多,且每个凸起之间的φ与φ0呈随机分布,无法人为将其改变,故本文不做分析。由以上分析可知,爬壁机器人爪刺是否可以稳定抓附在壁面凸起上主要与Ra和d相关。

观察发现,爪刺尖端在24目砂纸上的抓附结果基本符合图5(b)的情况。将24目砂纸的Ra值代入式(15)中,求得P{X>h}≥0.98时的爪刺尖端直径d的最佳值约为34 μm。

2 脚爪所能承受最大载荷的实验分析

在爬壁机器人脚爪抓附壁面的过程中,爪刺的排列密度、爪刺伸出基底的长度及爪刺尖端直径均会对脚爪所能承受的载荷产生影响。本文为了准确模拟脚爪在粗糙壁面上的实际受力情况,将所设计的脚爪直接放在模拟壁面上,通过对脚爪逐渐增加负载的方法来测量脚爪所能承受的最大载荷,且为防止所测值具有偶然性,在由24目砂纸制作的模拟壁面(如图6所示)的各处均进行实验。

图6 模拟壁面实物图

为保证脚爪稳定地抓附在壁面上,同时不让金属块从脚爪上翻落,实验中模拟壁面与竖直面之间的夹角取为5°,如图7所示。由于模拟壁面倾角很小,所以并不影响实验验证脚爪所能承受的最大载荷随各参数变化的规律。

图7 模拟壁面与竖直面存在小倾角示意图

当脚爪上爪刺数量相同时,爪刺的排列密度对脚爪所能承受的最大载荷产生影响的实验步骤如下:先制作6只具有16根爪刺的脚爪,爪刺间隔分别为1、2、…、6 mm;然后在图6的模拟壁面上随机选择5个不同区域,分别测试脚爪抓附墙面所能承受的最大载荷。将实验测试结果平均值进行拟合,得到的曲线如图8所示。

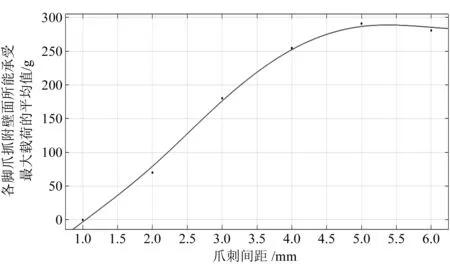
图8 不同爪刺间距脚爪所能承受最大载荷平均值的拟合曲线

从图8中可以看出,在抓附壁面过程中,当爪刺之间刚好相互不影响时,爪刺之间的排列密度取得最优值,此时在单位面积内,抓附在墙面上的爪刺数量最大。同时,在由24目砂纸制作的模拟墙面上,当爪刺之间间隔为5 mm时,脚爪在壁面上的抓附效果最佳,这与1.1中的计算结果基本一致。故本文设计的脚爪采用间隔为5 mm的爪刺排列密度来进行制作。

当爪刺伸出基底的长度不同时,测试脚爪抓附壁面所能承受的最大载荷的变化情况,具体实验过程如下:首先制作4只脚爪,除脚爪上爪刺伸出基底的长度不同外,其余均相同,即脚爪的基底长宽均为14 mm,厚2 mm,且爪刺均间隔3 mm倾斜60°均匀地安装在基底上,而脚爪上爪刺伸出基底的长度分别取0.5、1.0、1.5、2.0 mm;然后在图6的模拟壁面上多次测量脚爪抓附壁面所能承受的最大载荷。同样将实验测试结果的平均值进行拟合,得到的曲线如图9所示。

图9 爪刺伸出基底长度不同时脚爪所能承受最大载荷平均值的拟合曲线

根据图9可知,脚爪伸出基底的最佳长度与脚爪抓附壁面所能承受的最大载荷的变化趋势均与1.2分析的结果接近。故本文以爪刺伸出基底长度为1.2 mm设计脚爪。爬壁机器人脚爪上爪刺的总长L总应为爪刺伸出基底的长度L加上爪刺在基底中长度L基。由于爪刺刚好穿过基底,则L基=δ/sinγ,即爪刺的总长L总=L基+L=δ/sinγ+1.2=3.5 mm,因此爪刺总长取为3.5 mm。

当爪刺尖端直径不同时,测试脚爪抓附壁面所能承受的最大载荷的变化情况,具体实验过程如下:首先制作5只除爪刺尖端直径不同其余均相同的脚爪,即脚爪的基底长宽均为14 mm,厚2 mm,爪刺均间隔3 mm倾斜60°均匀地安装在基底上,脚爪上爪刺尖端直径分别取24、30、36、42、48 μm;然后在图6的模拟壁面上多次测量脚爪抓附壁面所能承受的最大载荷。依然将实验测试结果的平均值进行拟合,得到的曲线如图10所示。

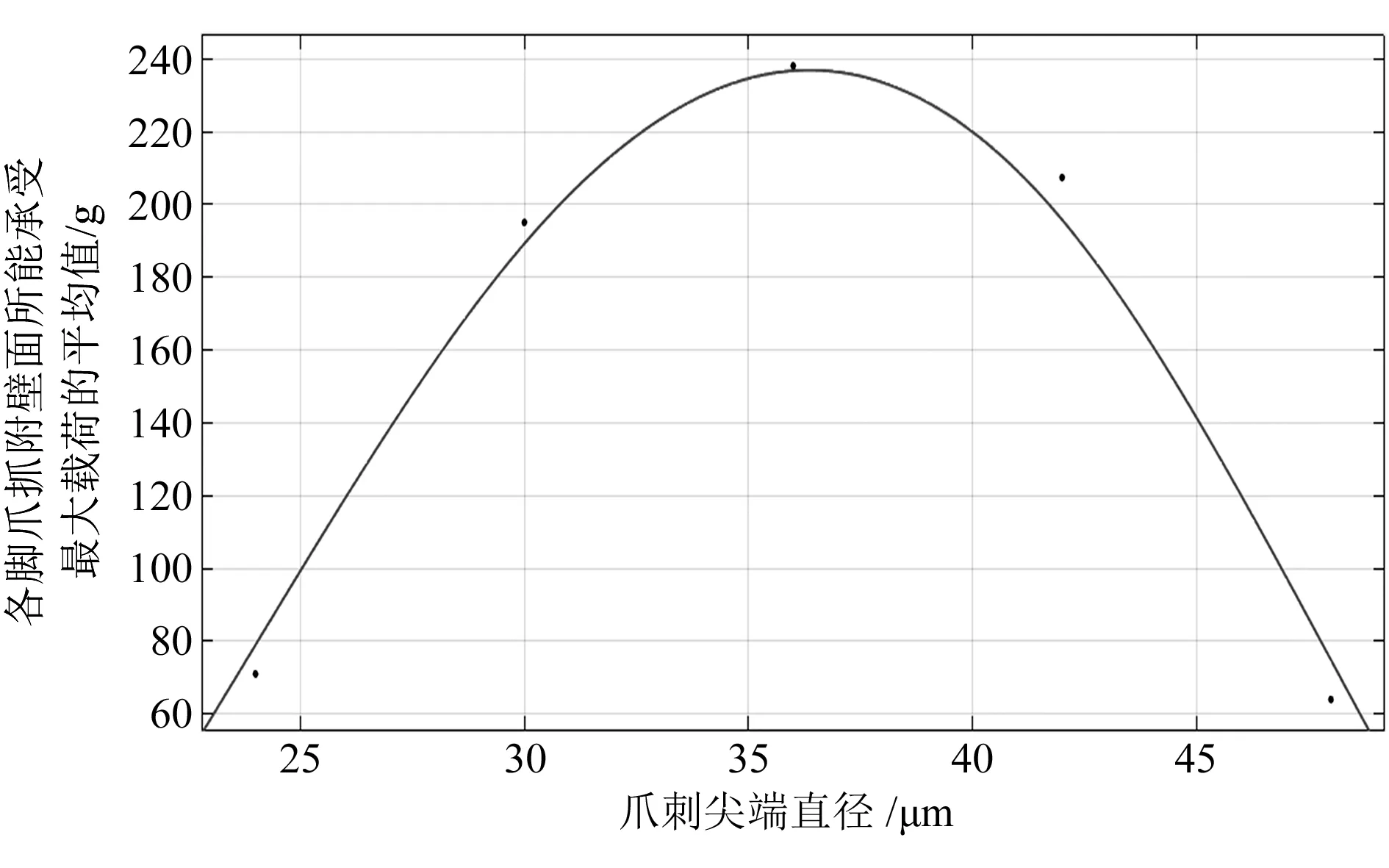
图10 爪刺尖端直径不同的脚爪所能承受最大载荷平均值的拟合曲线

从图10可以看出,爪刺尖端直径的最佳值与脚爪抓附壁面所能承受的最大载荷随着爪刺尖端直径的变化趋势与1.3节分析得到的结果基本相同。经测量,直径为0.30 mm的不锈钢针灸针的尖端直径约为36 μm,根据实验分析结果,同时为了制作方便,本文使用直径为0.30 mm的不锈钢针灸针制作脚爪上的爪刺。

综合以上分析,本文选用直径为0.30 mm的不锈钢针灸针,将其剪成总长度为3.5 mm的爪刺,插到橡胶基底上,以与基底成60°夹角将基底贯穿,最后在基底背面贴一张长、宽和基底相同,厚度为1 mm的硬质纸板,主要目的是防止爪刺从基底背面滑出,并保证爪刺伸出基底部分的长度,爪刺之间间隔为5 mm,每只脚爪上安装32根爪刺,得到的脚爪结构示意图如图11所示,脚爪基底的长度为37 mm、宽度为17 mm。同时,脚爪负重抓附模拟壁面图如图12所示,通过实验,测得每只脚爪抓附模拟壁面所能承受最大载荷超过400 g。

图11 脚爪结构示意图

图12 脚爪负重抓附模拟壁面图

3 结束语

本文通过建立数学模型和实验明确了密集阵爪刺式脚爪部分设计参数的最佳值,完成了爬壁机器人脚爪的设计,此密集阵爪刺式脚爪承载能力超过400 g,改善了目前爬壁机器人脚爪抓附壁面存在的承载能力低、稳定性差等问题。由于时间的限制与思维的局限性,本文对爬壁机器人脚爪的研究还不够完善,仍有很多问题需要进行深入研究,主要包括对描述爬壁机器人脚爪抓附壁面稳定性的参数研究较少。若要拓宽爬壁机器人的应用领域,需进一步改善爬壁机器人脚爪存在的抓附稳定性差的问题,明确描述脚爪抓附壁面稳定性的物理量是下一步工作要解决的问题。