裂纹初始角度对球形压力容器的裂纹应力强度因子与J积分的影响

李有堂,张展涛,杨 佳

(兰州理工大学机电工程学院,甘肃 兰州 730050)

压力容器在生产制造与实际使用过程中,由于制造工艺不稳定、材料本身的相关缺陷和工作中承受温度、载荷等时变因素的影响,使得压力容器壁表面萌生裂纹。随着载荷的不断冲击,导致压力容器中的微小裂纹开始扩展直至贯穿容器表面。

袁浩等[1]发现使用相互作用积分法计算应力强度因子更准确。任中俊等[2]首次运用相互作用积分法计算了混合型裂纹的应力强度因子。刘开泰等[3]发现靠近内壁面侧的裂纹扩展速度更快,靠近外壁面侧的裂纹扩展速度较慢。秦忠宝等[4]发现裂纹尖端最深点的应力强度因子随裂纹倾角的增大而减小。Xie等[5]对有内外裂纹的气缸压力容器进行研究,发现当内外裂纹夹角为0°时,两个裂纹的相互作用会阻碍裂纹扩展。李建[6]发现疲劳寿命与裂纹的尺寸大小呈反比例关系,与单裂纹相比,双裂纹对疲劳寿命的影响更加显著。Perl等[7]通过对球形容器内表面裂纹的研究,发现多裂纹主要影响较厚球形压力容器的疲劳寿命。虽然现有的文献对压力容器裂纹问题进行了大量研究,取得了一定的成果,但这些研究都没有考虑裂纹初始角度对压力容器裂纹尖端应力强度因子与J积分的影响。

本文以含裂纹的球形压力容器为研究对象,使用有限元软件进行数值模拟,通过相互作用积分法对裂纹尖端应力强度因子进行计算,分析裂纹初始角度对裂纹应力强度因子与J积分的影响。

1 理论基础

1.1 相互作用积分理论

通过J积分可以直接求出单一型裂纹的应力强度因子[8],而在实际工况中的疲劳裂纹通常是复合型裂纹,对于复合型的裂纹,通过J积分无法直接求取相应的应力强度因子。为此,提出使用相互作用积分法对此类问题进行求解。

相互作用积分法以J积分为基础,通过建立裂纹尖端的附加场来分离并获取真实场的Ⅰ型和Ⅱ型应力强度因子KⅠ、KⅡ。

Rice提出了J积分:

(1)

其中:

(2)

式中:J为真实裂纹尖端场的J积分,W为应变能密度,T为积分边界上的作用力,u为边界上位移,s为弧长,Г为积分路径,x、y分别为以裂纹尖端为坐标原点平行和垂直于裂纹面的坐标,εij为裂纹尖端的应变,εkl为εij的变化参数,σkl为εij的应力参数。

将真实场和附加场叠加后代入式(1),考虑两种应力状态:

状态1,(σij,εij,uij)为真实应力-变形场的变量。

由此可得:

(3)

各向同性材料的J积分和应力强度因子存在如下关系:

(4)

则

(5)

(6)

(7)

式中:Waux为附加应力-变形场应变能密度,WM为真实场与附加场相互作用下的应变能密度。

通过真实场与附加场的应力强度因子求得相互作用积分M为:

(8)

图1 不同的积分路径

(9)

1.2 球形压力容器裂纹尖端应力强度因子的计算

球形压力容器壁应力示意图如图2所示,容器结构具有轴对称性。图2中,r1为纵线曲率半径,r2为垂直于纵线的环向曲率半径,r1=r2=r,r为球体半径;σ1为纵向应力,σ2为环向应力,σ1=σ2=σ,σ为球形压力容器在承受载荷时球壳承受的应力。

图2 球形压力容器壁应力示意图

根据对称原理,求得球形压力容器在承受内压时球壳受到的应力σ:

(10)

式中:h为容器壁厚度,p为内压力。

根据斜裂纹的双向拉伸理论,线弹性材料中应力、应变和位移满足叠加原理,可得:

(11)

式中:α、β分别为裂纹与σ1、σ2之间的夹角,σ1、σ2分别为纵向与横向所受应力,a为裂纹长度的一半。

(12)

由此可得等效应力强度因子Ke:

(13)

2 球形压力容器的模型建立与网格划分

2.1 几何模型

图3为1/4球形压力容器模型,球体半径r=300 mm,容器壁厚度h=19 mm。初始裂纹位于容器壁中心处,为中心斜裂纹,裂纹初始长度为0.9 mm,裂纹初始角度为45°。由于容器壁厚度远小于球体半径,因此在对裂纹进行数值模拟时,可以将球体压力容器的裂纹问题视为二维平面问题。以上述尺寸参数为依据,建立有限元模型,并通过有限元软件进行分析,材料为Q345,弹性模量E为206 000 MPa,泊松比υ为0.3,屈服强度σs为345 MPa,抗拉强度σb为550 MPa。

图3 1/4球形压力容器模型

2.2 网格划分

球形压力容器模型中包含了中心斜裂纹,如图3所示。在通过有限元软件进行数值模拟的过程中,为了能够得到更加准确的结果,需要对裂纹尖端的网格划分进行加密与精细化处理[9]。

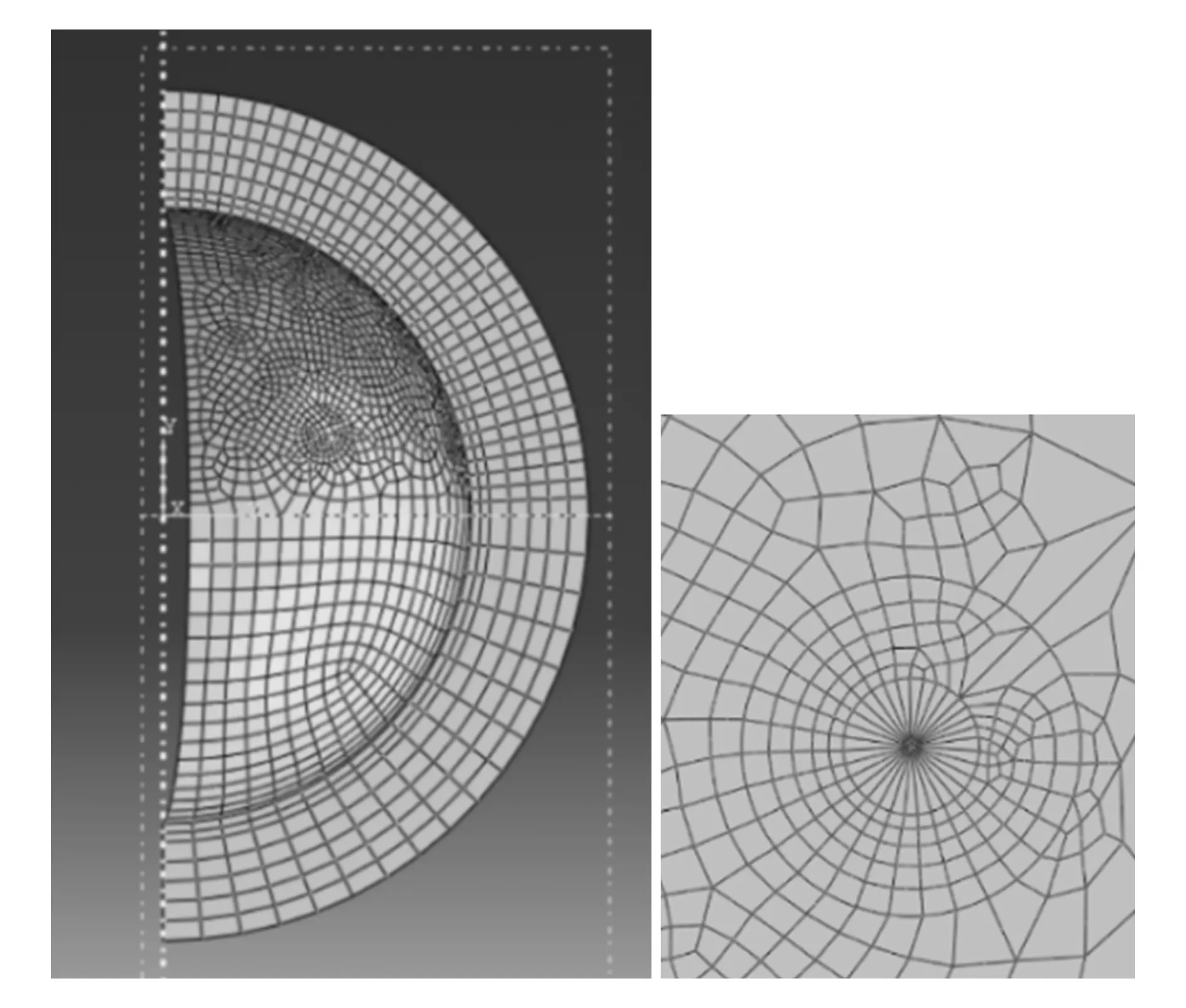
图4 总体网格与裂纹尖端局部网格

按不同的裂纹长度2a、裂纹初始角度β建立相应的模型,并分别施加载荷进行分析求解,得到不同裂纹尺寸比2a/h及β下裂纹尖端的应力强度因子,将在不同条件下计算出的应力强度因子值代入相应公式进行求解。图5为2a/h=0.094 7、β=45°时裂纹尖端处剖面应变、应力云图。

图5 剖面应变、应力云图

3 数值模拟结果与分析

3.1 裂纹初始角度对应力强度因子影响

根据式(12)可知,β是影响应力强度因子的直接参数。

如图6所示,将裂纹与球体法向夹角的互补角定义为裂纹初始角度β。在其余参数不变的条件下,通过改变β的大小,观察应力强度因子的变化情况。为了更清楚地观察β对KⅠ、KⅡ的影响规律,通过相互作用积分法计算出不同条件下裂纹的应力强度因子大小,分别绘制出KⅠ、KⅡ关于β与2a/h的变化曲线,如图7、图8所示。

图6 初始角度示意图

图7 裂纹初始角度对KⅠ的影响

图8 裂纹初始角度对KⅡ的影响

由图7可知,当2a/h不变时,KⅠ随着β的增大而增大;当β不变时,KⅠ随着2a/h的增大而增大。

由图8可知,当β不变时,KⅡ随着2a/h的增大而增大;在不同的β条件下,KⅡ随着2a/h的增大而增大,且变化趋势相同。当β为40°、45°、50°时,KⅡ的变化曲线接近,在该角度范围内KⅡ不受β的影响。

图9 KⅠ、KⅡ与裂纹初始角度

由图9可知,当β增大时,KⅡ先增大后减小,当β=45°时,KⅡ达到最大值。当β<45°时,KⅡ>KⅠ;当β=45°时,KⅠ=KⅡ;当β>45°时,KⅠ>KⅡ。

3.2 裂纹初始角度对J积分与Ke的影响

根据式(4)、(13)可知,KⅠ与KⅡ是影响J积分与等效应力强度因子Ke的直接参数。为了清楚地观察裂纹初始角度β对Ke与J积分的影响规律,通过相互作用积分法计算出不同条件下的应力强度因子值并代入式(4)、(13),分别计算出相应的J积分与Ke,从而分别绘制出β与J积分、Ke的变化曲线,如图10、图11所示。

图10 裂纹初始角度对J积分的影响

图11 裂纹初始角度对Ke的影响

由图10可知,当β增大时,J积分也增大;当β>70°时,J积分的增幅开始减缓。

由图11可知,当β增大时,Ke随之增大,当β>60°时,Ke的变化趋势逐渐平稳。根据图9可知,当β不断增大时,KⅠ不断增大,KⅡ先增大后减小。因此,根据式(13)可知,随着β的不断增大,KⅠ在Ke的变化规律中,逐渐起决定作用。

4 结论

本文基于相互作用积分法求解球形压力容器裂纹尖端的应力强度因子,利用有限元软件分别建立不同裂纹初始角度β与裂纹尺寸2a/h的有限元模型,求得相应的Ⅰ、Ⅱ型应力强度因子KⅠ、KⅡ,代入相应公式求解出J积分与等效应力强度因子Ke,最终得出以下结论:

1)β与2a/h都对压力容器的裂纹应力强度因子存在影响。当β不变时,KⅠ、KⅡ随着2a/h的增大而增大;在不同的β条件下,KⅠ、KⅡ随着2a/h的增大而增大,且变化趋势相同。

2)当β增大时,KⅡ先增大后减小,KⅠ不断增大;当β= 45°时,KⅡ达到最大值,KⅠ=KⅡ。

3)当β增大时,J积分、Ke随之增加,Ke在β大于60°之后逐渐平稳,并且随β的增大,KⅠ在Ke的变化规律中,起决定作用。

4)对相互作用积分法求解的应力强度因子的模拟值与解析值进行对比发现,两者变化趋势基本相同,且最大误差不超过2%,证明了相互作用积分法适用于球形压力容器裂纹尖端应力强度因子的计算。