基于高斯混合模型的汽车车架纵梁故障监测方法研究

张俊妍

(云南国土资源职业学院机电工程学院,云南 昆明 652501)

随着人们生活水平不断提高,汽车出行已经成为常见的交通方式,各大城市频繁出现交通拥堵现象[1]。随着路面车辆的增加,交通事故的发生概率也大大升高。事故在一定程度上来源于驾驶人员的失误,但也有一部分在于车辆存在故障未能及时得到维修所导致,为此应注意车辆的故障检测和故障监测[2]。车架是汽车重要的承载部件之一,遍布整个车体,纵梁就是其中的关键零件之一。在汽车中常见的边梁式车架和中梁式车架均含有纵梁,其承担重要的承载作用,如其存在故障,将会对汽车运行的稳定性造成较大影响,故对其运行状态进行监测、对其故障状态进行识别就显得非常重要。

如胡平[3]针对车辆运行故障监测准确率不高、泛化能力不强的问题,提出了一种故障监测诊断方法。该方法基于卷积神经网络模型,引入贝叶斯网络、支持向量机对其进行改进,以此提升对故障样本的识别能力、收敛速度和泛化能力。最后利用实验进行故障分类,证明所提方法具有可行性,但该方法的分析效果还不够完美,存在故障监测预警效果差的问题。张元星等[4]针对电动汽车充电过程中的监测和预警进行了分析,提出了一种基于电池模型的电动汽车充电故障监测和预警方法。其先通过动力电池模型荷电状态和电池电动势在线估计进行电池荷电状态、电压、温度等参数的调节,从而完成电池充电响应的模拟。在充电过程中采用CAN总线技术来获得充电机与电池的充电信息,通过对比模拟的充电响应信息与电池充电状态信息来完成充电故障的判断。缺点是该方法构建的模型不够完善,存在与实际监测预警效果相差较多的问题。刘文涛等[5]针对车身零部件性能问题,提出基于机器学习进行牵引车车架性能智能评估研究的方法。该方法通过对汽车车架上的零部件进行研究,采用Isight软件搭建批量获取仿真数据流程来获取数据集,然后引入机械学习技术,建立数值响应的预测模型,提升汽车车架性能的预测准确性。该方法可应用于汽车车架故障识别中,但由于其构建的模型不够完善,存在与实际监测预警效果相差较多的问题。

为了解决上述方法中存在的问题,本文针对汽车车架纵梁故障,提出基于高斯混合模型的汽车车架纵梁故障监测方法,希望能够提高车辆车架纵梁故障的识别效率和预警质量,为车辆稳定运行提供基础保障。

1 汽车车架纵梁故障监测数据预处理

在对汽车车架纵梁故障进行监测的过程中,其获取的数据一般分为两种,一种为正常状态数据,另一种为异常状态数据[6]。

为提升汽车车架纵梁故障监测的精准度,需要对获取的数据进行预处理[7],具体操作如下:

1)设置汽车车架纵梁正常状态下获取的数据序列为{Xt},那么{Xt}用方程定义如下:

(1)

式中:α(B)为光滑算子;β(B)为可逆算子;B为延迟算子;ξ为1-B的缩写;α1,α2,…,αq为与α(B)相对应的参数;β1,β2,…,βq为与β(B)相对应的参数;at为正态分布的数据信号序列点[8-9]。

设置{Yt}为采集的异常数据序列,而其在T时刻就会存在缺失值[10],因此假设在t时刻会有持续异常的数据{Yt},可用下述表达式进行定义:

(2)

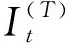
通过式(2)可以发现,异常数据序列{Yt}及t时刻后采集得到的序列{Yt+1}、{Yt+2}都会受到异常数据的影响。

设{Zt}为T时刻存在的持续异常值序列,当其被独立异常值影响时,它的方程表示为:

(3)

根据式(3)可知,独立异常值只对T时刻的序列值产生影响,其余序列值并不会受到干预,所以要将这种类型的值看作独立异常值。

持续异常值及独立异常值对汽车车架纵梁数据序列带来的影响如下所示:

(4)

式中:et为拟合误差,πj为受到残差影响的算子,et+j为(t+j)项的拟合误差,n为j取值的最大值。

对持续异常值和独立异常值的统计量进行计算,以此获取监测的异常值,表示如下:

(5)

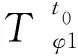
通过上述分析发现,异常数据的不同类型会导致数据在不同时间段内受到不同的影响,所以需要将获取的汽车车架纵梁运行状态数据与式(2)和式(3)相结合,从而实现对初始数据的预处理。

2 故障监测预警方法设计与实现

2.1 T统计故障监测方法的引入

在完成数据预处理后,采用主成分分析法完成数据降维。先对获取的初始样本进行标准化处理,设其标准化的数据集为X,其为一个n×m矩阵,由此可求出其协方差矩阵S为:

(6)

式中:N为数据集X中的样本数目。接下来,对求取的协方差矩阵进行奇异值分解,可得到其特征值为(λ1,λ2,…,λA),其对应的特征向量为(p1,p2,…,pA),其中A为保留主元的个数,其值应该小于样本集中的变量数目。由此,根据其特征向量完成主成分的表达:

Ti=X×P

(7)

式中:Ti为主成分向量集合;P为由特征向量组成的负载矩阵,P=(p1,p2,…,pA)。其单独一个主成分向量ti可表示为:

ti=X×pi

(8)

建立主成分分析模型后,一般采用T统计量来完成运行异常监测,其计算公式如下所示:

(9)

式中:Q为前集合主成分所对应特征值的对角矩阵。当数据样本近似高斯分布时,T统计量视为服从F分布,其控制限TUCL可用式(10)表示:

(10)

式中:α为置信度;Fα(A,N-A)代表置信度为α、自由度为A和(N-A)情况下F分布的临界值。除此之外,还可采用SPE统计量完成故障程度的校验,其控制限ESP,UCL的计算公式如下所示:

(11)

式中:θi为统计自由度;h0为用户定义的常数,用于确定控制限的位置;cα为正态分布(1-α)高位的临界值。

2.2 基于高斯混合模型的T统计故障监测

采用传统T统计方法进行故障监测的过程中容易出现误报的情况,为进一步提升故障监测的效果,本文在此基础上引入高斯混合模型。由于高斯混合模型是一种常见的聚类算法,可通过将事物分解为若干个正态分布曲线,完成事物的精确量化,拟合逼近各种分布,因此本文研究使用置换的方法来估计统计量的分布,进而将基于高斯分布假设的T统计量拓展到非高斯分布的数据集中,并加入滑窗机制以提升数据监测效果。

引入高斯混合模型的T统计方法故障监测步骤如下:

1)先采集故障检测过程中的数据,对初始数据进行标准化后,利用式(6)计算数据的协方差矩阵,然后利用奇异值分解完成其特征向量和特征值的计算,最后基于累积方差贡献率完成主成分个数的确定,得到其负载矩阵及得分矩阵。

2)确定高斯成分个数,利用高斯混合模型对主成分进行求解,得到每个高斯成分的均值uk和协方差σk,其计算公式如下所示。

(12)

(13)

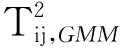
(14)

(15)

式中:tij为第i个高斯成分第j个样本的主成分。

3)利用式(11)求出SPE统计量的控制限。

4)将算得的T统计控制限和SPE统计量控制限与设定阈值进行比较,如只有一个指标超标,即可判断系统异常;如没有指标超标,则可判断其并无故障,以此完成故障监测。

3 实验与分析

为验证基于高斯混合模型的汽车车架纵梁故障监测方法的整体有效性,在主频为 3.60 GHz、内存为 8 GB 的 PC 机上,使用 Python 软件开发环境和 Open CV 开发工具进行仿真实验测试。对某车辆进行研究,在4个纵梁交汇点布置传感器,其布置图如图1所示。

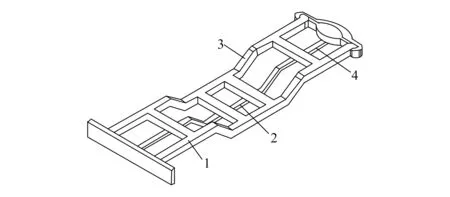
图1 传感器布置图

如图1所示,利用布置的传感器完成车架纵梁运行状态数据的采集,并将其组成数据集。其中,选取数据集中80 000个振动数据作为训练集,10 000个数据作为测试集。测试集及训练集中均具有大量的故障。先对所提方法的应用性能进行检验,获得效果如图2所示。

图2 所提方法检测结果

结合图2(a)、(b)可知,采用本文所提方法可对汽车车架纵梁的运行状态进行科学评估,通过异常数据的筛选完成故障监测。为进一步验证所提方法的性能,选取基于高斯混合模型的汽车车架纵梁故障监测方法(方法1)、铁路机车车辆运行故障监测诊断研究(方法2)、基于机器学习的牵引车车架性能智能评估(方法3)开展对比实验。

1)选取500个车辆纵梁实时数据,利用方法1、方法2和方法3对数据进行检测分析,并将其与真实结果相对比。若测试结果与实际结果相近,说明该方法的故障监测预警效果好;若测试结果与实际结果相差较多,说明该方法的故障监测预警效果差。统计其预警准确率,获得具体测试结果如图3所示。

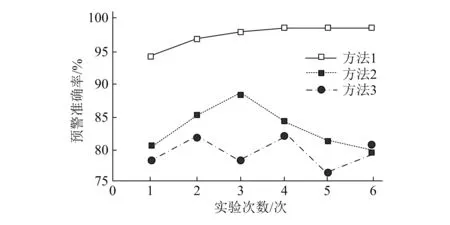
图3 不同方法故障监测预警准确率对比

分析图3中的数据可知,应用方法1在2、3、4、5、6次实验中,检测准确率均超过95%,对故障监测预警的效果较好,而应用方法2和方法3在测试期间的故障监测效果不佳,均低于90%,且其监测稳定性较差,这不仅仅说明方法2与方法3的故障监测误差大,还说明方法2与方法3的故障监测方法还有缺陷,应该加以完善。

2)基于上述实验,为了充分验证所提方法在不同时间段的故障监测预警效果,需要利用方法1、方法2和方法3分别对不同月份的变电站电气设备进行故障监测预警,选取3月、6月、9月及12月4个月份作为研究对象,得到不同月份下的故障监测效果,如图4所示。

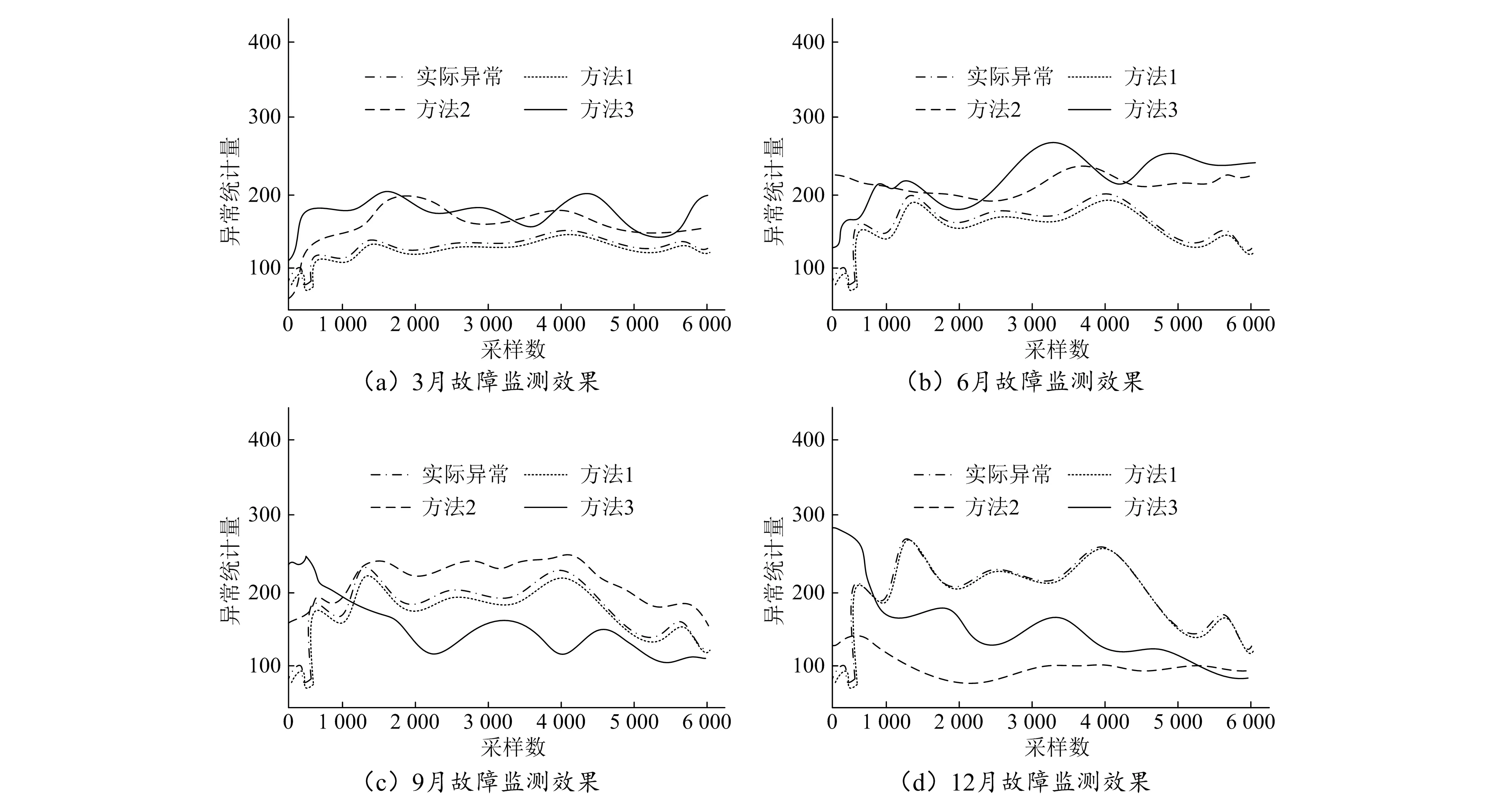
图4 不同月份的故障监测效果对比

根据图4(a)可知,采用方法1进行故障监测预警的准确率较高,其异常数据的统计量与实际异常数据数目大致相符,而方法2和方法3的异常数据统计情况与实际异常情况虽然较为接近,但其应用效果仍然不佳。综合图4(a)、(b)、(c)、(d)可知,方法1监测效果与实际结果更为接近,方法2和方法3在12月的监测均出现较大误差,故方法1的故障预警监测效果更佳。这主要是由于方法1对获取的数据进行了预处理,提升了故障监测准确率。

4 结束语

本文给出的汽车车架纵梁故障监测方法仿真应用效果较好,且不受月份影响,在全年预警过程中均优于对比方法,可为汽车车架纵梁故障监测提供一种新的方法,为后续汽车车架故障检测与维修类系统的设计与研究提供一定技术支持。但是目前的研究工作仅通过简单实例验证方法的可行性,实际应用效果还未得到验证,后续还需要将本文方法应用在实际工作场景中,以真正完成方法应用效果的验证。