基于多层感知机与无网格策略的三维空间声源识别

贺银芝， 杨现晖， 刘永铭， 杨志刚， 庞加斌

（1. 同济大学 汽车学院，上海 201804；2. 同济大学 上海地面交通工具风洞中心，上海 201804；3. 同济大学 上海地面交通工具空气动力与热环境模拟重点实验室，上海 201804）

波束形成作为一种声场可视化技术，常用于声源定位。常用的波束形成算法主要包括传统互谱算法及其增强、解卷积算法等。传统互谱算法原理简单，运算速度快，具有较强的鲁棒性，然而它的主要缺点包括低频时较差的空间分辨率以及由于旁瓣效应造成的较差的动态范围。常用的解卷积算法包括CLEAN［1］、CLEAN-SC［2］、DAMAS［3］等算法，相比于传统互谱算法，有更好的空间分辨率和动态范围。但基于相控麦克风阵列的波束形成算法仍存在两方面不足：一是无法同时满足高效率和高性能；二是在传递矢量未知的复杂流动环境中使用相控麦克风阵列时，由于传递矢量的不确定性，相控麦克风阵列识别精度会很差［4］。

在经典假设（非相干声源、单极子传播、无混响环境、均匀介质）不成立的情况下，机器学习的应用前景广阔。深度学习作为一种特殊的机器学习，通过使用反向传播算法，能够从大量的数据中，找到输入与输出数据间的关系。近年来，随着深度学习与神经网络的发展，很多学者尝试将深度学习应用于声源识别，这些工作大多集中在获取声源的到达方向（direction of arrival，DOA）。最近几年，有一些学者开始使用深度学习方法研究如何确定声源的具体位置与强度。

2018 年，Ma 等［4］构造了七层卷积神经网络，并应用于麦克风阵列声源定位，他们将麦克风阵列采集到的信号所构成的互谱矩阵转换为图像作为输入，将各个网格点上的声源强度作为输出，通过大量的数据训练，发现在一定频率和网格密度情况下，对于多点等强度声源，卷积神经网络能够较为准确地识别声源位置，并且计算速度明显快于DAMAS 算法。但是，由于其网格划分仅为160 mm×160 mm，故结果不切实际。在Ma 等［4］的基础上，宋章辰等［5］构造了相似的卷积神经网络，探讨了空间分辨率与网格间距的比值对神经网络训练精度的影响。

基于网格点的策略限制了神经网络出色的非线性建模能力，也限制了声源识别的空间分辨率，因此本文采用无网格策略。所谓无网格策略即不将声源区域划分成若干网格，可以大大增加声源识别的空间分辨率。Castellini 等［6-7］在2021 年提出一种基于多层感知机的无网格声源定位方法，将互谱矩阵重新排列成一维列向量作为输入，输出是多个声源的位置及强度。文献［8-9］中均使用了一种基于残差网络的声源定位方法，同样基于无网格策略，输入的是传统互谱算法得到的声源分布图，输出的是声源位置及强度，能够定位任意频率的单声源，并且精度高于传统互谱算法，在声源强度方面也有较高精度。

三维空间声源定位在实际应用中具有非常重要的意义，比如对复杂的机械部件、发动机和一些气动声源等噪声源的定位。有两种方法实现三维波束形成：第一种方法是将声源潜在的三维空间划分为多个有一定间距的、平行于麦克风阵列的声平面，然后用二维平面麦克风阵列逐一扫描，寻找声源。这种方法应用简单，对麦克风阵列设备要求不高，缺点是单一平面麦克风阵列在垂直阵列方向上的空间分辨率较差［10-11］。第二种方法是构造三维麦克风阵列。2006 年，Meyer 和Döbler［12］利用GFai公司设计开发的球形麦克风阵列重构了车内声场，球形麦克风阵列后来也被广泛应用于复杂三维物体表面的声源定位。2009年，Maffei 和Bianco［13］在Pininfarina 风洞的顶部和侧壁各安装了一个麦克风阵列，分别由78和66个麦克风组成，结合光学扫描系统测得的车辆几何形状，很好地识别了车辆表面的气动噪声源。2013年，Padois等［14］在风洞两侧安装了4个麦克风阵列，每个阵列由48个麦克风构成，用来识别三维单极子声源和偶极子声源。2014 年，Porteous等［15］在Adelaide大学风洞内利用两个正交麦克风阵列来实现三维声源的定位。2016年，Döbler 等［16］在保时捷风洞用三个麦克风阵列识别了汽车表面的气动噪声源，麦克风阵列分别被布置在车辆的顶部和左右两侧。2018年，Ocker和Paul［17］在保时捷风洞中用三个麦克风阵列结合激光扫描系统进行了类似的工作。

本文在Castellini 等［6-7］工作的基础上，使用多层感知机神经网络，并基于无网格策略，将二维平面声源定位拓展到三维空间声源定位。针对等强度双声源的位置和强度进行了预测，并与波束形成算法的结果进行了对比，探讨训练数据数量以及声源频率对多层感知机、波束形成算法的影响。

1 算法原理

1.1 传统互谱算法

对于xs处一个强度为q的声源，第i个麦克风上测到的声压为

其中g(xi，xs)是xs处的声源到xi处麦克风的传递矢量，对于无来流时的单极子声源，其传递矢量为

式中：ω是角频率； R=xi-xs为声源到麦克风之间的距离矢量为单极子声源在流体中的传播时间，其中c为声速。对各个麦克风测到的声压信号进行加权，在声源区域任意一点xt上计算到的声压为

式中：p 是所有麦克风测到的声压；H 是共轭转置；h(xt)称为导向矢量［18］，本文选用

式中：g 是传递矢量；N 是麦克风数量。将加权后的声压信号做自功率谱计：

式中：E是期望算子；“*”是复共轭；C是互谱矩阵。

导向矢量公式（4）能够准确地计算声源位置，但是会错误计算声源强度，因此需要幅值校正。因为使用该导向矢量公式时，对二维平面没有问题，但对于三维空间来说，波束形成算法会引入空间相关的“阵列增益”，这个“阵列增益”将放大靠近麦克风阵列中心的信号，缩小远离麦克风阵列中心的信号。这个增益理论上可以用式（5）计算出来的声源强度除以一个修正系数rcor来消除，则正确的声源强度Btrue为

结合Sarradj 等［10］的工作，可推导出对于单极子声源，其修正系数为

1.2 多层感知机神经网络

本文提出的神经网络模型是针对回归的多层感知机（MLP）方法，给定一组输入-输出连续变量，该模型的任务是在给定新的统计独立的输入数据的情况下预测新的连续输出。多层感知机是一种特定的前馈人工神经网络（ANNs），它有一个输入层，一个或多个隐藏层和一个输出层，可以根据任务（即分类或回归）进行模型构建，本文提出的模型是基于六层隐藏层的MLP 架构，具有整流线性单元（ReLU）和线性激活函数。而且网络参数数量要满足以下条件4×S×M≫参数数量［6-7］，例如在本文中200 万数据（M）、2个点生源（S），参数数量为1 296满足此条件。

将互谱矩阵展开成一维向量作为输入［6-7］，将声源的三维坐标以及强度作为输出，互谱矩阵的大小取决于麦克风数量。本文所用36 通道麦克风分布在XZ平面上，如图 1a所示。潜在声源区域中心（0，0，1）到麦克风阵列所在平面的距离是1 m，潜在声源区域是一个0.5 m×0.5 m×0.5 m 的三维空间，声源在潜在声源区域中随机分布，所用的双点等强度声源的位置和强度随机生成，声源强度范围为80～100 dB，如图1b所示。

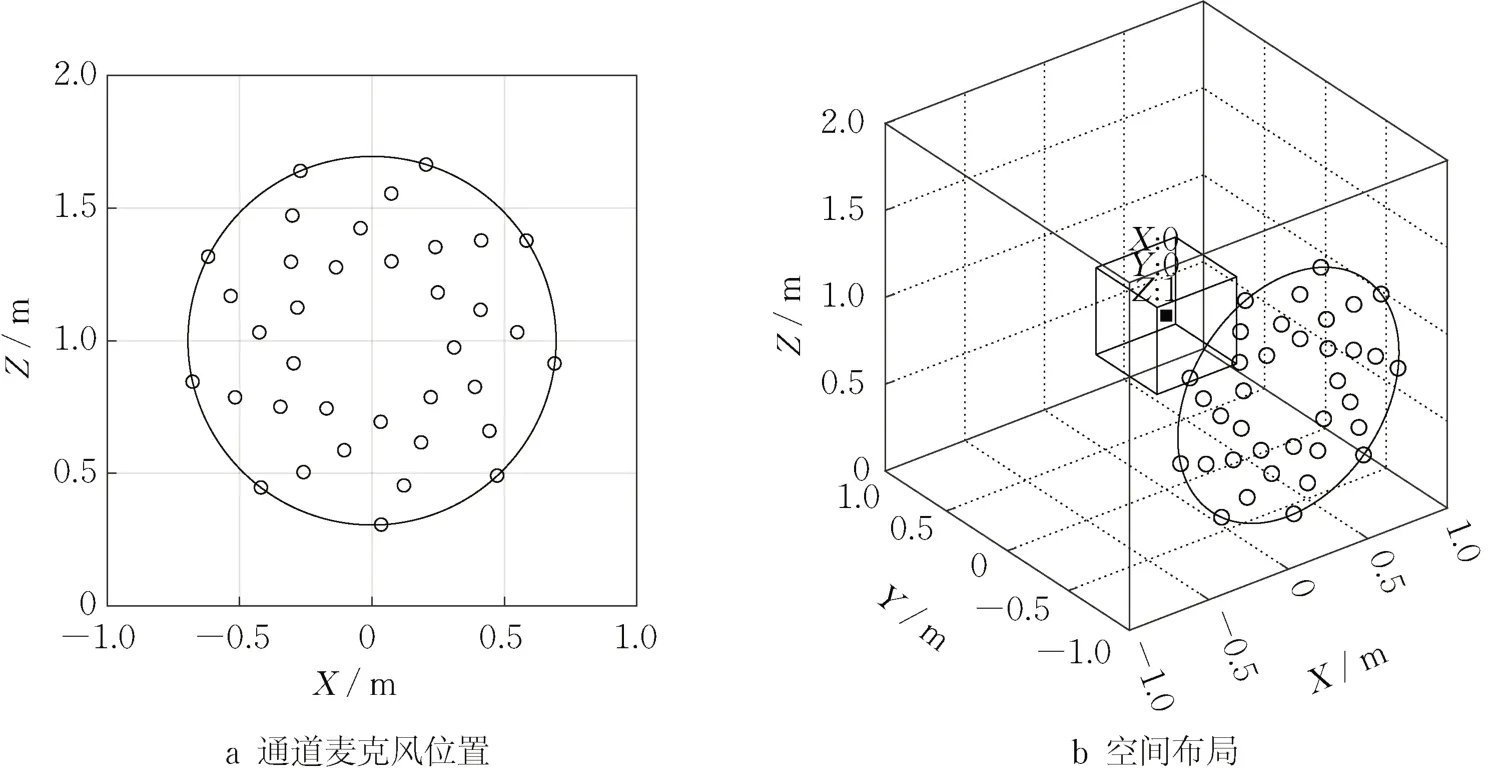
图1 36通道麦克风的位置与声源区域和麦克风阵列的空间布局Fig. 1 Location of 36-channel microphone with sound source area and spatial layout of microphone array

为了便于训练，将声源位置和强度分开，分别建立两个模型，一个输出预测声源的位置，另一个输出预测声源的强度。模型的参数和结构见表1和表2，可训练参数分别为285 633和285 591。对于三维空间的声源定位比二维平面多了一个坐标值，在预测声源位置时，输出层增加了一个神经元。

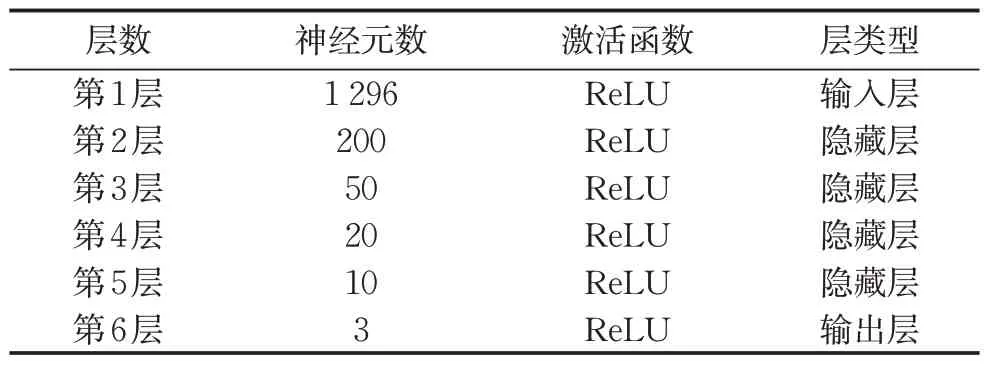
表1 多层感知机神经网络模型结构参数 （用于声源位置预测）Tab. 1 Infrastructure parameters of multi-layer perceptron neural network model (for sound source localization prediction)

表2 多层感知机神经网络模型结构参数（用于声源强度预测）Tab. 2 Infrastructure parameters of multi-layer perceptron neural network model (for sound source intensity prediction)

对于神经网络来说，收集大量数据用于模型的训练、验证和最终测试是很重要的。本文通过随机仿真生成的方法获得大量数据：加载麦克风阵列中各麦克风的位置；随机生成大量不同位置不同强度的双点等强度声源；根据式（5）生成所采用麦克风阵列的互谱矩阵。在训练过程中，将生成的数据集按8：1：1划分，分别作为训练数据、验证数据和测试数据。

多层感知机预测声源具体的位置和强度，属于一个回归问题，因此选用均方误差作为损失函数，来衡量预测值和真实值之间的误差：

式中：L为模型预测的声源位置数量或强度数量为真实的声源位置或强度；xi为预测的声源位置或强度。在神经网络训练过程中，通过调整权重参数和偏置来降低损失函数。这里选用Adam优化器来更新权重参数和偏置。学习率设为0.001，批处理参数（batch size）设为5 000，迭代100 步。使用的电脑CPU速度为2.10 GHz，显卡型号为1070ti。

2 结果分析

2.1 多层感知机与波束形成算法仿真性能对比

选用5 000 Hz时1万组随机分布的声源作为测试对象，选取0.005 m的网格长度，得到的声源位置误差和强度误差如图2所示。

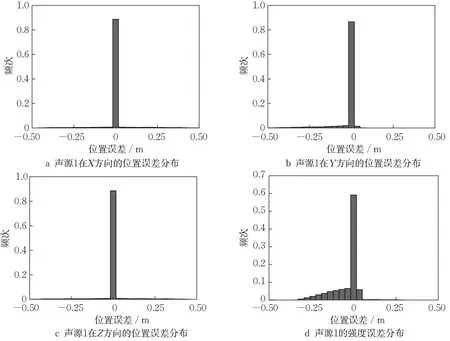
图2 基于传统互谱算法得到的声源1的位置误差与强度误差分布（5 000 Hz）Fig. 2 Position error and intensity error distribution of sound source 1 based on conventional cross-spectrum algorithm (5 000 Hz)

图2中纵轴的频次等于频数除以总数。可以看出，声源1在X、Z方向的位置误差近似关于0对称，主要集中在0附近，但是还存在小部分极大的误差（远大于网格长度，称这部分误差为极端误差）。Y方向的误差，大部分分布在0附近，但是极端误差却全部集中在负半轴，这是因为对于三维波束形成，在使用了导向矢量后，会放大靠近麦克风阵列的信号，缩小远离麦克风阵列的信号；对于等强度双点声源，当两声源近似垂直于XZ平面时，只能精确计算靠近麦克风阵列的那个声源的位置与强度，并且由于靠近麦克风阵列的信号被放大，故会在靠近麦克风阵列的某个位置出现第二个极大值。三维波束形成算法会将其识别成第二个声源，因此计算得到的Y值减小，Y方向出现位置误差，并且为负值。至于声源强度，靠近麦克风阵列的那个声源强度经过幅值校正后，强度准确，但是远离阵列的那个声源强度会被减弱，并且会在靠近麦克风阵列附近产生一个“伪声源”，强度低于第二个声源强度。

相比于传统互谱算法，基于解卷积的CLEAN-SC算法性能更好，且不受阵列点传播函数的影响。图3所示为使用CLEAN-SC得到的位置误差以及强度误差分布图。从图3可看出，CLEAN-SC得到的位置误差远小于传统互谱算法，在X、Z方向上的误差主要集中在一个网格长度范围内，在Y方向上的误差主要集中在三个网格长度范围内，表明平面麦克风阵列在垂直阵列方向上的位置误差要大一些。但是强度误差方面，CLEAN-SC极端误差的值和出现的频次都要更大一些。

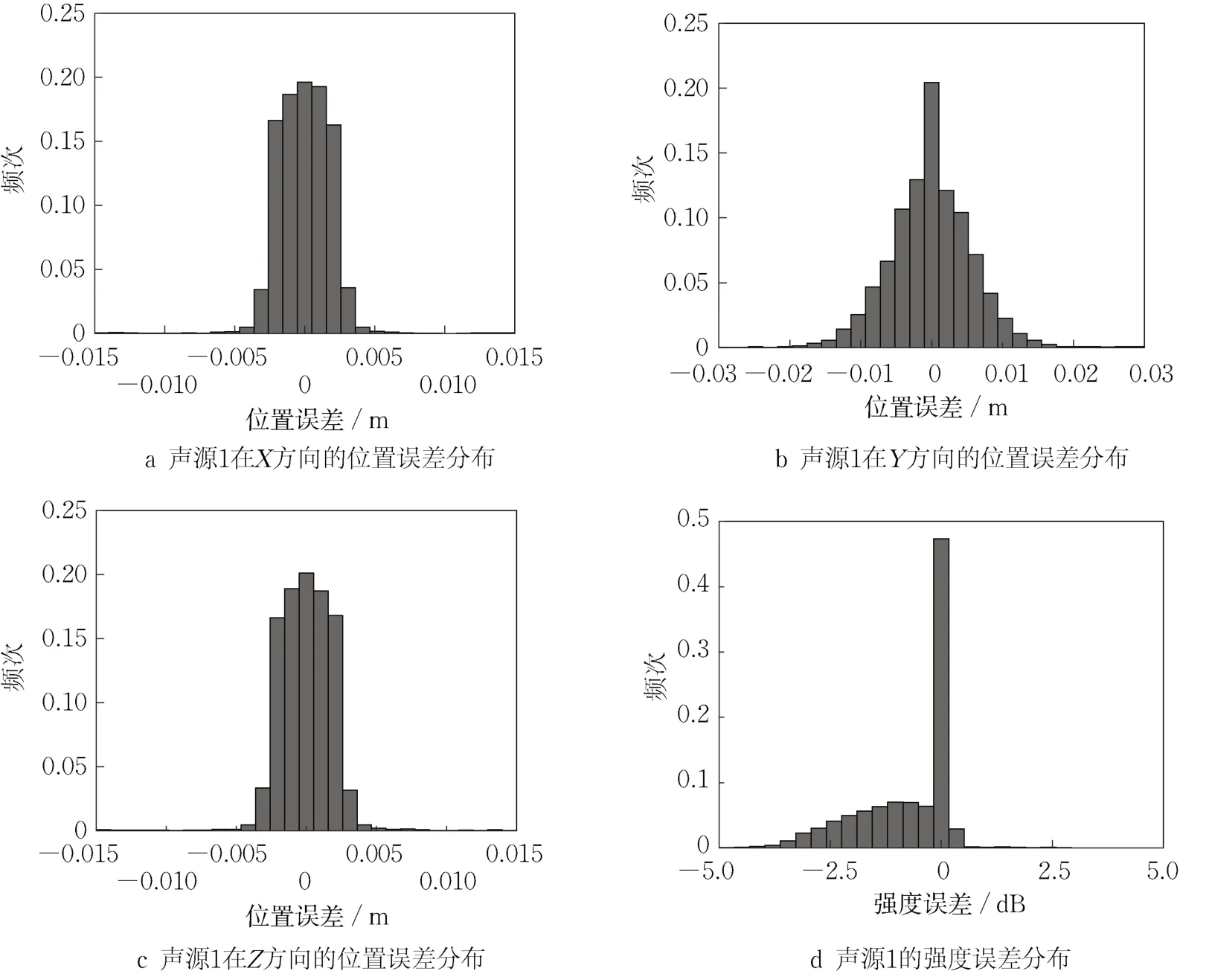
图3 网格边长为0.005 m得到的双声源位置误差与强度误差分布（5 000 Hz）Fig. 3 Position error and intensity error distribution of dual sound sources with a mesh side length of 0.005 m (5 000 Hz)

对随机分布的等强度双点声源，保持频率为5 000 Hz，用160万训练数据去训练多层感知机，得到的损失曲线如图4所示。可以看出，声源位置和强度的均方误差很快就变得很小且趋于不变，说明多层感知机收敛很快。图5为识别的声源位置误差和强度误差（多层感知机，160万训练数据），发现基于多层感知机得到的双点声源三个方向上的位置误差均优于基于传统互谱算法的结果（图2），并且消除了极端误差，在Y方向上的空间分辨率也很好。值得说明的是，基于多层感知机的强度误差较小，优于各种波束形成算法。

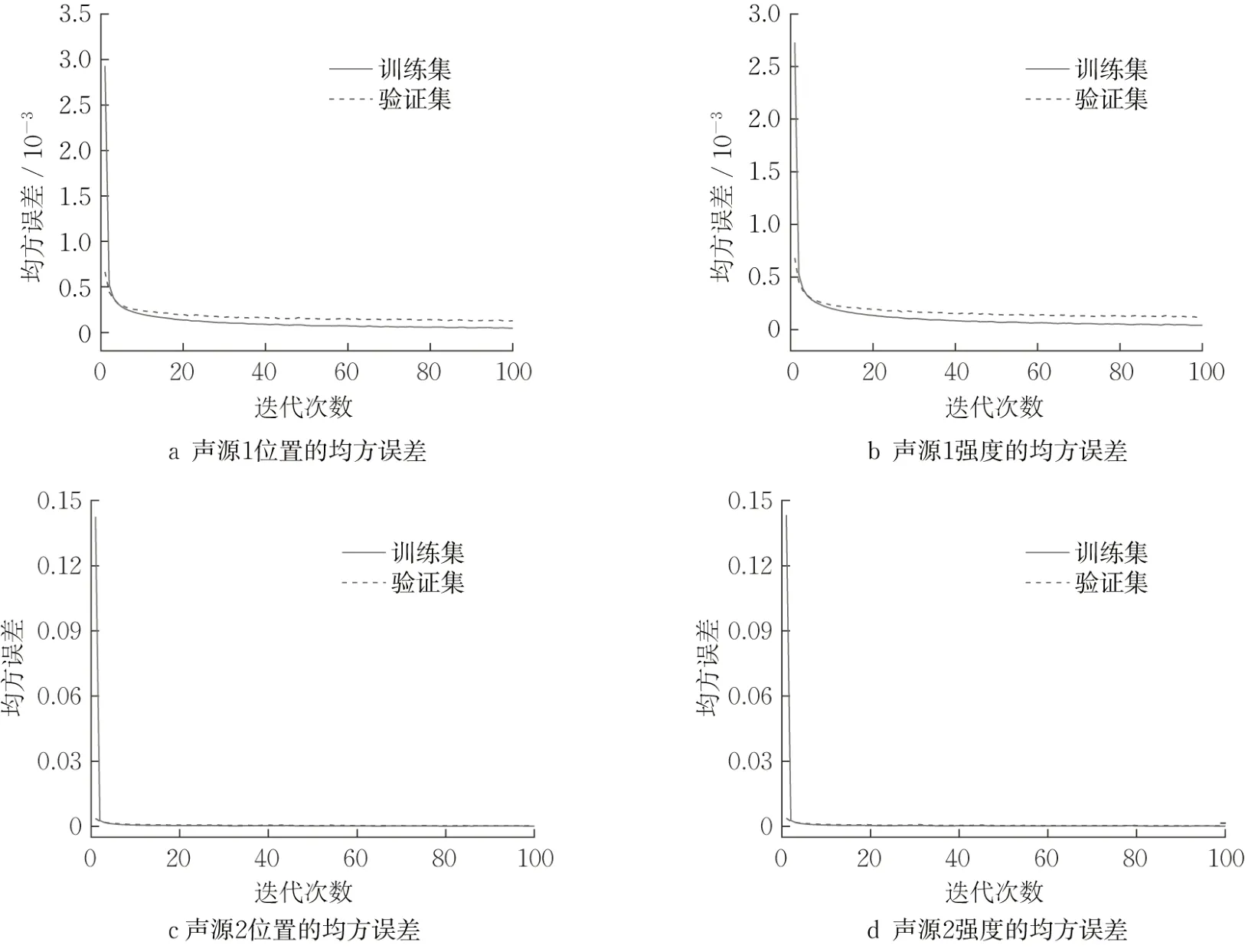
图4 基于160万训练数据得到的双声源的位置与强度损失曲线（5 000 Hz）Fig. 4 Position and intensity loss curves of dual sound sources based on a training data of 1.6 million (5 000 Hz)

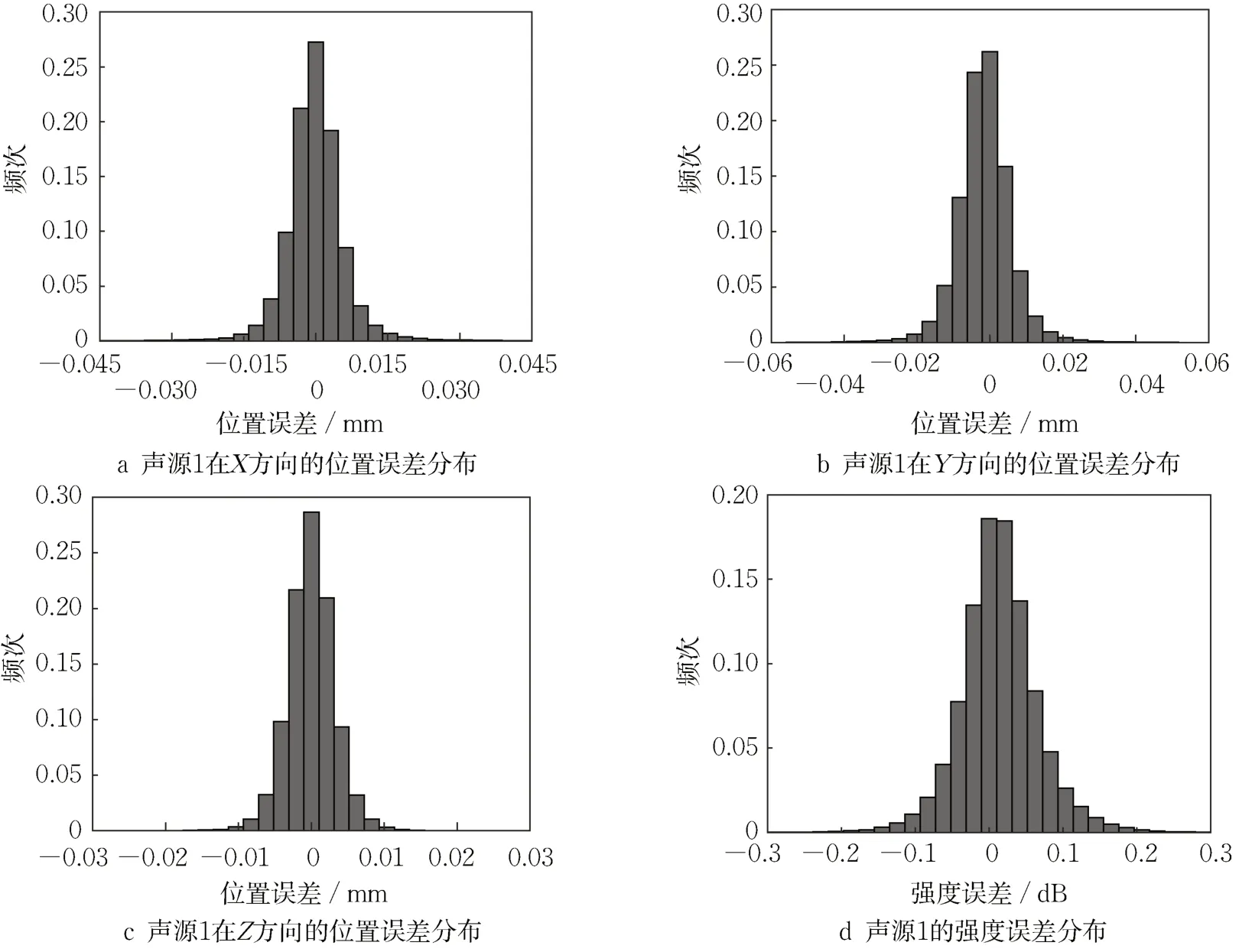
图5 基于160万训练数据得到的声源1的位置误差与强度误差分布（5 000 Hz）Fig. 5 Position error and intensity error distribution of sound source 1 based on training data of 1.6 million(5 000 Hz)

2.2 训练数据量的影响

对于随机分布的等强度双点单极子声源，保持频率为5 000 Hz，分别用40万、80万、160万的数据训练多层感知机，发现随着训练数据的增大，多层感知机逐渐充分学习到数据中隐藏的规律，位置误差和强度误差不断减小。

2.3 频率的影响

在声源定位过程中，声源频率是最重要的考虑因素之一。下面探讨声源频率对多层感知机与波束形成算法的影响。图6、图7分别为2 000、8 000 Hz频率下，基于CLEAN算法得到的声源1的位置误差及强度误差（网格边长0.005 m）。可以发现随着声源频率增大，声源位置的极端误差减小，强度误差也有所改善。图8、图9分别为2 000、8 000 Hz频率下，基于160万训练数据得到的点声源1的位置误差与强度误差。

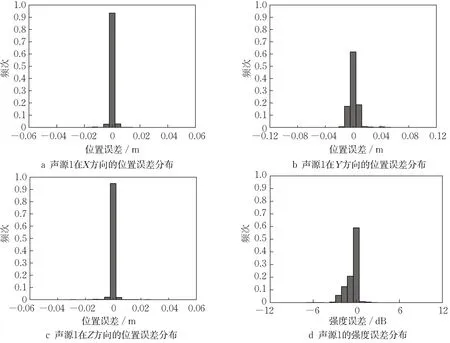
图6 基于CLEAN得到的声源1的位置误差与强度误差分布（2 000 Hz）Fig. 6 Position error and intensity error distribution of sound source 1 based on CLEAN (2 000 Hz)

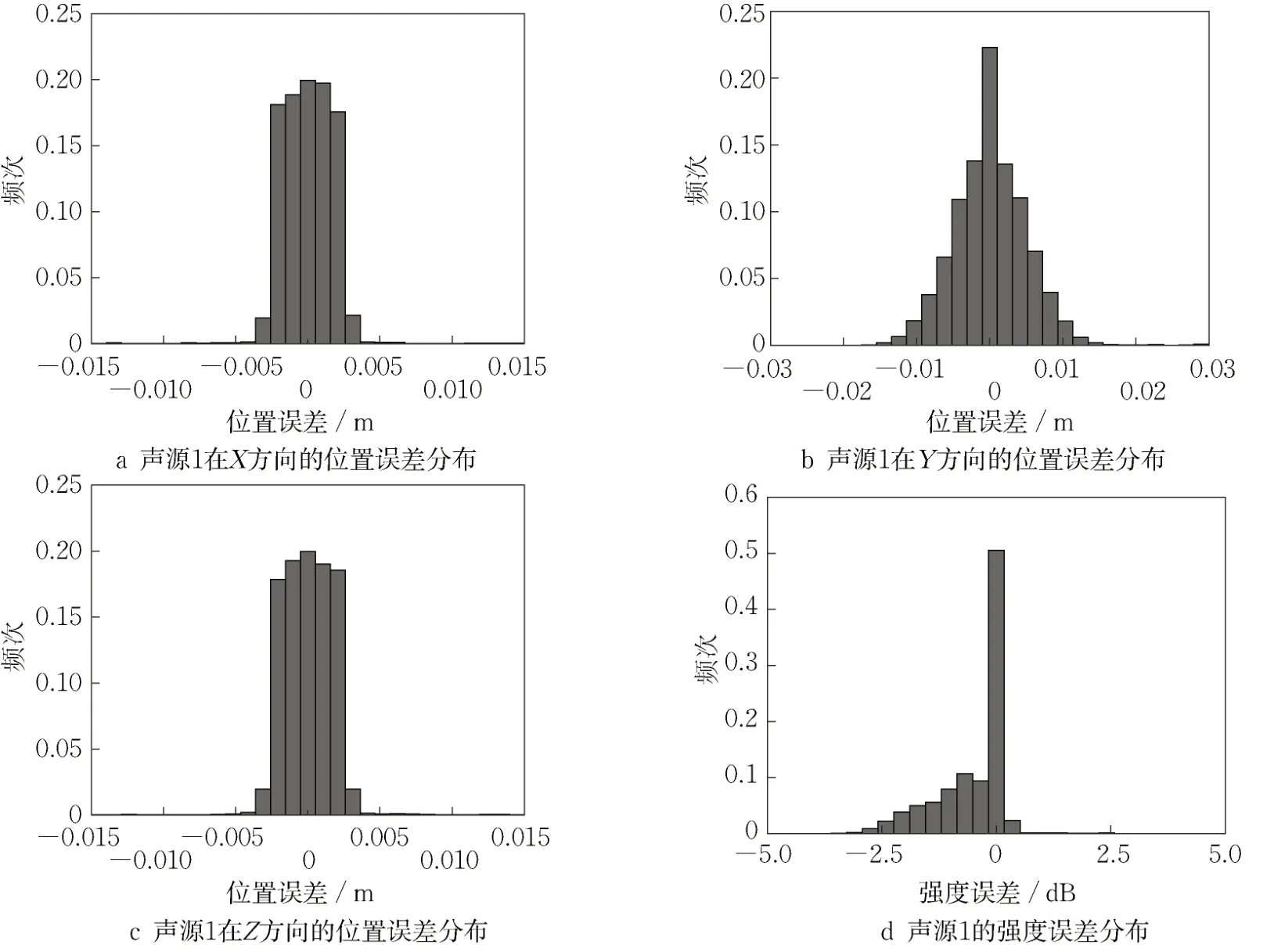
图7 基于CLEAN得到的声源1的位置误差与强度误差分布（8 000 Hz）Fig. 7 Position error and intensity error distribution of sound source 1 based on CLEAN (8 000 Hz)

图8 基于160万训练数据得到的声源1的位置误差与强度误差分布（2 000 Hz）Fig. 8 Position error and intensity error distribution of sound source 1 based on training data of 1.6 million

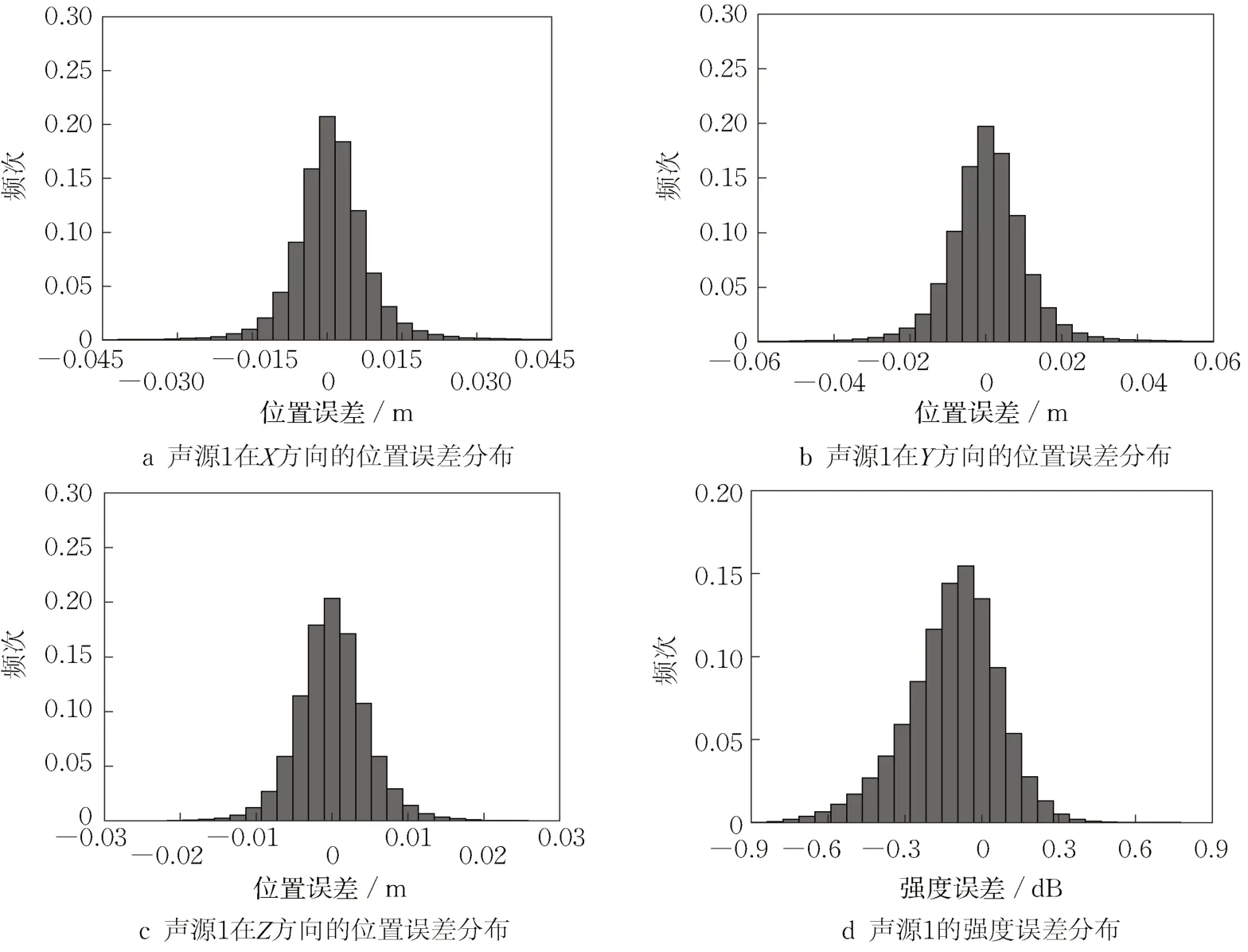
图9 基于160万训练数据得到的声源1的位置误差与强度误差分布（8 000 Hz）Fig. 9 Position error and intensity error distribution of sound source 1 based on training data of 1.6 million(8 000 Hz)

可以发现，随着声源频率的增大，位置误差和强度误差略有增大。相比基于CLEAN算法计算的声源位置误差及强度误差，在低频时，多层感知机的位置误差更小；高频时，多层感知机的位置误差偏大。声源强度方面，多层感知机的强度误差远小于波束形成算法得到的强度误差。

3 结论

多层感知机算法与传统互谱算法、解卷积算法等波束形成算法有着明显区别。首先，多层感知机算法不需要预先得到声传播方程，即传递矢量，而传递矢量是波束形成算法的先决条件；其二是多层感知机算法甚至不需要预先知道麦克风在阵列中的位置，这也是波束形成算法的先决条件。第一个区别使得多层感知机算法有一个巨大优势，即可以在很多复杂场景中使用。在这些场景中，因传递矢量未知而无法使用波束形成算法。第二个区别使得多层感知机算法具有另一个优势，即可以避免麦克风在安装过程中由位置偏差引起的误差。但是，这些优势的前提是多层感知机算法可以准确地从互谱矩阵中计算到声源位置以及强度。

本文使用了具有Tensorflow 后端的keras 框架来搭建多层感知机神经网络，通过Matlab 产生了大量仿真数据。通过训练后，对双点等强度声源的位置以及强度进行了预测，并与波束形成算法进行了对比，得到以下主要结论：

（1） 多层感知机训练过程需要几个甚至十几个小时，训练数据越多所需要的时间越久，消耗的计算资源越多，但是训练完成后的计算速度非常快。如果有大量数据需要处理，可以考虑使用多层感知机。随着训练数据的增加，多层感知机逐渐充分学习到数据中隐藏的规律，位置误差和强度误差均在减小。

（2） 相较于传统互谱算法，CLEAN等解卷积算法计算到的双点声源的位置误差大大减少了，但是强度方面，极端误差的值和出现的频次都要更大一些。波束形成算法强度误差较大，且主要集中在负半轴。多层感知机采用无网格策略，位置误差与强度误差与网格间距无关。

（3） 多层感知机在三个方向的位置误差、特别是Y 方向的位置误差，远小于传统互谱算法的位置误差，但是性能不及CLEAN算法。在强度方面，多层感知机的性能好于各种波束形成算法。

（4） 随着声源频率的增大，波束形成算法计算到的声源位置的极端误差在减小，强度误差也有所改善；而多层感知机预测的位置误差和强度误差略有增大。多层感知机在低频时性能优于波束形成算法，可用来弥补波束形成算法在低频时空间分辨率性能不佳的局限性。

作者贡献声明：

贺银芝：思路设计、文章撰写及修改。

杨现晖：数据处理及初稿撰写。

刘永铭：文献查阅及图表绘制。

杨志刚：提出修改建议。

庞加斌：提出修改建议。