轨道车辆运行平稳性评价算法一致性分析

张展飞， 周劲松， 孙文静， 宫 岛， 王腾飞

（同济大学 铁道与城市轨道交通研究院，上海 201804）

由于轨道不平顺与轮对失圆等激励的存在，轨道车辆在运行时总会伴随着振动，导致诸如结构疲劳、噪声与轮轨异常磨耗等问题［1-2］。对于客运列车而言，基于车体加速度是评价车辆运行平稳性或人体振动舒适性的主要方法［3-6］，考虑到人体对不同频率振动的敏感程度，对实测加速度进行频域加权后获得［7］，其中ISO 2631-1［8］采用时域加速度的计权均方根评价人体振动舒适性，对采样时间未有明确要求。在此基础上，国际铁路联盟提出了UIC 513 标准［9］，采用三向计权加速度均方根进行评定，并且规定每段数据采样时间为5 s，同时提出了以50 %或95 %的置信点作为最终评价值。Helberg 与Sperling 在进行了大量试验后提出了Sperling 运行平稳性指标算法［10-11］，该算法忽略了纵向振动，分别计算与评价横向与垂向的平稳性指标，在我国广泛应用［12-13］。该指标可通过时域与频域计算，在算法上又分为均方法与立方法［14］，Deng［15］通过仿真数据分析得到均方频域算法与均方时域算法是等效的，而立方频域算法在采样时间变化时，得到的评价指标结果不同。Sperling 运行平稳性指标的均方时域算法或均方频域算法应用较少，而我国轨道车辆动力学试验标准GB/T 5599［12-13］目前采用的正是立方频域算法。在旧标准GB/T 5599—1985 中，规定采样时间为18～20 s，而在2020 年7 月生效的新标准GB/T 5599—2019中，为了与UIC513标准采样时间相同等原因，将采样时间缩短为5 s。近期研究表明根据运行平稳性算法，随着车辆振动采样时间越短，计算出的指标更大。姜威等［16］采用两个版本标准计算了相同加速度的平稳性指标，发现新标准得到的指标峰值与均值均比1985 版本大。戴源廷等［17］使用GB/T 5599 标准评价非稳态冲击，结果表明采用2 s计算的指标整体上远高于采用20 s计算的指标结果。戴焕云［18］分析了GB/T 5599 标准与原始Sperling算法中加速度加权曲线的差异，发现平稳性指标不能由加权加速度直接换算，但并未涉及采样时间的影响。在GB/ T 5599—2019 这一新标准颁布后，由于采样时间减小而引起平稳性指标增大的现象引起关注。依据GB/T 14849—2005［19］标准要求，地铁车辆型式试验的运行平稳性指标应低于2.5，同样列车振动数据依据1985 版本标准评价为合格，然而根据2019 标准要求，则难以达标。Jiang［20］将ISO2631-1、UIC513 以及GB/T 5599 评价方法进行分析比较，但并未分析采样时间导致平稳性指标差异性的机理。

本文基于某地铁车辆振动测试结果，对比国内外各种振动平稳性与舒适性评价指标算法与判定标准，基于信号频谱转换的时频能量对应性原理分析立方频域算法关于采样时间的不一致性的产生机理，并提出基于统一频率分辨率的等效运行平稳性指标修正算法，建立整车仿真模型计算车体振动加速度，验证一致性修正平稳性算法的有效性。

1 车辆平稳性指标测试评价方法

1.1 轨道车辆平稳性测试评价算法对比

如上节所述，轨道车辆振动舒适性可采用ISO 2631-1［8］人体振动舒适性评价指标算法来进行评价，其计算公式如式（1）所示：

式中：awx、awy、awz分别为纵向、横向、垂向的加权加速度均方根值；kx、ky、kz分别为三个方向的加权系数，评价站立舒适度时均为1。

而UIC 513 标准［9］中的乘坐舒适性指标算法的计算公式，如式（2）所示：

我国GB/T 5599 标准［12-13］中规定的Sperling 指标计算方法为

式中： fi为频率，Hz；ai为fi频率处的加速度幅值，m·s-2；F（ fi）为频率fi的加权函数。

将式（1）、式（2）与式（3）比较可知，ISO2631-1与UIC513 标准计算时采用的是时域振动加速度的平方项，称为均方时域算法，而GB/T 5599标准计算采用的是其频域立方项，称为立方频域算法。对比分析上述轨道车辆运行平稳性与舒适性指标的频率加权函数［8-9，12-13］，其中GB/T 5599 加权函数定义为与其余两指标相似的对于每个ai的加权函数，为(F(fi)/fi)1/3，结果如图1所示。

图1 各平稳性算法的频域加权函数Fig. 1 Weighting function of ride quality algorithms

由于上述车辆振动舒适性与平稳性评价判定标准也不相同，具体如表1所示，因此无法根据加权曲线在同一频率处的值对比三种算法，但仍可分析三种算法的频率敏感性。由图可见，三种评价指标的频域加权曲线各不相同，针对横向振动，ISO2631-1和UIC 513主要考虑1 Hz附近的低频振动，GB/T 5599的加权函数峰值则在较高频的5.4 Hz；针对垂向振动，三种的加权峰值相近，均为6 Hz左右，但ISO2631-1和UIC 513在峰值频率之后的加权系数要大于GB/T 5599，而后者对于0.5～6 Hz间频段的加权系数明显大于前者。

表1 各平稳性与舒适性算法的评价判定标准Tab. 1 Evaluation criteria of ride quality algorithms

1.2 基于实测数据的各算法指标分析

对某地铁车辆进行运行平稳性测试，测试时据GB/T 5599标准要求，将加速度传感器安置于车辆前、后转向架上方偏移车体横向中心线1 m处地板上。传感器量程为5g，采样频率设置为2 560 Hz，以车辆运行在4个站台间不同方向的车体振动测试为例，在运行时车体的垂向与横向振动加速度较大，纵向振动加速度较小，因而运行平稳性指标针对横向与垂向进行评价。

基于上述三个典型区间的实测加速度数据，依据标准分别计算各项平稳性与舒适性指标，如图2所示，计算分析区间内各指标平均值和最大值统计分别如表2所示。其中GB/T 5599依据标准分别采用采样时间5 s和20 s进行分析，ISO 2631-1和UIC 513标准亦采用同样的两种采样时间作为对比。

表2 车辆平稳性指标分析结果平均值比较Tab. 2 Comparison of mean value of ride quality indexes

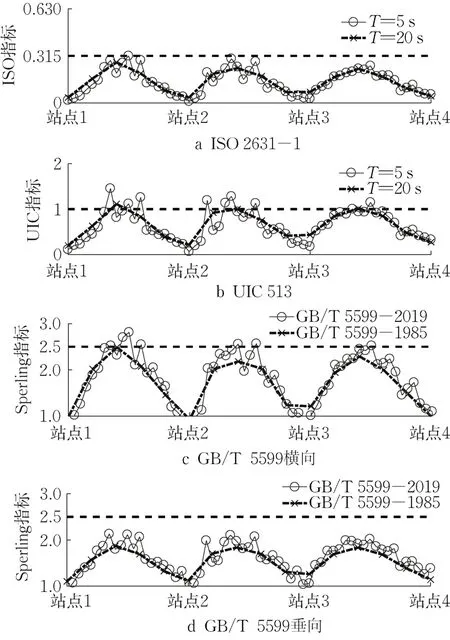
图2 车辆平稳性指标分析结果比较Fig. 2 Comparison of ride quality indexes

由图2可知，以ISO 2631-1标准进行平稳性评估时，所有指标均为最优级别，以UIC 513指标进行评估时，结果为好的舒适性，但是依据GB/T5599标准的1985版本与2019版本进行评估时，则出现了不同的结果。GB/T 5599—2019标准的全程指标计算结果平均高于其1985标准，在1985标准体系下，车辆运行平稳性全程为优，但在新标准体系下，车辆运行至区间中部时横向平稳性仅为良，甚至出现超过2.75的评价结果，此时已超过GB14849—2006标准对地铁车辆的2.5限值要求。

由表2可知，采样时间为5 s时，ISO 2631-1和UIC 513虽指标离散程度更大，但仍是围绕采样时间为20 s的指标曲线波动，指标平均值保持稳定。考虑到轨道条件的随机性，较短采样时间算得的指标具有更强的离散性是正常的。而GB/T 5599分析中，更短的采样时间除指标离散程度不同外，还导致了指标整体偏大不合理现象，平稳性指标用于评价车体振动强度，应与采样时间无关。针对该新旧指标关于采样时间的结果不一致现象，下章将对不一致性的产生机理进行探究，并在第3章进一步提出相应的修正算法以解决该问题。

2 平稳性指标算法关于采样时间差异性分析

2.1 采样时间对运行平稳性指标影响

首先，建立轨道车辆动力学模型，通过仿真得到平稳的时域加速度数据用于平稳性指标分析，分别选取2.5～25 s 作为不同的采样时间分析段，图3a、图3b与图3c所示分别为车体振动加速度时域结果、不同采样时间下的车体横向振动加速度频谱与功率谱密度。

图3 车体振动加速度频域分析结果Fig. 3 Spectrum analysis of carbody acceleration

由图3 可见，不同采样时间下相应的采样间隔频率也不同，其频谱图幅值随着采样时间与采样间隔频率的变化而变化，而功率谱密度函数代表车辆的振动能量，保持不变。

基于图3 中所示的数据，分别计算不同平稳性指标与采样时间的关系，其中各Sperling运行平稳性指标取横向结果，如图4所示。

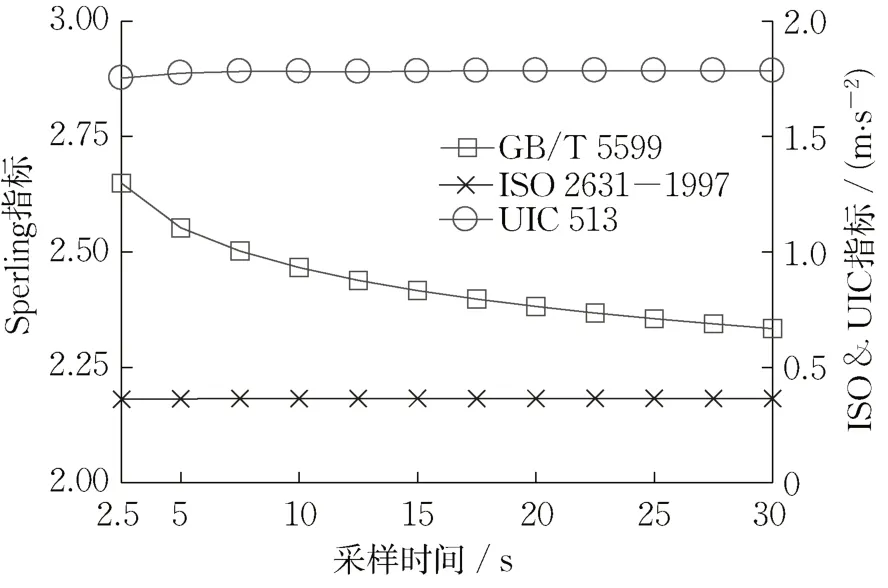
图4 不同采样时间下的各评价指标比较Fig. 4 Comparison of ride quality indexes of different sampling times

由图4 可知，ISO 指标、UIC 指标对不同采样时间获得的评价指标均具有较好的一致性，计算结果不随着采样时间变化而变化，但GB/T 5599［12-13］中采用的立方频域算法则随着采样时间增大而减小，相同振动能量下该算法对于不同采样时间获得的评价指标是不一致的。

2.2 平稳性算法评价结果差异性机理分析

平稳性试验中，加速度信号由数据采集卡转换为数字信号后由计算机存储，而后通过傅里叶变换转换至频域，进行平稳性指标分析。由于测试获得的为有限离散点数据，进行离散傅里叶变换进行信号处理时，频率分辨率Δf可表示为

其中：Fs为采样频率；N为采样总点数；T为采样时间，N = T·Fs。

由式（4），离散傅里叶变换中，谱线将仅出现在频率分辨率Δf的整数倍上，即栅栏效应，未在Δf整数倍上的谱线则会按照能量不变的原则被分配到相近的Δf整数倍位置上，产生能量泄露［21］。图5 是栅栏效应和能量泄露对于周期信号的一个清晰示例，时域信号采样频率为100 Hz，当采样点数选取为700，采样时间长度是信号周期的整数倍，时频变换后，加速度幅值仅出现在1 Hz处。而当采样截止点不位于整数倍周期时，峰值频率发生偏移，且在相邻的频率处均有幅值，出现了能量泄露现象。此时，各个频率处的谱线幅值均方和仍为1，该现象可用式（5）所示的Parseval 定理证明，但其立方和将随着采样时间发生变化。轨道车辆车体的振动加速度是连续的随机信号，因此它的频谱应当是连续的，采样时间不可能同时为各连续频率的整数倍，因此总会存在栅栏效应和能量泄露。

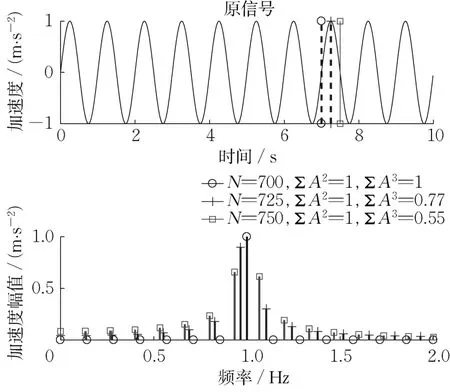
图5 时频变换的栅栏效应和能量泄露Fig. 5 Fence effect and energy leakage of time-frequency transformation

根据Parseval定理［7］，同一平稳随机信号的时域能量应当等于频域能量，即：

式中：x（n）为长度为N的离散时域序列；X（k）为x（n）的FFT（快速傅里叶变换）结果；A（k）为对应的幅值谱。

式（5）的左端项为序列的均方值E（x2（n）），对于一个平稳随机过程，E（x2（n））不随采样时间而变化，式（5）右端项为各谱线值的平方和，也是稳定的，如图5所示，这解释了无论采样时间长度如何变化，所有基于均方算法的指标都是稳定的，如ISO 2631-1和UIC 513 中规定的平稳性算法，因为计算得到的指标与车体振动的功率谱密度有严格的对应关系，而平稳随机信号的功率谱密度是不随采样时间长度而改变的，不受栅栏效应的影响。然而，如图5 所示，各采样时间长度得到谱线的立方和却是不稳定的，因为谱线立方和与信号的功率谱密度并未有对应关系，因此受到栅栏效应的影响，GB/T 5599中立方频域算法结果会随着采样时间的变化而变化。

3 基于统一频率分辨率的运行平稳性指标修正算法

立方频域算法不稳定的主要原因是平稳性指标与振动能量谱密度没有对应关系，即指标不满足能量一致性原则，导致指标受到栅栏效应的影响。而不同采样时间下的频率分辨率不同，导致栅栏效应和能量泄露现象对于信号中任意频率成分的影响强度均不同。虽然栅栏效应和能量泄露现象无法避免，但是仍可以选择固定的“栅栏”位置，使得对于任意采样时间的数据，其中相同频率成分受到栅栏效应影响强度相同。为使频率分辨率固定为Δf0，需要固定时域序列的总时间为

一旦参考时间长度T0确定，则频率分辨率即确定。对于采样时间大于参考时间长度的实测数据，可使用滑动平均的方式，将实测数据划分为多段进行运行平稳性指标计算后平均，且每段数据的长度Ti都应与参考时间长度T0相等。

实际测试中，往往会遇到的情况更多是采样时间不足，为不引入新的能量且不改变能量频域分布，使用末尾补零方法使时域序列达到参考时间长度T0。补零后的序列，在时域上总能量与原始序列相同，但时间长度被扩大为T0/T 倍，为保证其时域均方值不变，应当在补零之后再对其进行缩放，缩放因子为时，等效序列与原始序列拥有同样的均方值，定义新序列为x*（n），则有：

x（*n）的时域均方值为

因此，等效序列x*（n）在时域上的均方值与原序列x（n）相同，即补零后缩放不改变原序列的能量密度。此外，窗函数可以减少能量泄露［7］，以Hanning窗为例，使用仿真结果对比两种算法在不同采样长度处截取后的幅值谱平方和与立方和变化规律，如图6所示。

图6 不同采样时间的谱线幂方和Fig. 6 Power sum of spectrum of different sampling times

其中，使用Hanning 窗修正时有功率相等恢复系数1.633［7］，使用补0缩放算法时，统一修正至T0=100 s 的参考时间长度，当信号长度大于参考长度时，则使用滑动平均的方式分别计算各段的频谱幂方和并取平均值。

由图6a，直接截取、窗函数修正算法和补0缩放修正算法的谱线平方和∑（A2（k））都是一致的。由图7b，仅有补0缩放算法的谱线立方和∑（A3（k））具有一致性，窗函数修正算法和直接截取的计算结果呈现相同的单调递减结果。因此，针对栅栏效应和能量泄露现象导致的幅值谱立方和不稳定的现象，使用窗函数修正是无效的，而补0缩放算法修正是有效的。

将各实测数据的长度均调整至参考时间长度T0后，即可计算等效Sperling指标W*，该指标不随采样时间变化而变化，计算流程如图7所示。

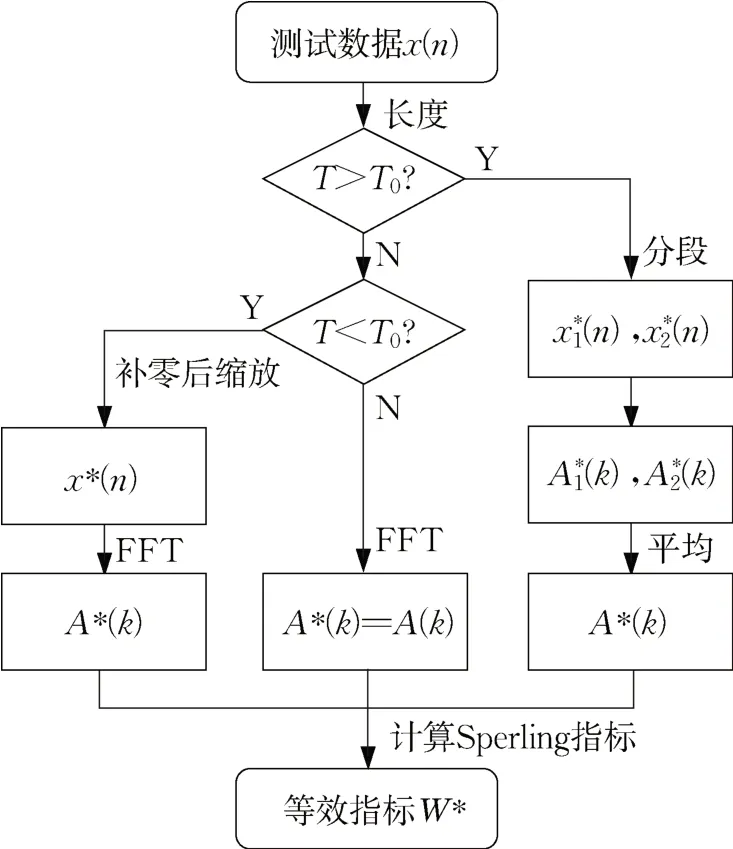
图7 等效Sperling指标W *计算流程图Fig.7 Flowchart of equivalent Sperling index W *

通过运行平稳性指标一致性修正算法，新旧版GB/T 5599被统一，且两标准中的指标可通过选择参考时间长度T0为5 s或18～20 s相互转换。修正算法还适用于非标准采样时间的平稳性评估，甚至是短于5 s的采样时间，以便反映非稳态冲击的影响。

4 平稳性指标一致性修正算法验证

为验证运行平稳性一致性算法的有效性，使用原算法与修正算法分别对仿真数据进行评估，运用修正算法时，参考时间长度T0取20 s，计算结果如图8 所示。由图可见，原立方频域算法的采样时间由2.5 s 增加至25 s 时，指标由2.62 下降至2.35，呈现出明显的单调递减趋势，而修正算法计算结果随采样时间变化基本保持一致，验证了该修正算法的有效性。

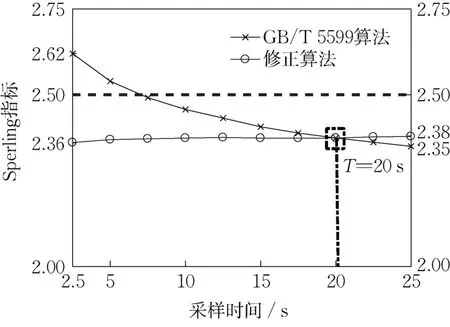
图8 不同采样时间的Sperling指标和修正指标Fig. 8 Sperling index and correction index of different sampling times

采样时间为5 s 与20 s 时，以及采样时间为5 s时基于能量一致等效修正算法下的频谱（T0=20 s），如图9 所示。由图可见，5 s 采样时间的幅值相比于20 s的幅值在各频率处更大。当采用修正算法计算5 s 采样时间的等效频谱后，使得谱线数量增加，频谱曲线与20 s采样时间的计算结果基本重合。采用该修正算法后，即使采样时间T 即频率分辨率Δf 改变时，立方和∑（A3（k））也仍然保持一致性。

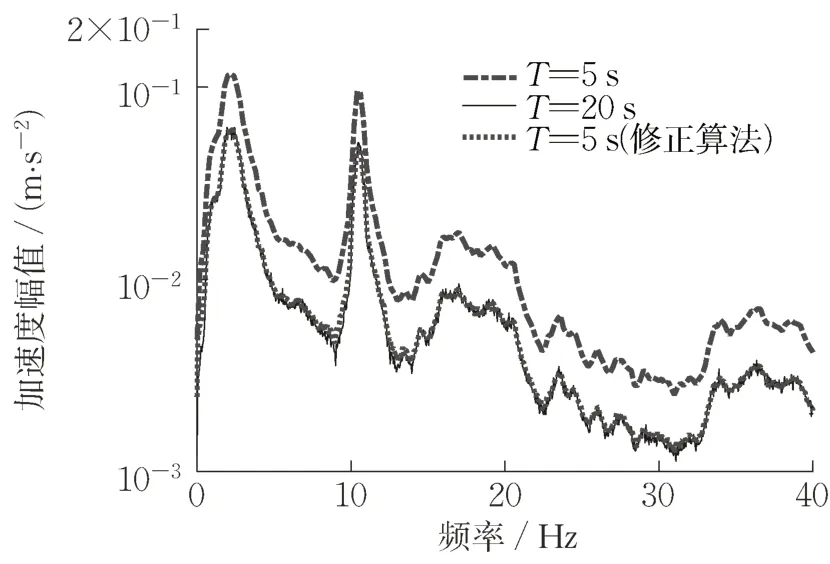
图9 不同采样时间下的频谱与等效修正算法频谱Fig. 9 Spectrum and correction spectrum of different sampling times

修正算法可将不同采样时间的运行平稳性指标全部修正至设定的参考时间长度下的指标，避免采样时间越长平稳性指标越低，采样时间越短平稳性指标越大这一不合理的现象，并以相同的限值进行评价。

5 结论

（1）ISO2631-1与UIC513标准的振动舒适性算法评价结果与采样时间无关，但基于频域立方算法的Sperling运行平稳性指标的GB/T 5599标准的计算结果，却随着采样时间的变化而变化，新版2019标准中规定将采样时间由18～20 s缩短到5 s，导致其平稳性指标结果较1985旧版标准的评价结果增大，常发生超出标准要求的情况；

（2）GB/T 5599标准中立方频域算法得到的平稳性指标评价结果关于采样时间的不一致性，是由于频谱幅值的立方和与平稳随机信号的能量密度没有保持一致，受到栅栏效应和能量泄露现象的影响，采样时间越长算得的指标越小。而基于均方算法的ISO2631-1与UIC513标准，根据Parseval定理，计算结果保持对采样时间的一致性；

（3）通过选取固定参考时间，提出基于统一频率分辨率的Sperling运行平稳性指标一致性修正算法，使得采样数据的频谱不随采样时间变化而变化，可消除立方算法的平稳性指标由于采样时间引起的差异；

（4）测试时可根据现场条件采样，然后分析时再选定参考时间长度，该方法同时可用于更短时的非稳态冲击影响。本文分析了GB/T 5599标准中采样时间长度不一致导致指标不一致的机理，为该标准的延续和改进提供了理论基础。

作者贡献声明：

张展飞，文献查阅，算法研究，软件操作，试验分析，数据采集，论文撰写与修改。

孙文静，基金资助，理论指导，验证分析，论文审阅与修改。

周劲松，理论指导，论文审阅与修改。

宫岛，试验指导。

王腾飞，试验分析，数据获取与处理。