高考中常见的含轻弹簧的题型剖析

陈维波

(山东省沂南第一中学)

弹簧作为物理学习中常见的研究对象,在高中阶段是一个非常重要的考查类型——轻弹簧模型.含有轻弹簧的题目在高考中时常出现,有必要对其进行总结分析,以提高学生的解题能力.

在高中阶段,很多研究内容都被“理想化”了,比如质点、轻杆、滑轮、理想气体等,轻弹簧也是一个理想化模型.它是一个不计自身重力、各处受力相等、弹力严格满足胡克定律、不受运动状态影响的理想化物理模型.

如图1所示,同一根轻弹簧处在四种不同情况下:甲图中轻弹簧左端固定;乙图中轻弹簧左右两端均自由;丙图中轻弹簧左端与一质量为m的物块连接且物块放在光滑水平面上;丁图中轻弹簧左端与一质量为m的物块连接且物块放在粗糙水平面上.除此之外,轻弹簧的自由端都受到一个水平恒力F的作用.根据轻弹簧的性质,我们知道四幅图中轻弹簧伸长量的关系为Δl甲＝Δl乙＝Δl丙＝Δl丁.

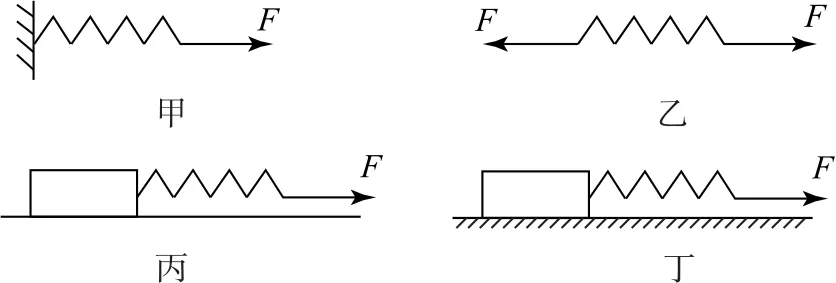
图1

以上简单回顾了轻弹簧的性质,接下来再看一下在高中物理学习过程中涉及轻弹簧的两种常见题型.

1 静力学问题常见题型

静力学问题是最基础、最简单也是最常见的题型,主要考查力的平衡问题,解题的关键是正确进行受力分析,确定轻弹簧对研究对象的弹力,然后利用平衡条件列方程求解.

图2

(1)轻弹簧的原长;

(2)金属环B与细杆间的动摩擦因数.

(1)如图3所示,对金属环A受力分析,由几何知识可得,解得.

设弹簧的压缩量为Δx,则有FT＝kΔx,解得.所以轻弹簧的原长为

(2)对金属环B受力分析如图3所示,因为其处于平衡状态,则由平衡条件,对沿右侧细杆方向可得

沿垂直细杆方向可得

【小结】在静力学问题中,弹簧的存在主要是提供弹力,解题的关键是正确判断弹力的方向,需具备的知识储备包括受力分析、力的合成与分解、胡克定律和几何知识.解题思路可归纳为:

第一步:确定研究对象,判断弹簧的状态,进而确定弹力的大小和方向.第二步:对研究对象进行受力分析,由于轻弹簧是理想模型,所以弹力的方向必然在弹簧所在的直线上.第三步:根据力的平衡条件列方程求解.

2 动力学问题常见题型

在动力学问题中涉及轻弹簧时,最常遇到的有三种情况:一是瞬时问题,即由于弹簧形变恢复需要时间,在轻弹簧受力发生变化内瞬间其形变未改变,可认为轻弹簧的弹力不变;二是在圆周运动中,弹簧不能视为轻绳,而是类似轻杆,但由于轻弹簧会被压缩,所以将其视为长度可变化的轻杆更合适;三是临界条件问题,轻弹簧不与研究对象连接时,临界条件就是轻弹簧恢复原长时对研究对象无弹力作用.

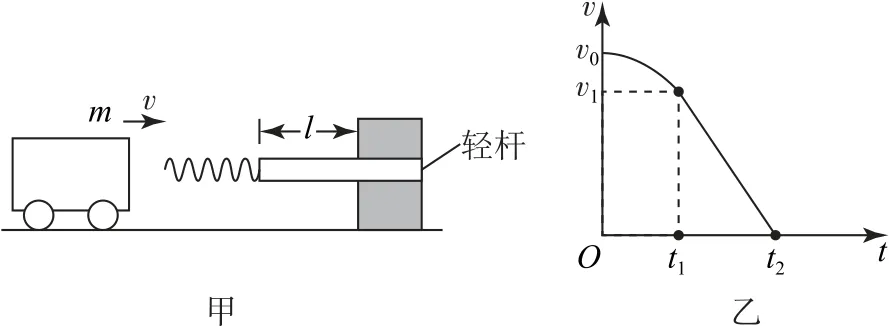
图4

A.小车在0～t1时间内的位移为

B.小车在时刻t1的速度为

C.轻杆在0～t2时间内由摩擦产生的热量为fl

D.在t1+t2时刻小车恰好与轻弹簧分离

想要轻杆向右移动,则需要弹簧的弹力达到轻杆与固定槽之间的摩擦力,则有f＝kx,在弹簧从初始状态到被压缩x长度后,到小车速度与轻杆速度相等,此时弹簧的压缩量达到最大值;随后轻杆、轻弹簧和小车组成的系统开始不断减速,直到静止;之后是小车在弹簧弹力作用下向左做加速运动.0～t1时间代表从弹簧刚开始被压缩到轻杆恰好开始运动的时间段,因此,该时间段内小车的位移即轻弹簧的压缩量,即,则可知选项A 错误.在0～t1时间内,轻弹簧弹力做功可以用平均力求解,由上面分析可知t1时刻弹簧弹力为f,对小车应用动能定理可得,解得,所以选项B错误.

轻杆在0～t2时间内相对固定槽的位移为l,故该过程中因为摩擦产生的热量为Q＝fl,所以选项C正确.

在0～t1时间内,小车做加速度增大的减速运动.在t1～t2时间内,小车、弹簧与轻杆一起做匀减速运动.最后小车被反弹做加速度减小的加速运动,此过程轻杆静止不动.结合平均速度分析可知小车从开始被反弹向左运动到与弹簧分离所用时间要大于t1,因此,在t1+t2时刻小车与弹簧还未分离,所以选项D错误.

【小结】在动力学问题中,分析弹簧与研究对象的关系及特殊时刻弹簧所处状态是关键.解题时,分析弹力和加速度的关系常用牛顿第二定律、胡克定律;分析速度、位移与加速度的关系常用运动学公式.其实,轻弹簧的加入,只是为动力学问题增加了一个力的变量,解题的整体思路并没有改变.

轻弹簧作为物理研究中的常见对象,以它为组成部分的题目并不限于以上类型,连接体问题、简谐运动问题、圆周运动问题、电磁感应问题等题目,也常有它的身影,我们不妨多总结归纳,必会对学习有所帮助.

(完)