揭秘晶体模型中的数学思维认知
史延宽
(山东省平度经济开发区高级中学)
高考试卷中涉及晶体结构与性质的命题,多以数学的思维方法进行推理解决.这类试题的一个共同点是将物质结构的特征通过“晶胞”的某种表征设计问题.因此,这类问题必须以“数学思维”为突破方法加以解决.
1 配位数的确定和密度的计算
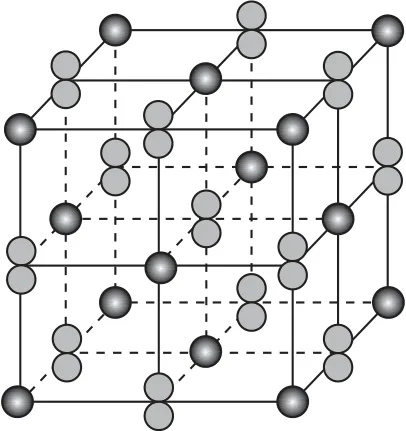
图1
(1)距离Fe2+最近的阴离子有________个.
(2)阿伏加德罗常数为NA.该晶体的密度为________g·cm-3.
分摊法:以1个顶角Fe2+为三维坐标原点(在晶胞中Fe2+占,即可以得到距离Fe2+最近的为,在3 个坐标轴上,为,故1 个Fe2+最近的阴离子有
(2)依据分摊法可知,晶胞中Fe2+个数为8×个数也是4.取1mol晶胞,则其密度为
【思维点拨】分摊法是从晶体中“提取”晶胞的一种手段,由微粒在几何形体的位置所决定,如正六棱柱中的顶角微粒在几何体中占.分摊法不仅仅适用于三维空间,也适用于二维平面,如钾的石墨嵌入化合物(图2-甲),利用分摊法将其分割为可以重复的规则平面几何形状(图2-乙),利用梯形或正六边形(2个梯形)可知其化学式是C12K.
2 微粒的确定和微粒间距离的计算
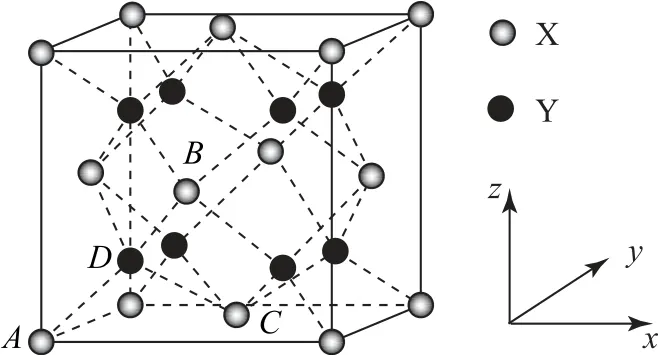
图3
(1)X 代表的离子是________.
(2)其中原子的坐标A为(0,0,0)、B为.则D的坐标为_________.
(3)若该立方晶胞参数为apm,正负离子的核间距最小为_________pm.
(2)据晶胞结构,可将晶胞分成8个相等的小正方体,其中包括ABCD,如图4所示,D在小立方体的体心,故坐标是
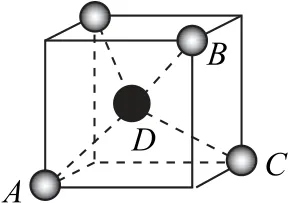
图4
【思维点拨】在利用距离公式法计算晶胞中两个微粒之间的距离时要注意:1)晶胞的几何体形状,若是平行六面体而不是正六面体,需要利用三角函数进行计算.2)要注意晶胞参数是否相同,不相同时,应将参数代入坐标进行计算.
3 平面投影的晶胞确定和参数计算
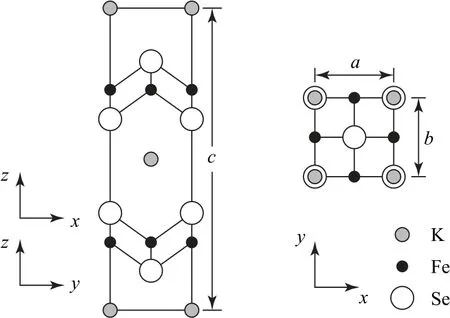
图5
(1)该超导材料的最简化学式为_________;
(2)Fe原子的配位数为________;
(3)该晶胞参数a=b=0.4nm、c=1.4nm.阿伏加德罗常数的值为NA,则该晶体的密度为________

图6
可知,该晶胞中K、Fe、Se的原子个数为2、4、4,其最简化学式为KFe2Se2.
(2)Fe原子的配位原子Se位于晶胞体内,故配位数是4.
(3)密度为
【思维点拨】对照还原法是将平面投影还原为晶胞结构的一种思维方法.利用同一微粒在不同平面的投影确定其在晶体中的位置(在图中标出位置即可,如图7-甲),不需要作出晶胞的图形(如图7-乙).
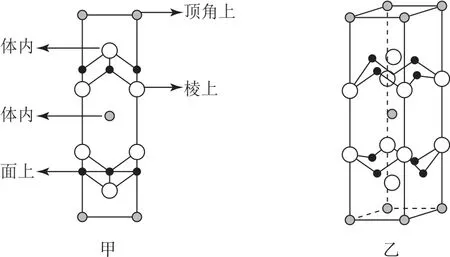
图7
通过以上典例不难发现,物质结构中的晶体结构是数学思维在化学中的应用,渗透了数形结合的基本思想,可以通过几何图形进行解读,也可以通过代数式进行诠释.具体方法有待于学生在做题过程中灵活把握,不拘一格.
(完)

