基于滚动优化的高载能工业园区优化调度策略

宋卓然，窦文雷，李剑峰，姜涛，芦思辰，季寒松

（1.国网辽宁省电力有限公司，辽宁 沈阳 110006；2.东北电力大学 电气工程学院，吉林 吉林 132012）

随着能源需求的不断增大，能源短缺问题和化石能源燃烧带来的环境污染问题日益严重[1-2]。为促进能源系统的低碳化转型，我国于2020年提出了“双碳”目标。在此背景下，可再生能源因其清洁性得到了大力发展。然而可再生能源出力的随机性和间歇性对配电系统运行的安全性和经济性带来了巨大挑战[3]。工业园区型微网因其能源消耗量大、供能区域集中和多能互补等特点成为了新能源发电消纳的主力军[4-5]。

分布式新能源接入工业园区后对工业园区自身的运行经济性也带来了新的挑战。目前针对单个工业园区运行经济性已有大量研究[6-19]。文献[6-10]通过考虑电池储能作用提高了工业园区的运行经济性。文献[11-12]中构建了工业园区内不同供能设备的需求响应模型，降低了工业园区的运行成本。文献[13-15]通过发掘园区需求响应能力提高了工业园区运行经济性。文献[16]提出了一种基于后悔度风险规避的随机生产任务和能量管理模型，降低了工业园区的运行成本。上述文献通过不同的优化调度策略提高了微网的运行经济性。然而，上述文献均对单一工业园区优化调度问题进行研究，忽略了配电系统和多个工业园区同时接入时对工业园区优化调度结果的影响，可能导致优化调度结果在多个工业园区同时接入配电系统的实际情况中无法应用。

针对含多微网配电系统的能量管理问题，文献[20]提出了一种含多工业园区的配电系统优化调度模型，降低了工业园区的用能成本。文献[21]提出一种基于双层规划的含多微网的配电系统优化调度模型，可以有效提高系统的运行稳定性和鲁棒性。文献[22-24]分别提出了不同的协同优化策略，通过协调各工业园区运行功率提高了各工业园区的运行经济性。文献[25]针对含多微网的配电系统提出一种新的交易策略，以提高系统整体的运行经济性。上述研究均是在单一时间尺度下对工业园区进行日前优化调度，通过一次求解下发调度周期内的所有控制指令，对可再生能源出力不确定性和负荷波动性的应对能力较差。

针对上述问题，本文提出了一种含多工业园区的配电系统能量管理策略。该策略同时考虑配电系统的经济性及其运行约束对工业园区优化调度结果的影响。其次，构建含多工业园区的配电系统两阶段优化调度模型，其中第一阶段为以系统总运行成本最小为目标函数的日前优化调度，求取工业园区设备的运行功率和配-微联络线功率；第二阶段为日内滚动优化调度，通过实时更新可再生能源出力和负荷预测值来降低预测误差，并基于最新数据对日前优化调度结果中配-微联络线功率进行追踪，以降低配-微联络线交互功率与日前计划值的偏差。最后，通过算例对所提模型和算法的有效性进行分析验证。

1 多工业园区配电系统协同优化调度框架

含多工业园区的配电系统框架如图1 所示。各个工业园区与配电系统通过不同节点相连，可以根据电价调节自身设备的运行状态，进而调整其与配电系统联络线上的交互功率，从而提高含多工业园区的配电系统总体运行经济性。

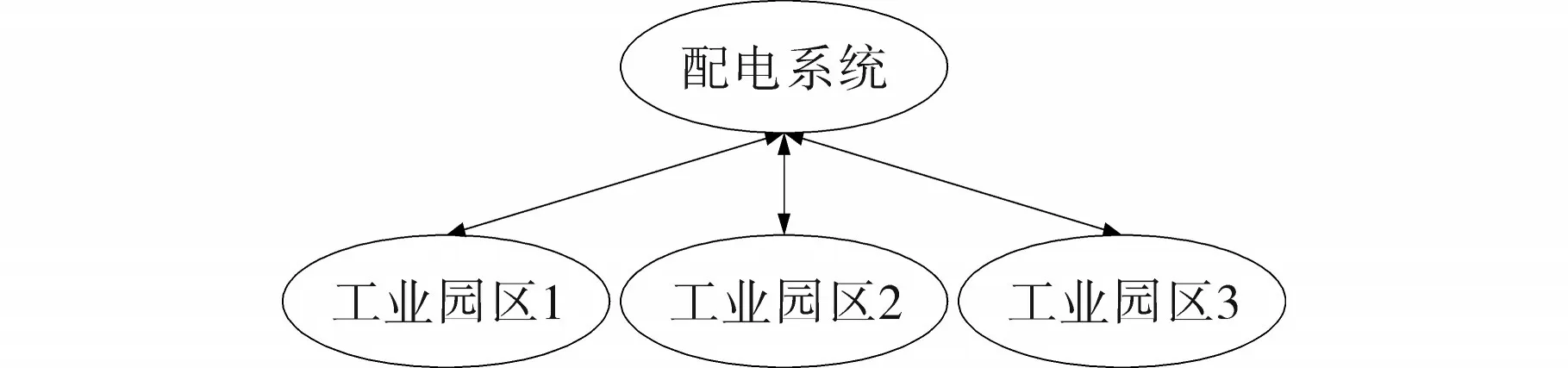
图1 含多工业园区的配电系统结构图Fig.1 Structure of distribution system with multiple industrial parks

工业园区内部供用能关系如图2 所示。其中，由空调系统和冰蓄冷系统对园区所需冷能进行供给；由微燃机和电锅炉对所需热能进行供给；由压缩空气系统对所需压缩空气能进行供给；由微燃机、光伏电源和配电系统对所需电能进行供给。此外，工业园区内部还包含电储能装置，利用该装置进行电能存储，以此改变不同时刻工业园区向配电系统的购电功率，进一步提升工业园区运行经济性。

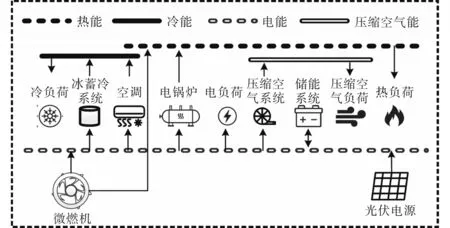
图2 工业园区供用能关系示意图Fig.2 Schematic diagram of energy supply and use relationship of industrial parks

2 多工业园区与配电系统日前协同优化调度模型

多工业园区与配电系统日前协同优化调度框架如图3所示。

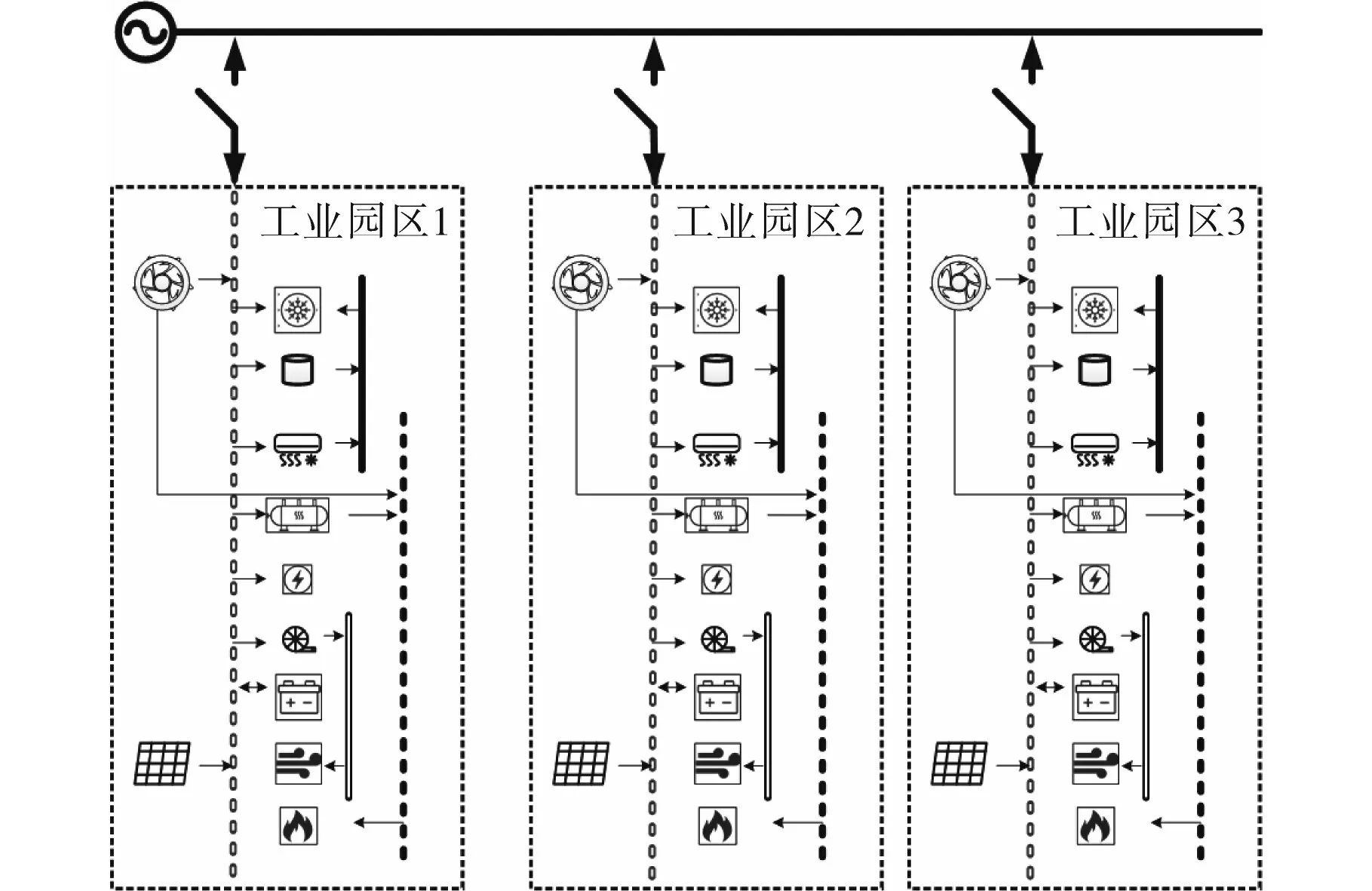
图3 含多工业园区的配电系统优化调度框架Fig.3 Optimization scheduling framework of distribution system with multiple industrial parks

各个工业园区根据电价对自身设备的运行状态进行调整，从而提高自身的运行经济性。同时，配电系统在满足潮流平衡等运行约束的情况下追求自身用能成本最小。因此，配电系统与各微网联络线功率会影响各工业园区与配电系统的优化调度结果。本节介绍通过协调联络线交互功率、配电系统和各工业园区内部设备的运行状态，提升含多工业园区配电系统运行经济性的含多工业园区的配电系统优化调度模型。

2.1 目标函数

目标函数为最小化含多工业园区的配电系统运行成本，如下式所示：

式中：Cobj为目标运行成本；下标“g”为第g台微燃机的相应变量；下标“t”为t时刻的相应变量；Ng为分布式微燃机的总台数；Nt为总时间；CDG，g，t，PDG，t分别为分布式微燃机的单位发电成本和发电功率；Ct，Pt分别为配电系统从上级电网的购电价格和购电功率；CM1，t，CM2，t，CM3，t分别为工业园区1、工业园区2 和工业园区3 从配电系统的购电价格；PM1，t，PM2，t，PM3，t分别为工业园区1、工业园区2 和工业园区3 从配电系统的购电功率；GasM1，t，GasM2，t，GasM3，t分别为工业园区1、工业园区2 和工业园区3 从配气系统的购气量；Cgas为工业园区从配气系统的购气价格。

目标运行成本包含配电系统从上级输电网的购电成本、配电系统分布式电源发电成本、各工业园区从配电系统的购电成本和各工业园区从配气系统的购气成本。

2.2 约束条件

2.2.1 配电系统约束条件

1）功率平衡约束。配电系统的潮流平衡约束受到各节点负荷、微燃机出力、配电系统从上级电网购电功率以及各微网负荷的影响，具体如下式所示：

式中：i，v1（j）分别为功率流向节点j的线路始端节点及所有始端节点合集；h，v2（j）分别为功率流出节点j的线路终端节点及所有终端节点合集；Pij，t，Qij，t分别为t时刻线路ij的有功、无功功率；PDG，j，t，QDG，j，t分别为t时刻与节点j所接的微燃机有功、无功出力；PD，j，t，QD，j，t分别为t时刻节点j除微网负荷外的其他负荷有功、无功出力；PM，j，t，QM，j，t分别为t时刻与节点j所接微网的有功、无功出力；lij，t为线路ij在t时刻电流的平方项；rij，xij分别为节点i与j之间的电阻以及电抗。

2）线路潮流约束的二阶锥形：

式中：Vi，t为t时刻节点i电压。

3）电压降方程：

4）节点电压上、下限约束：

式中：Vi,min，Vi,max分别为节点i电压幅值的最小、最大值。

5）线路传输容量约束：

式中：Pmaxij，Qmaxij分别为线路ij的最大有功、无功功率传输容量。

6）微燃机出力上、下限约束：

式中：PgDG,t，QgDG,t分别为微燃机g在时刻t的有功、无功出力；PgDG,min，PgDG,max分别为微燃机g有功出力的最小、最大值；QgDG,min，QgDG,max分别为微燃机g无功出力最小、最大值。

7）微燃机爬坡约束：

式中：Rup，Rdown分别为燃气轮机向上、向下爬坡速率。

2.2.2 工业园区约束条件

1）空调约束：

式中：Pminae，Pmaxae分别为空调运行功率的最小、最大值；Caet为空调的制冷功率；Paet为空调的运行功率；ηae为空调将电能转化为冷能的效率。

2）冰蓄冷系统约束。冰蓄冷系统中含有储冷罐、制冰机和融冰机，其约束包含储冷量等式约束、储冷量上下限约束、融冰功率上下限约束和制冰功率上下限约束，分别如下所示：

式中：Cact，Cact,min，Cact,max分别为t时刻储冷罐中的存储量、存储量最小值及存储量最大值；Pact，Pact,min，Pact,max分别为t时刻制冰机的运行功率及其运行功率的最小、最大值；Mact，Mact,min，Mact,max分别为t时刻融冰机运行功率及其运行功率的最小、最大值；ηp，ηM分别为制冰效率和融冰效率。

3）电锅炉约束：

式中：Hebt为电锅炉的制热功率；Pebt为电锅炉的运行功率；ηeb为电锅炉将电能转化为热能的效率。

4）微燃机约束：

式中：HMTt，PMTt分别为t时刻微燃机的热出力以及电出力；RMT为微燃机的热电比；ηMT为微燃机的运行效率；Hgas,t为微燃机用气量。

5）压缩空气系统约束：

式中：Gcast，Ecast，Pcast分别为储气罐储气量、时间Δt内的放气量及空气压缩机的运行功率；ηcas为压缩机制备压缩空气的效率；Gcas0为储气罐在初始时刻的储气量；Vcas为储气罐的体积；pcas,min，pcas,max分别为储气罐压强的最小、最大值；rvcast为0-1 变量，若压缩机运行则取1，否则取0；Pcasr为压缩机的额定功率。

6）光伏电源出力约束：

式中：PPVt为光伏电源出力；ηPV为光伏电源的光热转换效率；rPV为反射系数；Sri为太阳辐射强度；ΔSri为太阳辐射强度的预测误差。

7）蓄电池约束：

式中：SOCt为t时刻蓄电池荷电状态；SOCmin，SOCmax分别为蓄电池荷电状态的最小、最大值；SOC0，SOCend分别为蓄电池荷电状态的初始值与最终值；Pct为蓄电池充电功率；Pdt为蓄电池放电功率；，分别为蓄电池充电功率最小、最大值；，分别为蓄电池放电功率最小、最大值；Psoct为蓄电池运行功率。

8）能量平衡约束。能量平衡约束包含冷能、热能、压缩空气能和电能平衡方程，分别如下：

式中：Cloadt为工业园区冷负荷；ΔCloadt为工业园区冷负荷的预测误差；Hloadt为工业园区热负荷；ΔHloadt为工业园区热负荷的预测误差；Eloadt为工业园区压缩空气负荷；ΔEloadt为工业园区压缩空气负荷的预测误差；PM1t为工业微网1从配电系统购电功率；Ploadt为工业园区其他固定电负荷；ΔPloadt为工业园区其他固定电负荷的预测误差。

3 含多工业园区的配电系统日内滚动优化调度模型

传统的日前优化调度往往只进行一次求解就得出整个调度区间内的调度计划，对电价、负荷和新能源出力等不确定信息的预测误差和波动性的应对能力较差。因此，本文采用基于模型预测控制的滚动优化原理对含多工业园区的配电系统日内滚动优化调度模型进行求解，将调度区间分为多个预测区间和控制区间，在日内依次对每个预测区间进行求解，并只执行控制区间的调度计划，直至完成整个调度区间内的求解。通过日内优化调度可以有效降低不确定信息对优化调度结果的影响，提高配电系统对新能源发电的消纳。其中，日内滚动优化所采用的负荷、天气等不确定信息为基于最新时刻所预测的数值，与日前预测数据相比可降低预测值与实际值之间的误差，通过日内滚动优化实时更新工业园区的运行策略，从而实现校正作用。

不确定信息预测不准确性会使得配-微联络线功率产生波动，进而对配电系统功率分布产生影响，从而影响配电系统各节点电压和频率质量，为配电系统的运行安全性和可靠性带来挑战[26]。同时，当负荷发生突变时，可能会导致分布式电源爬坡速率达到上限，不利于配电系统的运行。为了消除联络线日内实际功率与日前计划值的偏差，将日前计划值作为跟踪项，以最小化预测域内联络线日内实际功率与日前计划值偏差量为目标函数构建含多工业园区的配电系统日内优化调度模型，目标函数如下式：

式中：Pobj为目标优化功率；PM1，PM2，PM3分别为日前调度计划中工业园区1、工业园区2 和工业园区3 在预测域内从配电系统的购电功率向量；PdayM1，PdayM2，PdayM3分别为日内调度计划中工业园区1、工业园区2 和工业园区3 在预测域内从配电系统的购电功率向量。

约束条件与式（2）～式（16）相同，不再赘述。

含多工业园区的配电系统日内滚动优化调度求解流程图如图4所示。

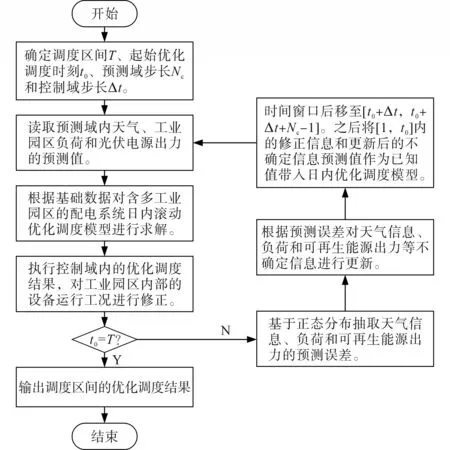
图4 含多工业园区的配电系统日内滚动优化求解流程图Fig.4 Flow chart for solving intra-day rolling optimal scheduling model of power distribution system with multiple industrial parks

含多工业园区的配电系统日内滚动优化调度具体流程如下：

1）确定调度区间T、起始优化调度时刻t0、预测域步长Nc和控制域步长Δt；

2）读取预测域内天气、工业园区负荷和光伏电源出力的预测值；

3）根据基础数据对含多工业园区的配电系统日内滚动优化调度模型进行求解；

4）执行控制域内的优化调度结果，对工业园区内部的设备运行工况进行修正；

5）判断t0是否等于T。若等于，则输出整个调度区间的优化调度结果；若不等于，转步骤6）；

6）基于正态分布抽取天气信息、负荷和可再生能源出力的预测误差；

7）根据预测误差对天气信息、负荷和可再生能源出力等不确定信息进行更新；

8）时间窗口后移至[t0+Δt，t0+Δt+Nc-1]。之后将[1，t0]内的修正信息和更新后的不确定信息预测值作为已知值代入日内优化调度模型，转步骤2）。

4 算例分析

4.1 基础数据

本文以IEEE-33节点配电系统与3个工业园区耦合的系统为例进行算例分析。工业园区1、工业园区2 和工业园区3 分别接入配电系统的6节点、18节点和26节点，拓扑结构如图5所示。

图5 IEEE-33节点配电系统与多工业园区耦合拓扑图Fig.5 Topology of IEEE-33 node power distribution system with multiple industrial parks

工业园区内部包含工业空调系统、冰蓄冷系统、电锅炉、微燃机、压缩空气系统、蓄电池及其他负荷（光伏电源等），设备具体参数见文献[5，16]。选取夏季某典型日进行优化调度，设置调度周期为24 h，日内滚动优化调度的滚动步长Δt为1 h。假设采取日前优化调度时天气和负荷的预测值与实际值之间存在期望为0、标准差为10%的随机误差，日内滚动优化时可将误差的标准差降低为3%。为分析考虑含多工业园区的配电系统需求响应特性前、后各工业园区的设备运行情况以及购电成本，设置以下场景：

场景1：不考虑多工业园区内部设备需求响应特性（内部设备采用固定工况运行，不对电价进行响应）。

场景2：考虑多工业园区内部设备需求响应特性。

为验证采用基于模型预测控制（model predictive control，MPC）的滚动优化原理进行求解时对抑制联络线功率波动性的有效性，设置场景2为以下2种场景：

场景3：考虑多工业园区内部设备需求响应特性，由于预测误差产生的联络线差额由外部电网进行补偿。

场景4：考虑多工业园区内部设备需求响应特性，由于预测误差产生的联络线差额由工业园区通过改变设备运行功率进行补偿。

4.2 日前优化调度结果分析

以下分析以工业园区1 为例，其余两个工业园区的设备运行情况与总购电功率结果分析与工业园区1类似，故不再赘述。

图6 为工业园区1 中供热设备的运行功率曲线图，包含微燃机与电锅炉。可以看出，在场景2下，在初期电价低谷时刻，由于采用微燃机进行发电和供热时价格较高，故微燃机一直处于运行功率下限，采用电锅炉和外部电网对工业园区内部的热能和电能进行供给；而在电价较高时刻，采用微燃机进行热能和电能的供给较为划算，在电价高峰时刻由于采用微燃机进行供热足够满足工业园区的热能需求，故电锅炉出力为0。通过上述策略可有效降低工业园区热能用能成本。

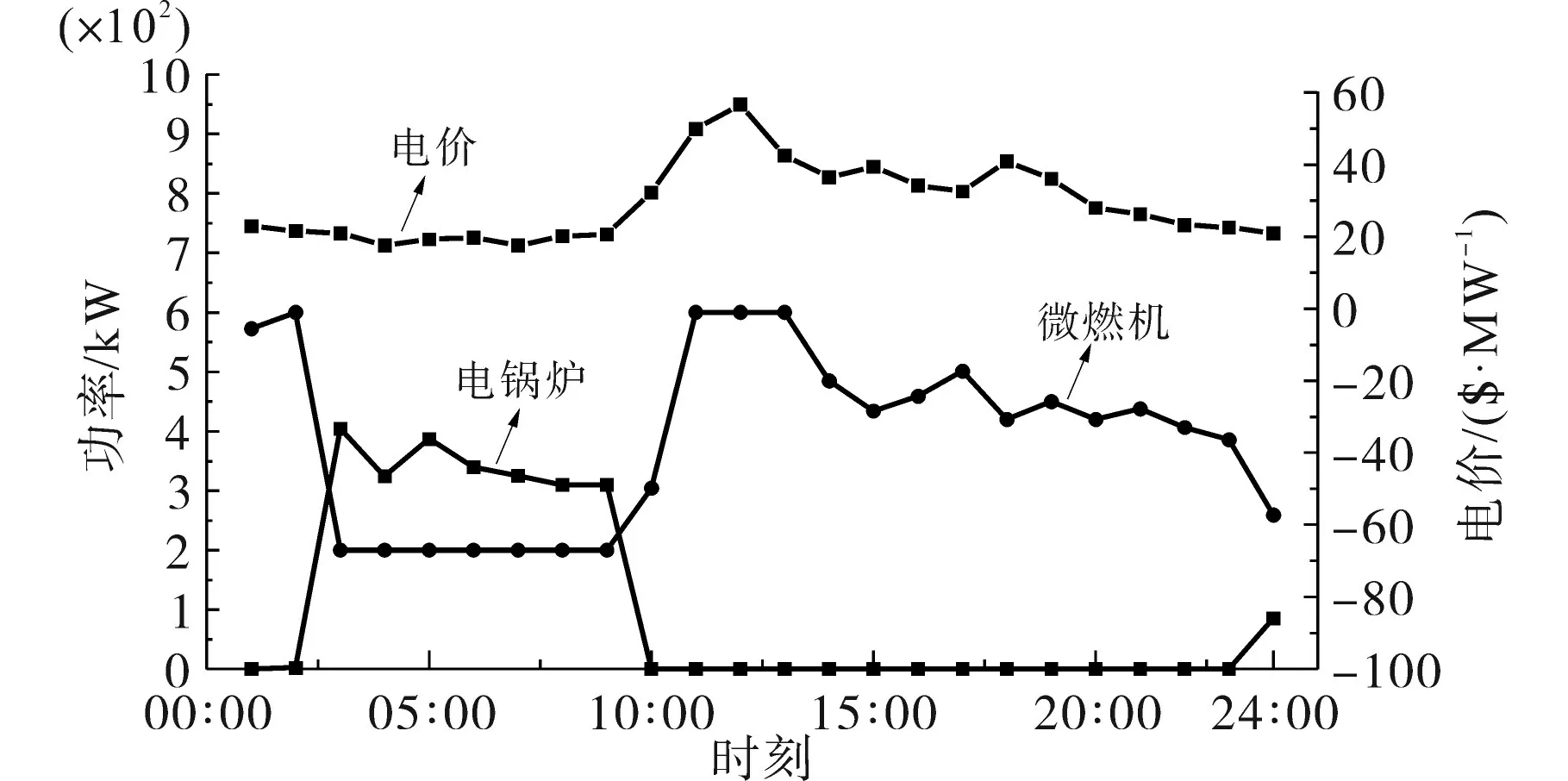
图6 供热系统运行功率Fig.6 Operating power of heating system

图7 为工业园区1 内部供冷系统的运行功率曲线。可以看出，在场景2下，电价低谷时刻主要使用空调进行制冷，同时，冰蓄冷系统处于制冰状态，将冷能进行存储；在电价峰时，即11：00—13：00 时间段，降低了空调系统的出力，通过冰蓄冷系统的融冰过程将存储的冷能释放出来以供给工业园区的冷能需求，有效地降低了工业园区供冷系统的运行成本。

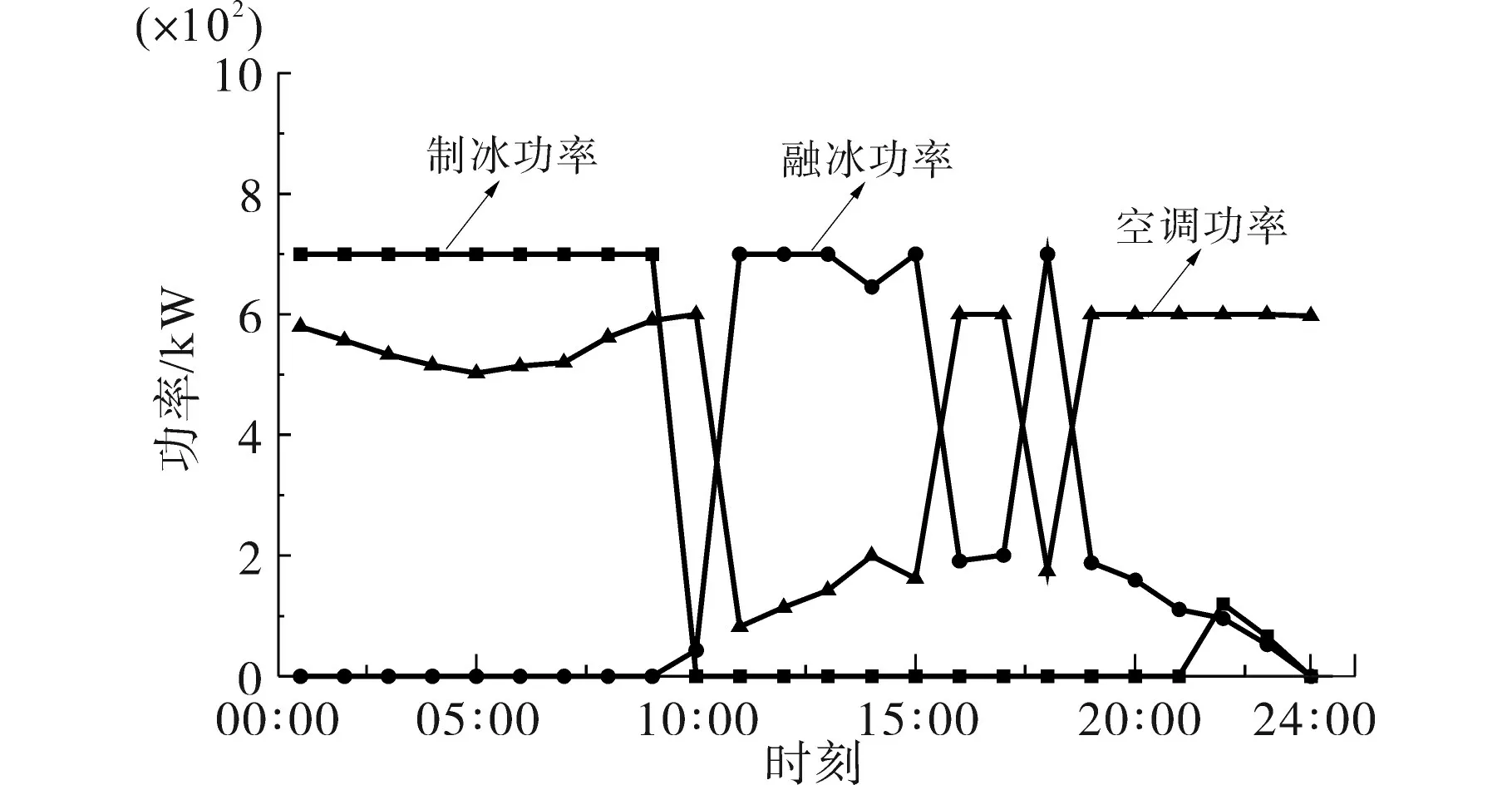
图7 供冷系统运行功率Fig.7 Operating power of cooling system

图8 为工业园区1 内部蓄电池的充放电功率曲线图。可以看出，在电价较低的00：00—09：00时间段，蓄电池由于自身容量的限制并未一直处于充电状态，而是选择在电价最低的04：00—05：00 及07：00 时间段进行充电。在电价高峰时刻，即11：00—13：00，15：00 及18：00—19：00 时间段将存储的电能释放出来供给自身使用，以降低电价高峰时刻自身的购电功率。通过蓄电池充放电过程对工业园区不同时刻购电功率进行调整，有效地降低了工业园区的购电成本。

图8 蓄电池运行功率Fig.8 Operating power of battery

图9 为工业园区1 在调度区间内从配电系统的购电功率曲线图。由图9 可以看出，相较于场景1，场景2 下的工业园区在电价高峰时刻，即11：00—12：00，15：00 及18：00 时间段的购电功率均出现了明显的降低，将部分耗能过程转移到了电价低谷时刻。通过本文所提策略，工业园区1在24 h内的购电成本相较于场景1降低了35.7%。

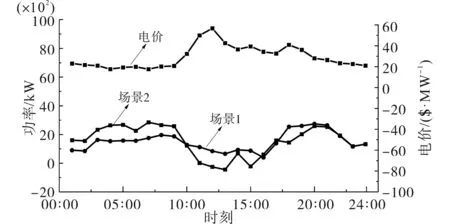
图9 工业园区1从配电系统购电功率Fig.9 Purchases power from the distribution system by industrial park 1

为更加直观地对场景1 和场景2 下各工业园区的购电成本进行分析，表1给出了场景1和场景2 下各工业园区的购电成本。可以看出，相较于场景1，场景2下工业园区1、工业园区2和工业园区3从配电系统的购电成本分别降低了299.2＄，322.3＄和231.2＄。

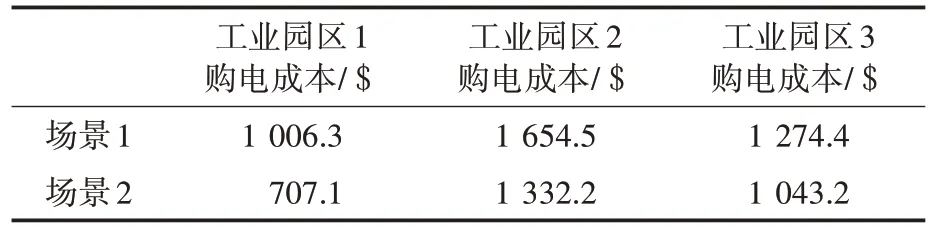
表1 场景1和场景2下各工业园区运行成本Tab.1 Costs of each industrial park under scenario 1 and scenario 2

4.3 日内滚动优化调度结果分析

分析日内滚动优化时场景3 和场景4 下工业园区与配电系统联络线功率与日前优化配-微联络线的功率偏差，图10 为场景3、场景4 下日内滚动优化工业园区1配-微联络线的功率曲线图，其余两个工业园区联络线结果与其类似，故不再赘述。由图10 可以看出，相较于场景3，在场景4下，日内滚动优化各个时刻配-微联络线交互功率与日前优化配-微联络线功率的偏差值明显降低。对于00：00—07：00 和18：00—24：00 时间段，由于此时仅存在各个工业园区自身冷、热、电负荷的预测偏差，而不存在光伏电源出力的偏差，故场景4 较于场景3，配-微联络线功率与日前计划下的配-微联络线功率偏差值减小得不明显。在08：00—18：00时间段，同时存在上述两种预测偏差，故场景4 相较于场景3，配-微联络线的功率偏差值降低较为明显。通过上述策略，可有效降低实际运行情况下各工业园区从配电系统的购电功率与日前计划值的偏差，有效抑制了由于预测误差导致的配-微联络线功率波动。

图10 日内滚动优化时工业园区1从配电系统购电功率Fig.10 Purchases power from the distribution system by industrial park 1 under intra-day rolling optimization

图11为场景3与场景4下各发电机的出力曲线图。由图11 可以看出，在场景3 下，由于需要配电系统改变分布式电源出力对预测误差导致的功率波动进行补偿，各分布式电源的出力波动较大，在09：00—11：00 时间段，由于预测误差导致的功率波动较大，分布式电源出力出现了明显波动，其功率变化已经达到了爬坡速率的限值，剩余功率波动需要通过调整从上级输电网的购电量来满足功率平衡，不利于配电系统运行的经济性和可靠性。而在场景4下则通过工业园区对功率波动进行补偿，配电系统内分布式电源出力变化较为平缓，且拥有一定裕度，更加有利于配电系统运行的安全性和可靠性。

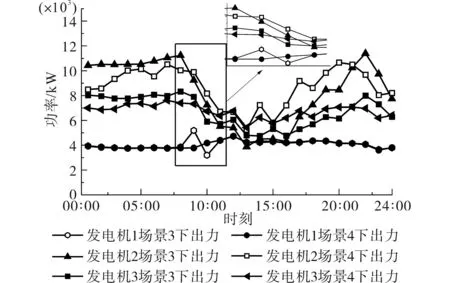
图11 分布式电源出力Fig.11 Power of distributed generation

图12为各配-微耦合节点在调度区间24 h内的电压水平。由图12 可以看出，在场景3 下，由于联络线功率波动由配电系统进行补偿，当预测信息波动较大时会对配电系统的潮流平衡产生影响，从而影响配-微耦合节点的电压水平，在09：00—11：00 时间段，配-微耦合节点电压出现了明显波动，不利于工业园区内部设备的正常运行。而场景4 下各配-微耦合节点电价基本处于无波动状态。由上述分析可知，在场景4下，通过工业园区改变设备运行状态对预测误差造成的联络线功率波动进行补偿时更加有利于配-微耦合节点的电压质量，能够更好地保证工业园区内部设备的正常运转。

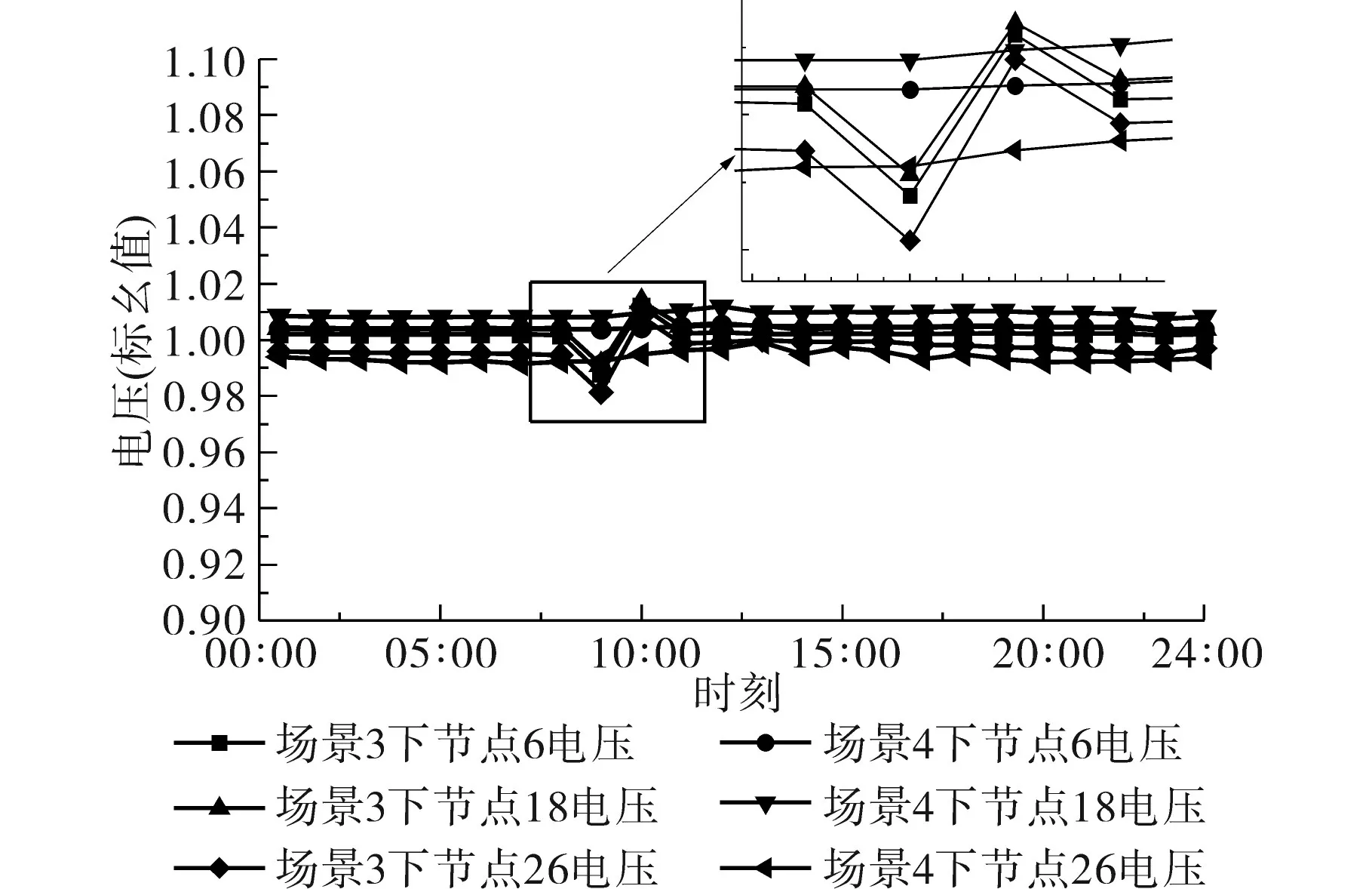
图12 配网与工业园区耦合节点电压Fig.12 Voltage of coupling nodes of distribution system and industrial park

表2 为场景3 与场景4 下各工业园区的购电成本。由于工业园区的购电成本主要取决于其向配电系统的购电功率，场景4 下工业园区通过改变自身设备运行功率对联络线功率波动进行补偿，联络线功率与日前优化调度中联络线功率相近，故各工业园区购电成本与日前优化调度相近。而场景3下则通过外电网对联络线功率波动进行补偿，工业园区仍以自身运行经济性最优为目标，故成本进一步降低。由此可以看出，当工业园区通过改变自身运行功率对联络线功率波动进行补偿时会牺牲一定经济性。为增强工业园区参与联络线功率波动补偿的积极性，可采用合理的奖励、惩罚机制[27-29]。且通过对图12 分析可知，在场景4 下配-微耦合节点的电压质量更好，更加有利于工业园区设备的运行，也可在一定程度上增加工业园区参与联络线功率波动补偿操作的积极性。

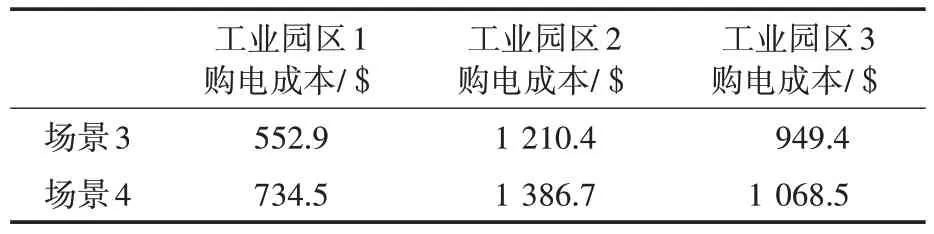
表2 场景3和场景4下各工业园区运行成本Tab.2 Costs of each industrial park under scenario 3 and scenario 4

5 结论

分布式新能源出力不确定性为配电系统运行安全性和经济性带来了挑战，基于工业园区可有效整合各类分布式新能源这一特点，本文提出了一种含多工业园区的配电系统多时间尺度优化调度策略；构建了以运行经济性最优为目标的含多工业园区的配电系统日前优化调度模型和以联络线功率偏差最小为目标的含多工业园区的配电系统日内滚动优化调度模型。

由算例分析可知，本文所提的含多工业园区的配电系统多时间尺度优化调度策略，可以有效降低各个工业园区的购电成本，其中工业园区1、工业园区2 和工业园区3 分别降低了35.7%，19.5%和18.2%。通过含多工业园区的配电系统日内滚动优化调度策略，有效地抑制了由于日前预测误差而导致的实际运行情况下配-微联络线交互功率的波动，保证了配电系统各节点的电压质量和运行安全性。