基于SAC和TD3的含电动汽车虚拟电厂调度策略

陶力，杨夏喜，顾金辉，魏兵兵，张琳，王嘉宁

（1.华北电力大学 经济与管理学院，北京 102206；2.南瑞集团有限公司（国网电力科学研究院有限公司），江苏 南京 210003；3.苏州市产品质量监督检验院，江苏 苏州 215104；4.华北电力大学 电气与电子工程学院，北京 102206；5.北京科东电力控制系统有限责任公司，北京 100194）

由于电动汽车（electric vehicle，EV）具有低能耗、低排放的优势，预计其接入电网的比例持续增加。电动汽车能够借助充电桩实现与电网之间的互动（vehicle to grid，V2G），在减少用户成本的同时，起到辅助电网安全稳定运行的作用[1]，是一种非常有潜力的分布式电源（distributed energy resource，DER）。然而，由于EV 接入电网的时空不确定性，其入网充电时间与充电电量均具有较高的随机性，这也给电网优化控制带来了极大的挑战。

针对EV 充电的优化问题，文献[2]对用户取车时的目标电池荷电状态（state of charge，SOC）做出约束，提出采用双延迟深度确定性策略梯度（twin delay deep deterministic policy gradient，TD3）算法连续控制充电桩的充电功率，但是没有考虑到充电管理系统能够提高实际充电时的效率；文献[3]采用深度Q 网络算法控制EV 的充电行为，能够降低充电费用及平抑网络功率波动，但是这种算法只能用于充电功率的分档调节；文献[4]将电动汽车充、放电调度问题建模为带约束的马尔可夫决策过程，然后采用提高强化学习安全性的约束型策略优化（constrained policy optimization，CPO）算法求解；文献[5]将电动汽车实时电压控制问题转化为EV 无功控制和V2G 两种模式的马尔可夫博弈，并采用深度确定性策略梯度（deep deterministic policy gradient，DDPG）算法求解，效果较好。上述基于深度强化学习（deep reinforcement learning，DRL）的方法利于EV充电站内部优化，但无法通过与传统运筹学模型相结合来与外部资源联合优化。

与此同时，随着分布式能源、储能、通信、并行计算等技术的发展，含电动汽车的虚拟电厂（VPP）可以将分布式可再生能源发电、储能装置、电动汽车等资源聚合成一个整体，作为一个特殊的电厂参与电力市场竞争[6-8]。文献[9]提出风电商和EV 聚合商通过合作博弈组成VPP 参与电力市场投标竞争，并采用Shapley 值法进行收益分配。文献[10]提出以VPP 为售电商的EV 主从博弈模型，能够优化自身售电策略，并引导EV 有序充电。然而此类电力市场模型往往呈现非凸、非线性、维度高的特点，采用传统运筹学方法求解时难度较大。系统中可再生能源的间歇性以及电动汽车负荷需求的不确定性造成了供需双方的随机波动，传统的调度方法难以准确地适应实际环境的动态变化，也难以对智能体控制的EV充电站优化调度。

随着人工智能技术的发展，DRL 方法在电力系统中也越来越受到重视[11-13]，其可以模拟不完全信息的交易或博弈，能从高维、连续的状态空间中提取高阶数据特征，对含不确定性的可再生能源出力、电动汽车有序充电、电力市场交易等模型有较强的表达及特征挖掘能力。文献[14]采用DDPG 算法，以解决VPP 经济调度问题的最优解，但没有考虑电动汽车充电，也没有考虑VPP在日前市场的交易。文献[15]采用基于优先经验回放的深度确定性策略梯度（deep deterministic policy gradient with prioritized experience replay，DDPG-PER）算法作为电力市场竞价策略，当出清模型非凸时，获得的收益超过数学规划方法。此外，无模型的深度强化学习算法也已被应用于求解Nash 博弈[16-17]、Stackelberg 博弈[18-19]、平均场博弈（mean field games，MFG）[20]等多种博弈论模型。

从现有文献来看，传统博弈论方法一般局限于求解完全信息静态博弈问题。传统的强化学习（reinforcement learning，RL）算法虽然可以动态模拟不完全信息的重复博弈，但应用范围局限于低维的离散状态/动作空间，且收敛结果不稳定。本文针对含EV 充电站、分布式机组、储能、可再生能源等灵活性资源的VPP，提出基于深度强化学习的VPP 与EV 主从博弈模型，其中VPP 采用柔性行动器-评判器（soft actor-critic，SAC）算法，EV 聚合商采用TD3 算法。VPP 整合配电网内分布式能源并制定合理的售电策略来引导EV 的有序入网，以实现多种新能源间的协调互补与整体优化。本文的主要贡献如下：

1）对于智能体优化控制的VPP 与EV 充电站构成的主从博弈模型，提出交替训练行动器-评判器算法网络参数的求解流程与方法。

2）算例从博弈论中策略类型的角度，研究了混合策略与纯策略在模型中的不同效果，并给出了初步的解释。

3）算例对比了博弈与不博弈下模型的结果，表明主从博弈模型能降低EV 用电成本，提高社会福利。

1 电力市场交易流程及VPP结构

VPP服务器利用通信技术将可控分布式发电机组、风电、光伏、储能及电动汽车充电站等资源聚合，形成整体参与电网市场交易及电网运行。VPP 容量较小，可作为价格接受者参与日前电力市场（day-ahead market，DAM）和实时平衡市场（real-time balancing market，RBM）的电力交易[21]。

1.1 含VPP电力市场交易流程

电价机制采用市场清算电价（pay-as-bid，PAB），其规则[22]如下：在第n天的能量市场交易结束之前，VPP 以系统运营商（independent system operator，ISO）的出清结果为日前电力市场价格曲线，根据对电动汽车负荷量、可再生能源发电量的预测，通过与EV 主从博弈产生的均衡解，形成VPP 日前优化与实时调度的控制策略。并依据训练好的深度强化学习模型，向ISO 独立申报第n+1 天24 个交易时段的电量交易信息。在随后的实时平衡市场中，VPP 根据EV 以及新能源机组的实时功率波动，调整内部储能与可控分布式机组（distributed generator，DG）的出力、EV充电电价以降低功率偏差，对于无法平衡的功率偏差则在实时平衡市场中以惩罚电价进行交易。

VPP 在日前电力市场中的购电策略可以表示为PD={P1D,P2D,…,PTD}，其购电成本CBt为

式中：PDt，PRt为VPP 在日前电力市场和实时平衡市场中的购电/售电量；PDmin，PDmax为购售电量上、下限，与联络线功率约束有关；λDt为日前电力市场的出清价格，由ISO 在日前根据出清结果确定；为实时平衡市场中的惩罚性购售电价[10]。

1.2 VPP结构及数学模型

VPP 作为一个整体对外参与电力市场，对内实现各DER、储能、EV 充电站的协调运行控制，可以提高在电力市场中的竞争力[23]。

1.2.1 EV充电站

本文考虑一个包含K个充电桩、完全由智能体控制的EV 充电站，其中第i台EV 充、放电的数学模型如下所示：

式中：PEVi,t为t时刻充、放电功率，PEVi,t≥0代表EV 充电量，PEVi,t＜0 代表放电量；ta,i，tl,i分别为EV 的到达、离开时刻；ei,t，ei,t,min分别为第i台EV在时刻t的SOC 和满足用户要求的最低SOC；emax，emin分别为EV 电池容量限制的最大SOC 和最小SOC；en为电动汽车出发时期望的最小SOC；ηche，ηdise分别为EV电池的充、放电效率；Qe为电池总容量；Δt为时间间隔；，分别为充、放电功率Pchi,t和Pdisi,t的最大值。

充电站中不同EV 在每个时段内的充、放电功率由同一个充电站智能体控制。充电站智能体依次观察每台EV 当前的状态，并确定下个时刻EV 的动作。第i台EV 的状态包括当前时间、充电站内充电桩使用率、VPP 制定的EV 充电价格、第i台EV 的SOC、第i台EV 预计剩余的取车时间，即

其动作为每台EV在t时刻充、放电量，即

1.2.2 分布式机组发电

可控分布式机组一般为用户侧的小型燃气机组或柴油机组，运行成本CDGi,t主要考虑发电成本CDG1i,t、启停成本CDG2i,t，其运行特性与约束条件为

式中：PDGi,t为第i台分布式机组在t时刻的输出功率为机组的启停状态，1表示运行，0表示停运；aDGi，bDGi，cDGi分别为第i台分布式机组的耗量参数；coni，coffi分别为第i台常规机组的启动和停机成本；，分别为DG 输出功率上、下限；ΔPDGi,t为功率变化量；，分别为分布式机组爬坡速率上、下限。

式（9）为分布式机组成本耗量函数，式（10）为输出功率约束，式（12）约束分布式机组功率调整的爬坡速率。

1.2.3 储能

本文储能单元的运行特性与约束条件为

式中：PESi,t为储能充放电量，PESi,t≥0 代表充电量，PESi,t＜0 代表放电量；fESi,t为t时刻在储能单元中存储的能量分别为储能单元的最小、最大容量分别为一天开始与结束时刻储能单元的能量；ηchb，ηdisb为储能单元的充、放电效率。

1.2.4 可再生能源发电

风电聚合商在日前给出预测的24 h 风电出力。风力预测相对误差通常大于负荷预测的相对误差，且该误差的标准差随着预测水平的增大而增大。本文保守估计其误差服从均值为0、标准差为δ的正态分布[24]。其出力可表示为

式中：Pwr,i,t为风电在t时刻的功率实际值；Pwf,i,t为风电在t时刻的功率预测值；Δpw,i,t为风电功率预测误差；δw,i,t为风电在t时刻的风电出力预测误差标准差；Qw,i为风电装机容量。

风电设备的建造成本为一次性投入，本文将其忽略。

2 VPP与EV主从博弈模型

在Stackelberg主从博弈[25]中，假定博弈中的所有参与方都为理性人，以使己方利益最大化为目标。领导者先提出一个策略，然后跟随者根据领导者采取的策略，调整策略使自己的效用最大化。

在本文中，假定VPP 为博弈主体，EV 为博弈从体，根据DRL 算法，得出每个博弈主体的最佳策略。各主体与环境相互作用，以优化其长期奖励为目标进行策略的学习。VPP 的控制变量为{λEVt，PESi,t，PDt，PDGi,t，∀i，∀t}，其目标函数和约束条件如下：

式中：CEVt为整个充电站的用电成本，即VPP 从EV 获得的收入；λEVt为VPP 制定的t时刻EV 的充、放电价格，满足对应时刻的价格上、下限约束；LVPPt为VPP各约束的惩罚项。

训练时，为处理模型中的等式约束，本文引入LVPPt作为VPP各约束的惩罚项，其表达式为

式中：αEV，αES为惩罚项的系数，取值为足够大的正数，以激励智能体满足模型约束。

训练中，为引导智能体满足每辆EV 的SOC不等式约束，引入LEVt作为惩罚项，其计算公式为

式中：β为惩罚项的系数。

本文中，VPP 的状态为时间、微型汽轮机发电量、电动汽车充电站充电桩使用率、储能SOC、DAM 电价、电动汽车充电站的电价累计值、风电功率预测值，即

VPP 的动作为微型汽轮机发电变化量、电动汽车充电站充电价格、储能动作、日前售电量，即

3 基于深度强化学习的模型求解

强化学习基本框架如图1所示。

图1 强化学习基本框架Fig.1 Basic framework for reinforcement learning

3.1 行动器-评判器算法框架

行动器-评判器（actor-critic，AC）框架是强化学习连续动作领域的一类重要算法，包含了DDPG 算法[26]、TD3 算法[27]、SAC 算法[28]等多种无模型（model-free）的、离轨策略（off-policy）的算法。其中，DDPG与TD3为确定性策略，SAC为随机性策略。

3.1.1 优化目标

强化学习算法的训练目标为通过与环境互动，寻找最优策略π*，使得智能体在有限马尔科夫决策过程（Markov decision process，MDP）[29]中，累积回报的期望最大，即

式中：τ为策略π在环境中形成的状态-动作轨迹，即τ=(s0,a0,s1,a1,…)；R(τ)为智能体在每幕的总回报；rt为时刻t的回报。

策略则由参数为θ的神经网络表示，本文将确定性策略记为μθ(s)，即a=μθ(s)；将随机性策略记为πθ(·|s)，即a～πθ(·|s)。

为提高算法的探索能力，防止过快收敛，SAC算法采用了熵正则化，其目标函数为

式中：α为温度系数，即熵项的权重；H为在策略π、状态st下采取动作的熵项。

其贝尔曼方程（Bellman equation）为

式中：Vπ(s)为状态值函数；γ为奖励折扣因子，表示一个状态的价值由该状态的奖励以及后续状态价值按一定的衰减比例求和组成。

在强化学习中，为得到最优策略π*，核心思想是用价值函数来对最优策略进行结构化搜索，通过迭代策略评估来寻找满足贝尔曼方程的最优价值函数（optimal value function）V*和Q*。

3.1.2 动作的选择

智能体的动作由当前Actor 网络的输出决定。对于确定性策略算法，为增加对环境的探索能力，对输出动作加噪处理，即

式中：clip()为将动作限制在[aL,aH]范围内。

对于随机性策略算法，智能体的动作由网络输出参数确定的分布决定，即

3.1.3 网络的更新

AC框架的网络由策略网络（actor）、价值网络（critic）、目标策略网络、目标价值网络组成，其参数分别用θ，ϕ，θtarg和ϕtarg表示。策略网络采用策略梯度方法，进行梯度上升更新，用于建立由状态st到动作at的映射，对于DDPG 和TD3，假如从缓冲记忆库D中抽取一批数据B=[(s,a,r,s′,δ)]，其网络参数更新梯度为

对于SAC，其网络参数更新梯度为

其中，为了使得式（38）可微，͂(s)为通过重参数化技巧（reparameterization trick）得到的动作，本文采用挤压高斯策略（squashed Gaussian policy）获得，即

式中：⊙为向量间对应元素相乘。

价值网络相当于传统强化学习算法中的状态值函数，即从初始状态出发得到的期望累积回报，采用梯度下降方法更新，目的是对策略网络建立的映射作出评价，即进行Q值估计。对于DDPG，其网络参数更新梯度为

其中

式中：y(r,s′,d)为目标。

对于TD3 和SAC，为避免出现DDPG 中常见的价值高估问题，采用两个结构相同的价值网络估算Q值，并取最小值，其网络参数更新梯度为

对于TD3，有：

对于SAC，进一步采用了熵正则化技巧：

目标策略网络、目标价值网络的参数分别从策略网络、价值网络软更新，即

式中：τ为更新参数，本文取0.005。

3.2 含EV的VPP调度的深度强化学习算法流程

本文建立的模型中，EV 充电站采用TD3 算法训练智能体，而VPP 采用SAC 算法训练智能体。这两个智能体之间存在主从博弈关系。

本文采用交替训练的方法来模拟VPP 与EV充电站多阶段博弈过程。为提高训练稳定性，VPP向EV售电价格采用软更新方法，计算公式为

式中：ξ为更新系数，本文取0.01。

在完成上述计算后，VPP 在整个训练过程中，智能体可以记录训练过程中的日前电力市场购售电量的滑动平均值PˉDt作为在日前向ISO 申报的实际购售电量。

4 算例分析

在一个包含可再生能源、储能、分布式发电、电动汽车等资源的VPP 中验证本文采用的强化学习方法。风电、电价曲线均取自北欧电力市场瑞典中南部地区2020 年6 月7 日的数据[30]，并按汇率进行调整。

可再生能源平均出力及DAM 电价曲线如图2所示。

图2 可再生能源平均出力及DAM电价曲线Fig.2 Renewable energy average output and DAM tariff curve

电动汽车充电负荷曲线来自文献[31]。电动汽车数量曲线如图3所示。

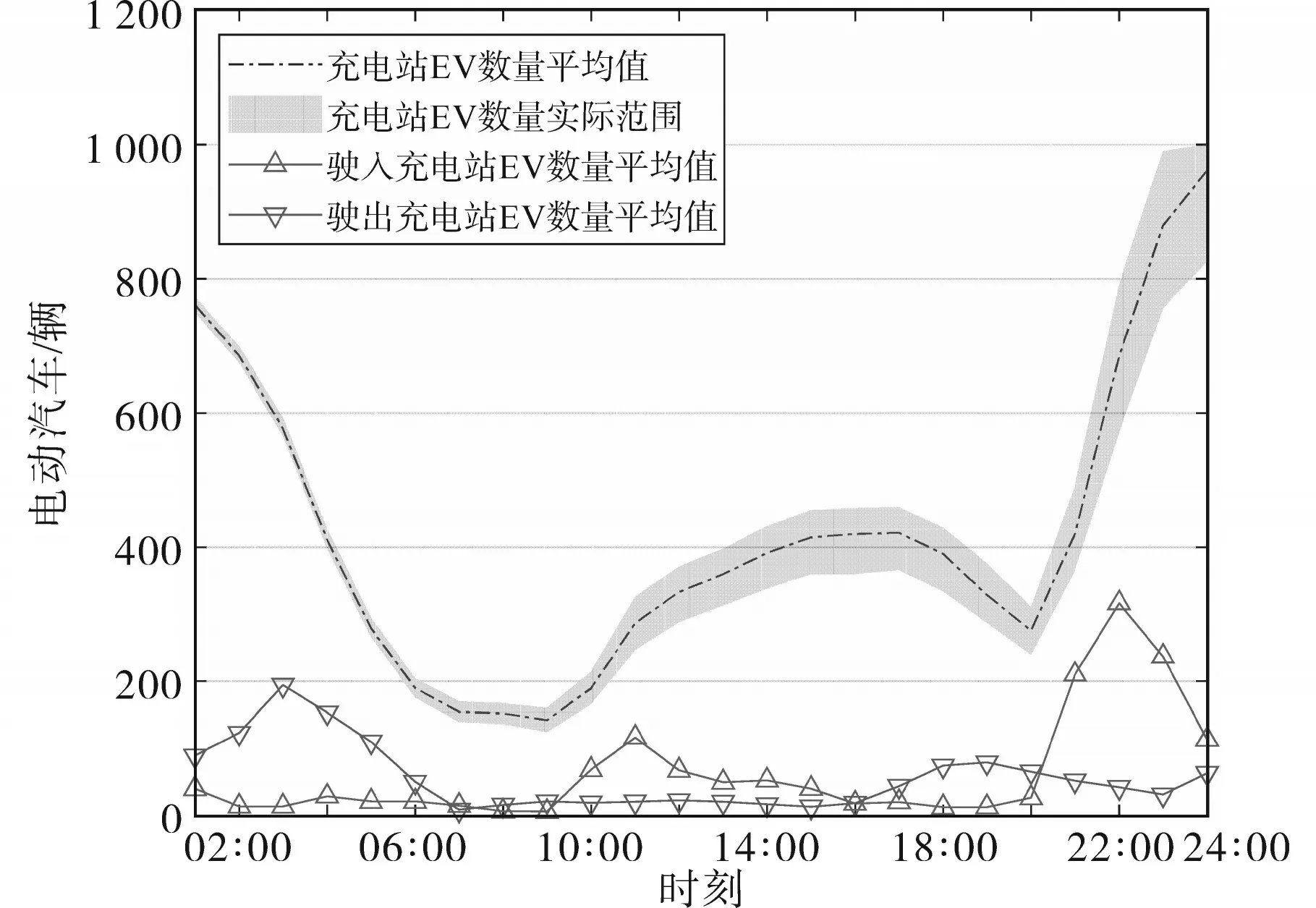
图3 电动汽车数量曲线Fig.3 Electric vehicle volume curves

设置风电额定总有功出力为3 MW；可控分布式机组发电总有功出力为10 MW，其余参数如表1 所示；储能容量1 MW·h，充、放电效率均为0.95；EV 充电站容纳电动汽车总数为1 000辆，单个电动汽车的电池容量为50 kW·h，电池最大充、放电功率为10 kW，充、放电效率均为0.95；EV 抵达充电站时的起始SOC 服从正态分布N（0.34，0.1），充电时间服从正态分布N（8.5，1）；风电出力预测误差标准差设为预测值的15%。

表1 虚拟发电厂分布式发电参数Tab.1 Unit operation data of VPP distributed energy resource

4.1 算法参数设置

为验证本文方法的有效性，分别采用DDPG，TD3，SAC 作为EV 充电站的强化学习算法，将TD3，SAC 作为VPP 的强化学习算法，形成6 个算例，各算例算法的设置如表2所示。

表2 各算例算法设置Tab.2 Algorithm settings for different cases

对于EV 充电站采用的算法，策略网络和价值网络的隐含层层数均为2 层，每层有128 个神经元，隐含层的激活函数均为Leaky ReLU（泄露修正线性单元），折扣因子为0.99，mini-batch 大小为128，缓冲记忆库大小为20 000，τ为0.001，采用Adam优化器更新网络权重。DDPG算法的价值网络学习率为0.001，策略网络学习率为0.000 1；TD3算法的价值网络学习率为0.001，策略网络学习率为0.001；SAC 算法的价值网络学习率为0.000 5，策略网络学习率为0.000 3。

对于VPP 采用的算法，策略网络和价值网络的隐含层层数均为2 层，每层有256 个神经元，TD3算法的价值网络学习率为0.000 1，策略网络学习率为0.000 2，其余参数与EV充电站的算法相同。

4.2 训练过程与收敛性

本文算法采用Python3.8 编写，采用Pytorch 1.6.0 作为深度学习框架。网络的参数更新使用CUDA 并行计算架构加速，并在NVIDIA GeForce GTX 1660 GPU 上执行；智能体与环境互动及其更新部分使用Numba[32]即时编译器技术加速。本文算法在Intel Core i7-8750H CPU @ 2.20GHz 和内存为8GB 的电脑上运行，每个完整的算例平均需要用69 min。

本文搭建的框架中，每小时计算一次回报，智能体的回报均为经济收益减去惩罚量。智能体根据获得的回报每小时对网络参数进行更新，则每24 h 的训练为1 幕（eposide）。设置EV 充电站智能体的训练幕数为450，VPP 智能体的训练幕数为7 350，EV 充电站与VPP 平均每幕的回报如图4和图5所示。

图4 EV充电站智能体训练过程的回报Fig.4 Rewards of the EV charging station agent training process

图5 VPP智能体训练过程的回报Fig.5 Rewards of the VPP agent training process

训练过程中VPP 向EV 售电价格的迭代收敛情况如图6所示。

图6 VPP向EV售电价格迭代收敛情况Fig.6 Iterative convergence of VPP to EV power sales prices

从图4～图6 可以看出，EV 智能体能在100幕后逐渐收敛，VPP 智能体能够在4 000 幕左右逐渐收敛，并在之后缓慢优化。VPP 向EV 售电价格随迭代的进行能够逐渐收敛。训练过程中收益的波动则主要受随机量影响。从训练过程来看，DDPG 算法的稳定性和成功率不如TD3 和SAC。从奖励数值来看，VPP 采用SAC 算法时获得的奖励更高。

4.3 强化学习优化调度结果分析

以TD3 作为EV 充电站的智能体训练算法，以SAC 作为VPP 的智能体训练算法，利用历史数据对智能体进行离线训练，其计算收敛后得到的调度结果如图7所示。

图7 交易功率和调度结果Fig.7 Trading power and scheduling results

由图7可以看出，储能在电价的引导下充、放电，在00：00—18：00 的低电价时段充电，而在18：00—24：00 的高电价时段放电。燃气轮机在低电价时段发电少，在高电价时段前提前提高发电功率，并在高电价时段以额定功率发电。VPP制定的EV充电价格结果如图8所示。

图8 EV充电站分时价格曲线Fig.8 Price curves of EV time-sharing charging

由图8 可以看出，由于式（23）的约束，VPP 制定的EV 充电价格始终在上、下限之间波动。EV充电站会根据价格信号改变用电行为，实现负荷削峰填谷并提高了供电可靠性，有利于VPP 的长期稳定运营。

4.4 算法类型的影响

在线调度阶段，采用蒙特卡洛法计算VPP 收益，分别用两种方案确定日前购售电量。

方案1：采用整个训练过程中，日前电力市场购售电量PDt的滑动平均值作为向ISO 申报的实际购售电量。

方案2：采用整个训练过程中，日前电力市场购售电量减去实时平衡市场购售电量，即PDt-PRt的滑动平均值作为向ISO申报的实际购售电量。

在智能体训练完成后，采用蒙特卡洛方法模拟调度100 d，并取平均值作为收益结果。模型采用不同算法求解的结果如表3所示。从结果看出，在本文建立的VPP 与EV 充电站主从博弈模型中，当VPP 采用随机性策略时，其净收益更高，且惩罚更小；当EV 充电站采用确定性策略时，其成本更低。采用两种方法确定DAM 实际购售电量时，VPP 收益没有明显差异，这也能说明本文方法计算出的结果是较优的。

表3 各算例求解结果Tab.3 The results of solving each case

从实际训练过程来看，由于智能体的价值网络在起始时估值不准，DDPG 算法可能存在价值高估的问题并在迭代中不断恶化，导致训练过程崩溃。因此本文建议用TD3作为EV充电站的算法。

从结果来看，VPP 更倾向于采用基于随机性策略算法，即博弈论中的混合策略；而EV 充电站倾向于采用确定性策略算法，即纯策略。这是由于VPP 占据主从博弈中的主体地位，而EV 充电站占据从体地位。根据海萨尼的证明[33]，完全信息情况下的混合战略均衡可以解释为不完全信息情况下纯战略均衡的极限。在不了解EV 充电站支付矩阵的情况下，VPP 不能确定EV 充电站将选择什么样的纯策略。根据海萨尼转换，这种不确定性等价于VPP 不确定EV 充电站的具体类型。然而，对于占据从体地位的EV 充电站，其参与的博弈是完全信息的，因此采用纯策略更优。

4.5 博弈的影响

为研究博弈对模型均衡解的影响，将VPP 智能体的训练幕数设置为6 150，EV 充电站智能体的训练幕数设置为450。在采用博弈模型时，采用3.2 节流程交替训练主、从智能体。在不采用博弈模型时，则先训练完成VPP 智能体，再训练EV充电站智能体。

采用方案1 确定日前购售电量，分别计算在主从博弈和不采用主从博弈模型下的收益，如表4、表5所示。

表4 采用VPP主从博弈模型VPP收益与EV成本Tab.4 VPP benefits and EV costs using VPP Stackelberg game model

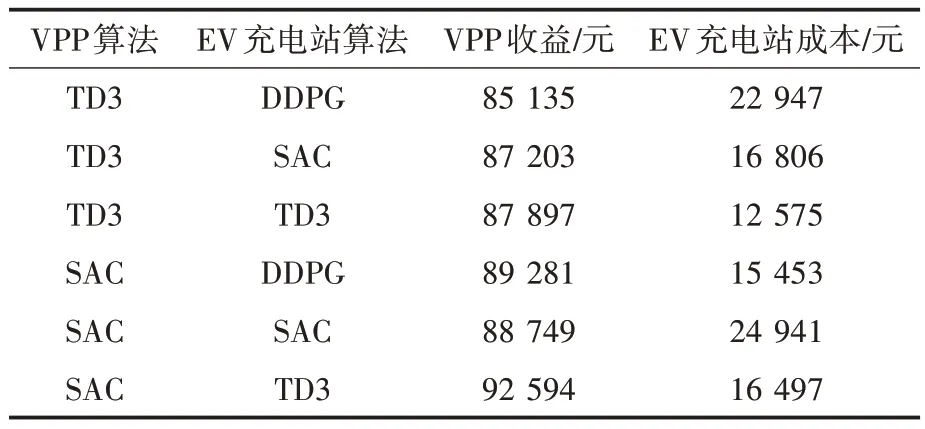
表5 不采用VPP主从博弈模型VPP收益与EV成本Tab.5 VPP benefits and EV costs without using VPP Stackelberg game model

从表中计算结果看出，主从博弈降低了EV充电站的成本，同时降低了VPP 的总收益，这是由于VPP 的部分收入来自于EV 充电站支付的电费。虽然VPP 的目标为收益最大化，但由于与EV 充电站存在博弈，限制VPP 过度榨取收益，使其只能获取相对最优的收益，且总体下降。本文建立的模型不仅能降低EV 用户成本，且实现了全社会成本下降。

5 结论

本文针对电动汽车虚拟电厂调度问题，提出以SAC 和TD3 算法训练得到智能体并以此进行VPP 和EV 充电站调度，通过算例验证了方法的有效性，所得结论如下：

1）本文提出的虚拟电厂智能体能够学习向EV 售电价格策略，对内部资源优化调度，参与电力市场交易；电动汽车聚合代理商智能体能够学习EV充、放电调度策略。

2）基于TD3 强化学习方法能够对VPP 内EV充电站调度进行优化控制，在电动汽车数量较多的情况下能够有效计算。

3）主从博弈降低了EV 充电站的成本，也降低了VPP 的总收益，这表明该算法可以限制VPP的过度榨取收益，使全社会成本降低。