基于分段二次流变模型的泥石流流速垂向分布
杜 翠,李 戎,梁 斌
(1.成都信息工程大学 软件工程学院,四川 成都 610225;2.河南科技大学 土木建筑学院,河南 洛阳 471023)
0 引言
泥石流流速垂向分布特征关系到泥石流流量、平均流速、运动阻力、冲击力等重要参量的计算,是泥石流运动理论模型研究的核心问题之一[1-2]。目前,关于泥石流流速多按照表面流速、龙头平均流速来计算,主要依靠经验、半经验的方法确定[3-5],且假设泥石流断面流速均一。实际上,泥石流属于非牛顿流体,其流速分布在整个流深范围以及在断面横向范围内是不均一的。
国内外针对泥石流的垂向流速分布开展了较多研究。文献[6]基于广义的粘塑性流体模型,推导了恒定均匀流条件下泥石流剖面垂直方向上的速度分布公式。文献[7]基于泥石流的结构两相流模型,分别讨论了泥流及水石流流速的垂向分布特征。文献[8]将泥石流体简化为具有相同粒径的固相和具有相同力学性质的液相,运用两相流理论建立了泥石流固液分项流速控制方程,求解得到了固液分相流速计算方法。文献[9]基于非均质泥石流固液两相分界粒径的概念,以达西(Darcy)公式和质量守恒定律为理论基础,分别推求了非均质泥石流的固液两相平均流速表达式。文献[10]基于守恒方程和膨胀体模型,推导了非恒定条件下的泥石流流速分布公式。文献[11]基于膨胀体模型推导的流速计算公式适用于缺乏细颗粒的饱和水石流。
文献[12]基于固液两相流模型建立了泥石流流速垂向分布模型,把泥石流分为固相和液相两种进行研究,未考虑泥石流中黏粒含量的影响。文献[13]用粒子图像测速技术测量玻璃珠在丙烯酸树脂和乙酸乙酯混合液中的速度场,研究了稀性泥石流的流速分布。此类研究中所用透明介质均为牛顿体,泥石流中的泥浆具有较大的屈服应力,因此该研究适用于细颗粒含量较低的水石流和稀性泥石流,不适合粘性泥石流模拟。
泥石流的运动取决于泥沙浓度、颗粒组成、流深和沟道坡度,不同类型的泥石流主应力不同。最常用的流变模型有摩擦流变模型[14]、Voellmy流变模型[15]、Coulomb-viscous-based流变模型[16]和二次流变模型[17]。从理论上讲,二次流变模型涵盖了不同流态下的主应力(屈服应力、粘性、碰撞和湍流应力)[17],更能说明泥石流运动的动力学过程,在此基础上得到的泥石流流速垂向分布更合理。本文基于泥石流二次流变模型,先进行分段处理,再通过积分计算给出泥石流流速垂向分布计算公式,利用泥石流试验数据对比分析抛物型流变模型(数值解)、分段流变模型和Arai-Takahashi模型。在此基础上,给出以上3种模型中卡门常数κ与含沙量Cv,泥石流垂向流速为0的位置y0与代表粒径D、含沙量Cv的经验关系。
1 泥石流流速分布
1.1 泥石流二次流变模型
泥石流是介于滑坡和高含沙水流之间的特殊流体,兼具有滑坡不具有的流动性和高含沙水流的结构性。对于粘性泥石流,龙头强烈紊动,而龙身和龙尾紊动强度弱,其剪应力主要由屈服应力和粘性剪切应力组成;对于水石流,由于细颗粒含量少,浆体粘度低,粘性剪切应力较小,其剪应力主要由紊流应力和颗粒碰撞应力构成。为了能够包含不同类型泥石流的应力组成,泥石流或泥流的剪应力二次流变模型为[17]:
(1)
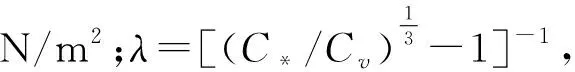
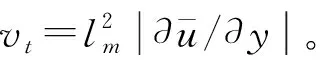
抛物型粘度模型[20]:
(2)
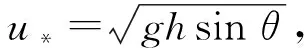
将式(2)代入式(1),得:
(3)
求解得:
(4)
1.2 泥石流流速分布公式
当屈服应力存在时,流体呈现两层流动,即塞流层(流速梯度为0)和剪切层(流速梯度不为0),如图1所示。
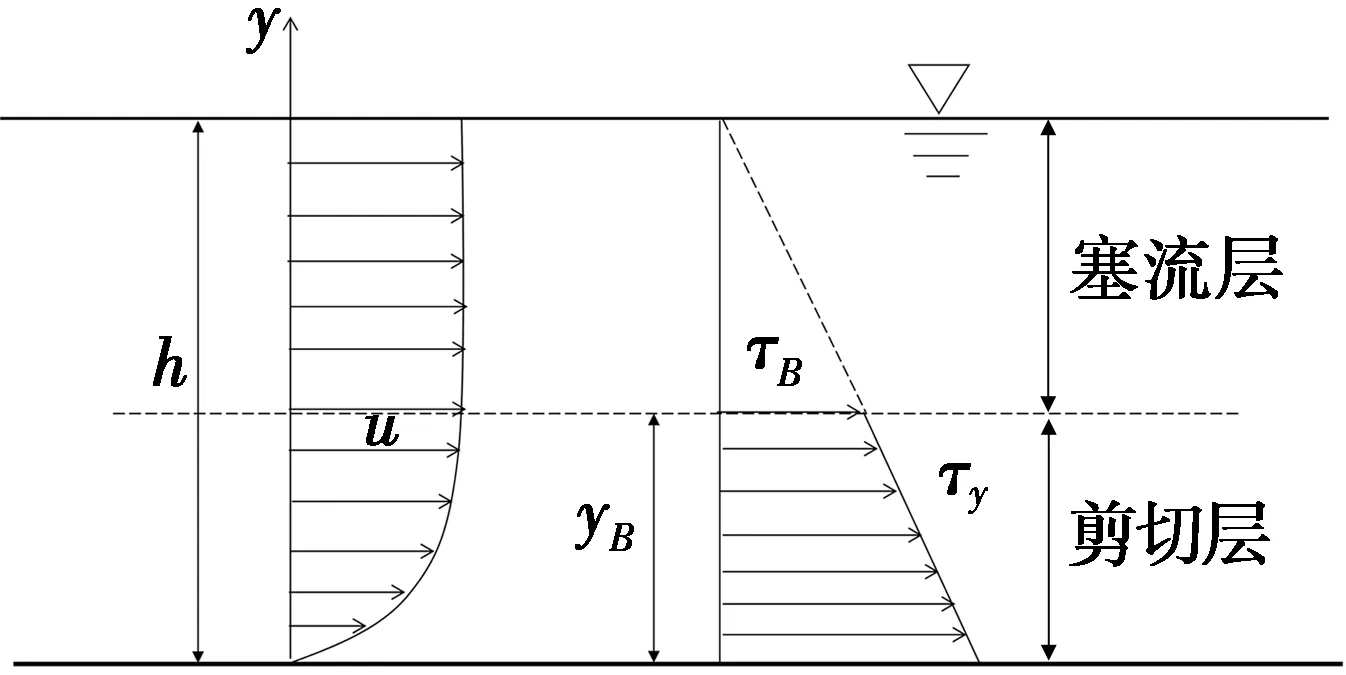
图1 塞流层示意图
在剪切层y=yB,τ=τB,剪切层厚度计算方程为
(5)
上层剪切应力小于屈服应力没有相对运动假设为刚性层;底层剪应力大于屈服应力,形成速度梯度,紊动粘度通常是用抛物线模型确定:
(6)
为了给出方程(4)的解析解,方程(6)分段函数如下,
(7)
如果y∈[0,yB/2],νt=κu*y/2,则
(8)
如果y∈[yB/2,yB],νt=-κu*(y-yB)/2,则
(9)
方程(8)在边界条件y=y0,u=0积分得,
(10)
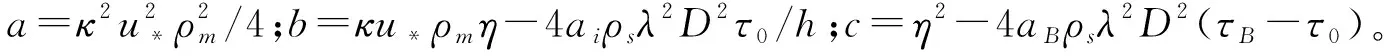
对方程(9)进行积分得:
(11)
(12)

1.3 Arai-Takahashi模型
不考虑屈服应力τB和粘性剪切力ηdu/dy,方程(1)为:
(13)
文献[21]根据普朗特(Prandtl)边界层理论lm=κy,
(14)
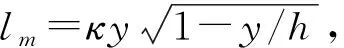
2 计算结果与测量流速分布对比
2.1 试验数据
本文利用17组数据对比分析抛物型粘度模型、分段粘度模型、Arai-Takahashi模型,验证分段粘度模型的适用性。试验数据分别来自文献[21]、文献[22]、文献 [11]和文献[23]。文献[21]、文献[22]和文献[11]试验考虑了无粘性颗粒流、粘性流体和玻璃珠,文献[23]考虑粘性颗粒的泥石流,试验参数如下表1。

表1 试验参数
2.2 计算值和试验数据分析
依据表2中的试验参数,分别计算抛物型粘度模型、分段粘度模型、Arai-Takahashi模型,抛物型粘度模型[式(4)]采用数值计算,分段粘度模型[式(10)和式(11)]和Arai-Takahashi模型[式(14)]是积分计算,得出计算结果,对上述17个案例分别进行了计算。图2为对颗粒流、粘性泥石流、以玻璃珠和水为试验材料的泥石流的结果展示。
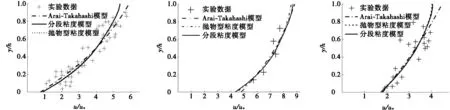
(a) 颗粒流 (b) 粘性泥石流 (c) 玻璃珠和水
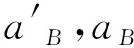
总体而言,与Arai-Takahashi模型相比,本文提出的分段粘度模型结果与抛物型模型结果比较接近。由于在Arai-Takahashi模型中,没有考虑屈服应力和粘性剪切应力,所以其流速梯度曲线无法得出塞流层,从而导致过估泥石流体表层的流速值。且Arai-Takahashi在颗粒流表层流速计算结果过估程度超过了粘性泥石流。
2.3 κ和y0的计算公式
根据前述的3种泥石流类型的拟合结果中可以得出泥石流底部流速不为0。由于每组试验数据中的y0、卡门常数κ是泥沙含量Cv变量,通过对案例1~案例17进行计算得出卡门常数κ和y0的值如表2,通过拟合得出y0值、卡门常数κ与泥沙含量Cv变量的关系(图3和图4)。

(a) Arai-Takahashi模型 (b) 分段粘度模型 (c) 抛物型粘度模型

(a) Arai-Takahashi模型 (b) 分段粘度模型 (c) 抛物型粘度模型
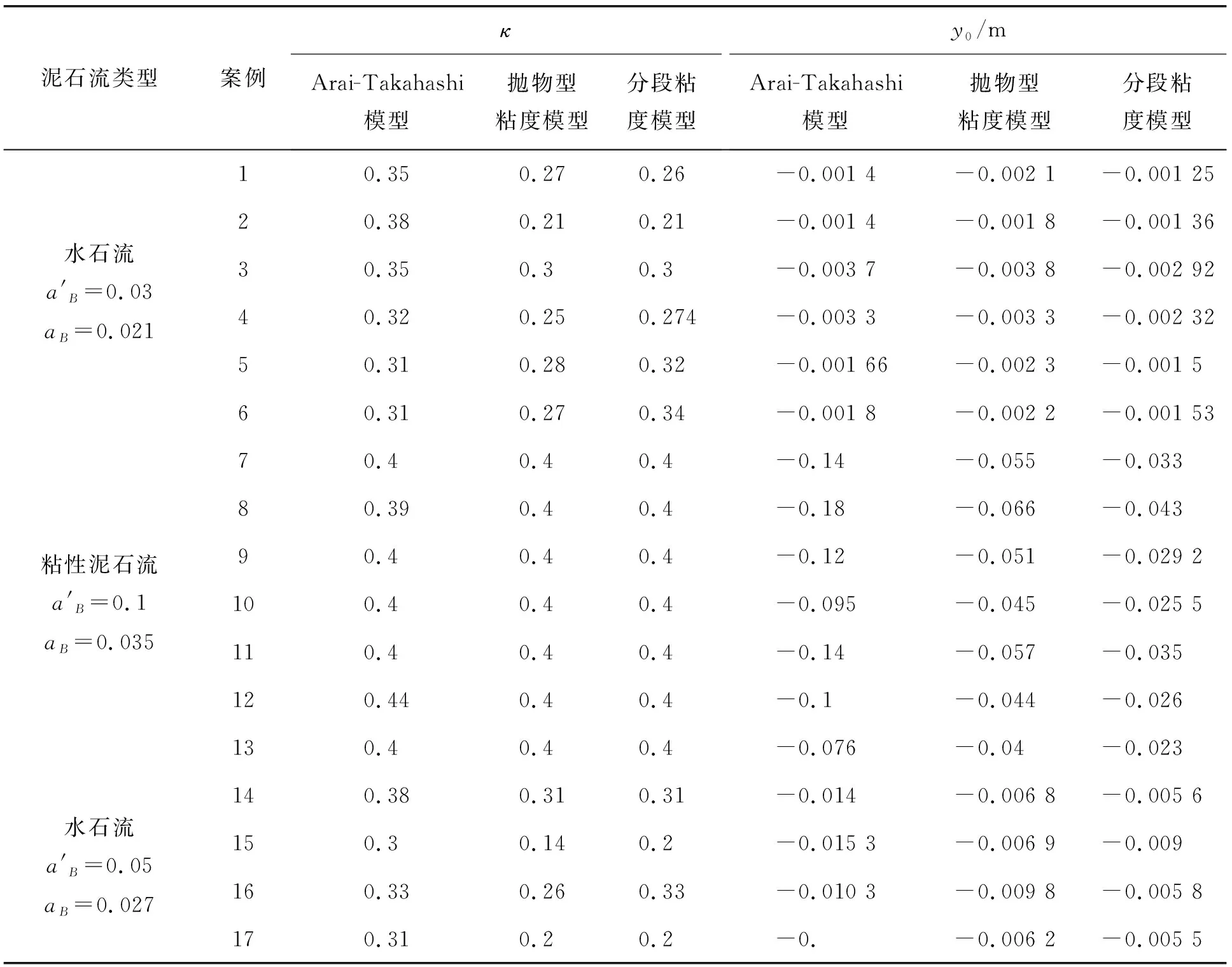
表2 κ和y0的值
图3给出了Arai-Takahashi模型、分段粘度模型和抛物型粘度模型这3种计算模型的卡门常数κ与含沙量Cv之间的关系,在实际计算中根据测得Cv值计算κ。该关系与含沙水流结果相似,在清水条件下,卡门常数κ为0.4,并随着含沙量的增加先降低后升高。
图4给出了流速为0时,y0/d与含沙量Cv之间关系,其满足幂律分布。在高含沙水流中,y0=ks/30,ks是河床粗糙层厚度。对于光滑河床,y0=0.11ν/u*,其中,ν是水的运动粘度,u*是河床剪切速度。在泥石流运动过程中由于粗糙面和泥石流运动过程的紊动过程,在运动中掺杂气体,在泥石流底部不能无线斜坡光滑模型,在泥石流速度为时,y0不为0。
3 结论与讨论
泥石流垂向流速梯度是泥石流动力学研究中的核心问题之一。考虑到泥石流剪切应力组成的多重性,二次流变模型较为全面地涵盖了屈服应力、粘性剪切应力、紊流应力和颗粒离散应力。对于粘性泥石流而言,由于紊流应力和颗粒离散应力远小于粘性剪切应力,因此二次流变模型可以近似为粘塑性模型。Arai-Takahashi模型基于Bagnold 的膨胀体模型推导了水石流流速垂向分布遵循的幂律关系,不包含屈服应力和粘性项。本研究将紊动粘度模型分段化,进而给出解析解,建立分段粘度模型,获得垂向流速分布,给出垂向流速计算表达式。
利用17个定床试验数据验证了分段粘度模型、Arai-Takahashi模型以及抛物型粘度模型与试验数据吻合程度,结果表明:分段粘度模型与抛物型粘度模型吻合度较高。同时,本文给出了卡门常数与泥沙含量之间的拟合关系,根据含沙量估算卡门常数的值,给出了泥石流流速为0的深度参数y0与中值粒径D和含沙量Cv的关系,根据中值粒径和含沙量可大致估算泥石流侵蚀深度。
本文中根据分段粘度模型进行泥石流流速计算可以估算泥石流断面流速,但是计算过程稍显复杂,下一步将寻找相对简单的计算方法或建立简单的数学计算模型;本文泥石流为饱和泥石流,对于非饱和泥石流,流速呈“反S”曲线,该流速计算模型不适用;由于缺乏动床试验数据,本文没有对此进行分析,后面会继续开展动床方面的研究,对理论进行补充。

