基于用户画像与Stackelberg 博弈的交通环岛通行策略
曹栋发,李 勇,胡创业,丁 男,2
(1.新疆师范大学 计算机科学技术学院,乌鲁木齐 830054;2.大连理工大学 工业装备智能控制与优化教育部重点实验室,辽宁 大连 116024)
0 概述
交通环岛是城市交通中必不可少的交通场景之一,其目的是替代交通信号灯,让不同行驶方向的车辆安全通行[1],以提升交通通行效率。然而,随着路网中车辆数量不断增加,环岛通行效率降低[2],拥堵现象频发。受环岛道路场景限制[3],交通环岛入口与出口处的通行压力日益增大,车辆驶入环岛与驶出环岛的冲突加大,甚至出现交通事故。因此,交通环岛的通行已逐渐成为城市交通亟待解决的问题。智能网联汽车[4]利用网络以及人工智能,实现车-路-环境协同,辅助驾驶进而提升车辆行驶安全性与舒适性,已成为新一代智能交通系统中有效解决交通拥堵方案之一。基于交通环岛通行规则以及场景特点,结合智能网联汽车人-车-路-环境协同[5],车辆在驶入环岛和驶出环岛时换道策略以及通行策略的研究能有效提升交通环岛通行效率与安全,逐渐成为一种有效的解决途径。
研究人员结合交通环岛通行场景,利用智能网联汽车协同提升车辆通行效率,设计相邻车辆间通行策略。目前,相关研究主要集中在车辆跟驰决策控制、车辆换道研究以及车队编队控制。例如,通过基于联盟博弈论的协同编队[6]、主动车辆和被动车辆之间的马尔可夫博弈[7]、基于合作博弈的全局最优合并模型等方法优化协同策略性能[8]。同时,对于环岛中的车辆博弈,研究人员采用Stackelberg 博弈(STG)和大联盟博弈相结合的方法[9],构建车辆之间相互作用与驾驶员类型的博弈模型[10],还有基于重复博弈论和子博弈中求解纳什均衡解的方法生成有效且高效的路线规划[11]。然而,协同策略设计主要基于车辆行驶的速度、距离等基础数据[12]并假定车辆可以实时通信。因此,在实际应用中通信受限情况下,结合交通环岛特点,利用智能网联汽车系统中其他辅助信息[13-14]设计的协同策略还需进一步研究。
随着智能网联汽车中感知技术以及网络技术的不断发展,其系统中数据混杂多样已成为趋势。虽然相关行业标准与白皮书已对系统中车、路、环境等相关数据进行描述和定义,但是数据类型的多态混杂是不可避免的,例如,离散数据与连续数据混杂、周期性数据与非周期性数据采集混合等。用户画像作为一种能够统筹异构数据、表征动作倾向和意图的行为模型,逐渐应用于智能网联汽车的相关研究。研究人员利用用户画像对智能网联汽车系统中异构多维数据进行组织与表征[15-16],进一步提升交通环岛中车辆换道以及通行策略的性能。同时,结合预测技术,弥补系统中小样本数据或者无法直接采集的信息缺失,进一步完善用户画像对协同策略的知识表征和数据支撑。
在智能网联汽车系统中实时通信受限的条件下,本文提出交通环岛中车辆换道以及车辆驶入和驶出时车辆协同通行策略。在环岛中心设置路侧单元(Road Side Unit,RSU),车辆可以获取到自身以及周围车辆、环境等历史信息。基于时空特征的车辆预测方法AP-LSTM,通过关联规则对智能网联汽车中的多维异构数据进行分析,以提高预测精度。同时,结合车辆画像,在车辆轨迹预测的基础上设计强制换道策略。
1 基于车辆画像的场景数据处理
在智能网联汽车的发展阶段,车辆上拥有众多车载智能设备来获取车辆数据,包括传感器、处理器、通信设备等。因此,本文以车辆作为边缘节点,通过车辆进行数据感知,并通过地理位置更靠近边缘节点的RSU 协作处理车联网感知数据,以提高多车协同的车联网整体计算效率,提升多车协同感知的信息融合性能。环岛场景示意图如图1 所示。本文在环岛路口处设立4 个RSU,通过RSU 对路口处车辆感知数据进行统筹处理后,由RSU 将数据分发至各边缘节点进行存储和计算。
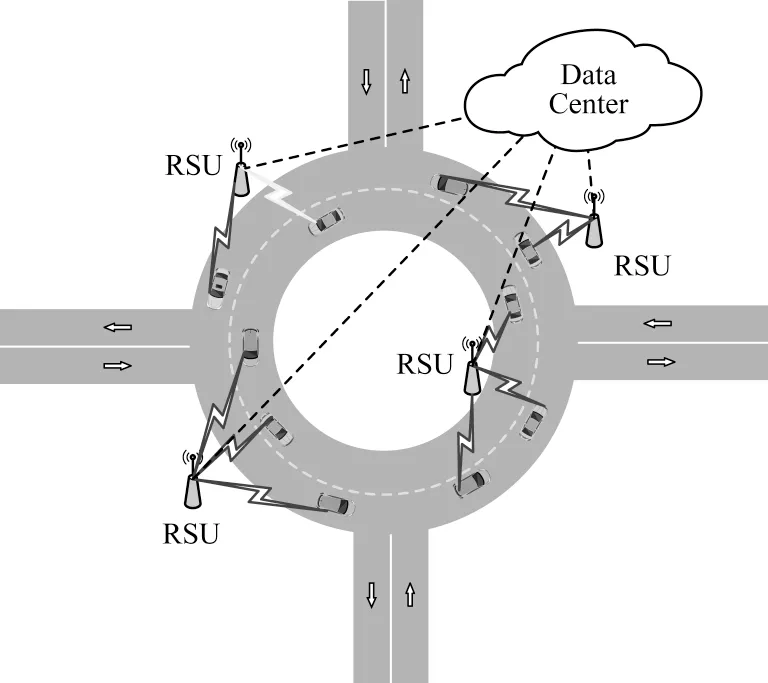
图1 环岛场景示意图Fig.1 Schematic diagram of roundabout scene
车联网数据不仅包含其本身的实时位置、速度等连续数据,还存在控制车辆的制动程度、转向程度等驾驶动作的离散数据。同时,车联网数据在从传统车联网狭义概念到智能网联汽车广义概念的发展过程中,不再局限于少量的终端数据。在自动驾驶白皮书中所提到智能网联汽车的车辆数据不仅包括汽车基础数据,也包括基础设施、外界环境、交通数据(道路车道规模、周围车辆的具体位置、行驶和运动方向、天气状况、车流密集程度),以及车主的身份数据(驾龄、年龄)、状态数据(手势、眼球位置变化等)、行为数据(异常变道频率、驾驶风格等)。
由于智能网联汽车融合了来自汽车、道路、天气、用户等多方面的海量数据,因此导致智能网联汽车数据呈现多维度、规模大的特点。同时数据的多维度决定了不同来源的数据格式不同,使得数据存在非结构性和非标准性问题。因此,本文引入车辆画像对多维度的智能网联汽车异构数据进行表征。
本文收集不同区域环境下驾驶员信息、车辆信息、车辆运行状态、驾驶行为、外界环境5 个维度的经验数据。图2 所示为在这5 维数据中包含驾龄、车辆类型、车间距、速度、加速度变化、异常变道次数、交通流状况等特征的车辆画像。按照相关交规以及其他划分标准,将这5 维数据中包含的特征划分成不同的特征类型。其中,驾驶员信息和车辆信息为固有信息,车辆运行状态可通过车载传感器获取,外界环境数据经由RSU 采集后分发给各节点,而驾驶行为可以通过视觉协同分析等方法得到,以构建出的车辆画像能够准确捕捉驾驶过程中的动态特征,从而解决智能网联汽车传输数据混杂、数据维度多的问题,提升数据分析效用。

图2 车辆画像示意图Fig.2 Schematic diagram of the vehicle portrait
2 轨迹预测
本文基于构建的车辆画像捕捉车辆在不同区域环境下的潜在特征,优化在驾驶过程中受场景的时变和多样性因素导致小样本数据预测难度增大,以提高车辆轨迹预测的准确性和实时性。
为实现基于小样本特性的车辆轨迹预测,本文在车辆画像的基础上,开发了AP-LSTM 算法,挖掘不同时空状态下最具代表性的车辆画像标签,降低数据维度,用于车辆轨迹预测,以此作为后续车辆协同博弈的基础。同时,由于长短时记忆(Long Short-Term Memory,LSTM)网络在车辆轨迹预测方面很难兼顾数据量、算法实时性和预测准确性,无法实现长时且实时预测,因此在预测结果基础上,通过卡尔曼滤波算法对超过3 s 的长时预测结果进行降噪优化。
2.1 基于Apriori 的关联规则分析
Apriori 算法[17]是研究关联规则的经典方法,用于扫描数据集中满足最小支持度minsup 的频繁项集和提取频繁项集中满足最小置信度minconf 的关联规则,可以独立挖掘数据集中的关联规则,适用于小数据集的关联规则分析。本文通过Apriori 算法实现如下应用。
假定车辆驾驶特征集为A,如式(1)所示:
其中:行式为特征在不同时间下的特征类型;列式为在同一时间下的不同特征。环岛场景为B,B=(b1,b2,b3)为环岛出入口等的不同场景。
关联规则的支持度Support 为项集中所有项同时发生的概率,A和B的支持度如式(2)所示:
式(2)表明在环岛场景中各项车辆驾驶特征同时出现的概率。置信度Confidence 表明各项驾驶特征在不同场景下产生的条件概率,A和B的置信度如式(3)所示:
提升度Lift 用于表明不同驾驶特征与不同场景之间的倾向性,A和B的提升度如式(4)所示:
若LAB>1,表 明A和B正相关,A、B关联规 则有效。
定义1(强关联时空特征)强关联规则X⇒Y表示要挖掘的关联规则,同时满足以下2 个条件:
2.2 AP-LSTM 预测
长短时记忆是递归神经网络(Recursive Neural Network,RNN)的一个变种,构建了专门的记忆存储单元,通过时间反向传播算法训练数据,以解决RNN 网络存在的梯度消失及无长期依赖的问题[18]。LSTM 网络包括遗忘门、输入门和输出门3个控制门,3类门共同控制信息的输入和输出,具体结构如图3 所示。LSTM 的门结构使得时间序列上的信息形成一个平衡的长短期依赖关系,适用于交通流时间序列的信息提取。

图3 长短时记忆网络结构Fig.3 Structure of long short-term memory network
对于车辆轨迹预测,智能网联汽车的多维异构数据维度的增加意味着预测实时性降低,数据维度的减少在一定程度上表示预测准确性降低。为此,本文结合车辆画像,通过AP-LSTM 算法来捕捉车辆行驶特征,实现预测实时性和预测准确性的平衡。
因此,本文选取由Apriori 算法组合的具有强关联性的多类型驾驶数据作为输入序列[x1,x2,…,xt],W、b分别为每个计算值的权重矩阵和偏置项,C^t为当前输入作用下的单元状态,ht-1为上一时刻的隐藏层输入,⊙表示两向量按元素的乘积,tanh 为非线性激活函数。LSTM 的单元经过这样处理后就得到了更新后当前时刻的单元状态Ct和隐藏层值ht,最后根据实际需求设置隐藏层与输出层的连接即可。
为了降低长时预测的误差,本文通过卡尔曼滤波算法对超出3 s 的LSTM 长时预测结果进行优化。
卡尔曼滤波器分为预测阶段和更新阶段。在预测阶段,卡尔曼滤波器使用上一状态的估计对当前状态进行估计。在更新阶段,滤波器通过预测出的状态值对系统进行更新。卡尔曼滤波器预测阶段和更新阶段的状态方程如式(7)和式(8)所示:
基于以上内容和定义,AP-LSTM 算法主要由3 个部分组成,即强关联性特征的生成、LSTM 轨迹预测、长时输出的卡尔曼滤波优化,具体结构如图4所示。有关详细信息见算法1。

图4 AP-LSTM 框架Fig.4 AP-LSTM framework
算法1AP-LSTM 算法
步骤1获取当前车辆历史行驶数据,构建车辆画像。
步骤2基于车辆画像计算候选集支持度,并根据指定的最小支持度构建频繁项集。
步骤3提取频繁项集中满足最小置信度的关联规则。
步骤4根据获取的关联规则,基于相关特征进行数据输入,实现LSTM 轨迹预测。
电网电压骤降恢复对双馈风电机组连锁脱网的影响//周步祥,董申,林楠,刘舒畅,张冰,赵磊//(17):34
步骤5基于LSTM 的轨迹预测序列,通过卡尔曼滤波算法对其中超出3 s 的长时部分生成最终输出序列。
步骤6重复步骤1,直至所有车辆运行完毕。
3 换道博弈策略
为解决在通信受限情况下的换道感知和决策问题,同时为了降低数据误差对换道决策性能的影响,本文结合车辆历史数据,通过AP-LSTM 算法对车辆状态进行估计和预测,基于预测轨迹对处于环岛出口处的车辆进行换道博弈。首先定义了领导者和跟随者收益函数,然后基于收益函数给出Stackelberg 博弈策略,最后对Stackelberg 均衡点进行验证。
3.1 换道场景
一般情况下,车辆的换道行为只涉及换道车辆与其周边车辆。因此,本文将换道问题简化为图5所示的场景。SV 和SRV 分别作为目标车辆和邻居车辆,LV 和PV 作为SV 和SRV 的前车。因此,车辆换道问题可以抽象为在保证安全性和平稳性的前提下,结合AP-LSTM 算法预测的SV 和SRV 车辆轨迹,确定SV 的后续驾驶行为,使得SV 在到达出口前换道至外侧车道。
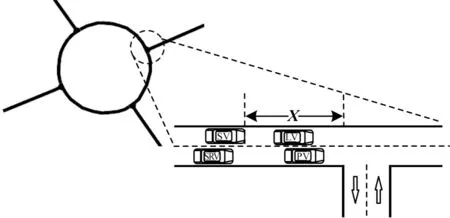
图5 换道场景示意图Fig.5 Schematic diagram of the lane-changing scene
3.2 Stackelberg 博弈
Stackelberg 博弈是经济学中的一种战略博弈,领导者先行动,追随者后行动,追随者按领导者的策略行动。因此,领导者需要考虑追随者在选择策略时的最优响应[19]。由于车辆换道过程是以换道车辆SV 首先开启转向动作为开端,邻居车辆SRV 才根据周围状况确定下一步动作,两者之间存在一定的顺序,因此本文将车辆换道问题建模为SV 与SRV 之间的Stackelberg 博弈。
文献[20]通过对博弈双方车辆距离变化来衡量驾驶员的驾驶风格,大于安全距离表明驾驶风格保守,而距离越小,表明驾驶风格越激进。结合此方法,本文设定如下驾驶行为识别参数来表述驾驶风格。
定义2驾驶行为识别参数如式(10)所示:
领导者收益函数如式(11)所示:
收益函数主要由3 部分组成:第1 部分PvUv(sv)和Uv(srv)描述了车辆SV 和SRV 的安全性收益,考虑到两辆车相对速度差越大,其驾驶距离差会随之增大,则安全收益越高;第2 部分Uacc(sv)和Uacc(srv)描述了SV和SRV 的舒适性收益,在驾驶过程中加速度变化越小,驾驶越平稳,舒适性收益越高;第3 部分Upos(sv)和Usp(k)描述了车辆的激进性收益,对于车辆SV,随着距离出口越近,越急于换道,其驾驶的激进性越高,对于SRV,基于前后车距的驾驶行为识别系数表明了其激进性收益。
换道车辆SV 基于Stackelberg 博弈求解采取换道动作的时刻N′以及换道时刻车辆需要采取的速度,邻居车辆SRV 求解针对SV 换道行为所需的速度。其中,vsv(k)、vsrv(k)为车辆SV 和SRV在未来N步预测轨迹中获取到k时刻的速度,asv(k)、asrv(k)为车辆SV 和SRV 在未来N步预测轨迹中获取到的k时刻加速度。具体的求解过程如算法2所示。
算法2STG 算法

3.3 PMC 算法
3.3.1 算法设计
算法3 给出PMC 算法运行的整体框架,通过车联网获取行驶至环岛出口前的车辆数据,由此构建车辆画像来提取关联规则,实现基于关联规则的轨迹预测,最终通过轨迹预测结果进行Stackelberg 博弈,求解车辆在环岛出口处所需采取的动作。
算法3PMC 算法
步骤1获取当前车辆历史行驶数据,构建车辆画像。
步骤2基于车辆画像构建频繁项集并提取满足minconf 的关联规则。
步骤3根据获取的关联规则,基于相关特征进行数据输入,实现LSTM 轨迹预测。
步骤4
步骤5重复步骤1,直至所有车辆运行完毕。
3.3.2 Stackelberg 均衡点分析
Stackelberg 均衡点分析见引理1。
引理1若是Stackelberg 博弈的Stackelberg 均衡点,则需满足以下条件[21]:
令式(23)等于0,可解得:
4 实验分析
4.1 实验场景描述
本文实验通过SUMO 平台进行性能验证。环岛整体场景的参数设定如表1 所示,其中,车辆的路径规划部分由SUMO 内置功能处理,PMC 仅在车辆到达换道位置(距出口150 m)时才接管。

表1 相关实验参数 Table 1 Relevant experimental parameters
为充分分析本文所提算法和策略的性能,本文从以下3 个方面进行性能分析:1)针对车辆画像中轨迹预测性能分析,将本文所提AP-LSTM 与主流的LSTM[22]和GPR[23]进行对比分析;2)针对交通环岛中稀疏、中度拥堵、严重拥堵等不同交通流密度场景,将本文所提PMC 与No-Predict[24]和SUMO原有算法[25]进行对比;3)针对交通环岛中车辆行驶冲突的关键出口处车辆通行性能分析,将本文所提PMC与Stackelberg、Nash[26]和SUMO 原有策 略进行对比分析。
4.2 轨迹预测分析
结合车辆画像,基于AP-LSTM 算法中满足minsup 和minconf 频繁项集的强相关特征如表2 所示,以E2、G3 作为LSTM 轨迹预测的输入特征,完成车辆的轨迹预测。

表2 频繁项集的强相关特征 Table 2 Strong correlation characteristics of frequent itemsets
为验证不同时空状态下车辆长时轨迹预测效果,以当前车辆为例,本文将车辆轨迹预测时长分别设为3 s、4 s、5 s 和6 s。采用均方根误差(Root Mean Square Error,RMSE)计算预测模型的误差。RMSE如式(27)所示:

图6 不同算法的均方根误差对比Fig.6 Root mean square error comparison among different algorithms
4.3 预测机制的协同性能优化分析
为分析在通信受限场景下PMC 算法中轨迹预测机制产生的优化效果,本文对PMC 算法、No-Predict 算法、SUMO 算法进行性能分析。不同算法在各场景下的车辆平均速度如表3 所示。不同算法在各场景下的速度和加速度标准差的优化表现如图7 所示。

表3 不同算法的车辆平均速度对比 Table 3 Average speed of vehicle comparison among different algorithms 单位:(m·s-1)
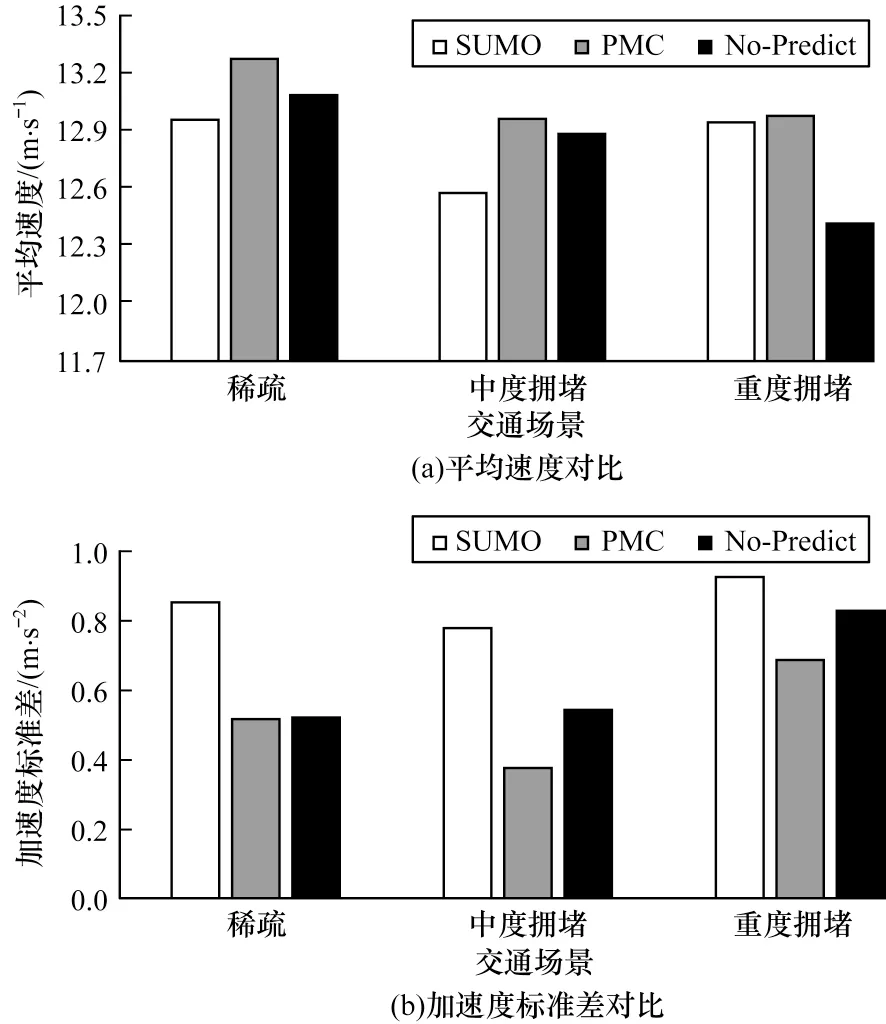
图7 车辆在不同预测机制下的平均速度和加速度对比Fig.7 Comparison of vehicle average speeds and vehicle accelerations under different prediction mechanisms
从图7(a)和表3 可以看出:在稀疏和中度拥堵交通场景下,虽然No-Predict 算法相较于SUMO 算法的平均速度有一定的提升,但是PMC 算法中基于预测状态的协同策略能够获得更快的平均速度。
在不同场景下,不同算法的加速度对比如表4所示。从图7(b)和表4 可以看出:在稀疏场景下,虽然PMC 算法的加速度标准差与No-Predict 算法相比降低的不明显,但是在其他场景下PMC 算法的加速度标准差均明显降低。图7 中加速度标准差越低,意味着车辆驾驶越平稳。因此,PMC 算法的驾驶平稳性效果在不同场景中均最优。

表4 不同算法的车辆加速度标准差对比 Table 4 Standard deviations of vehicle acceleration comparison among different algorithms 单位:(m·s-2)
在不同场景下,车辆在各预测机制下的加速度趋势如图8 所示。从图8(a)可以看出:PMC 算法在整体运行过程中虽然存在某一时刻的变化,但是其大部分时间相较于SUMO 和No-Predict 算法更加平稳。从图8(b)和图8(c)可以看出:PMC 算法的加速度波动均低于SUMO 和No-Predict 算法。

图8 车辆在各预测机制下的加速度趋势Fig.8 Acceleration trend of vehicles under various prediction mechanisms
因此,在通信场景受限的情况下,基于预测机制的协同策略(PMC 算法)相较于无预测机制的协同策略SUMO,在不同场景中均能够有效优化车辆通行效率与驾驶平稳性。
4.4 出口处实验分析
由于本文所提的基于预测机制的协同策略相较于无预测机制的协同策略性能优化效果已得到验证,因此本实验主要在通信受限场景下通过PMC 与SUMO、Nash、Stackelberg 算法进一步对比车辆通行效率和驾驶平稳性。其中,Nash 算法是对换道车辆及其周边车辆直接进行纳什均衡求解,Stackelberg算法则是以恒定加速度模型(即假定车辆速度)作为受限情况下的车辆状态估计,求解Stackelberg 博弈结果。出口处车辆的速度分布与加速度标准差分布情况如图9 所示。

图9 出口处不同算法性能分析Fig.9 Performance analysis among different algorithms at exit
从图9(a)可以看出:SUMO 算法存在某辆车的平均速度均快于PMC 和Nash 算法,但PMC 算法的最小值点、25%和50%分位点均高于SUMO、Nash和Stackelberg 算法,由此说明PMC 算法车辆通行效率的优化效果优于SUMO、Nash 和Stackelberg 算法。从图9(b)可以看出:PMC 算法加速度标准差的分布区间小于SUMO 算法,大于Nash 算法,并且PMC 算法的最小值点、25%和50%分位点、最大值点均低于SUMO 和Nash 算法,而Stackelberg 算法的最小值点、25%和75%的分位点以及最大值点均高于PMC 算法,由此说明PMC 算法具有较优的车辆平稳性。
5 结束语
本文提出一种基于用户画像与Stackelberg 博弈的交通环岛通行策略。通过构建车辆画像,在一定程度上解决智能网联汽车领域中多维异构数据的处理问题,有效表征车辆的时空状态。同时,结合构建的车辆画像,设计基于时空特征的车辆预测方法AP-LSTM,通过关联规则对智能网联汽车中的多维异构数据进行分析,以提高预测精度。在此基础上,结合Stackelberg 博弈对交通环岛路口处的车辆进行协同控制。实验结果表明,该策略能够有效提高环岛车辆的通行速度并确保驾驶安全性。下一步将结合真实车辆的协同控制,利用车辆传感器整合数据,以达到在现实场景下应用的目的。

