基于数据仓库的典型图查询处理技术

郭家鼎，王 鹏

（1.复旦大学 软件学院，上海 200438；2.复旦大学 计算机科学技术学院，上海 200438）

0 概述

随着数据量的增长和数据关联的日益复杂，图数据库系统逐步得到人们的关注［1］，并在知识图谱［2-3］、网络检测预警［4］、社交网络［5］、交通网络［6］、人工智能［7-8］等领域发挥越来越重要的作用。图数据可以简单理解为顶点、边和上面属性所组成的集合。现有的图查询一般涉及顶点和边上属性的查询、顶点或边之间的遍历以及属性结果的聚合、排序等操作。图遍历将实体间关联起来，因此也是图查询的核心操作。如果使用结构化数据模型存储图数据，需要将顶点和边分开存储，每行代表一个实体，通过耗时的连接（JOIN）操作实现图遍历［1］。考虑到图数据模型的灵活性和复杂性，现有的图数据库大多抛弃了传统的关系型模型，使用NoSQL［9］或原生图结构［10］进行存储。

由于图数据库使用了独特的存储结构，因此在业务流程中需要通过抽取、转换、加载（Extract，Transform，Load，ETL）过程摄取上游数据源。常见的应用场景为：用户的交易数据存储在事务型数据库中，如果有数据查询或报表的需要，则将数据导入数据仓库（简称数仓）进行分析；如果有图查询的需求，则需要再进行一次ETL 过程，将数仓中相关图结构导入图数据库进行查询。ETL 过程消耗大量计算资源，存在磁盘空间消耗大、数据延迟、运维繁琐等问题。

随着CPU 性能提升、DRAM 容量变大和 SSD 存储的流行，数据处理内存成为瓶颈［11］。近年来，随着向量化查询［12］、大规模并行处理［13］等技术的应用，新型数仓不仅在查询性能上具有优势，在扩展性、生态工具方面也逐渐成熟。对于图数据库来说，它专门为图的存储和计算设计，但在分布式扩展性能和查询性能上略有劣势。

如果使用新型数仓作为图数据库的后端并提供图查询的功能，那么一方面可以直接获得数仓的性能优势和成熟的生态工具，另一方面省去了繁杂耗时的ETL 过程，减少了存储压力，提高了数据新鲜度。本文提出一套基于数仓的图数据库系统PandaGraph。在存储方面，PandaGraph 结合数仓的列式存储特性，并考虑图查询过程和数仓查询执行特点，基于关系模型高效存储图数据。在查询方面，基于PandaGraph 设计了Gremlin-PandaNodeTree-Panda TableTree-SQL 的翻译过程，实现从图查询Gremlin 语言到数仓使用的SQL 语言的翻译转化过程。PandaGraph 使用多种优化方法对生成的 SQL 语句进行改写，提高图查询性能。

1 相关工作

1.1 标签属性图模型

目前的图数据库大多采用标签属性图模型［14］，简称属性图。属性图在简单图模型的基础上新增了标签来区分不同类型的顶点或边，顶点或边有零个或多个属性。属性图可定义为如下元组：

其中：V是顶点的有限集；E是边的有限集；λ为全函数，定义了顶点或边到标签的映射关系；σ为偏函数，定义了顶点或边到属性值的映射关系。

1.2 图存储模式

为了灵活存储图结构，现有的图数据库大多采用NoSQL 或原生 结构存 储图数 据。Titan［15］、HugeGraph［16］等图数据库使用键值对存储图数据，顶点作 为Key 键，Value 存储边 和属性。Neo4j［17］是一款基于原生图结构的图数据库系统，它通过链表将顶点、边和属性把前后指针串联起来，图遍历的过程即为链表遍历的过程。

现有的数仓大多采用列式结构化方式存储数据。在结构化模型中，数据以二维行、列进行存储，每行代表一个实体。IBM Db2［18］通过定义相关的图逻辑映射关系，与结构化数据库中的原始数据进行关联，并在上层统一组织元数据，生成SQL 进行图查询。SQLGraph［19］使用行存方式存储顶点和边，属性值信息采用JSON 列进行存储，标签信息单独存储在表格的一列中，数据用哈希算法打散存储。顶点表和边表单独存储ID 和属性，此外边表又拆分为主边表和从边表存储连接关系。这种存储方式不方便通过标签查找不同的实体，并且属性存储在JSON 中导致读取性能较差。SAP HANA［20］基于原有的列式数据库增加了图查询功能。在存储方面，它将顶点和边分别按标签值进行存储，属性存储在对应的表中，但它并没有针对图查询语句的特点进行存储优化，只是简单地将图数据拆分成结构化数据。

现有的基于结构化存储的图查询系统要么没有对底层存储结构修改，只完成了元数据映射关系，要么基于行式事务型数据库进行设计，简单地将图数据模式映射到存储引擎上，没有考虑到列式存储特点和图查询语句的特点。因此，如何在列式数仓上设计合理的存储结构是一个重要挑战。

1.3 图查询翻译

为了方便描述图中实体间的连接关系，业界提出了许多专有图查询语言，Gremlin［21］即为其中的一种。Gremlin 是一种灵活的图查询语言，它由基本的遍历步骤构成，通过将Gremlin 步骤串联起来，用户可在图上完成扩展遍历的过程。现有的许多图查询应用已经采用了大量的Gremlin 查询语句，使用数仓作为图查询引擎的后端需要将Gremlin 语言翻译转化为对应等价的SQL 语言，保证上层图应用的兼容性。

研究人员在图查询语言翻译SQL 方面进行了研究。SQLGraph［19］提供了一系列翻译的原语模板，将 Gremlin 步骤组装成SQL 语句，但生成的SQL 为多层嵌套，不方便调试和阅读，而且没有对生成的SQL进行深入优化。Cytosm［22］是将另一种流行的图查询语言Cypher 转换成SQL 的中间件，它依赖图拓扑在数据上构建模式，将Cypher 路径表达式切分成一系列rOCQ 结构，结合模板生成SQL。

将当前的图查询语言翻译成SQL 语句的工作大多比较简单，它们只是对某些步骤进行了模板式的替换翻译，因此生成的SQL 语句比较复杂，易读性较差。同时，由于Gremlin 语言灵活度较高，如何对翻译生成的SQL 语句进行等价改写也是一个值得研究的问题。

2 PandaGraph 系统

2.1 系统架构

结合数仓在数据分析上的优势，并实现图数据库的查询功能，本文设计了一套基于数仓的图数据库系统PandaGraph，从上到下分别为查询层、计算层和存储层，如图1 所示。

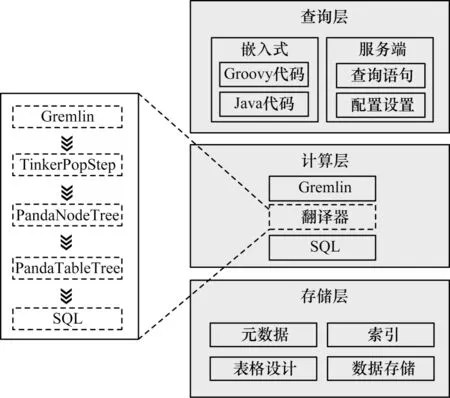
图1 PandaGraph 系统架构Fig.1 PandaGraph system architecture

在图1 中，查询层负责接收Gremlin 查询语句，是PandaGraph 的前端，可以通过API 代码或在网络上监听HTTP 请求获得查询语句。计算层将给定的Gremlin 查询翻译为对应的SQL 查询，首先通过TinkerPop 框架［23］获得对应的Gremlin 步骤，对于符合元数据的语句，依据不同的步骤特点构建关于遍历过程的PandaNodeTree。然后找到涉及的数据表，建立 PandaTableTree 并进行优化。最后将PandaTableTree 展开生成对应的SQL 语句，生成的查询SQL 将通过JDBC 发送到数据库，最终的执行结果将返回查询层。存储层对图数据建模，构建合适的元数据和表格设计。在构建表结构时，PandaGraph 在内存中维护了元数据，方便计算层进行元数据检查。

2.2 图结构与存储表映射

2.2.1 顶点表映射

为了存储顶点，PandaGraph 为每一种顶点单独构建顶点表，如图2 所示。顶点表定义了两类字段：第一类是保留字段ID，类型为BIGINT；第二类是用户定义的属性字段，相关属性数据类型可以从数据库的Schema 定义中获取。

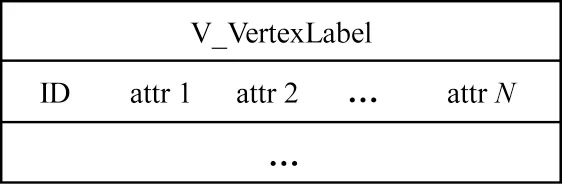
图2 顶点表存储 Fig.2 Vertex table storage

2.2.2 边表映射

与顶点类似，PandaGraph 为每一种边构建边表。边表保留字段有ID、FROM、TO，FROM 代表出点ID，TO 代表入点ID。3 种保留字段都采用BIGINT存储，属性字段从数据库的Schema 定义中获取，如图3 所示。图3（a）是以出方向为主的E_OUT 表，以FROM 和TO 作为主键列，图3（b）是以入方向为主的E_IN 表，以TO 和FROM 作为主键列，后续未加粗的字段为属性列。

图3 边表存储 Fig.3 Edge table storage

PandaGraph 在出方向为主的E_OUT 表中选取先FROM 后TO 作为键列，数据以先FROM 后TO 进行排序。如果需要找出边的信息，可以将FROM 键以约O（logan）的时间复杂度对ID 进行精确查找，迅速找到此时的出点（即TO 字段值）以及出边上的ID和属性值。由于同样为TO 字段进行了二次排序，在筛选出点时也可以使用粗略索引。图遍历的过程本质上就是顶点表和边表的JOIN 过程，通过将FROM和TO 作为主键列，可以快速找到出边遍历的下一步节点。类似地，如需找到入边的相关信息，只需在E_IN 上寻找即可。通过存储E_OUT 表和E_IN 表两份数据，在不同方向上遍历时可以灵活选择，提高JOIN 的性能。

3 PandaGraph 查询翻译和优化

3.1 查询翻译

3.1.1 Gremlin 基础

为兼容现有的大部分应用，PandaGraph 选择使用Gremlin 作为图查询的前端语言。本文对常见的Gremlin 基本步骤进行了总结和分类，如表1 所示，其中，起始、条件、扩展、映射选择、聚合和修饰分别用S、C、E、P、A 和M 表示。

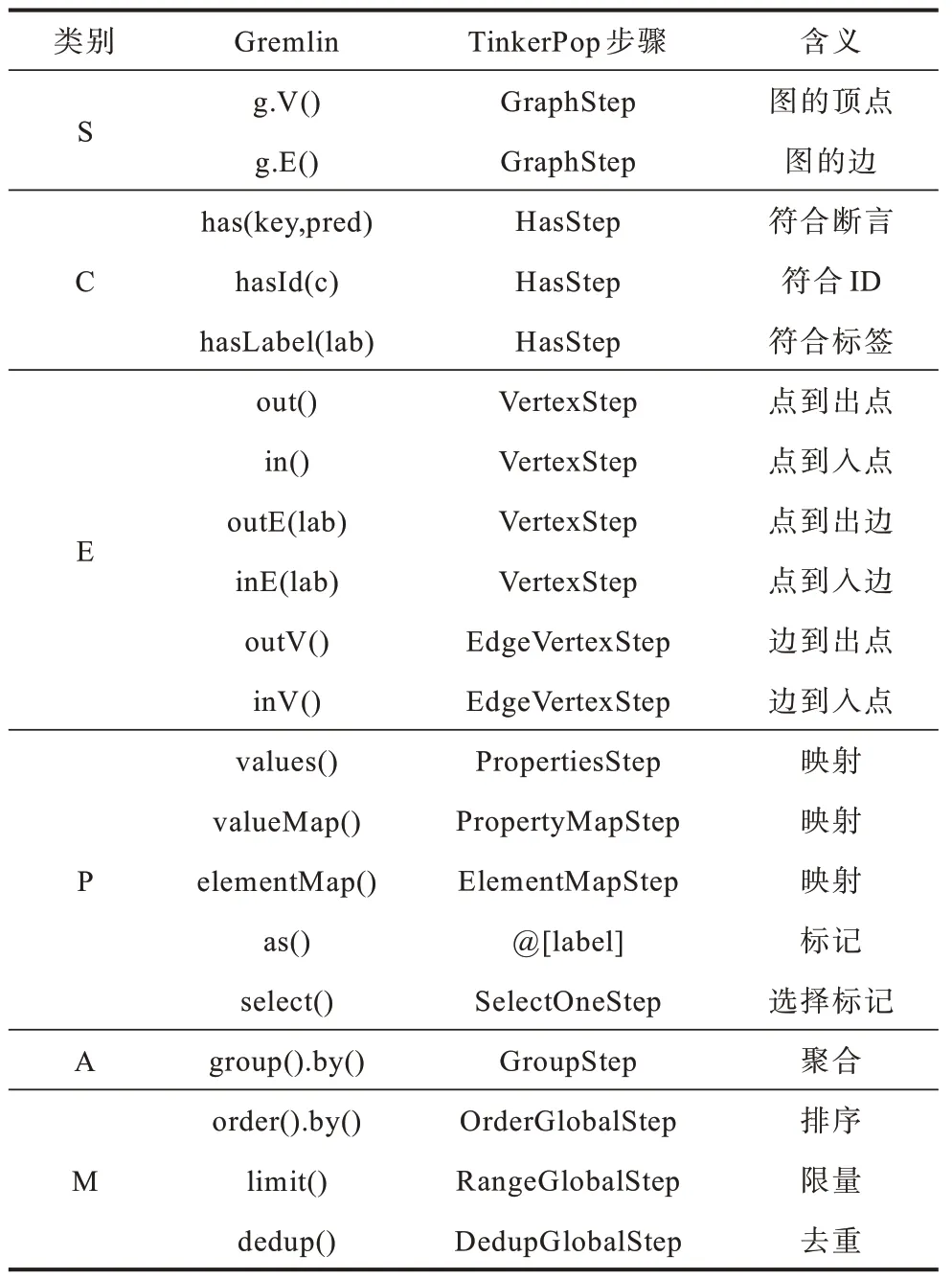
表1 Gremlin 常见步骤分类及含义 Table 1 Gremlin common step classification and meanings

依据步骤的作用，本文将常见的Gremlin 步骤分为起始、条件、扩展、映射选择、聚合和修饰6 类。后续将根据Gremlin 步骤的分类不同，根据基本步骤的特点进行Gremlin 到SQL 的翻译。以查询g.V（）.hasLabel（“Person”）.hasId（“1”）.out（“Create”）.has（“lang”，“java”）.order（）.by（“Id”，Order.ASC）.by（“name”，Order.DESC）.limit（2）.valueMap（“id”，“Name”）为例。起始的g.V（）步骤选择了所有顶点，hasLabel 和hasId 步骤选择了id 为1，标签为Person的顶点。后续的out 步骤和has 步骤遍历到java 编写的软件，通过order by 步骤将软件按id 和name 排序，并最终根据limit 和valueMap 步骤输出前两个的id属性和name 属性。

3.1.2 翻译概览

本文设计一套Gremlin-PandaNodeTree-Panda TableTree-SQL 的翻译过程，如图4 所示。左上部分为待翻译的Gremlin 查询（①）。PandaGraph 依据不同Gremlin 步骤的特性，将关于遍历的步骤构建成PandaNode 树，并把步骤的信息合并到树上节点中（②）。接着将PandaNodeTree 中涉及的数仓表找到，生成PandaTableTree（③）。最后通过PandaTableTree中的表信息和其他属性信息，找到SQL 的子句部分，翻译成SQL 语句（④）。

图4 PandaGraph 翻译过程Fig.4 PandaGraph translation process

3.1.3 PandaNodeTree 生成

PandaNodeTree 是图查询语句关于遍历过程的抽象树结构。PandaNode 中存储了当前遍历涉及的步骤、步骤的标签、遍历方向、过滤和聚合条件等信息。为了生成PandaNodeTree，需要对所有的Gremlin 步骤进行遍历判断，对于起始类（S）步骤，PandaGraph 创建根节点，对于扩展类（E）步骤，PandaGraph 构建关于扩展的PandaNode 并连接到树的叶子节点上，对于条件类（C）、映射选择类（P）、聚合类（A）和修饰类（M）步骤，PandaGraph 将对应的辅助信息存储在当前处理的节点中。

3.1.4 PandaTableTree 生成

PandaNodeTree 只对查询语句的遍历过程进行组合，而遍历涉及顶点表和边表之间的JOIN 操作，因此需要找出遍历涉及的存储表。PandaTable 在PandaNode 的基础上添加了当前遍历涉及的表格信息。具体生成方法见算法1。

算法1PandaTableTree 生成

PandaTableTree 生成算法首先找到所有起始的表。从元数据中找到所有的表，比对PandaNodeTree的根节点的标签断言，如果符合则添加到集合中。得到起始表后，起始表根据PandaNodeTree 进行扩展。如果当前PandaNode 代表的step 是VertexStep（包括顶点out、in 步骤和边outE、inE 步骤）时，这类Node 都是从当前顶点向外进行的遍历，那么需要通过元数据获取出入的边标签。如果步骤遍历的结果是边（outE 和inE 步骤），那么只需要将此边添加到对应的PandaTable 中。如果遍历结果是顶点（out 和in步骤），那么需要将顶点连接的边或顶点通过连接关系添加到PandaTableTree 中。如果当前PandaNode代表的step 是EdgeVertexStep（包 括outV 和inV 步骤），这类Node 从边指向顶点，那么将该边对应的顶点表添加到PandaTableTree 中即可。

3.1.5 SQL 翻译

获得关于查询存储表的PandaTableTree 后，可通过树信息生成最终的SQL。具体生成方法见算法2。

算法2SQL 生成

首先是SELECT 部分，为了避免SQL 中的重复表名问题，需要将表名重新进行映射。如果该表没有输出标记，则可以直接跳过；否则根据当前的信息输出对应的字段和普通表信息，包括聚合信息字段或DISTINCT 信息字段等和ID、对应属性值。

FROM 语句部分需要逐个输出相关的表名称，并将表别名信息通过AS 语句输出即可。

WHERE 语句包括两部分：一部分是原始的表上条件信息；另一部分是图遍历过程中的等价条件。前者只需要输出PandaTable 内的断言信息即可。后者需要将PandaTables 中前后两个表取出，根据连接关系（边的方向）等值连接ID 相关字段。

最后是GROUP BY、ORDER BY 和LIMIT 语句。这3 类的信息都存储在叶子节点中，因此只需要取出最后一个节点，判断是否有相关信息并输出即可。

3.2 基于规则的优化

3.2.1 表选择

图遍历的过程实际就是顶点和边表进行ID 等值连接的过程。数仓无法创建基于数字的精准索引，因此为了加速连接过程，PandaGraph 依靠主键的排序索引存储了两张边表，方便不同方向的遍历查询。

本文记遍历扩展步骤为ε，扩展的表名和方向用下标表示，如εEab←Va表示从顶点a向外扩展到边ab。对于out 的遍历，需要通过FROM 字段寻找TO 字段，其中FROM 字段是索引的核心，因此可以使用FROM 在前、TO 在后的EO 表（E_OUT）：

in 遍历情况类似，需要通过TO 字段寻找FROM字段，其中TO 字段是索引的核心，使用TO 在前、FROM 在后的EI 表（E_IN）：

在算法2 的翻译过程中，只需要在添加边表时考虑方向即可。对于out 方向使用E_OUT 表，对于in 方向使 用E_IN 表。

3.2.2 JOIN 选择

等值连接（EQUI JOIN）将不同的表依据条件等值拼接，符合图上遍历的定义。但对于g.V（）.out（）.dedup（）.count（）等类似的查询，如果满足：1）只在最终步骤的输出结果；2）中间重复结果需要去除，则可以使用半连接（SEMI JOIN）进行替代。等值连接根据匹配的数量重复返回多次，而半连接仅返回某个表的元组且最多返回一次，可以传输更少的元组，带来更高的查询效率。out 遍历可以优化如下：

in 遍历的优化类似，同时这个过程是连续的，如果中间同样不需要输出结果，则最后一步的SEMI JOIN 可以在前面步骤中提前进行。

3.2.3 遍历去除

上述的遍历翻译过程需要中间边做支点，顶点到顶点的遍历涉及两张顶点表和一张边表：

1）起点去除。如果在遍历的起点只需要ID 信息，那么可以省略对第一张顶点表的JOIN 操作，只需要对中间边表和最终的顶点表进行JOIN 操作。因为中间边表的FROM 或TO 字段已经存储了顶点的ID 信息，此时的遍历操作可简化如下：

2）结尾去除。如果在遍历的结尾步骤只需要ID信息，或借助ID 信息即可进行处理（如count 步骤，只需要计数ID 信息），则此时只需要对开始的顶点表和中间的边表进行JOIN 操作，最终步骤的ID 信息存储在边表的FROM 或TO 字段中：

3）中转去除。在进行遍历的过程中，经常出现多步遍历操作，原始的生成方法可以生成中间以顶点作为支点进行JOIN 的遍历过程。如果在此过程中不需要对中间的顶点表进行条件筛选或输出，则可以将中间的顶点省去，用边表中的FROM 或TO 字段中的ID 作为遍历中间支点：

遍历去除过程可见算法3。

算法3遍历去除

中转去除的过程需要考虑当前节点、父节点和祖父节点，对“边-顶点-边”的序列进行判断和去除。起点和结尾去除的过程只需要考虑根和叶子节点即可。遍历去除减少了JOIN 的数量，提高了查询效率。

3.2.4 DISTINCT 下推

在遍历的过程中有时需要对最终结果进行去重，如果只在最后一步去重，中间遍历结果的重复数据增加了数据传输的开销，也增加了JOIN 的表构建和探测的时间。因此，当遍历的某一步需要进行去重操作时，可以将该步的去重操作下推到之前的所有遍历步骤中：

DISTINCT 下推的过程见算法4。从叶子节点出发向上遍历，将所有可以DISTINCT 下推的节点进行标记即可。

算法4DISTINCT 下推

3.3 翻译优化完备性和正确性讨论

Gremlin 语言的灵活度大，图遍历的表达方式多样，其基本步骤可分为变换（Transform）、过滤（Filter）、副作用（Side Effect）和条件（Branch）4 类［19］。本文的翻译涉及变换、过滤和副作用3 类共28 个步骤，已经可以满足常见的遍历场景。

本文支持的步骤中条件、映射和选择、聚合、修饰这4 个步骤与SQL 语言一一对应，可以直接进行翻译。起始步骤主要涉及的顶点表和边表，可以通过元数据和断言获取。扩展步骤表示图遍历的移动过程，与JOIN 操作等价，因此可以通过“顶点-边-顶点”的连接进行翻译。同时，上述优化方法不改变实际的遍历含义和执行结果，是等价的查询语句替换。综上，本文提出的翻译和优化方法可以保证翻译和优化的正确性，后续实验章节也对典型的例子进行了交叉验证。

4 实验与结果分析

4.1 实验设置与实验数据

本文实验在配置为32 核Intel Xeon E5 处理器、128 GB内存、12 TB HDD 磁盘和CentOS 7.9 的单机上进行。PandaGraph（PG）使用Java 编写，底层数仓为Doris 1.1。根据实现方式不同，对比图数据库为：使用键 值对存储的 HugeGraph 0.12（HG）和NebulaGraph 3.0（NG），链表存储的Neo4j 4.1（N4），原生图存储的TigerGraph 3.6（TG），关系型存储的SQLGraph（SG）。底层采用PostgreSQL 14.5 实现。

本文运用Graph500（G）、Flickr（F）、LiveJournal（J）、Twitter（T）、LDBC1（L1）、LDBC10（L10）数据集进行实验，如表2 所示。

表2 实验数据集 Table 2 Experiment datasets

4.2 数据导入和存储

数据导入时间对比如图5 所示。除了Twitter 数据集上TG 最快外，其他情况下PG 的导入速度最快，PG 较TG、N4、HG、SG 和NG 有最多1.71、2.50、5.62、14.42 和18.19 倍的导入性能提升。HG 未能成功导入LDBC10 数据集。

图5 数据导入时间对比Fig.5 Comparison of data import time

以L1 数据集为例对导入时间进行分解，如图6所示。由于数据模拟的真实稀疏图边数量多，因此导入时间也较长，占TG、HG、N4、SG 和PG 总导入时间的23.6%～71.8%。NG 在多线程导入时不区分顶点和边，在图中统一表示，这部分占比81.4%。对于PG来说，其他时间主要为数据建表操作，而LDBC 数据集表数量较多，有59 张表，开销约占总时间的9.3%。其余图数据库的其他时间占总时间的12.6% 到65.4%，这部分时间主要用来进行数据预处理、建立索引和内存管理等操作。

图6 数据导入时间分解Fig.6 Data import time breakdown

不同图数据库的存储空间占用结果如表3 所示。HG 和NG 的底层键值对系统采用LSM-Tree 结构［24］存储，存在写放大问题［25］，因此空间占用较多。SG 存储了多份数据和索引，加上行式存储的压缩效率不高，因此空间占用最大。N4 将节点和边用链表的方式存储起来，需要额外存储链接信息。TG 没有公开存储设计细节，其存储空间占用仅次于SG。PG底层数仓采用列式存储，并且采用了数据压缩技术，即使存储了两份边表，存储空间占用依旧是最少的。

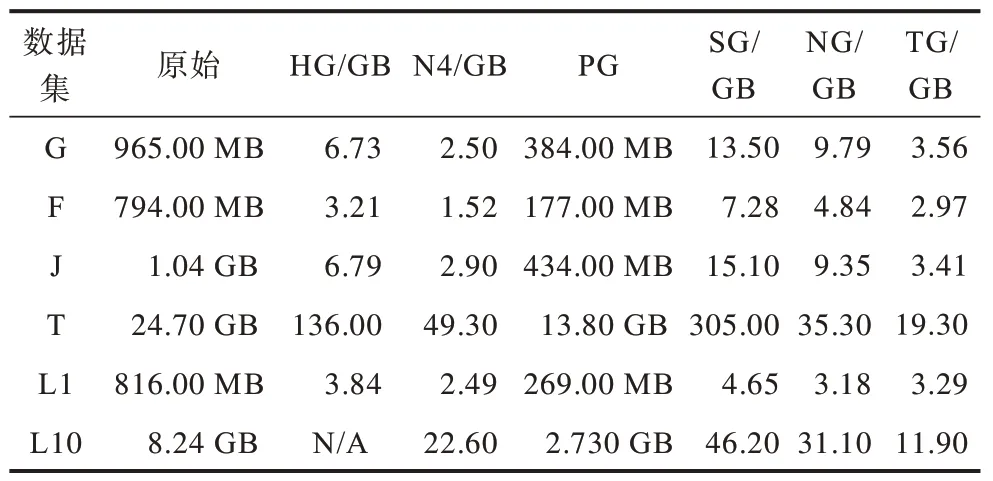
表3 存储空间占用对比 Table 3 Comparison of storage space occupancy

4.3 翻译正确性验证

为了验证PG 翻译Gremlin 的正确性，本文在L1数据集上对不同类型的查询语句进行验证，结果如表4所示。正确性验证分为6类，包括起始（S）、条件（C）、映射选择（P）、扩展（E）、聚合（A）和修饰（M），与前文介绍的Gremlin 步骤分类对应。每类查询包含3 个语句，共计18 个。本文同时书写了相同语义的Cypher 语句供N4 执行，与HG 和N4 的结果交叉验证。3 种图数据库的查询结果相同，表明PG 的翻译结果是正确的。

4.4 k 跳算法查询时间

为了探究PG 的性能信息，本文选取了k跳（k-hop）算法进行测试。k跳算法是经典图查询算法之一，从起点出发找出k层上与之关联的节点数量。例如，当k=2 时，对应的Gremlin 查询语句写为g.V（ID）.out（）.out（）.dedup（）.count（）。

本节对 低k跳（k=1，2，3）和 高k跳（k=4，5，6）两种类型进行了研究。使用前文所述所有优化方法对PG 生成的SQL 查询进行优化，超时时间设置为300 s。与其他数据库不同，TG 首先通过安装（install）步骤预翻译并优化查询，然后通过运行（run）步骤查询安装后的语句。对于确定模式的查询来说这种优化是有效的，一次安装后可多次运行查询，但对于临时查询来说，安装过程显著增加了查询时间。如果仅考虑安装后的查询时间，TG 在大多数情况下都表现最优。此外，由于TG 不开源也不支持查看查询计划，本文无法详细分析安装和运行期间执行的操作，因此后文仅列出了TG 的实验数据，不对查询的结果进行分析和对比。

在低k跳实验中，本文随机选取了100 个有k度邻居的点，记录下几何平均查询时间，如表5 所示，其中叹号加粗的数据表示超时的查询个数。

当k=1 时，即查询当前点的邻居数量时，不同图数据库的平均查询时间比较稳定。PG、HG、NG、SG通过主键索引，N4 通过B 树索引直接定位到对应的节点。Twitter（T）数据集较大，N4 和NG 仍保持了相对稳定的性能，其余图数据库性能都稍有降低。总地来看，N4、SG、NG 和PG 的查询性能都优于HG。

当k=2 时，PG 和SG 将顶点和边存储在不同的表中，需要进行表JOIN 操作，但 PG 进行了数据的拆分和聚合，当数据量小时性能较差，SG 在G 和T 数据集上生成的嵌套SQL 使优化器错误地选择了SORT MERGE JOIN，查询性能最差。对于HG、NG 和N4来说，前两者通过键值对将顶点和边存储在一起，后者用链表的形式将顶点和边链接起来，在存储空间上具有连续性，因此性能最好。

当k=3时，G 数据集的结果较大（平均31 000 ms），N4、HG 和NG 都需要顺序遍历所有的结果，而PG 生成的多线程计划可以分割JOIN 任务来并行处理，因此PG 更有优 势，相 比N4 和NG 有1.27 和5.88 倍的性能提升。由于SG 需要JOIN 多张主从顶点表和边表，因此耗时最长。F 和J 数据集的结果并不大（平均692 ms、2.0×104ms），很难抵消PG 执行JOIN 的开销，因此性能表现最差。数据量最大的T 数据集上（平均结果2.2×107ms）也有类似的表现，除PG 外其余图数据库都出现了超时的情况。

在高k跳实验中，本文随机选取了50 个有k度邻居的点，几何平均查询时间如表6 所示，其中叹号加粗的数据表示超时的查询个数。

表6 高k 跳（k=4，5，6）查询时间 Table 6 High k-hop（k=4，5，6）query time 单位：ms

当k=4 时，由于遍历的最终结果较大，HG 和SG在G、F 和T 数据集上都有超时。N4 的查询计划显示需要进行先遍历后去重最后聚合的操作，在这个过程中步数较多，较大的中间结果增加了遍历的开销，而且此时N4 无法准确预估每步的中间结果数量（提示为0），因此也无法给优化器提供更多的信息来做进一步优化。PG 相比N4 有4.23、1.07 和3.07 倍的性能提升。

当k=5 时，遍历的结果继续增大，如果没有中间去重的优化，中间结果的计算的压力进一步增大。NG 的查询计划同样显示没有对每步的中间结果进行去重操作，因此出现了多次超出内存限制或RPC错误。类似地，HG 在全部的数据集上都出现了超时，N4 只在J 数据集上完成了测试，在T 数据集上出现了超出内存的错误。PG 相较N4 有18.5 倍的性能提升。

当k=6 时，只有PG 全部在合理时间内完成所有的查询任务，此时生成的查询计划可以将大量的中间数据进行划分和去重，通过多线程同步进行，同时多步聚合操作进一步提高了聚合的效率，因此可以在合理的时间内完成查询任务。

4.5 规则优化

根据PandaGraph 的翻译过程，k跳算法是“顶点-边-顶点”的JOIN 遍历过程。通过前文的各种优化规则可生成更优的SQL 语句。本节把朴素翻译生成的SQL 记为O0，SEMI JOIN 优化记为O1，去除起点JOIN 记为O2，去除结束点JOIN 记为O3，去除中间顶点JOIN 记为O4，DISTINCT 下推记为O5。

在4 种数据集上随机选取了50 个有6 度邻居的起始点来研究不同优化规则对查询的性能影响，查询的几何平均时间如表7 所示，其中，超时用加粗叹号进行标注，O2～O5 的执行时间下方标注了相比前者优化的加速比。通过使用不同的优化方法，相比O1 优化最好可以得到1.37 倍的性能提升。

表7 SQL 规则优化下的查询时间 Table 7 Query time of SQL rule optimization 单位：ms

在所有的数据集上，原始O0 查询都无法在规定时间内完成测试。这是因为不使用DISTINCT 的JOIN 的结果约为dˉk（其中dˉ是图的平均度数），在k较大时结果十分庞大，需要较长的时间进行数据处理。O1 优化就是一个去重过程，通过将INNER JOIN 转化成SEMI JOIN，在JOIN 过程中只传输了去重的顶点，减少了中间结果传输，带来了显著效果。理论上O2～O5 操作都减少了JOIN 的步骤，降低了计算量和传输量，应该带来性能的提升，但不同的优化方法在某些数据集上都出现了不同程度的性能下降，甚至O4 优化在T 数据集上出现了42 次超时。以T 数据集上的O4 优化为例，通过查看生成的查询计划，PG错误生成了Shuffle Join 计划，带来了大量的数据传输开销。如果优化器正常，可在其他数据集上获得1.11、1.07、1.23 和1.04 倍的性能提升。综合来看，最优可获得1.22、1.37、1.30 和1.13 倍的性能提升。这说明对不同的数据集，数仓的优化器也起重要的作用，如果不能提供合适的统计信息并生成正确的执行计划，将会严重影响查询性能。

4.6 表选择优化

为了探究遍历过程中表选择与查询时间的关系，本节修改了上述k跳算法的遍历方向，探究k=1或k=6 时选择不同的表对性能的影响，将默认不优化的查询记为O0，将修改了其中i个E_OUT 表为E_IN 表的查询记为Oi。本文在4 种数据集上随机选取了50 个有1 度或6 度邻居的点，几何平均查询时间汇总如表8 和表9 所示，其中，括号内数字为相比前者优化的加速比。

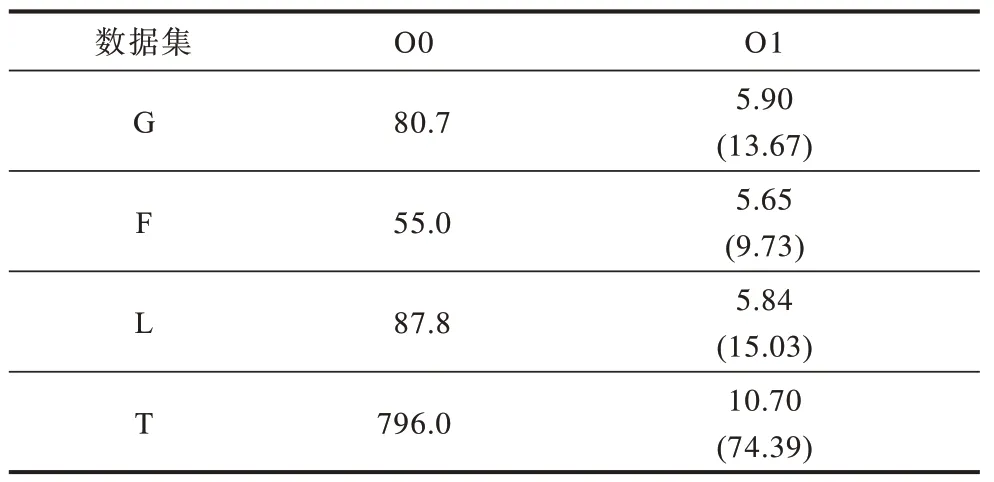
表8 k=1 时表选择优化的查询时间 Table 8 Query time of table selection optimization when k=1 单位：ms

表9 k=6 时表选择优化查询时间 Table 9 Query time of table selection optimization when k=6 单位：ms

当k=1 时，索引的性能对查询时间有较大影响。当不使用表优化时，PG 的主键建立在FROM 键上，但需要对TO 键进行查询，因此需要扫描全部的数据，随着数据量的增加，查询时间也随之增加。如果使用主键为TO 的E_IN 表，则可以直接定位对应的数据，减少了不必要的磁盘读取。表选择优化在4 种数据集上有最少9.73 倍和最多74.39 倍的性能提升。由于访问模式相同，使用E_IN 表时查询的时间和反方向的k=1 跳查询时间相差不大。

当k=6 时，同样可以带来性能提升，这是因为多表JOIN 同样需要对中间结果进行等值匹配，选择合适的主键可以减少不必要的数据读取，在4 种数据集上总计可获得1.19 倍到1.43 倍的性能提升。

4.7 表结构优化

为了研究表主键选择对查询时间的影响，选取了以ID 为主键作为基准，与PandaGraph 系统以FROM/TO 为主键进行对比。本节选取1～6 跳的查询语句，在4 种数据集上选取了100 个有k度邻居的点，查询时间的几何平均值见表10。

在低k跳时，PG 使用顶点作为主键可以获得最多265 倍的性能提升，在高k跳时，PG 也能获得最多2.7 倍的性能提升。这是因为在遍历的过程中需要对中转ID 进行定位，使用FROM/TO 为主键时可以通过主键索引命中对应ID。在低k跳时，时间取决于ID 的定位时间，因此修改表主键后加速比较大，在高k跳时，主要依靠动态布隆过滤器进行过滤，修改主键可加速查询，但性能提升不如低k跳时明显。

5 结束语

本文设计并实现一套基于数仓的图数据库系统PandaGraph。PandaGraph 结合数仓的列式存储特性，在兼顾高效图查询的同时，降低导入时间，减少空间占用，并提出一种Gremlin 语言翻译SQL 的方法，在保持原有图查询应用兼容性的前提下高效完成图查询。实验结果表明，PandaGraph 在经典的k跳算法中相较现有专有图数据库可获得18.5 倍的查询性能提升。下一步拟提出更加完备的Gremlin代数规则，实现复杂语句的翻译和优化，同时对数仓的底层数据结构进行优化，提高低k跳的查询效率。