基于分布式扰动的文本对抗训练方法
沈志东,岳恒宪
(武汉大学 国家网络安全学院,武汉 430000)
0 概述
对抗样本是通过向输入的样本添加一个细微的扰动来增加机器学习模型产生的损失[1-2],导致模型以高置信度给出一个错误的输出。目前的机器学习模型,即使是最先进的卷积神经网络都无法正确分类对抗样本。对抗训练(Adversarial Training,AT)是训练模型可以正确分类未修改的原始样本和对抗样本的过程,不仅能够提高神经网络的鲁棒性,而且还能够增强模型的泛化性能。
与图像分类领域取得的成功不同,AT 不能直接应用于自然语言处理(Natural Language Processing,NLP)分类中的任务,这主要是因为其无法为NLP 中的任务计算扰动输入,输入由离散符号组成,而不是在图像处理中使用的连续空间。文献[3]提出一种新的策略来改进NLP 任务的对抗训练,即将对抗训练应用于连续的词嵌入空间,而不是文本的离散输入空间。该方法的优点是保留了图像处理领域的背景,并且具有正则化的效果,显著提高了任务性能,并在多个文本分类任务中实现了最优的性能,它的另一个显著优势是架构简洁,因为只需要通过损失函数的梯度来获得对抗扰动。梯度计算是在模型训练期间更新模型参数的标准计算过程,可以以较小的计算成本在词嵌入空间中获得对抗扰动,而无须添加任何额外的复杂架构。
以往的研究主要是将对抗训练应用于图像分类任务中。对抗性扰动通常涉及对许多真实值输入的较小修改,对于文本分类,输入是离散的,通常表示为一维独热向量。由于一维独热向量集不允许无限小的扰动,因此将扰动添加在连续的词嵌入而不是离散的词输入。传统的对抗训练可以解释为正则化策略[1-2],也可以解释为对能够提供恶意输入的对手的防御。
特定的攻击算法不会生成所有可能的对抗样本,解决内部最大化问题是AT 成功的关键。文献[4-5]方法训练多种攻击手段,可以看作是对文献[6]内部问题的更详细描述,但仍然缺乏对许多不同攻击方法的准确描述。由于文本不能像图像一样直接进行处理,主要是因为文本不是连续变量的,只有将文本通过嵌入层后才能如AT[7]那样连续解决文本对抗分布训练(Textual Adversarial Distribution Training,TADT)的最小化问题。
本文提出一种基于概率分布式训练的文本对抗训练方法,旨在提高神经网络的鲁棒性和泛化能力。通过将每个输入示例的对抗分布最大化,并最小化对抗分布的预期损失,使用可训练参数的对抗分布,引入熵的正则化项来防止对抗分布坍缩为一个点,并通过生成模型直接生成对抗分布的参数,降低训练成本,改善深度学习模型在面对不同攻击时的防御性能。
1 相关研究
对抗样本最初是由SZEGEDY 等[1]在2013 年提出并定义的。对抗样本是在输入数据上人为加入人类视觉无法察觉的非随机扰动,以改变目标模型的推理结果。文献[8]基于盲点假设提出一种Limitedmemory BFGS(L-BFGS)算法来生成对抗样本。文献[2]基于线性假设利用损失函数在原始图像像素值上的梯度来降低损失函数值,并通过优化提出一种计算成本大幅降低的快速梯度符号法(Fast Gradient Sign Method,FGSM)。之后基于FGSM 方法衍生出许多算法:如迭代梯度符号法(I-FGSM)[9]、动量迭代快速梯度符号法(MI-FGSM)[10]等。另外,一些基于梯度掩蔽来防御白盒攻击的算法被提出,最具代表性的如防御性蒸馏方法[11]。此后,对抗样本的攻防不断迭代。基于优化的C&W 攻击[12]打破了实现梯度掩蔽的防御蒸馏,解决了FGSM[13]中的一些基本缺陷。文献[14]利用对抗样本与正常样本的数据差异进行检测,重新设计网络结构或增加网络子模块,消除了对抗干扰,将对抗样本恢复为正常数据[15]。
在对抗样本的攻防发展中,由于研究人员制定的指标和标准不统一,衡量各自算法的优劣成为制约对抗样本研究发展的重要因素。为此,研究人员将他们的算法应用到各种竞赛中,如NIPS 对抗样本攻防[16]、GeekPwn 的CAAD 对抗样本攻防、IJCAI 对抗样本竞赛等。大量的攻防算法在这些比赛中得到了充分的验证,很多算法也成为了后续研究的基础,极大地促进了对抗样本的发展,比如著名的ATN 全卷积对抗样本生成网络就是通过生成对抗网络不断训练得到的。对抗样本生成器可以批量生成对抗样本,大幅压缩了以往攻击所需的计算时间,成为基于生成器的对抗样本攻击算法中极具启发性的算法。
近年来,基于深度学习技术本身可能存在的内在缺陷,研究人员进行了更加深入的分析和研究。由于深度模型具有黑盒特性,因此提高模型的可解释性可以解决基于对抗样本的AI 安全问题[10,17]。由于对抗样本是可迁移的,因此了解特征的生成方式至关重要[18-20],研究人员已经从理论上证明了模型的鲁棒性或安全边界。然而,对抗样本的根本原因当前尚无定论和发展,例如QIN 等[21]否定了之前局部线性导致对抗样本的观点,证明了局部线性的特性可以提高鲁棒性。一般来说,大多数人认为鲁棒性和准确性之间存在平衡,引入对抗性训练会降低原始数据的准确性。然而,XIE 等[22]的研究结果表明,对抗训练可以同时提高模型的准确性和鲁棒性,他们观察到之前结合干净样本和对抗样本的方法都没有提前进行区分,因此提出一种新的训练方案,即用两个简单但是高效的批归一化层分离两个文本对抗分布,能够通过对抗样本改进模型。但是,提高模型的鲁棒性和对不同攻击的泛化性,仍需进一步探索。
2 问题的形式化描述
2.1 一般问题的描述
本文主要考虑的是标准分类任务,其基础数据集D分布在成对的示例xi∊Rd和相应的标签yi∊[k]上。AT 可以表述为极小极大问题,即:
其中:fθ表示参数为θ的神经网络模型,其输出是所有类的概率;S={δ:‖δ‖∞≤ϵ}是一个扰动集,ϵ>0;L为损失函数;n为类别数。本文方法还可以扩展到其他威胁模型,如L2 范数。
极小极大问题通常是顺序求解的,即首先通过求解内部最大化来生成对抗样本,然后根据生成的对抗样本优化模型参数。本文考虑一个基于单词替换的简单模型,其中输入句子中的每个单词都可以被其同义词替换。给定一个句子和一组同义词,确保使用对抗训练的模型预测不会被基于单词替换的任何扰动所改变。然而,由于可能扰动的数量随句子长度呈指数增长,因此数据扩充无法覆盖输入句子的所有扰动。
2.2 文本问题的描述
如前文所述,对抗训练虽然有效,但并非没有问题。针对特定攻击的对抗训练可能会导致模型过度拟合某种攻击方式[9,23-25],影响训练模型抵抗其他攻击的能力,这主要是因为单一的攻击算法无法探索对抗空间中所有可能的扰动,降低了模型的泛化性[23,26]。为了解决这些问题,本文通过文本对抗分布训练来计算每个输入对抗性扰动的分布,而不是仅找到局部最优解。本文从p(δi)中采样的对抗分布被添加到每个自然示例xi中形成对抗样本,其中p(δi)包含在S中。假设给定一个合适的损失函数L(θ,x,y),例如神经网络的交叉熵损失函数,通常θ∊RP是模型参数集。本文的目标是找到能使期望E(x,y)~D[L(θ,x,y)]最小化的模型参数θ:
其中:P={p:supp(p)⊆S}是一组支撑包含在S中的分布。式(2)的内部最大化目标是学习一个对抗分布,该分布中的任何一点都是这个样本的对抗样本。相反,外部最小化的目标是通过最小化由内部问题引起的最坏情况对抗分布的预期损失来训练模型的鲁棒性。值得注意的是,AT 是TADT 的特例,是指分布族P只包含delta 分布时的特例。
对于TADT 的内部最大化,即:
从式(3)可以看出,通过解决TADT 的内部问题获得的最优分布有可能退化为delta 分布,这将导致对抗分布无法覆盖更多的对抗样本,TADT 变为了AT。为了解决这个问题,在目标中添加了一个熵的正则化项,即:
其中:H(p(δi)) 是p(δi)的熵;λ是平衡 超参数;L(p(δi),θ)表示整体损失函数。为了防止整个分布退化为一个点,通过加入熵λH(p(δi))来防止这种情况发生。
3 TADT 的通用解决方法
在图像对抗攻击中,只需改变图片中的一个或几个像素点就可达到攻击者的目的。在文本攻击中,可以通过仅改变词嵌入向量中的某些元素来实现攻击者的目标。因此,在对抗训练中,希望能够训练分类器,使其对嵌入的扰动具有鲁棒性。
由于在预训练的词向量空间中同义词的词向量之间的距离很近,可以认为每个样本都有一个对抗分布空间,这个空间中的每个点都是它的对抗样本。将T个单词的序列表示为{w(t)|t=1,2,…,T},并将相应的目标表示为y。为了将离散词输入转换为连续向量,将词嵌入矩阵定义为V∊R(K+1)×D,其中,K是词汇表中的词数,每行vk对应于第i个词的词嵌入。
仅通过一种攻击方式来增加对抗扰动是有缺陷的,由于它只能防御这一种攻击方式。因此,需要为每个样本添加一个对抗扰动分布。本文的目标就是找到每个样本的对抗分布。
3.1 显式密度对抗分布
对输入数据周围的对抗空间建模的方法是具有显式密度函数的对抗分布TADTEXP。为了定义pΦi(δi)在S上的适当分布,本文采用随机变量的变换,如式(5)所示:
其中:Ui是从均值为μi和标准差为σi∊Rd的正态分布中采样得到的,Ui在通过tanh 函数转换后乘以ϵ得到δi。本文定义的显式对抗分布首先假设每个维度的均值和标准差满足|μi,j| 为了解决内部问题,需要估计参数ϕi上预期损失的梯度。一种常见的方法是低方差重参数化技术[5,12],如图1 所示,用相应的可微分变换代替目标变量的采样过程。运用该技术,梯度可以直接从样本反向传播到分布参数。在本文方法中,通过δi=ϵ·tanh (ui)=ϵ·tanh (μi+σir)重新参数化ϕi,其中,r是遵循标准高斯分布N(0,1)的辅助噪声向量。增加的熵的正则化项变为: 式(7)是对数密度(即熵)的估计。在实际中,可以通过蒙特卡罗采样逼近式(6)中的期望,并继续对ϕi执行T步梯度上升来解决内部问题。在获得最优参数后,再使用对抗分布更新模型参数θ。 TADT 方法的核心是内部最大化问题的求解,形式化表示见式(6)。本文的基本思想是用可训练参数Φi重参数化内部问题的分布。运用参数化pΦi(δi),内部问题转化为最大化预期损失Φi。 与图像领域不同,组成文本的词语一般都是以 独热向量或者是词索引向量来表示的,可以视作是离散的,而非图像中连续的RGB 值,如果直接在原始文本上进行扰动,则有可能扰动的方向和大小都没有任何明确的语义对应,但词嵌入表示可以是连续的,因此需要对文本进行一些处理。如上所述,本文将对抗性扰动直接应用于词嵌入,而不再是应用于原始输入。为了定义词嵌入的对抗性扰动,表示一个串联[vˉ1,vˉ2,…,vˉT]的词嵌入向量序列(归一化)为s、y,其中模型条件概率p(y|s;θ)给定s,θ是模型参数,那么s上的对抗扰动rTADT定义为: 为了使式(8)中定义的对抗性扰动具有鲁棒性,本文将对抗损失定义为: 其中:N是标记示例的数量。在本文的实验中,对抗训练是指使用随机梯度下降[29]负对数似然加上LTADT。这里需要计算最小化损失函数的扰动分布,选择负对数是为了改变梯度方向,选择朝着梯度上升的方向添加扰动,将这样的扰动分布输入模型进行训练,再进行反向传播更新模型参数,从而达到提升模型鲁棒性的目的。 AT 和TADT 之间的主要区别在于:对于每个自然输入xi,AT 找到一个最坏情况的对抗样本,TADT学习包含各种对抗样本的最坏情况的对抗分布。由于可以通过多种攻击生成对抗样本,本文预计这些对抗样本可能位于对抗分布的高概率区域,因此最小化该分布的预期损失会导致训练好的分类器具有更好的泛化能力,并可以使模型抵抗交叉攻击。此外,在式(4)中添加了一个熵的正则化项,以防止对抗性分布退化为单一的对抗性训练,与概率加权词显著性(Probability Weighted Word Saliency,PWWS)等单一攻击方法相比,发现了更多的对抗样本。文本对抗分布训练也考虑了同义词嵌入向量的相似性,具有更好的泛化能力。最大限度地减少这些不同对抗样本的损失,有助于在输入的自然样本周围学习更平滑、更平坦的损失曲面。因此,TADT 比AT更能提高整体鲁棒性。 算法1TADT 的通用算法 输入训练数据D,损失函数L(p(δi),θ),每次梯度估计的蒙特卡罗采样次数k,训练批次N,学习率η 输出准确率 1.将文本的独热向量转化为词嵌入向量W,初始化模型参数θ 2.初始化rTADT 3.用式(9)计算k 次蒙特卡罗损失 4.更新rTADT 5.使用随机梯度下降法更新模型参数θ 第3.3 节提到的算法为TADT 提供了一种学习显式概率分布的简单方法,但它需要计算每个输入样本的分布参数,进行多次迭代,时间开销太大。与之前基于对抗性攻击的AT 相比,TADTEXP大约慢k倍,因为ϕi梯度的每一步都需要k次蒙特卡罗采样。本节提出一种效率更高的训练方法,能够直接生成TADTEXP参数(μi,σi)的内部分布,并将此方法命名为TADTEXP-GE。 本文没有继续选择去学习每个数据xi可能存在的概率分布,而是选择去学习映射gϕ:Rd→P,它定义了对抗分布pϕ(δi|xi)以条件概率的方式作为每个输入。本文通过映射生成器网络实例化gϕ,以样本xi作为输入,输出参数为(μi,σi)。这种方法的特点是生成器网络可以直接学习给定样本的扰动空间概率分布的参数,而不需要进行多次采样[3,30],即不再需要对每个数据xi进行过度优化,可节省大量时间。 在TADTEXP-GE对抗训练中,由于分布未知,假设每个样本服从正态分布,并将TADT 的极小极大问题重写为: 本节用VAE[31]来实现生成器网络,通过它可以直接计算得到每个输入样本对抗分布的参数。此外,该目标还是数据真实对数似然的有效下界。 本节在文本分类的数据集上进行实验,使用CNN 和LSTM 两个神经网络模型来评估本文提出的TADT方法和其他防御方法的性能,如图2所示,图2(a)是基于CNN 网络架构,图2(b)是基于LSTM 网络架构。实验通过多种攻击方法进行测试。 图2 神经网络模型整体架构Fig.2 Overall architecture of neural network model 文献[32]描述一种概率加权词显著性(PWWS)的贪心算法,并在同义词替换策略的基础上,提出一种由词性显著性和分类概率确定的词替换方法,将PWWS 算法作为对样本进行词级扰动的手段,使用GA 对扰动后的样本进行优化。文献[33]提出一种基于梯度下降的攻击方法UAT,并给出基于令牌的梯度引导搜索方法。本节对每个数据集随机选择的1 000 个测试样本采用PWWS、GA 和UAT 3 种攻击算法测试它们对对抗攻击的防御性能,并与对抗训练(ADV)[34]、基于间隔传播(IBP)等防御方法[35]进行比较。 本节首先在互联网电影数据库(IMDB)[23]文本分类数据集上进行训练,分别使用LSTM 和CNN两个模型完成文本分类任务。LSTM 首先通过词嵌入网络将每个输入词转化为近似连续可微分的向量,然后根据具有D维隐藏状态的双向递归神经网络,在训练过程中计算出每个词的对抗分布,在得到每个词的对抗分布模型后训练网络参数。CNN 与LSTM 模型流程类似,通过预训练的GloVe[36]词嵌入模型得到单词的词向量。TADT 模型使用对抗分布损失进行训练,且它们的超参数在验证集上进行调整。表1 和表2 所示为CLN 干净数据集与PWWS、GA 和UAT 3 种攻击算法在CNN 和LSTM 模型上的准确率。 表1 不同方法在CNN 模型上的准确率 Table 1 Accuracy of different methods on CNN model % 表2 不同方法在LSTM 模型上的准确率 Table 2 Accuracy of different methods on LSTM model % 从表1 和表2 可以看出,TADT 在干净数据集上的精确率优于ADV 和IBP,并且在所有攻击算法下的准确率也是最优的。在文本分类中,LSTM 比CNN 模型更容易受到对抗性攻击。在GA 算法的攻击下,ORIG、ADV、IBP 和RAN 训练的LSTM 准确率分别为0.2%、32.0%、64.3% 和35.5%,而TADT 训练的LSTM 准确率仍然可以达到82.9%。由于IMDB 中句子的平均长度为255 个单词,句子越长,对手可以对基于单词替换的扰动就越多。总地来说,TADT 在CLN 干净数据集上优于IBP,与ADV相当,并且在所有攻击方式下都优于其他防御方法。结果表明,本文TADT 方法具有更高的性能和更好的鲁棒性。 本文方法在TADTEXP中计算每个样本的对抗分布时,对每个样本分布的估计都需要进行k次采样,并进行T次梯度上升,这会耗费大量时间,使训练时间成倍增加,消耗大量的计算资源。本文在TADTEXP-GE中添加了一个VAE 网络,减少了上述的k次采样步骤,在相同条件下训练时间要少得多。一般来说,在给定相同的网络结构的情况下,使用TADTEXP增强模型鲁棒性的训练时间比TADTEXP-GE的训练时间慢4~5 倍。表3 所示为TADTEXP-GE训练方式的性能提升。可以看出,TADTEXP-GE效率明显提高。 表3 两种训练方式的性能提升 Table 3 Performance improvement of the two training methods 本节对TADT 进行消融实验,分析TADT 面对不同变化的稳健性和泛化性能。消融实验结果如表4所示,其中,w/o PRE 表示原始模型在对抗性攻击下的准确性,ADV 对抗训练算法的原始模型表示为w/o ADV-TRAIN,TADT 为使用本文方法进行训练的原始模型。 表4 消融实验结果 Table 4 Results of ablation experiment % 从表4 可以看出,由于没有使用对抗防御算法,在没有任何保护下,原始模型受影响最大。在相同的神经网络模型下,与TADT 相比,在PWWS、GA 和UAT 算法攻击下,w/o PRE 准确率分别下降了50.4%、63.2%和34.2%,w/o ADV-TRAIN 准确率分别下降了30.5%、43.7%和30.2%。 本文选择同义词替换攻击,主要是因为它是最有影响力和使用最广泛的文本对抗攻击方法之一。目前基于这种思路的攻击方法较多,例如HotFlip[37]、PWWS[32]、GA[36]、TextWitter[38]等。另外,本文还 针对基于梯度下降的攻击方法进行测试,证明该方法也是非常有效的。 本文基于文本分类任务提出一种基于分布式扰动的防御对抗攻击方法,能够在不牺牲性能的情况下大幅提高正确分类对抗样本的准确性。TADT 是一种用于文本对抗分布的方法,可在熵的正则化下描述自然样本周围的对抗样本。实验结果表明,使用对抗分布训练的分类模型在具有不同网络结构的数据集上优于其他对抗防御方法。下一步将对更多文本分类模型进行训练研究,将本文方法扩展到其他文本分类任务中。3.2 文本对抗分布训练
3.3 TADTEXP的通用算法
4 对抗训练时间复杂度的改善
5 实验

5.1 文本分类实验


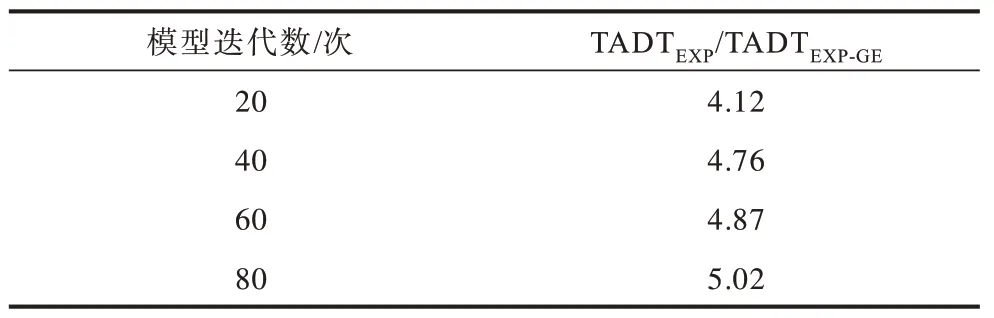
5.2 训练性能
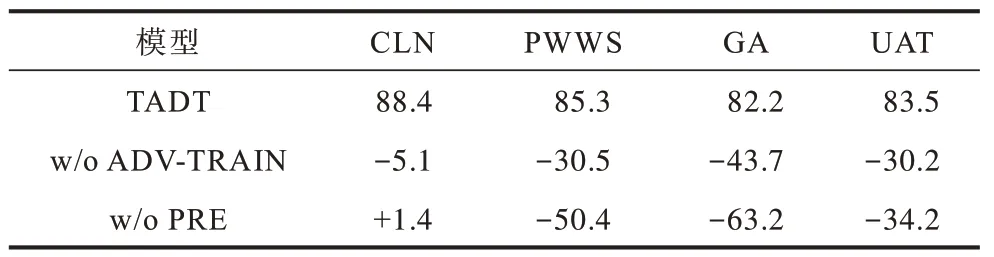
5.3 消融实验
6 结束语

