深度学习视域下的“问题串”设计的教学案例*——以“三角函数的概念”为例

广东广雅中学 (510160) 林才雄

长期以来,我们的教师勤勉而努力,但对于究竟如何在教学中实现对学生的核心素养的培养,实现立德树人的根本任务,却少有思考. 作为培养核心素养的重要途径、触及学生心灵的教学、教师充分发挥主导作用的活动,深度学习应运而生[1].

深度学习,它强调教师的引领作用,它是教学活动而不是一般学习者的自学活动,学生要学习比自身现有水平高得多、难得多的内容,还要以较短的时间、较快的速度去学习.

要突出教师的主导作用,使学生成为教学的主体,引发学生的深度学习,教师要做以下几件事: ①确定学生自觉发展的“最近发展区”; ②确定通过什么样的内容来提升、发展学生,即转化教学内容,提供恰当的“教学材料”; ③帮助学生“亲身”经历知识的发现与建构过程,使学生真正成为教学的主体[1].

下面,以高中数学新教材人教A 版第五章第二节“三角函数的概念”为例,给出深度学习视域下的“问题串”设计的教学案例.

1 情境引入

问题1-1在大型游乐场中,我们经常会看到一种大型转轮状机械建筑设施——摩天轮,乘客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色. 据了解,某摩天轮最高点距离地面168 米,转盘直径160 米,游客乘坐在座舱P,从距离地面最近的位置A处出发,转盘按照逆时针方向匀速旋转,旋转一周约30 分钟,请问在转动过程中,座舱P距离地面的高度h是时间t的函数吗? 为什么? 你能用学习过的函数来刻画吗?

生因为对于每一个确定的时间t(t＞0),都有唯一确定的一个高度h(8 ≤h≤168)和它对应,所以座舱P距离地面的高度h是时间t的函数. 因为每隔30 分钟,高度h的取值会重复出现,具有周期变化的规律,所以不能用学习过的函数来刻画.

设计意图三角函数作为本章节的核心概念, 问题1-1是本节的核心问题,围绕着大观念,突出大概念,串联学科知识,是渗透大观念、落实大概念的基本载体[2]. 摩天轮也是大多数学生生活中常见的事物,具有亲切感,但同时,问题1-1对只学习了一次、二次、幂、指、对数函数的学生来说,也是非常具有挑战性的一个问题,引发了学生的认知冲突,吸引学生作进一步的学习探究.

问题1-2我们发现座舱P的位置具有周期变化的规律,你认为这是由什么因素造成的?

生座舱P围绕转盘中心O做匀速圆周运动.

设计意图明确造成座舱P的位置具有周期变化规律的原因,为进一步简化研究问题,进行数学建模做铺垫,同时也发展学生的数学抽象、数学建模素养.

问题1-3如图,我们将问题简化为,单位圆O上的动点P从点A出发,按照逆时针方向做匀速圆周运动,借助平板上的ggb 几何画板,你认为可以用什么量来刻画点P的位置呢?

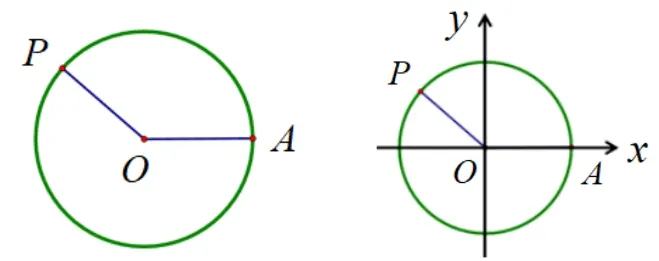
师为了方便,以点O为原点,以射线OA为x轴的非负半轴,建立平面直角坐标系xOy,其中,点A的坐标为(1,0).

生1设射线OA从x轴的非负半轴开始,绕点O按逆时针方向旋转角α,终边为OP,那么点P的位置可以用角α的终边与单位圆的交点来刻画.

生2点P的位置还可以用点P的坐标(x,y)来刻画.

师生1、生2 都说的很好,大家觉得用哪个量来刻画点P的位置更好呢?

生3我觉得用角α来刻画更好, 因为每隔2π的整数倍,角α的终边会呈现周而复始的变化规律,更能体现点P的位置的变化特点.

生4我觉得用坐标(x,y)来刻画更好,可以精确地告诉我们点P与x轴和y轴的距离.

师大家畅所欲言,表达了自己的观点,非常好.

设计意图学生通过亲自动手的活动体验,明确在平面直角坐标系中去刻画动点P的位置的两个关键要素——角α和坐标(x,y),自然而然引出了一类新的函数(三角函数)的学习.

2 新知探究

问题2-1当时,点P的坐标是什么? 当或时,点P的坐标又是什么? 一般地,任意给定一个角α∈R,它的终边OP与单位圆交点P的坐标(x,y)能唯一确定吗?

生当时, 点P的坐标是; 当时, 点P的坐标是(0,1); 当时, 点P的坐标是; 一般地,任意给定一个角α,它的终边OP是唯一确定的,它的终边OP与单位圆交点P的坐标(x,y)也是唯一确定的.

设计意图建立刻画点P的位置的两个要素之间的对应关系,为接下来生成三角函数的概念作准备.

问题2-2你认为点P的坐标(x,y)是角α的函数吗?如果是,你能用集合与对应语言来刻画这种函数关系吗?

生1函数是数集与数集之间的对应关系,虽然在弧度制下,任意给定一个角α,都可以用唯一确定的实数来表示,但坐标(x,y)对应的是一个点,不是一个数,所以不是函数.

师说的非常好,点的坐标是有序实数对,是两个数,不是一个数!

生2那它们不存在函数关系了吗? 纳闷了!

师显然点P的坐标(x,y)不是角α的函数,大家觉得谁才是角α的函数呢?

生3我知道了,点P的纵坐标y才是角α的函数,因为对于任意给定的一个角α∈R,都有唯一确定的点P的纵坐标y∈[-1,1]和它对应.

生4这样的话,点P的横坐标x也是角α的函数,因为对于任意给定的一个角α∈R,也都有唯一确定的点P的横坐标x∈[-1,1]和它对应.

师非常好,这些都是角α的函数,其实我们还可以找到很多角α的其他函数, 比如点P的纵坐标y与横坐标x(x̸= 0)的比值也是角α的函数,因为对于任意给定的一个角也都有唯一确定的比值和它对应.

设计意图回归函数的概念,明确函数概念的本质,即两个非空数集之间的“一对一”或“多对一”的对应关系,从一般到特殊,感受作为一类特殊的函数,三角函数并不神秘,它也具有函数的三要素.

3 概念生成

(板书)设角α是一个任意角,α∈R,它的终边OP与单位圆相交于点P(x,y).

(1)把点P的纵坐标y叫做α的正弦函数, 记作sinα,即y=sinα;

(2)把点P的横坐标x叫做α的余弦函数,记作cosα,即x=cosα;

(3)把点P的纵坐标与横坐标的比值叫做α的正切函数,记作tanα,即

我们把正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为: 正弦函数y= sinx,x∈R; 余弦函数y=cosx,x∈R;正切函数y=tanx,

4 概念辨析

问题3-1以正弦函数y= sinx,x∈R 为例,请说说三角函数与以往学习的函数的定义有什么不同?

生1三角函数是以角为自变量的一种函数,不同于以往学习的函数.

生2三角函数的对应法则比较特殊, 比如, 正弦函数y= sinx,x∈R,它的对应法则是角x的终边与单位圆的交点的纵坐标.

师是的, 三角函数是一类特殊的函数, 它以角为自变量,而且不同于以往学习的函数的对应法则,包括用解析式(代数运算)或列表或图象的形式给出的,它的对应法则可看作是一种几何操作的对应关系.

设计意图辨析三角函数的概念,明确其作为函数的三要素,同时,与以往学习的函数做对比,明确三角函数与以往学习的函数的异同点.

问题3-2在初中我们学了锐角三角函数,知道它们都是以锐角为自变量,以比值为函数值的函数. 那么本节定义的三角函数与初中定义的锐角三角函数之间有什么联系呢?

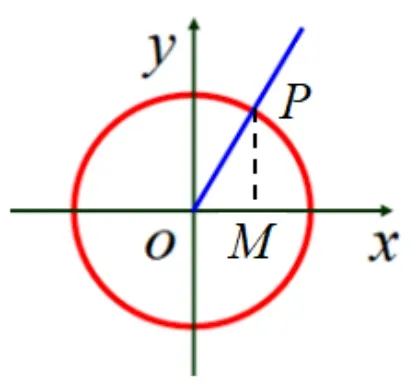
生如图, 设角的终边与单位圆交于点P(x,y),过点P作x轴的垂线PM于点M,则|PM| =y,|OM| =x, |OP| = 1, 根据初中所学的锐角三角函数的定义, 可知

这三个函数值与本节定义的结果相等,说明本节定义的三角函数与初中定义的锐角三角函数是一致的,同时本节的定义适用于任意角,它是对初中锐角三角函数概念的统一和拓展.

设计意图对比初中锐角三角函数与高中三角函数的概念,从特殊到一般,感受高中三角函数定义的统一性、优越性,从而对三角函数有了更高层次的认识与体会,在学生已有的经验与新知识之间建立意义关联,促进新知识的学习.

5 概念应用

问题4-1求角的正弦、余弦和正切值.

生在直角坐标系中, 作得到角的终边与单位圆的交点坐标所以

设计意图应用三角函数的定义,明确求解已知角的三角函数值的基本步骤,深化学生对三角函数的定义的理解.

问题4-2

(1) 已知角α的终边经过点, 求角α的正弦、余弦和正切值;

(2)已知角α的终边经过点P(-4,3),求角α的正弦、余弦和正切值;

(3)已知角α的终边经过点P(x,y),求角α的正弦、余弦和正切值;

(4)角α的各个三角函数值会随着终边上点P选取的改变而改变吗?

设计意图应用三角函数的定义求已知角的三角函数值,首先要确定角的终边与单位圆的交点坐标,然后才能根据定义,求出角的三个三角函数值. 而当已知角的终边上的任意一点的坐标时,根据三角形相似的原理,也可以得出所求角的三个三角函数值,而且所求值与终边上的点的位置无关,从而得到三角函数定义的推广形式,深化学生对三角函数概念的认识,以及用单位圆来定义三角函数的便捷性、优越性.

附三角函数定义的推广形式

设角α是一个任意角,P(x,y)是α终边上任意一点,点P与原点的距离

6 课堂总结与课后作业(略)

“问题串”设计的教学模式,是教师对教学内容的重新整合,对学习对象的深度加工,同时,学生通过问题串,有了自主的活动,并通过活动领会教学内容的内在意义,才有了以学生为主体的深度学习.

总的来说,“问题串”设计的教学模式是一种高效的教学方式,减轻了学生的学习负担,也让学生的自主学习能力得到了提升,符合新课程改革的要求[4]. 在教学实践中熟练地运用“问题串”设计教学,可以说为数学学科的深度学习提供了一种重要教学方式.