善用转化思想化解圆锥曲线中的运算难点*

广东省中山市桂山中学 (528463) 林娜

解析几何一直是高考重点考查的内容,也是一个难点内容,是高考的一块“硬骨头”. 解析几何问题的难主要体现在运算上,大部分学生在繁琐和复杂的运算中找不到运算的方向,丧失了信心,也丢掉了宝贵考试时间和分数. 其实运算的难很大一部分原因是我们没有找到合适的运算途径和方向,没有学会转化,如果我们能够善用转化思想,将复杂的陌生的问题转化为简单的熟悉的问题,我们就能够找到合适的运算途径和方向去化解圆锥曲线中的一些运算难点.

1 准备知识

以上结论是圆锥曲线中的常见二级结论,由于篇幅的限制,证明过程略,详细证明过程读者可查看参考文献.

接下来我们通过一些典型的例题来展示转化思想在化解圆锥曲线中的运算难点时所发挥的作用.

2 典型问题

2.1 转化为中点弦问题

点评本题的解决方法有很多(读者可自行研究),通常的做法是将面积的比例关系转化为坐标关系,然后经过变形可以用韦达定理将条件表达出来,最后将韦达定理代入,得出结论,中间的运算过程比较复杂,也需要花费较多时间. 经过转化后,我们看清楚了这道题所给条件的本质,本质就是PQ的中点与MN的中点重合,再结合直角三角形的性质和中点弦的结论,很容易得到正确答案.

2.2 转化为斜率之积为定值

2.3 转化为斜率之和为定值

2.4 转化为坐标之比

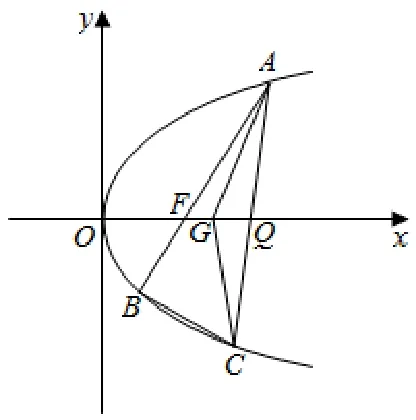
(2019 年浙江卷)如图,已知点F(1,0) 为抛物线y2=2px(p＞0) 的焦点, 过点F的直线交抛物线于A,B两点, 点C在抛物线上, 使得ΔABC的重心G在x轴上,直线AC交x轴于点Q,且Q在点F右侧. 记ΔAFG,ΔCQG的面积为S1,S2.

2.5 转化为向量的数量积

3 巩固练习

4 教学反思

带领学生阅读相关文献资料,证明储备知识的结论,再把相关的转化思想应用于不同的题目,在课堂中很好的实现了文献阅读与写作的数学教学内容,让学生通过文献阅读实现举一反三,授之以鱼,不如授之以渔. 今后也可提供给学生优秀的阅读材料,让学生去写阅读启示,以及同类问题的解决方法等. 仅以本文给学生以示范,本课例应该作为单元教学设计,设计3 或4 个课时去完成,这节课为学生碰到新的圆锥曲线问题提供了方法上的指引,以至于不再畏惧冗长复杂的各种圆锥曲线第二问.