数学核心素养测评之小学数学核心素养分析

胡典顺 王慧鋆

胡典顺

华中师范大学数学与统计学学院教授、博士研究生导师，华中师范大学数学教育教研室主任，湖北省中学数学教学指导委员会副主任委员；《数学教育学报》《数学通讯》编委，鄂教版高中数学教材（2019年版）副主编，中国国际文化交流基金会第三届“明德教师奖”获得者；曾以访问学者的身份，由国家留学基金委公派访问美国特拉华大学；在《课程·教材·教法》《中国教育学刊》《数学教育学报》《教育科学研究》等期刊上发表论文270余篇，出版《基于数学意义的数学教学改革研究》《整合技术的学科教学知识：从教师专业素养到教师教学实践》《中学生数学素养测评的模型建构与实证研究》等专著，主持多项全国教育科学规划项目和教育部人文社会科学研究规划基金项目。

数学核心素养测评主要围绕内容领域、情境领域、过程领域、核心素养领域四个维度进行。其中，核心素养领域的测评体现在其他三个领域测评之中，是成绩分析的核心内容。由于小学和初中两阶段的数学核心素养的主要表现不同，試题测评内容也有所不同。本文基于“WJ市义务教育核心素养监测”的核心素养领域部分，介绍小学阶段试题的核心素养表现，以及测评数据的分析过程和结果。

一、核心素养在试题中的表现

数学核心素养测评的目标包括立体、综合地呈现学生的数学核心素养现状，探究影响学生数学核心素养发展的因素，为培育学生的数学核心素养提供教学建议。为实现这一目标，试题编制要注重紧密结合数学知识和数学素养，让整套试卷涵盖课程标准指出的小学阶段的所有核心素养。

根据《义务教育数学课程标准（2022年版）》，小学阶段的数学核心素养主要表现为数感、量感、符号意识、运算能力、几何直观等11个方面。命题人编制试题时，既要使一道题可以考查多个知识点、涉及多个核心素养，又要根据每道题考查的最主要、最重要的知识点，将它的考查范围划入11个核心素养中的2个，以控制考查不同核心素养的题目占比，便于分析学生的不同核心素养表现。经过对课标、教材等的分析，命题人将各个数学核心素养在整套试卷的分值占比分配如下：运算能力为24.0%，推理意识为13.5%，创新意识为11%，数感为9%，数据意识为7%，应用意识、量感均为6.5%，符号意识、几何直观、空间观念均为6%，模型意识为4.5%。从整体上看，整套试卷着重考查学生的运算能力和抽象能力，且突出创新意识核心素养的考查，符合学生的认知发展情况，能较好地测评四年级学生的数学核心素养水平。

在确定素养考查比例的基础上，命题人整理了核心素养在具体试题中的考查情况。受篇幅限制，笔者只列出其中3道试题的考查情况（如表1所示）。

下面，笔者以“七巧板”问题为例，介绍题目是如何考查核心素养的。

七巧板又称七巧图、智慧板，由七块板组成，是我国民间流传下来的智力玩具。它由宋代的宴几演变而来，原为文人玩的一种室内游戏，后在民间演变为拼图玩具。为便于区分，我们把这七块板标上号码（如图1）。

问题1  图1中，1～7号板中共有________个三角形，________个四边形。

问题2  下面是有关图1的叙述。这些叙述正确吗？请对每个叙述涂选“是”或“否”。

问题3  图2展示的是用1～6号板拼成的一个轴对称图形，请你把剩下的7号板画在图2的合适位置，使这七块板组成的仍然是一个轴对称图形。

该案例是四年级学生数学核心素养测评试题之一，考查学生对几何图形的认识与测量，以及图形变换等知识。其中，问题1考查学生对三角形、四边形等的认识，涉及数感、几何直观两个核心素养；问题2考查角的大小、图形变换、正方形面积公式等知识，涉及运算能力、空间观念两个核心素养；问题3是一道开放性试题，考查学生对轴对称图形的认识与理解，涉及推理意识、创新意识两个核心素养。总体来看，三个问题形式不同、各有侧重，一共考查了6个核心素养，比较全面。

二、测评分析过程及结果

得到测评数据后，笔者这样分析：先进行描述性统计，了解分值、得分率等一般情况；接着从“三会”视角进行整体分析，了解学生的核心素养发展水平及分布情况；然后通过相关性分析，定量研究各个核心素养测试结果之间的内在联系；最后通过差异性分析，了解背景信息对学生核心素养发展水平的影响。

1.核心素养测评结果统计

基于“WJ市义务教育核心素养监测”项目收集到的3544份有效数据，笔者借助SPSS26.0统计得出：参加测试学生得分的最大值是100分（满分），最小值是1分，均值是66.3分，说明学生成绩良好，平均水平较高；标准差是16.5分，说明现阶段学生核心素养水平差异较大。

在具体的核心素养表现得分上，11个核心素养的均分、得分率等分布情况如图3所示。

由图3可知，学生在几何直观、空间观念两个核心素养上得分率最高，均在85%以上；在数感、量感等核心素养上得分率较高，均在75%以上；在运算能力上得分率次高，为63.5%；在推理意识、应用意识上得分率一般，未到60%；在模型意识上得分率最低，为47.2%。这一方面说明学生在几何直观、空间观念、数感、量感等核心素养上表现良好，另一方面说明学生的数学知识运用能力一般，后续学习中要加强。

2.“三会”视角下的核心素养分析

新课标提出了“三会”，使我们从更高层面看待数学核心素养。小学阶段的数学核心素养可以根据“三会”分为三个类别：“会用数学的眼光观察现实世界”包括数感、量感、符号意识、几何直观、空间观念和创新意识，“会用数学的思维思考现实世界”包括运算能力和推理意识，“会用数学的语言表达现实世界”包括数据意识、模型意识和应用意识。“三会”将数学眼光、数学思维、数学语言融为一体，是学生数学能力、数学思维品质和情感、态度与价值观的综合体现。下面，笔者从“三会”出发，整体分析数学核心素养测评数据。

为清晰地刻画学生数学核心素养的发展水平，本文采用PISA测试所使用的精熟度水平划分方法描绘当下学生数学核心素养所处的层次。由于不同核心素养在整套试卷中的分值占比不同，为方便比较分析，笔者先将学生的成绩加权成100分，再进行水平划分。基于3544份有效数据，笔者计算得出如表2所示的精熟度水平等级分布。

为更好地呈现学生成绩在“三会”视角下的精熟度水平分布，笔者绘制精熟度水平分布百分比条形图，如图4所示。

由图4可知，在数学眼光上，精熟度水平为5级的学生比例最高，接近25%；在数学思维上，精熟度水平为3级的学生比例最高，为20.5%；在数学语言上，精熟度水平为3级的学生比例最高，为20.1%。此外，“三会”精熟度水平在5级及以上的学生占比都超过30%，在2级及以上的学生占比都超过85%，表明被试中有相当一部分学生的精熟度水平是高水平，并且大部分学生数学基础较好，数学核心素养表现良好。

为了解“三会”视角下不同水平学生占比的变化趋势，笔者绘制相应的折线图，如图5所示。

由图5可知，从数学眼光到数学思维再到数学语言，0级、1级精熟度水平的学生占比越来越高，5级、6级精熟度水平的学生占比越来越低。这说明随着所考查核心素养难度的提升，学生在推理、模型等方面的素养表现逐步变弱。这在预期之中，我们相信随着学段的提升和教师对学生思维能力的不断培养，在推理、模型等核心素养上表現出高水平的学生占比会越来越高。

3.核心素养相关性分析

用统计分析方法定量研究学生在不同核心素养方面的成绩相关性及相关程度，能让我们更加清楚地看到核心素养之间的联系，明确素养培育的方向。

笔者利用SPSS26.0对学生在数学眼光、数学思维、数学语言上的成绩进行皮尔逊相关性分析，结果如表3所示。

表3显示，数学眼光与数学思维的皮尔逊相关系数约为0.748，数学眼光与数学语言的皮尔逊相关系数约为0.725，数学思维与数学语言的皮尔逊相关系数约为0.825。这表明三者之间两两正相关，且在0.01的统计水平上显著相关。其中，数学思维与数学语言的相关系数最大，相关程度最高，说明第二学段学生的数学思维与数学语言联系更密切。总的来看，以“三会”划分的数学核心素养类别之间彼此联系、相互影响，教师要在教学中注重核心素养之间的联系，根据教学内容有针对性地培育学生的核心素养，促进学生核心素养的协调发展。

4.差异性分析

差异性分析可以帮助我们了解背景信息对学生核心素养发展水平的影响。调查问卷中的一些信息，如学生所在区（县）、学校的办学类型以及学生性别等，都可以作为差异性分析对象。

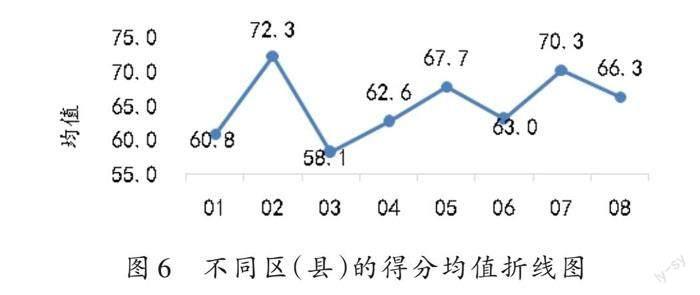
笔者用01～07表示7个区（县）、08表示全市，借助SPSS26.0得出各区（县）的学生核心素养表现均值，并绘制如图6所示的折线图。

由图6可知，全市数学核心素养的得分均值为66.3分（满分100分），其中02、05、07这三个区（县）的得分均值在总均值之上，其他区（县）的得分均值都低于总均值，02地区学生的得分均值最高，数学核心素养表现最好。可见，不同区（县）学生的数学核心素养发展水平存在一定的差异。

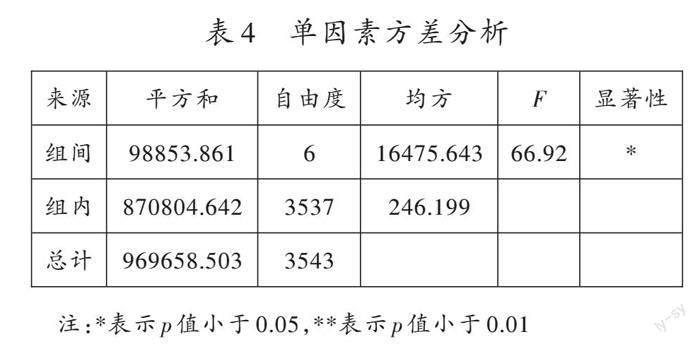
为确定各区（县）的均值差异是否显著，笔者在0.05的统计水平上作单因素方差分析，结果如表4所示。

由表4可知，组间F值为66.92，显著性p值小于0.05，拒绝原假设，表明不同区（县）学生的得分均值存在显著性差异。

三、结语

我们通过试题监测学生的数学核心素养表现，再通过数据分析反馈、评价学生的核心素养水平，能在一定程度上把握学生的数学核心素养现状，明晰影响数学核心素养发展的相关因素。数学核心素养是在数学学习过程中逐渐形成和发展的，不同学段学生的发展水平不同，学生现阶段的核心素养水平并不能代表他们未来的核心素养水平，所以学生数学核心素养水平的监测、分析需长期进行。在条件允许的情况下，我们可以关联学生的数学核心素养表现与日常学习情况，对学生进行跟踪测评，并将测评数据和结果录入成长档案中。这样做更能全面地把握学生的数学核心素养发展情况，总结学生数学核心素养发展规律。

（王慧鋆系华中师范大学数学与统计学学院硕士研究生）

责任编辑  刘佳